数据结构(六)——图
六、图
6.1 图的基本概念
图的定义
图:图G由顶点集V和边集E组成,记为G = (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V = {v1, v2, … , vn},则用|V|表示图G中顶点的个 数,也称图G的阶,,用|E|表示图G中边的条数。
注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
无向图:若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v, w)或(w, v),因为(v, w) = (w, v),其 中v、w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w) 依附于顶点w和v,或者说边(v, w)和顶点v、w相关联
有向图:若E是有向边(也称弧)的有限集合时,则图G为有向图。 弧是顶点的有序对,记为<v,w>,其中v、w是顶点,v称为弧尾,w称为弧头,<v,w>称为从顶点v到顶点w的弧,也称 v邻接到w,或w邻接自v。<v,w> ≠<w,v>

简单图——① 不存在重复边; ② 不存在顶点到自身的边 (数据结构课程只探讨 “简单图”)
多重图——图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联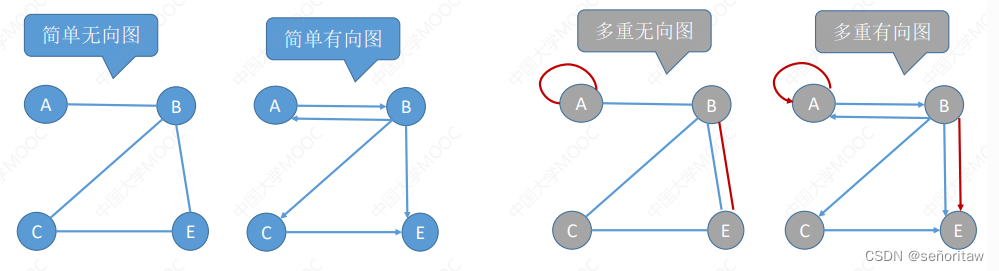
顶点的度、入度、出度
无向图:顶点v的度是指依附于该顶点的边的条数,记为TD(v)。
在具有n个顶点、e条边的无向图中,![]() 即无向图的全部顶点的度的和等于边数的2倍
即无向图的全部顶点的度的和等于边数的2倍
有向图:入度是以顶点v为终点的有向边的数目,记为ID(v);
出度是以顶点v为起点的有向边的数目,记为OD(v)。
顶点v的度等于其入度和出度之和,即TD(v) = ID(v) + OD(v)。
在具有n个顶点、e条边的有向图中,![]() ,即入度和出度的数量相等且等于e
,即入度和出度的数量相等且等于e
顶点的关系描述
路径——顶点vp到顶点vq之间的一条路径是指顶点序列,![]()
回路——第一个顶点和最后一个顶点相同的路径称为回路或环
简单路径——在路径序列中,顶点不重复出现的路径称为简单路径。
简单回路——除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
路径长度——路径上边的数目
点到点的距离——从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离。 若从u到v根本不存在路径,则记该距离为无穷(∞)。
无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是强连通的
图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。
若图中任何一对顶点都是强连通的,则称此图为强连通图。
研究图的局部—子图、生成子图
设有两个图G = (V, E)和G ′ = (V ′ , E ′ ),若V ′ 是V的子集,且 E ′ 是 E的子集,则称G ′ 是G的子图
若有满足V(G ′ ) = V(G)的子图G ′ ,则称其为G的生成子图
有向图的子图和生成子图也是一样的
无向图中的极大连通子图称为连通分量
子图必须连通,且包含尽可能多的顶点和边
有向图中的极大强连通子图称为有向图的强连通分量
子图必须强连通,同时 保留尽可能多的边
生成树:连通图的生成树是包含图中全部顶点的一个极小连通子图。
若图中顶点数为n,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通 图,若加上一条边则会形成一个回路。(因此边要尽可能的少,但要保持连通)
生成森林:在非连通图中,连通分量的生成树构成了非连通图的生成森林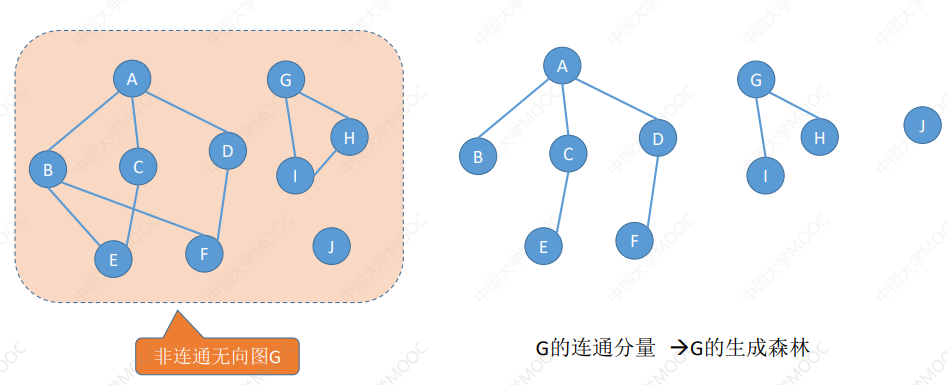
边的权、带权图/网
边的权——在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。
带权图/网——边上带有权值的图称为带权图,也称网。
带权路径长度——当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
特殊形态的图
无向完全图——无向图中任意两个顶点之间都存在边
若无向图的顶点数|V|=n,则
有向完全图——有向图中任意两个顶点 之间都存在方向相反的两条弧
若有向图的顶点数|V|=n,则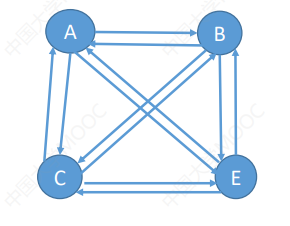
稀疏图:边数很少的图称为稀疏图 反之称为稠密图
树——不存在回路,且连通的无向图
n个顶点的树,必有n-1条边。
常见考点:n个顶点的图,若 |E|>n-1,则一定有回路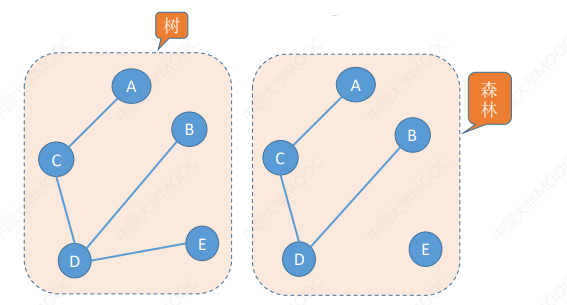
有向树——一个顶点的入度为0、其余顶点的 入度均为1的有向图,称为有向树

相关文章:

数据结构(六)——图
六、图 6.1 图的基本概念 图的定义 图:图G由顶点集V和边集E组成,记为G (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V {v1, v2, … , vn},则用|V|…...

Android-AR眼镜屏幕显示
Android-AR眼镜 前提:Android手持设备 需要具备DP高清口 1、创建Presentation(双屏异显) public class MyPresentation extends Presentation {private PreviewSingleBinding binding;private ScanActivity activity;public MyPresentatio…...

蓝桥集训之货币系统
蓝桥集训之货币系统 核心思想:背包 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N 30,M 10010;typedef long long LL;LL f[M];int w[N];int n,m;int main(){cin>>n>>m;for(int i1;i&…...

基于微信小程序的校园服务平台设计与实现(程序+论文)
本文以校园服务平台为研究对象,首先分析了当前校园服务平台的研究现状,阐述了本系统设计的意义和背景,运用微信小程序开发工具和云开发技术,研究和设计了一个校园服务平台,以满足学生在校园生活中的多样化需求。通过引…...
QT+Opencv+yolov5实现监测
功能说明:使用QTOpencvyolov5实现监测 仓库链接:https://gitee.com/wangyoujie11/qt_yolov5.git git本仓库到本地 一、环境配置 1.opencv配置 将OpenCV-MinGW-Build-OpenCV-4.5.2-x64文件夹放在自己的一个目录下,如我的路径: …...

【Python-Docx库】Word与Python的完美结合
【Python-Docx库】Word与Python的完美结合 今天给大家分享Python处理Word的第三方库:Python-Docx。 什么是Python-Docx? Python-Docx是用于创建和更新Microsoft Word(.docx)文件的Python库。 日常需要经常处理Word文档…...
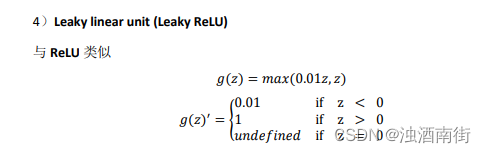
吴恩达深度学习笔记:浅层神经网络(Shallow neural networks)3.6-3.8
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第三周:浅层神经网络(Shallow neural networks)3.6 激活函数(Activation functions)3.7 为什么需要非线性激活函数?(why need a non…...

盘点最适合做剧场版的国漫,最后一部有望成为巅峰
最近《完美世界》动画官宣首部剧场版,主要讲述石昊和火灵儿的故事。这个消息一出,引发了很多漫迷的讨论,其实现在已经有好几部国漫做过剧场版,还有是观众一致希望未来会出剧场版的。那么究竟是哪些国漫呢,下面就一起来…...

Altium Designer许可需求分析
在电子设计的世界中,Altium Designer已成为设计师们的得力助手。然而,如何进行有效的许可需求分析,以确保软件的高效使用和企业的可持续发展?本文将带您了解如何进行Altium Designer的许可需求分析,让您在设计的道路上…...

[c++]类和对象常见题目详解
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...
【c++】类和对象(五)赋值运算符重载
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好,本篇文章带大家认识赋值运算符重载,const成员,取地址及const取地址操作符重载等内容 目录 1.赋值运算符重载1.1运算符重载1.1.1特性&#…...
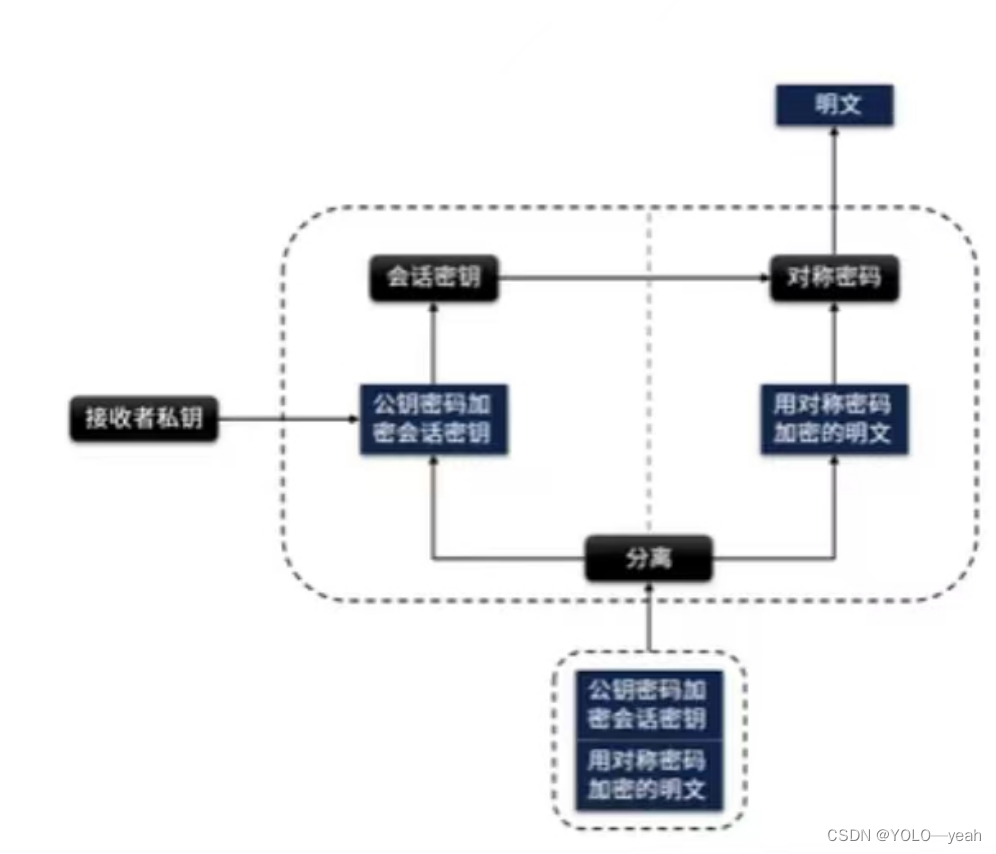
密码学基础-对称密码/公钥密码/混合密码系统 详解
密码学基础-对称密码/公钥密码 加解密说明1.加密解密必要因素加密安全性说明 什么是对称密码图示说明对称密码详解什么是DES?举例说明 什么是3DES什么是AES? 公钥密码什么是RSA? 对称密钥和公钥密码优缺点对比对称密码对称密码算法总结对称密码存在的问题? 公钥密码公钥密码…...
》)
《装饰器模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 模式说明: 方案: 装饰类和派生类同根,然后装饰类中放一个派生类,以在接口不动的情况下增加功能优点: 可以灵活地扩展对象功能…...

Spring Boot 整合分布式搜索引擎 Elastic Search 实现 自动补全功能
文章目录 ⛄引言一、分词器⛅拼音分词器⚡自定义分词器 二、自动补全查询三、自动补全⌚业务需求⏰实现酒店搜索自动补全 四、效果图⛵小结 ⛄引言 本文参考黑马 分布式Elastic search Elasticsearch是一款非常强大的开源搜索引擎,具备非常多强大功能,…...
实现一个Google身份验证代替短信验证
最近才知道公司还在做国外的业务,要实现一个登陆辅助验证系统。咱们国内是用手机短信做验证,当然 这个google身份验证只是一个辅助验证登陆方式。看一下演示 看到了嘛。 手机下载一个谷歌身份验证器就可以 。 谷歌身份验证器,我本身是一个基…...

Spring框架与Spring Boot的区别和联系
引言 Spring框架和Spring Boot都是Java生态中最受欢迎的开源框架,它们各自扮演着不同的角色,帮助开发者构建高效的企业级应用。本教程将从零基础的角度出发,让你轻松理解这两者的区别和联系。 Spring框架简介 Spring框架,简称Spri…...

[OpenCV学习笔记]Qt+OpenCV实现图像灰度反转、对数变换和伽马变换
目录 1、介绍1.1 灰度反转1.2 图像对数变换1.3 图像伽马变换 2、效果图3、代码实现4、源码展示 1、介绍 1.1 灰度反转 灰度反转是一种线性变换,是将某个范围的灰度值映射到另一个范围内,一般是通过灰度的对调,突出想要查看的灰度区间。 S …...

【大数据】Flink学习笔记
文章目录 认识FlinkDocker安装Flink基本概念Flink的特点Flink 和 Spark Streaming 对比 基本使用WordCount实现依赖 批模式代码流模式代码网络流模式代码在web UI上提交代码创建项目[^1]编写代码配置打包在Web UI上提交 Flink 架构系统架构核心概念并行度算子链(Opeartor Chain…...

社交网络的未来:Facebook如何塑造数字社交的下一章
引言 社交网络已成为我们生活中不可或缺的一部分,而Facebook作为其领军者,一直在塑造着数字社交的未来。本文将深入探讨Facebook在未来如何塑造数字社交的下一章,并对社交网络的发展趋势进行展望和分析。 1. 引领虚拟社交的潮流 Facebook将…...
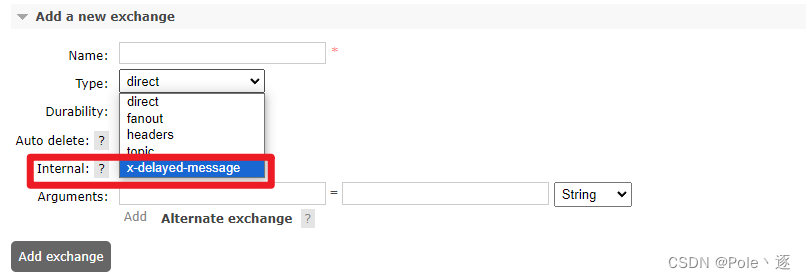
RabbitMQ 延时消息实现
1. 实现方式 1. 设置队列过期时间:延迟队列消息过期 死信队列,所有消息过期时间一致 2. 设置消息的过期时间:此种方式下有缺陷,MQ只会判断队列第一条消息是否过期,会导致消息的阻塞需要额外安装 rabbitmq_delayed_me…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

MAZANOKE结合内网穿透技术实现跨地域图像优化服务的远程访问过程
文章目录 前言1. 关于MAZANOKE2. Docker部署3. 简单使用MAZANOKE4. 安装cpolar内网穿透5. 配置公网地址6. 配置固定公网地址总结 前言 在数字世界高速发展的今天,您是否察觉到那些静默增长的视觉数据正在悄然蚕食存储空间?随着影像记录成为日常习惯&…...

《开篇:课程目录》
大家好!我是一名.NET技术开发者,长期以来积累了比较多的项目实战经验,现在把它分享给大家,希望能够帮助到大家,同时为.NET社区提供一份力量,让更多的开发者参与进来。 要讲解的课程如下: 《介绍…...
