第九届蓝桥杯大赛个人赛省赛(软件类)真题C 语言 A 组-分数

solution1
直观上的分数处理
#include <iostream>
using namespace std;
int main()
{printf("1048575/524288");return 0;
}
#include<stdio.h>
#include<math.h>
typedef long long ll;
struct fraction{ll up, down;
};
ll gcd(ll a, ll b){if(!b) return a;return gcd(b, a % b);
}
fraction r(fraction f){if(gcd(f.down, f.up) > 1){f.down /= gcd(f.down, f.up);f.up /= gcd(f.down, f.up);}return f;
}
fraction add(fraction f1, fraction f2){fraction f;f.down = f1.down * f2.down;f.up = f1.up * f2.down + f2.up * f1.down;return r(f);
}
int main(){fraction f, t;f.up = f.down = 1;for(ll i = 2; i <= pow(2, 19); i *= 2){t.up = 1;t.down = i;printf("%lld %lld\n", t.down, f.up);f = add(f, t);}printf("%lld %lld, %lld %lld", f.up / f.down, f.up % f.down, f.up, f.down);return 0;
}
solution2
手动通分计算为
(219+218+217……+20)/219= (220-1)/219
- 20+21+22+……+2n-1 = 2n-1
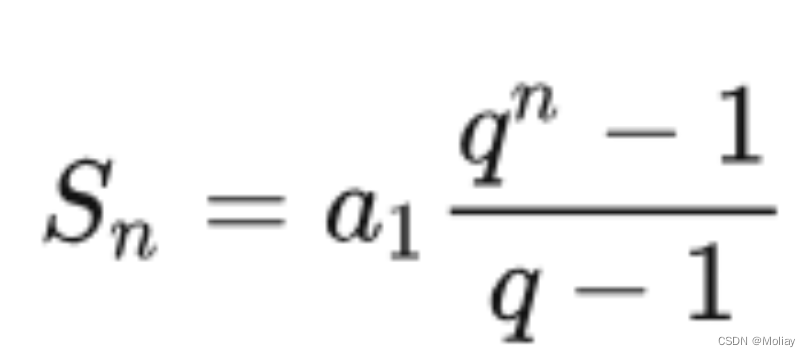
- 较大的数若比 较小的数 的两倍大于或者小1,则两者互质
#include<stdio.h>
#include<math.h>
typedef long long ll;
int main(){printf("%lld/%lld", (ll) pow(2, 20) - 1, (ll) pow(2, 19));//注意别漏了强转double -> llreturn 0;
}
相关文章:
第九届蓝桥杯大赛个人赛省赛(软件类)真题C 语言 A 组-分数
solution1 直观上的分数处理 #include <iostream> using namespace std; int main() {printf("1048575/524288");return 0; }#include<stdio.h> #include<math.h> typedef long long ll; struct fraction{ll up, down; }; ll gcd(ll a, ll b){if…...

并发编程——4.线程池
这篇文章我们来讲一下线程池的相关内容 目录 1.什么是线程池 1.1为什么要用线程池 1.2线程池的优势 2.线程池的使用 3.线程池的关闭 4.线程池中的execute和submit方法的一些区别 5.线程池的参数和原理 6.自定义线程池 7.总结 1.什么是线程池 1.1为什么要用线程池 首…...
阿里云魔搭发起“ModelScope-Sora开源计划”,将为中国类Sora模型开发提供一站式工具链
在2024年3月23日的全球开发者先锋大会上,阿里云的魔搭社区宣布了一个新计划:“ModelScope-Sora开源计划”。这个计划旨在通过开源方式,帮助中国在Sora模型类型上做出更多创新。这个计划提供了一整套工具,包括处理数据的工具、多模…...

大模型与数据分析:探索Text-to-SQL
当今大模型如此火热,作为一名数据同学,持续在关注LLM是如何应用在数据分析中的,也关注到很多公司推出了AI数智助手的产品,比如火山引擎数智平台VeDI—AI助手、 Kyligence Copilot AI数智助理、ThoughtSpot等,通过接入人…...

Unity VisionOS开发流程
Unity开发环境 Unity Pro, Unity Enterprise and Unity Industry 国际版 Mac Unity Editor(Apple silicon) visionOS Build Support (experimental) 实验版 Unity 2022.3.11f1 NOTE: 国际版与国服版Pro账通用,需要激活Pro的许可证。官方模板v0.6.2,非Pro版本会打…...

聊聊k8s服务发现的优缺点
序 本文主要研究一下使用k8s服务发现的优缺点 spring cloud vs kubernetes 这里有张spring cloud与kubernetes的对比,如果将微服务部署到kubernetes上面,二者有不少功能是重复的,可否精简。 这里主要是讲述一下如果不使用独立的服务发现&am…...

Tomcat是如何处理并发请求的?
Tomcat处理请求流程: Tomcat是采用了扩展JDK线程池的方案 :先启动若干数量的线程,并让这些线程都处于睡眠状态,当客户端有一个新请求时,就会唤醒线程池中的某一个睡眠线程,让它来处理客户端的这个请求,当处…...
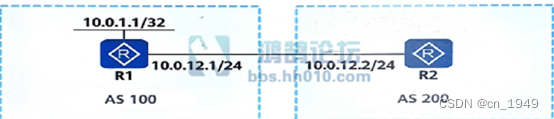
H12-831_561
单选题561、如图所示,R1使用Loopback0接口(IP地址为10.0.1.1/32)与R2的物理接口(IP地址为10.0.12.2/24)建立EBGP邻居关系,以下描述中正确的是哪一项? A.无需在R1和R2的BGP进程下指定ebgp-max-hop B.在R2的BGP进程下配置peer 10.0.1.1 ebgp-max-hop 2,且…...
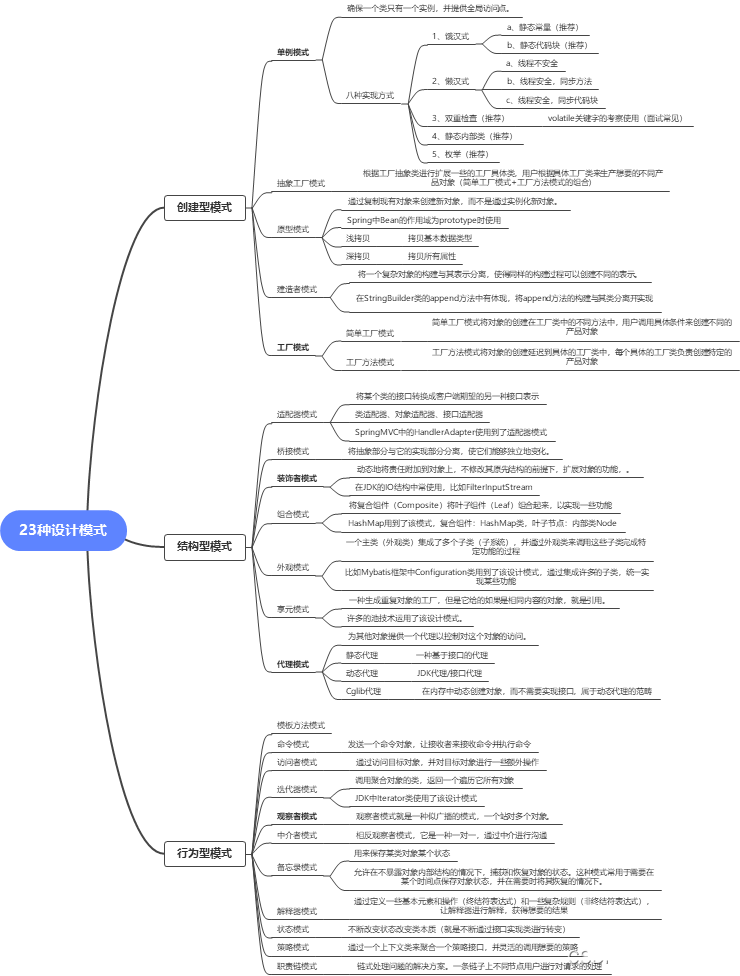
Java23种常见设计模式汇总
七大原则网站地址:设计模式7大原则+类图关系-CSDN博客 创建型设计模式:创建型设计模式合集-CSDN博客 七大结构型设计模式:7大结构型设计模式-CSDN博客 11种行为型设计模式: 11种行为型模式(上࿰…...
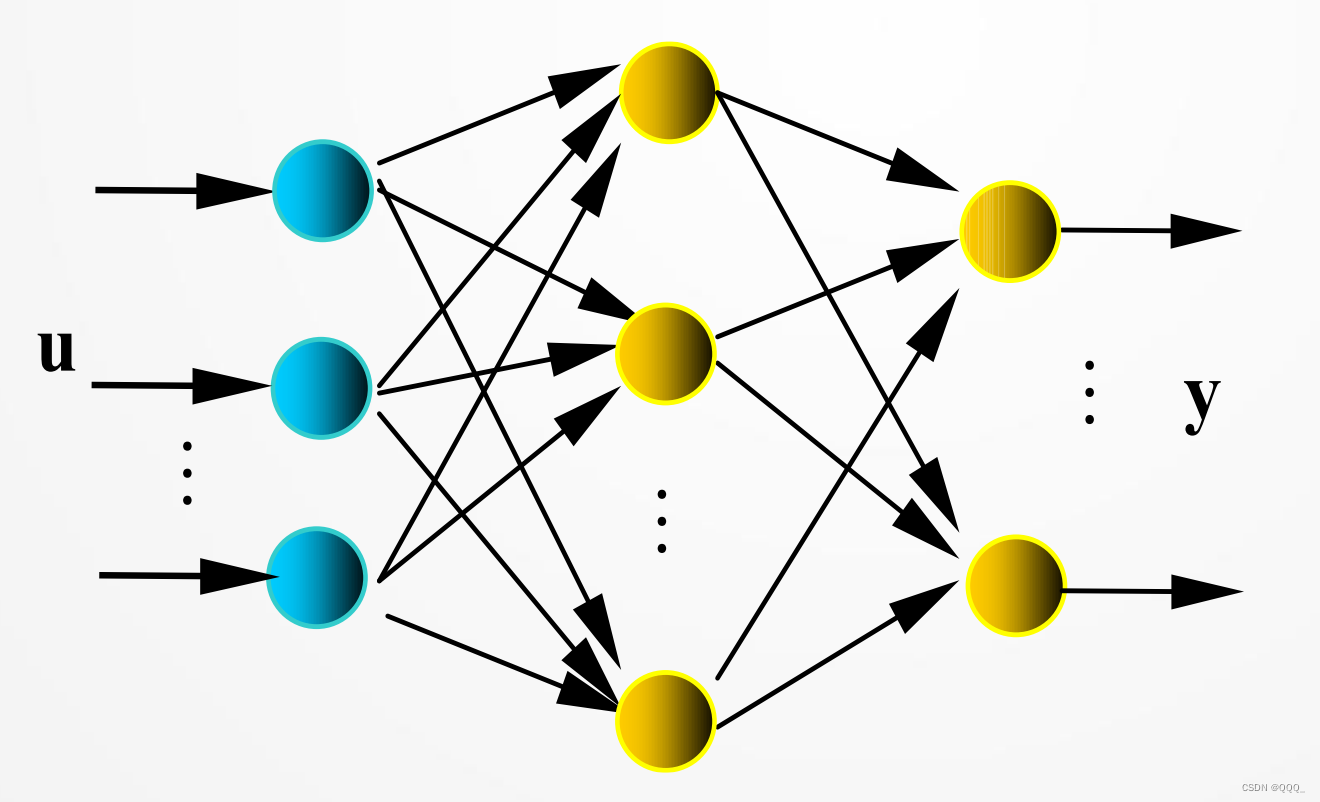
神经网络与深度学习(一)
线性回归 定义 利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法 要素 训练集(训练数据)输出数据拟合函数数据条目数 场景 预测价格(房屋、股票等)、预测住院时间&#…...
算法学习——LeetCode力扣图论篇2
算法学习——LeetCode力扣图论篇2 1020. 飞地的数量 1020. 飞地的数量 - 力扣(LeetCode) 描述 给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。 一次 移动 是指从一个陆地单元格走到另一个相…...
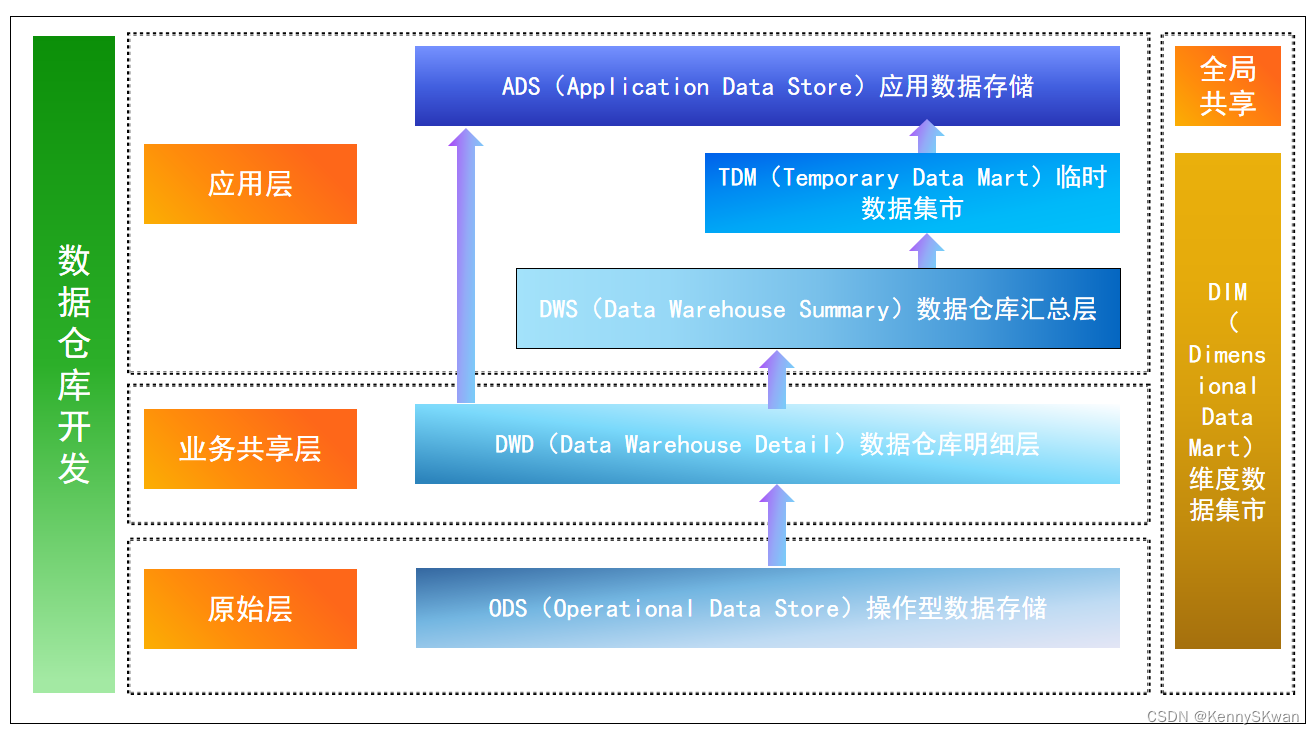
大数据设计为何要分层,行业常规设计会有几层数据
大数据设计通常采用分层结构的原因是为了提高数据管理的效率、降低系统复杂度、增强数据质量和可维护性。这种分层结构能够将数据按照不同的处理和应用需求进行分类和管理,从而更好地满足不同层次的数据处理和分析需求。行业常规设计中,数据通常按照以下…...

css3之2D转换transform
2D转换transform 一.移动(translate)(中间用,隔开)二.旋转(rotate)(有单位deg)1.概念2.注意点3.转换中心点(transform-origin)(中间用空格)4.一些例子(css三角和旋转) 三…...

pytest中文使用文档----6临时目录和文件
1. 相关的fixture 1.1. tmp_path1.2. tmp_path_factory1.3. tmpdir1.4. tmpdir_factory1.5. 区别 2. 默认的基本临时目录 1. 相关的fixture 1.1. tmp_path tmp_path是一个用例级别的fixture,其作用是返回一个唯一的临时目录对象(pathlib.Path…...
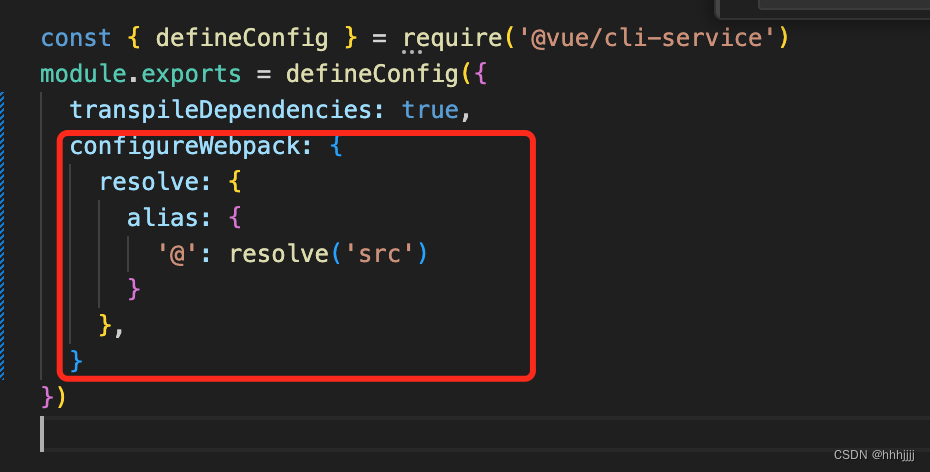
从0开始搭建基于VUE的前端项目
准备与版本 安装nodejs(v20.11.1)安装vue脚手架(vue/cli 5.0.8) ,参考(https://cli.vuejs.org/zh/)vue版本(2.7.16),vue2的最后一个版本 初始化项目 创建一个git项目(可以去gitee/github上创建ÿ…...
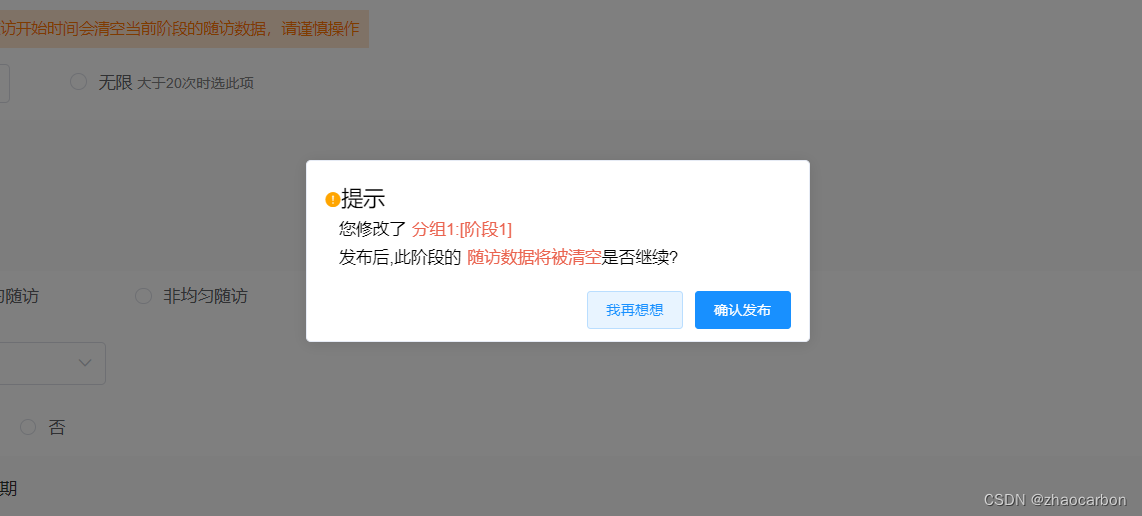
elementUI this.$msgbox msgBox自定义 样式自定义 富文本
看这个效果是不是很炫?突出重点提示内容,对于用户交互相当的棒! 下来说说具体实现: let self = this const h = self.$createElement; this.$msgbox({title: null,message: h("p", {style: "margin-top:10px"}, [h("i", {class: "el-i…...

Lua与Python区别
Lua和Python都是流行的编程语言,但它们在设计哲学、应用领域和性能特点上有所不同。以下是Lua和Python之间的对比: 1. **设计哲学**: - Lua被设计为一个轻量级的嵌入式脚本语言,重点在于简单性和效率。它有一个小巧的标准库,通…...
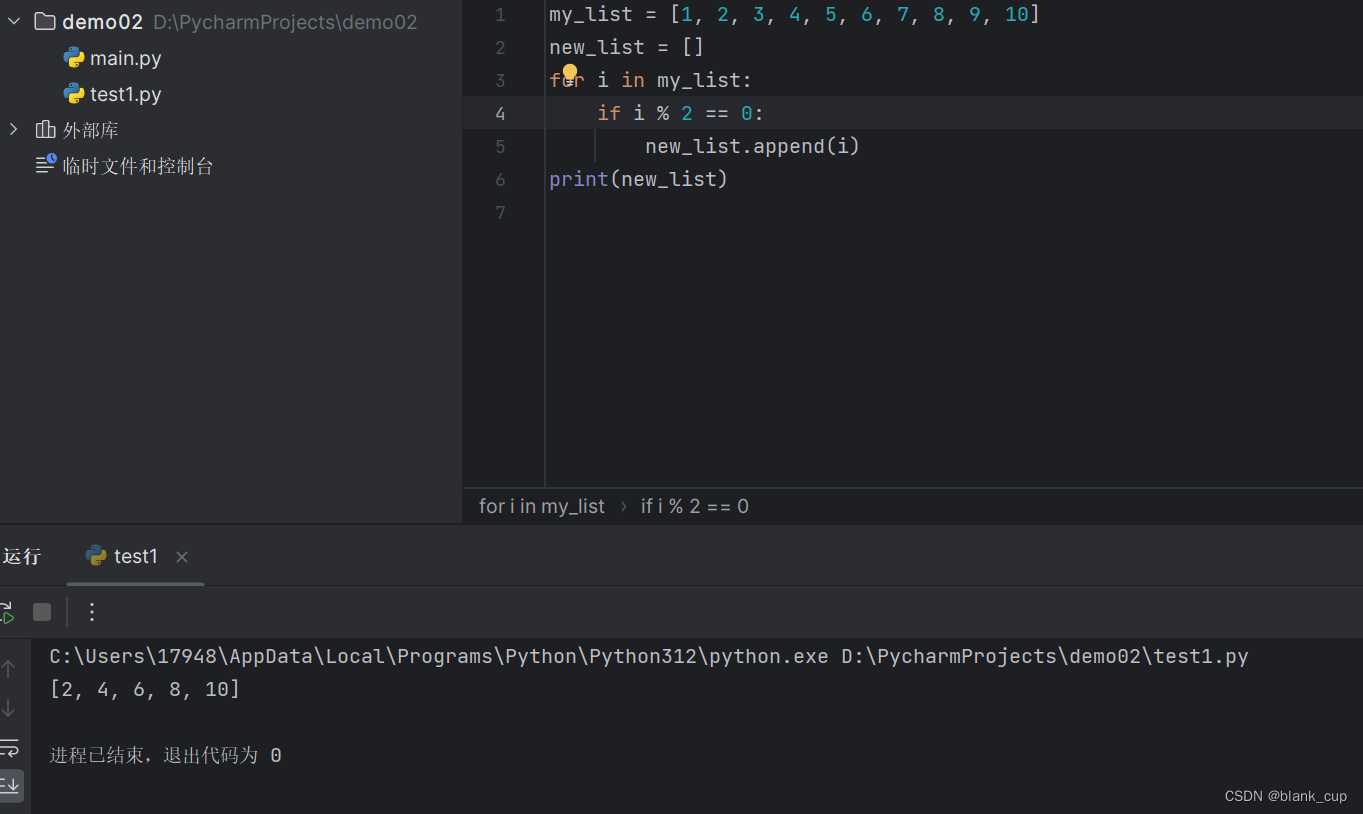
Python学习(二)
数据容器 数据容器根据特点的不同,如: 是否支持重复元素是否可以修改是否有序,等 分为5类,分别是: 列表(list)、元组(tuple)、字符串(str)、集…...
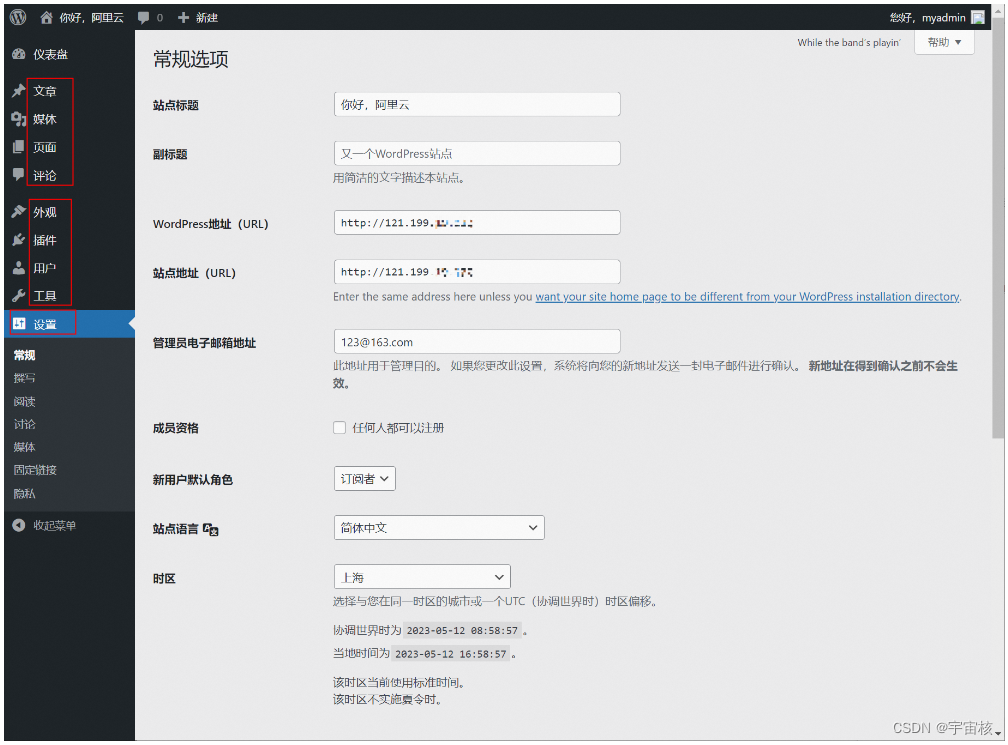
管理阿里云服务器ECS -- 网站选型和搭建
小云:我已经学会了如何登录云服务器ECS了,但是要如何搭建网站呢? 老王:目前有很多的个人网站系统软件,其中 WordPress 是使用非常广泛的一款,而且也可以把 WordPress 当作一个内容管理系统(CMS…...
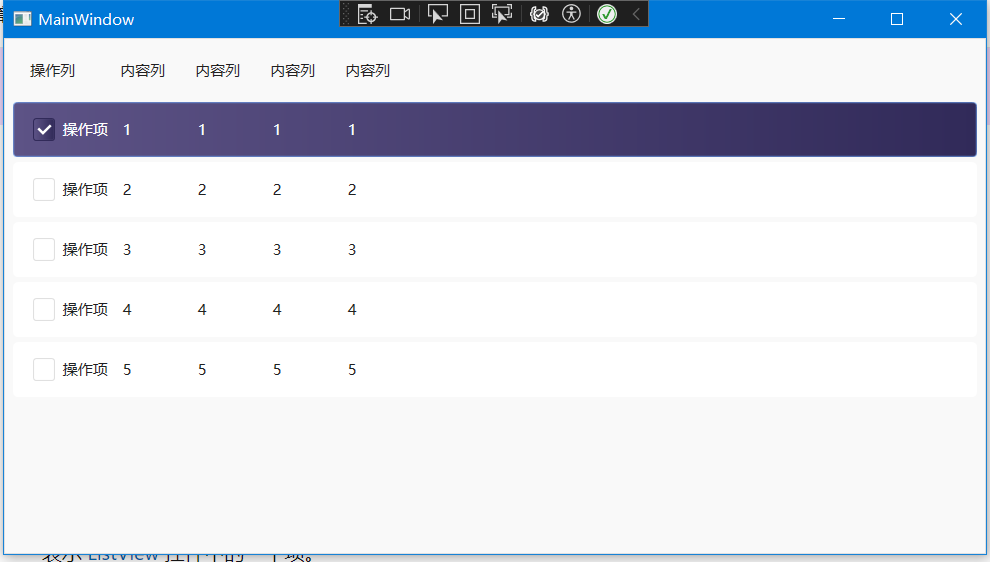
WPF中继承ItemsControl子类控件数据模板获取选中属性
需求场景 列表类控件,如 ListBox、ListView、DataGrid等。显示的行数据中,部分内容依靠选中时触发控制,例如选中行时行记录复选,部分列内容控制显隐。 案例源码以ListView 为例。 Xaml 部分 <ListView ItemsSource"{Bi…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
