【Java数据结构】关于栈的操作出栈,压栈,中缀表达式,后缀表达式,逆波兰表达式详解

🔥个人主页:努力学编程’
🔥内容管理:java数据结构

上一篇文章我们讲过了java数据结构的链表,对于链表我们使用了它的一些基本操作,完成了扑克牌小游戏的操作,如果你感兴趣的话,点击超链接观看:【java数据结构】基于java提供的ArrayList实现的扑克牌游戏-(附源码~),今天带大家学习的是数据结构中另一个非常重要的知识-栈
目录
- 1栈的一些基础知识
- java代码实现一个栈
- 对于栈功能的详解
- 1.压栈:
- 2.出栈pop:
- 3.获取栈顶元素peek:
- 逆波兰表达式求值:
- 中缀表达式:
- 后缀表达式:
- 那么如何实现中缀表达式和后缀表达式的转换:
- 解题思路:
- 代码实现
1栈的一些基础知识
在开始前,请牢记这句话:栈是一种先进后出的数据结构。栈(stack)是限定仅在表的一端进行操作的数据结构,请联系我们前文所学的,设想一个单链表我们只能够对其链表的表尾结点进行操作,而操作也只能够进行插入一个新的结点与删除最末尾的这个结点两个操作,而这样强限制性的‘链表’,就是我们所说的栈。
栈在底层逻辑的实现上可分为链表栈和数组栈:
栈分为数组栈和链表栈,其区别是数组栈使用数组进行功能的模拟,实现较为快速和便利,而链表栈使用链表的思路去设计,实现较为麻烦,但是其稳定不易出错;在链表栈中又分为静态链表栈和动态链表栈,静态链表栈给定栈的空间大小,不允许超过存储超过给定数据大小的元素,而动态栈使用的是自动创建空间的方法进行创建,只要符合机器的硬件要求以及编译器的控制,其理论上是极大的。
以下是实现一个栈的具体操作过程:
1.选择数据结构:
栈可以使用数组(或列表)或链表来实现。数组实现的栈通常更简单,因为它们具有随机访问的能力,而链表实现的栈可能需要更多的指针操作。
2.定义栈的操作:
定义栈的基本操作,包括入栈(push)、出栈(pop)、获取栈顶元素(peek)等。
3.确定栈的大小(如果有限制): 如果栈有大小限制,则需要确定栈的最大容量。如果栈的大小是动态的,则可以跳过此步骤。
4.实现栈的基本操作:
根据选择的数据结构,实现栈的基本操作。如果使用数组实现,通常使用数组的末尾作为栈的顶部,入栈操作将元素添加到数组末尾,出栈操作将从数组末尾移除元素。如果使用链表实现,需要定义节点类,并根据栈的操作更改节点的连接关系。
5.处理边界情况:
在实现栈的操作时,要考虑边界情况,如栈为空时尝试出栈或查看栈顶元素,或者栈已满时尝试入栈。
6.测试栈的实现:
编写测试代码,确保栈的实现能够正常工作,并处理各种情况,如入栈、出栈、查看栈顶元素、栈为空或栈已满等。
7.优化(如果需要):
根据实际需求和性能要求,可以对栈的实现进行优化,例如使用动态数组实现以处理栈大小动态变化的情况,或者使用链表实现以节省内存空间。
通过以上步骤,你可以实现一个简单而有效的栈数据结构。
java代码实现一个栈
import java.util.ArrayList;
import java.util.EmptyStackException;public class Stack {private ArrayList<Integer> stack;private int maxSize;// 构造函数public Stack(int maxSize) {this.maxSize = maxSize;this.stack = new ArrayList<>();}// 判断栈是否为空public boolean isEmpty() {return stack.isEmpty();}// 判断栈是否已满public boolean isFull() {return stack.size() == maxSize;}// 入栈操作public void push(int item) {if (isFull()) {System.out.println("Stack is full. Cannot push element.");} else {stack.add(item);}}// 出栈操作public int pop() {if (isEmpty()) {throw new EmptyStackException();}return stack.remove(stack.size() - 1);}// 获取栈顶元素但不移除public int peek() {if (isEmpty()) {throw new EmptyStackException();}return stack.get(stack.size() - 1);}// 获取栈的大小public int size() {return stack.size();}// 主函数用于测试public static void main(String[] args) {Stack stack = new Stack(5);// 入栈操作stack.push(1);stack.push(2);stack.push(3);stack.push(4);stack.push(5);// 获取栈的大小System.out.println("Stack size: " + stack.size());// 出栈操作System.out.println("Pop element: " + stack.pop());System.out.println("Pop element: " + stack.pop());// 获取栈顶元素System.out.println("Peek element: " + stack.peek());// 获取栈的大小System.out.println("Stack size: " + stack.size());}
}对于栈功能的详解
1.压栈:
向栈里插入数据,称为压栈,下面为图解:
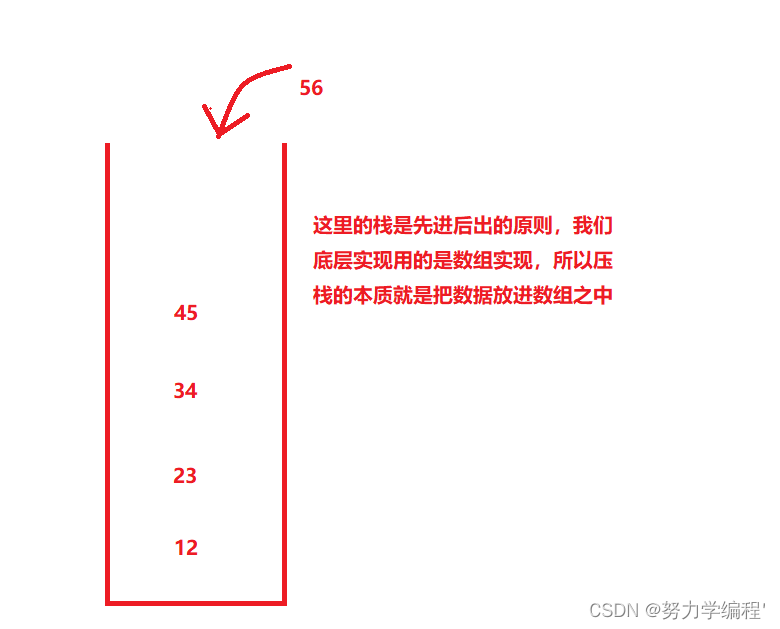
既然栈我们底层用的是数组实现,那么在我们压栈的时候,就必须考虑一件事情,数组是否已满,如果数组已经放满了,我们就必须先对数组进行扩容,然后才能对数据进行插入
那么具体应该如何对栈实现扩容呢,其实和数组扩容是一个道理:
public void push(int val){if(isFull()){Arrays.copyOf(elem,2*elem.length);}elem[usedSize]=val;usedSize++;}public boolean isFull(){return usedSize== elem.length;}
2.出栈pop:
将栈顶的元素弹出,后面的元素接替成为栈顶元素,属于栈的基本操作
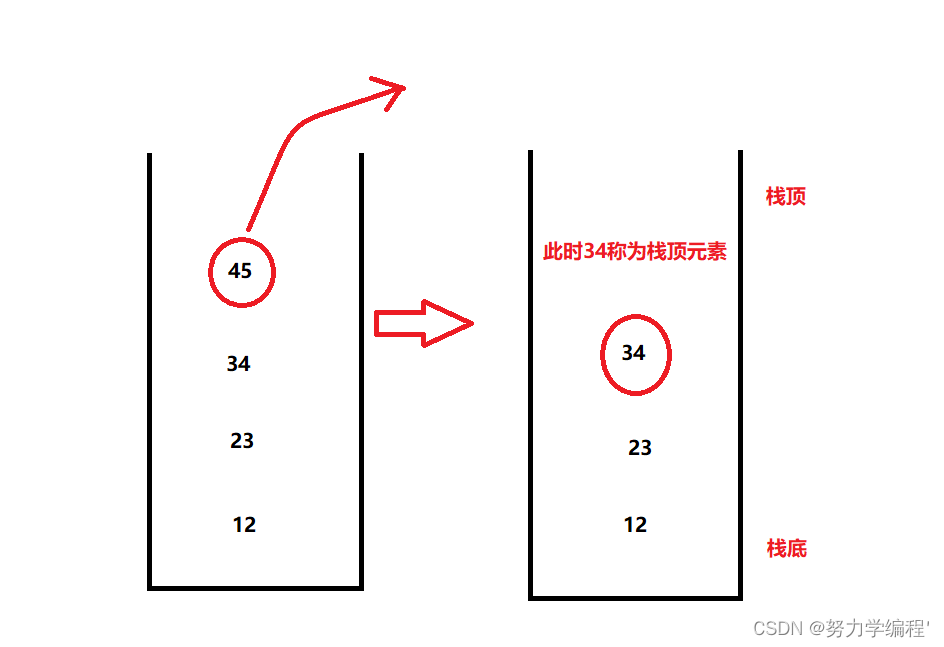
下面是使用java实现的pop方法:
public int pop(){if(empty()){return -1;}int oldVal=elem[usedSize-1];usedSize--;return oldVal;}public boolean empty(){return usedSize==0;}
将栈顶的元素返回,具体对于栈数据的删除,其实就是将usedSize–,代表将数组的大小进行了调整。
3.获取栈顶元素peek:
本质上其实就是将栈顶元素进行打印,需要注意的一点这个方法返回栈顶的元素但不移除它。
public int pop(){if(empty()){return -1;}int oldVal=elem[usedSize-1];usedSize--;return oldVal;}public boolean empty(){return usedSize==0;}public int peek(){if(empty()){return -1;}return elem[usedSize-1];}
}
以上就是对于栈的一些基本操作,了解完这些知识,我们就可以使用栈的知识解决一些算法题。
逆波兰表达式求值:
点击链接一起挑战,逆波兰表达式求值要想解决这道题,我们需要首先了解中缀表达式,后缀表达式的知识
中缀表达式:
中缀表达式是我们最常见的数学表达式形式,它采用操作符位于操作数之间的形式。例如,“3 + 4”、“(5 - 2) * 6” 等都是中缀表达式。
中缀表达式的特点包括:
1.操作符在操作数中间:例如,“3 + 4” 中的加号就位于操作数 3 和 4 之间。
2.使用括号:中缀表达式通常需要使用括号来明确运算的优先级和顺序。
3.常见的运算符优先级规则:乘除法优先于加减法,同级运算符按照从左到右的顺序计算。
后缀表达式:
后缀表达式,也称为逆波兰表达式(Reverse Polish Notation,RPN),是一种不需要括号来表示运算顺序的数学表达式形式。在后缀表达式中,操作符在操作数之后出现,因此不需要括号来明确运算的顺序。
后缀表达式的主要特点是:
1.没有括号:
不需要括号来指定运算次序,因为操作符始终跟在操作数之后。
2.明确运算顺序:
从左到右扫描表达式,每当遇到一个操作符,就从栈中弹出足够的操作数进行计算,然后将结果压回栈中,直到整个表达式扫描完毕。
3.简化计算:
后缀表达式减少了运算符的优先级问题,简化了计算过程。
例如,将中缀表达式 "3 + 4 * 5" 转换为后缀表达式为 "3 4 5 * +"。
处理后缀表达式的算法通常使用栈来实现。具体步骤如下:
1.从左到右遍历后缀表达式的每个字符。
2.如果遇到操作数,则将其压入栈中。
3.如果遇到操作符,则从栈中弹出相应数量的操作数进行运算,并将结果压入栈中。
4.最终栈中只剩下一个元素,即为后缀表达式的计算结果。
那么如何实现中缀表达式和后缀表达式的转换:
这里给大家分享一个方法:
1.首先将表达式严格改为中缀表达式
2.把每个运算符转移到对应括号的后面
3.完成后缀表达式的转化

解题思路:
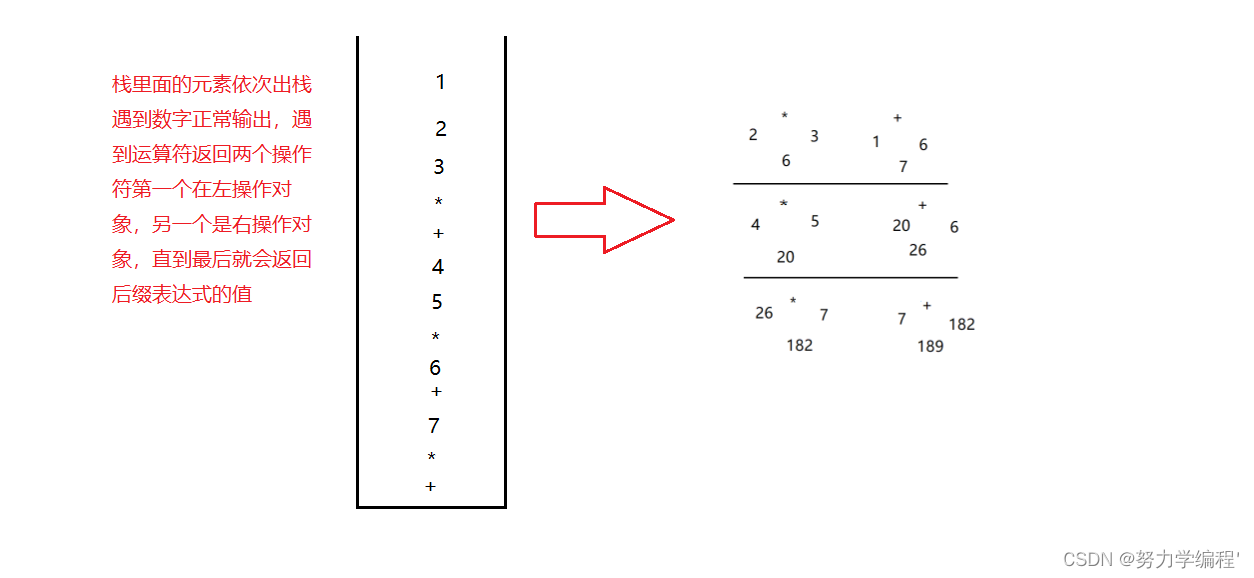
代码实现
public int evalRPN(String[] tokens) {int n = tokens.length;int[] stack = new int[(n + 1) / 2];int index = -1;for (int i = 0; i < n; i++) {String token = tokens[i];switch (token) {case "+":index--;stack[index] += stack[index + 1];break;case "-":index--;stack[index] -= stack[index + 1];break;case "*":index--;stack[index] *= stack[index + 1];break;case "/":index--;stack[index] /= stack[index + 1];break;default:index++;stack[index] = Integer.parseInt(token);}}return stack[index];}
好了,今天就分享到这里,谢谢大家!
相关文章:

【Java数据结构】关于栈的操作出栈,压栈,中缀表达式,后缀表达式,逆波兰表达式详解
🔥个人主页:努力学编程’ 🔥内容管理:java数据结构 上一篇文章我们讲过了java数据结构的链表,对于链表我们使用了它的一些基本操作,完成了扑克牌小游戏的操作,如果你感兴趣的话,点…...
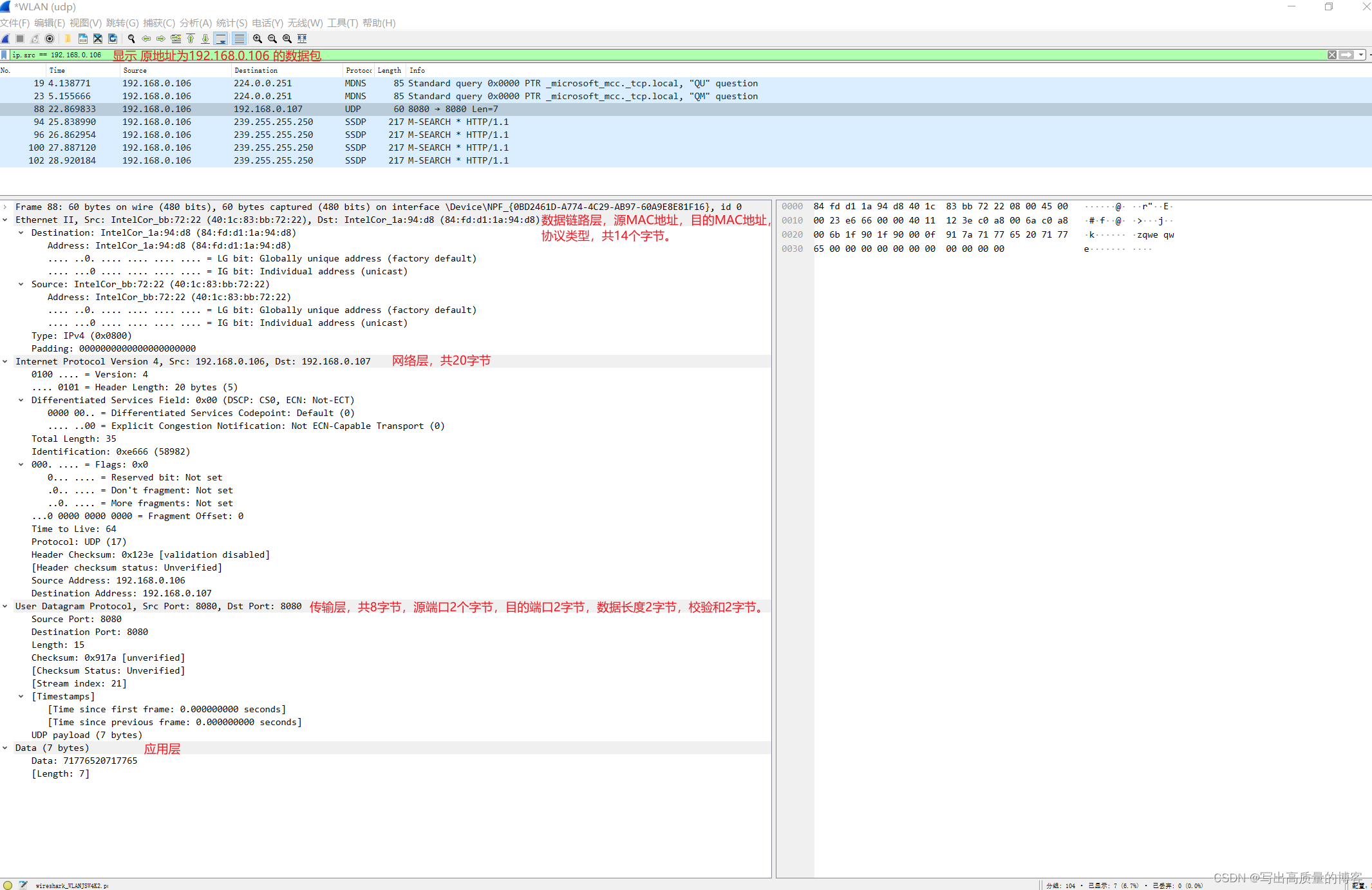
wireshark 使用
wireshark介绍 wireshak可以抓取经过主机网卡的所有数据包(包括虚拟机使用的虚拟网卡的数据包)。 环境安装 安装wireshark: https://blog.csdn.net/Eoning/article/details/132141665 安装网络助手工具:https://soft.3dmgame.com/down/213…...

C++纯虚函数的使用
纯虚函数是一种在C中定义抽象基类的方法,它是一个在基类中声明但没有实现的虚函数。 纯虚函数需要在派生类中进行实现,否则派生类也会成为抽象类,无法直接实例化对象。 下面是关于纯虚函数的讲解和代码示例: 纯虚函数的定义&#…...
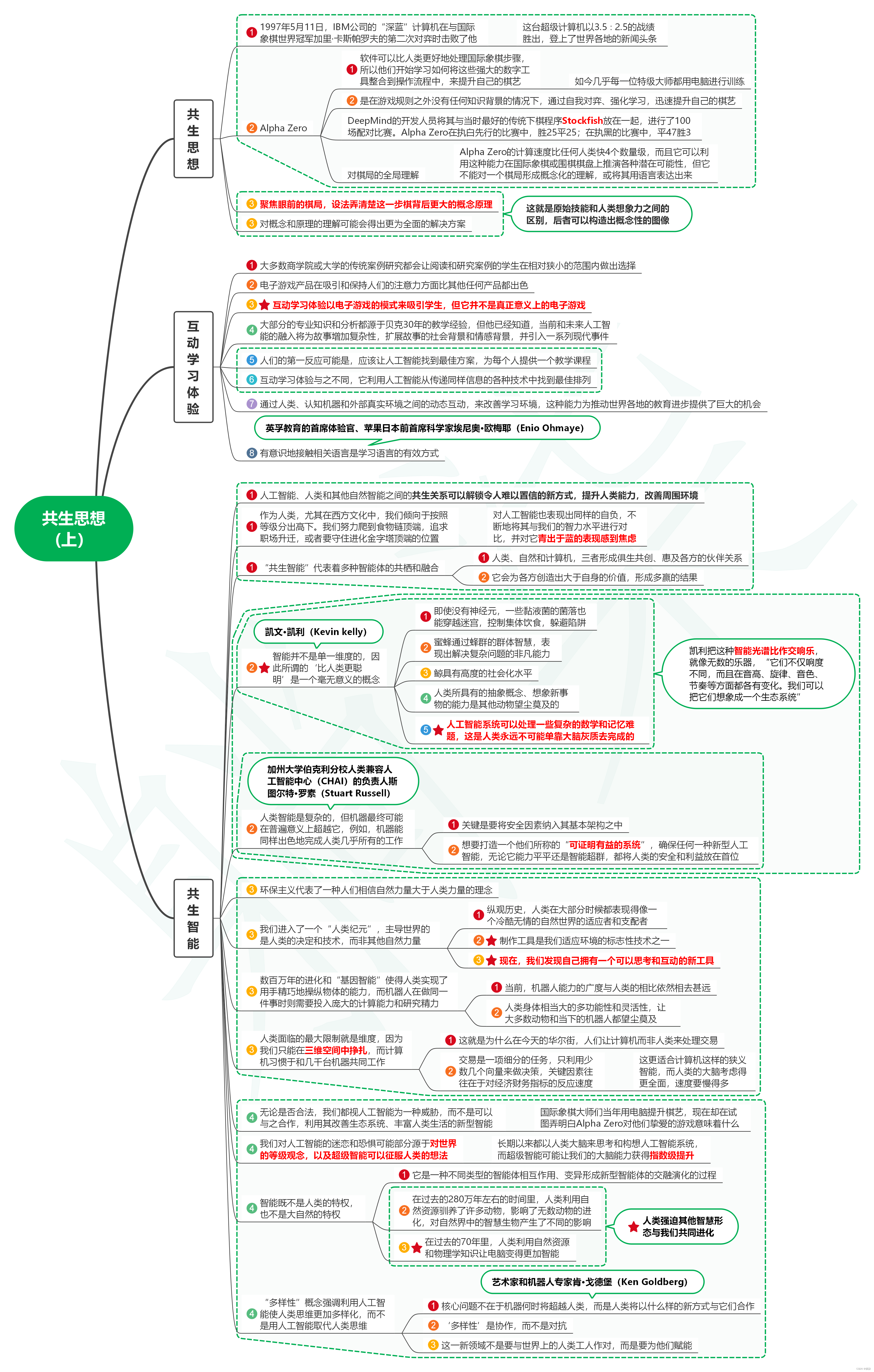
读所罗门的密码笔记06_共生思想(上)
1. 共生思想 1.1. 1997年5月11日,IBM公司的“深蓝”计算机在与国际象棋世界冠军加里卡斯帕罗夫的第二次对弈时击败了他 1.1.1. 这台超级计算机以3.5∶2.5的战绩胜出,登上了世界各地的新闻头条 1.2. Alpha Zero 1.2.…...
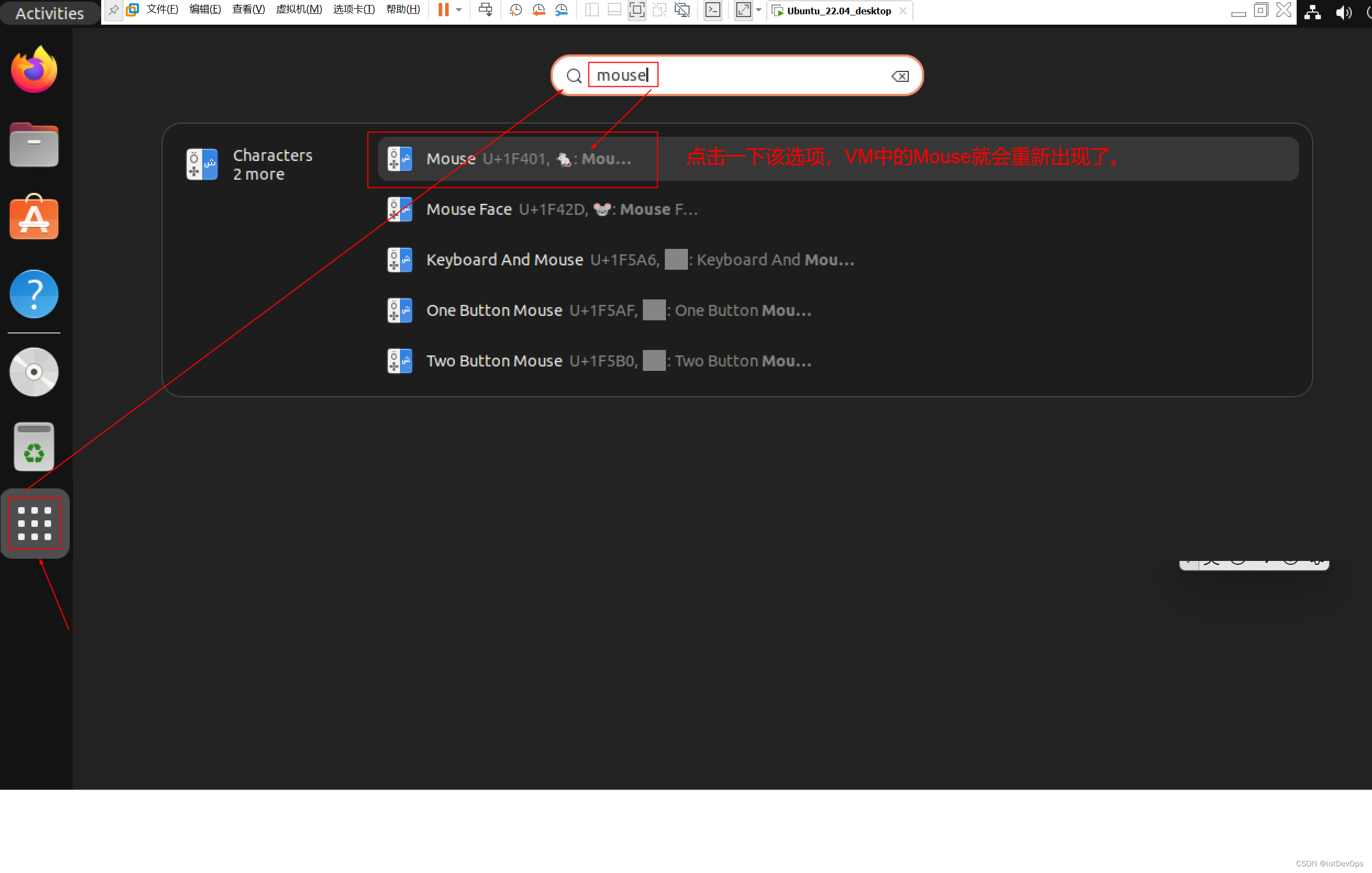
QA:ubuntu22.04.4桌面版虚拟机鼠标丢失的解决方法
前言 在Windows11中的VMWare Workstation17.5.1 Pro上安装了Ubuntu22.04.4,在使用过程中发现,VM虚拟机的鼠标的光标会突然消失,但鼠标其他正常,就是光标不见了,下面是解决办法。 内容 如下图,输入mouse&a…...

idea从零开发Android 安卓 (超详细)
首先把所有的要准备的说明一下 idea 2023.1 什么版本也都可以操作都是差不多的 gradle 8.7 什么版本也都可以操作都是差不多的 Android SDK 34KPI 下载地址: AndroidDevTools - Android开发工具 Android SDK下载 Android Studio下载 Gradle下载 SDK Tools下载 …...
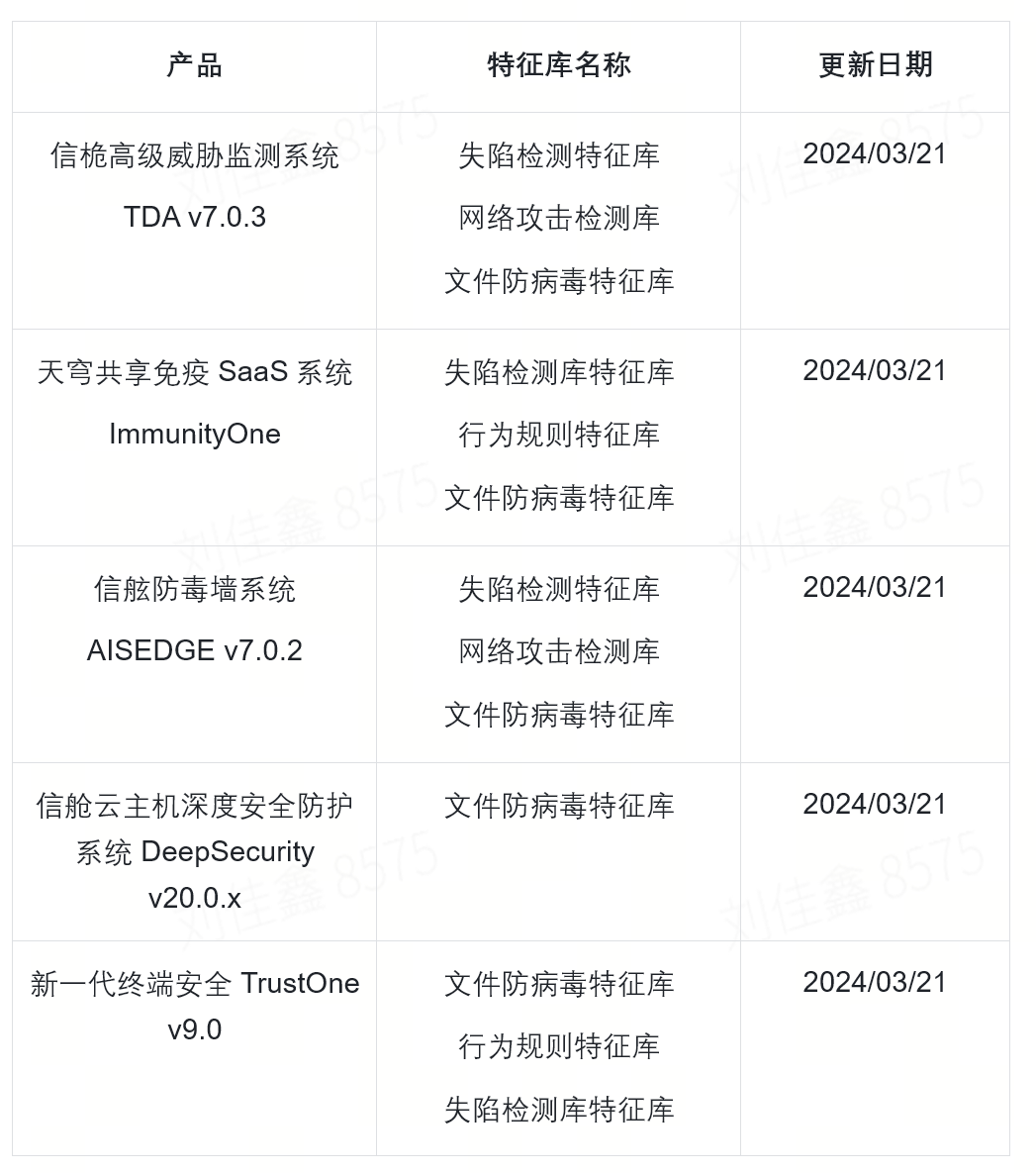
1.5T数据惨遭Lockbit3.0窃取,亚信安全发布《勒索家族和勒索事件监控报告》
本周态势快速感知 本周全球共监测到勒索事件93起,近三周攻击数量呈现持平状态。 本周Lockbit3.0是影响最严重的勒索家族,Blacksuit和Ransomhub恶意家族紧随其后,从整体上看Lockbit3.0依旧是影响最严重的勒索家族,需要注意防范。 …...
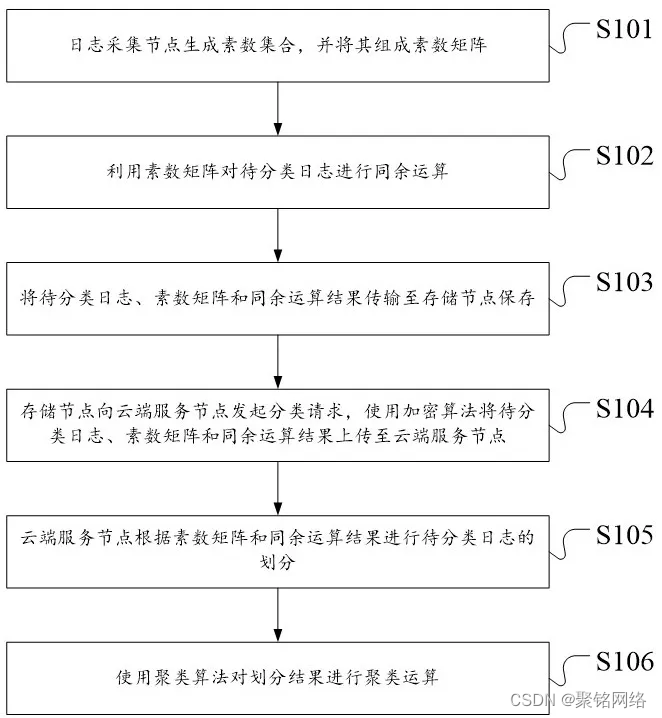
喜讯!聚铭网络荣获《日志分类方法及系统》发明专利
近日,聚铭网络又喜获一项殊荣,其申报的《日志分类方法及系统》发明专利成功获得国家知识产权局的授权,正式荣获国家发明专利证书。 在信息化时代,网络安全问题日益凸显,日志分析作为保障网络安全的重要手段ÿ…...

每日一博 - 关于日志记录的最佳实践
文章目录 概述选择合适的日志等级打印函数的入参、出参打印日志对象要做判空处理,避免阻断流程推荐使用 Slf4j不用e.printStackTrace()打印日志低级别的日志输出,必须进行日志级别开关判断不打印重复日志打印全部的异常信息,方便定位问题核心…...

针对pycharm打开新项目需要重新下载tensorflow的问题解决
目录 一、前提 二、原因 三、解决办法 一、前提 下载包之前,已经打开了,某个项目。 比如:我先打开了下面这个项目: 然后在terminal使用pip命令下载: 如果是这种情况,你下载的这个包一般都只能用在这一个…...

<商务世界>《第29课 外贸展会上应注意的事项》
1 参展前需要知道的问题 1)在开展前,是否发邀请给外商,告诉他们你的展位号,你的企业及产品的优势? 2)你的展位布置是否能够吸引外商? 3)你参展的产品是否具有个性,特色&…...

sklearn主成分分析PCA
文章目录 基本原理PCA类图像降维与恢复 基本原理 PCA,即主成分分析(Principal components analysis),顾名思义就是把矩阵分解成简单的组分进行研究,而拆解矩阵的主要工具是线性变换,具体形式则是奇异值分解。 设有 m m m个 n n …...
linux命令之tput
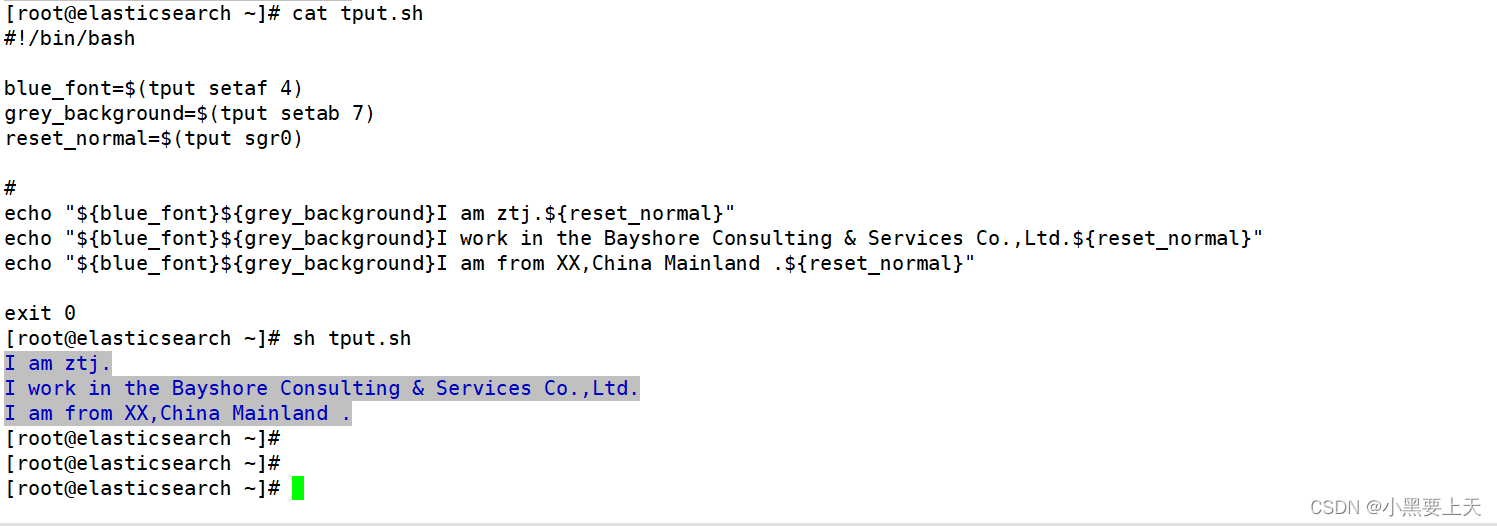
1.tput介绍 linux命令tput是可以在终端中进行文本和颜色的控制和格式化,其是一个非常有用的命令 2.tput用法 命令: man tput 3.样例 3.1.清除屏幕 命令: tput clear [rootelasticsearch ~]# tput clear [rootelasticsearch ~]# 3.2.…...
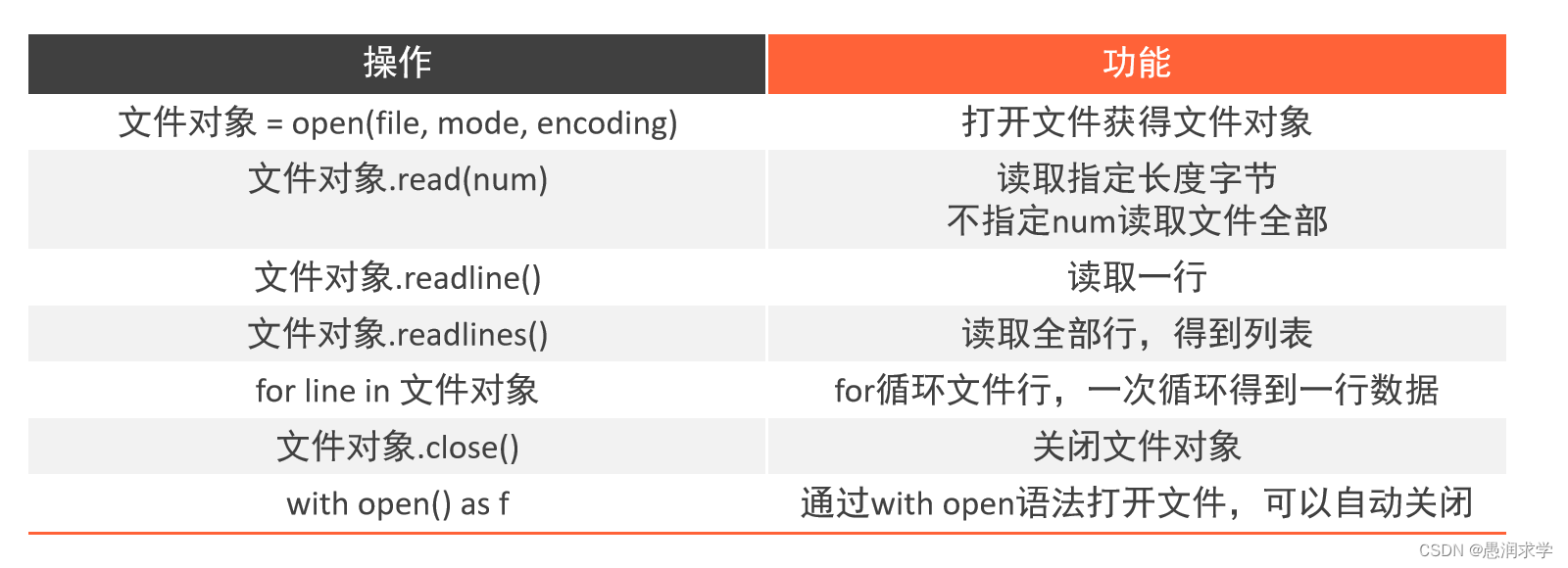
python基础——文件操作【文件编码、文件的打开与关闭操作、文件读写操作】
📝前言: 这篇文章主要讲解一下python中对于文件的基础操作: 1,文件编码 2,文件的打开与关闭操作 3,文件读写操作 🎬个人简介:努力学习ing 📋个人专栏:C语言入…...

rustup update 升级rust时异常 directory does not exist: ‘share/doc/rust/html‘ 解决方法
最近把原来的老版本rust升级为最新版本, 转悠了半天给我报一个 目录不存在异常而升级失败。 异常信息: info: rolling back changes error: failure removing component rust-docs-x86_64-apple-darwin, directory does not exist: share/doc/rust/ht…...
算法学习——LeetCode力扣动态规划篇5
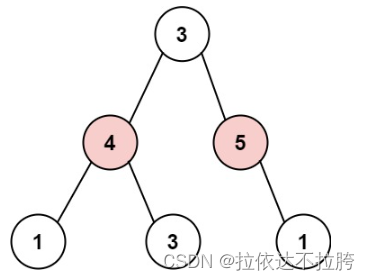
算法学习——LeetCode力扣动态规划篇5 198. 打家劫舍 198. 打家劫舍 - 力扣(LeetCode) 描述 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统…...

C语言-文件
目录 1.什么是文件?1.1 程序文件1.2 数据文件 2.二进制文件和文本文件?3.文件的打开和关闭4.文件的顺序读写5.文件的随机读写5.1 fseek5.2 ftell5.3 rewind 6.文件读取结束的判定7.文件缓冲区 1.什么是文件? 磁盘上的文件就是文件 一般包含两…...

牛客NC30 缺失的第一个正整数【simple map Java,Go,PHP】
题目 题目链接: https://www.nowcoder.com/practice/50ec6a5b0e4e45348544348278cdcee5 核心 Map参考答案Java import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可…...
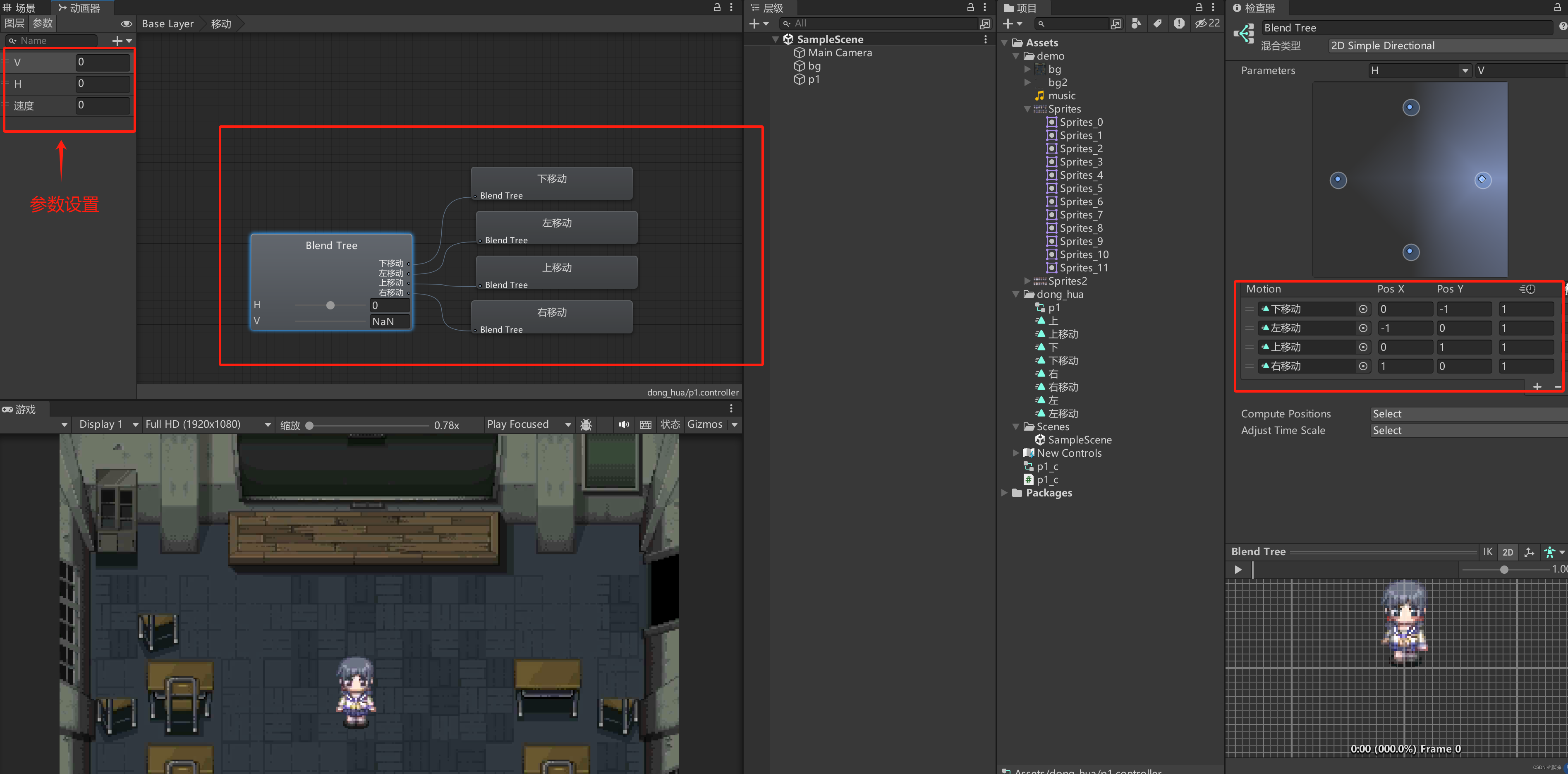
Unity 基于Rigidbody2D模块的角色移动
制作好站立和移动的动画后 控制器设计 站立 移动 角色移动代码如下: using System.Collections; using System.Collections.Generic; using Unity.VisualScripting; using UnityEngine;public class p1_c : MonoBehaviour {// 获取动画组件private Animator …...
Stata 15 for Mac:数据统计分析新标杆,让研究更高效!
Stata 是一种统计分析软件,适用于数据管理、数据分析和绘图。Stata 15 for Mac 具有以下功能: 数据管理:Stata 提供强大的数据管理功能,用户可以轻松导入、清洗、整理和管理数据集。 统计分析:Stata 提供了广泛的统计…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
