sklearn主成分分析PCA
文章目录
- 基本原理
- PCA类
- 图像降维与恢复
基本原理
PCA,即主成分分析(Principal components analysis),顾名思义就是把矩阵分解成简单的组分进行研究,而拆解矩阵的主要工具是线性变换,具体形式则是奇异值分解。
设有 m m m个 n n n维样本 X = ( x 1 , x 2 , ⋯ , x m ) X=(x_1, x_2,\cdots,x_m) X=(x1,x2,⋯,xm),但这 n n n个维度彼此并不完全独立,所以想试试有没有办法将其降低到 k k k维,则PCA的主要流程为
- 先将原始数据按列组成 n n n行 m m m列矩阵 X X X,然后对每一行数据进行中心化 x i j = x i j − 1 m ∑ j = 1 m x j x_{ij}=x_{ij}-\frac{1}{m}\sum^m_{j=1}x_j xij=xij−m1∑j=1mxj,记中心化之后的矩阵为 x ′ x' x′
- 计算样本协方差矩阵,由于已经中心化,故可表示为 C = 1 m X ′ X ′ T C=\frac{1}{m}X'X'^T C=m1X′X′T
- 计算协方差矩阵的特征值和特征向量,一般需要用到奇异值分解
- 对特征向量按照特征值大小进行排序,取前 k k k组特征向量组成矩阵 P P P,则 P X PX PX就是 k k k维的主成分
由于矩阵乘法的几何意义是坐标系的旋转、平移以及缩放,所以从几何角度理解PCA,就是将坐标系旋转到尽量与更多样本平行,从而达到简化坐标轴的作用。就好比一条空间中的直线,需要用三个维度来表示,但这条直线是一维的,只需旋转、移动坐标轴,使得这条直线与 x x x轴重合,就能只用一个坐标来表示这条直线。
PCA类
【PCA】类是sklearn.decomposition中用以实现主成分分析的类,其构造函数为
PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', n_oversamples=10, power_iteration_normalizer='auto', random_state=None)
各参数含义如下
n_components组分个数,默认为样本数和特征数中较小的那个;如果输入为小数,则表示百分之几copy为False时,将覆盖原始数据。whitenbool为True时, 对组分矢量进行如下操作:先乘以样本的方根,然后除以奇异值svd_solver奇异值求解器,可选'auto', 'full', 'arpack', 'randomized'tol容忍度random_state用于设置随机数种子power_iteration_normalizer设置SVD分解方案,可选"LU", "QR", "auto", "none四种。当svd_solver设为arpack时不可用。
奇异值求解器共有4个选择, 其中full将调用scipy.linalg.svd,计算稠密矩阵比较快;arpack将调用scipy.sparse.linalg.svds,更擅长计算稀疏矩阵。二者的具体区别可见scipy奇异值分解💎稀疏矩阵SVD
图像降维与恢复
下面用scipy中经典的楼梯图像来测试一下主成分分析。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import decompositionfrom scipy.misc import ascent
img = ascent()sh = img.shape
ns = [256, 128, 64, 32, 16, 5]imgs = [img]
for i in ns[1:]:pca = decomposition.PCA(i)# 彩色图像需要先转化为矩阵再进行PCAimNew = pca.fit_transform(img.reshape(sh[0], -1))im = pca.inverse_transform(imNew)imgs.append(im.reshape(sh))fig = plt.figure()
for i, im in enumerate(imgs):ax = fig.add_subplot(231+i)ax.imshow(im)plt.title(str(ns[i]))plt.axis('off')plt.show()
【fit_transform】对图像进行降维,保留相应组分并输出
【inverse_transofrm】对图像进行恢复,最终得到的效果如下,随着组分的逐渐降低,图像也越来越模糊。

相关文章:

sklearn主成分分析PCA
文章目录 基本原理PCA类图像降维与恢复 基本原理 PCA,即主成分分析(Principal components analysis),顾名思义就是把矩阵分解成简单的组分进行研究,而拆解矩阵的主要工具是线性变换,具体形式则是奇异值分解。 设有 m m m个 n n …...
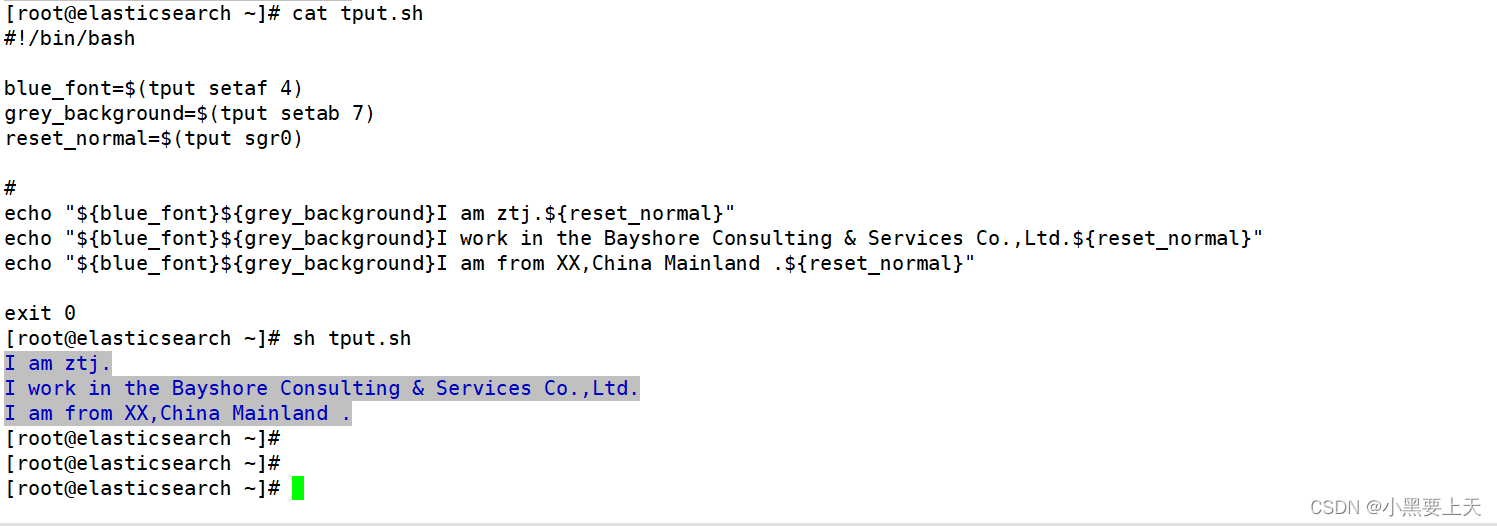
linux命令之tput
1.tput介绍 linux命令tput是可以在终端中进行文本和颜色的控制和格式化,其是一个非常有用的命令 2.tput用法 命令: man tput 3.样例 3.1.清除屏幕 命令: tput clear [rootelasticsearch ~]# tput clear [rootelasticsearch ~]# 3.2.…...
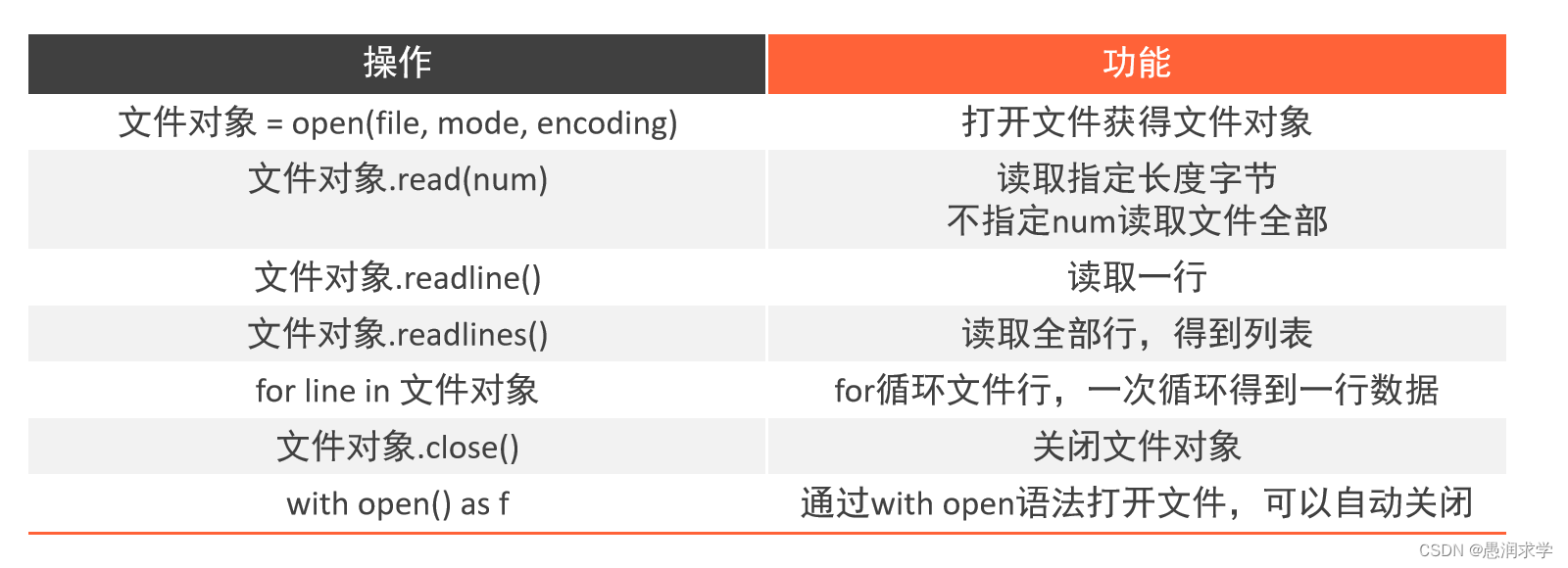
python基础——文件操作【文件编码、文件的打开与关闭操作、文件读写操作】
📝前言: 这篇文章主要讲解一下python中对于文件的基础操作: 1,文件编码 2,文件的打开与关闭操作 3,文件读写操作 🎬个人简介:努力学习ing 📋个人专栏:C语言入…...

rustup update 升级rust时异常 directory does not exist: ‘share/doc/rust/html‘ 解决方法
最近把原来的老版本rust升级为最新版本, 转悠了半天给我报一个 目录不存在异常而升级失败。 异常信息: info: rolling back changes error: failure removing component rust-docs-x86_64-apple-darwin, directory does not exist: share/doc/rust/ht…...
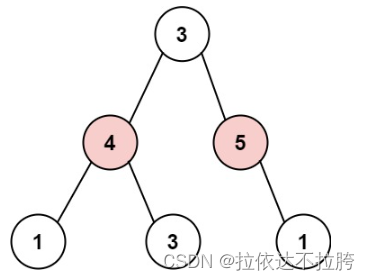
算法学习——LeetCode力扣动态规划篇5
算法学习——LeetCode力扣动态规划篇5 198. 打家劫舍 198. 打家劫舍 - 力扣(LeetCode) 描述 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统…...

C语言-文件
目录 1.什么是文件?1.1 程序文件1.2 数据文件 2.二进制文件和文本文件?3.文件的打开和关闭4.文件的顺序读写5.文件的随机读写5.1 fseek5.2 ftell5.3 rewind 6.文件读取结束的判定7.文件缓冲区 1.什么是文件? 磁盘上的文件就是文件 一般包含两…...

牛客NC30 缺失的第一个正整数【simple map Java,Go,PHP】
题目 题目链接: https://www.nowcoder.com/practice/50ec6a5b0e4e45348544348278cdcee5 核心 Map参考答案Java import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可…...
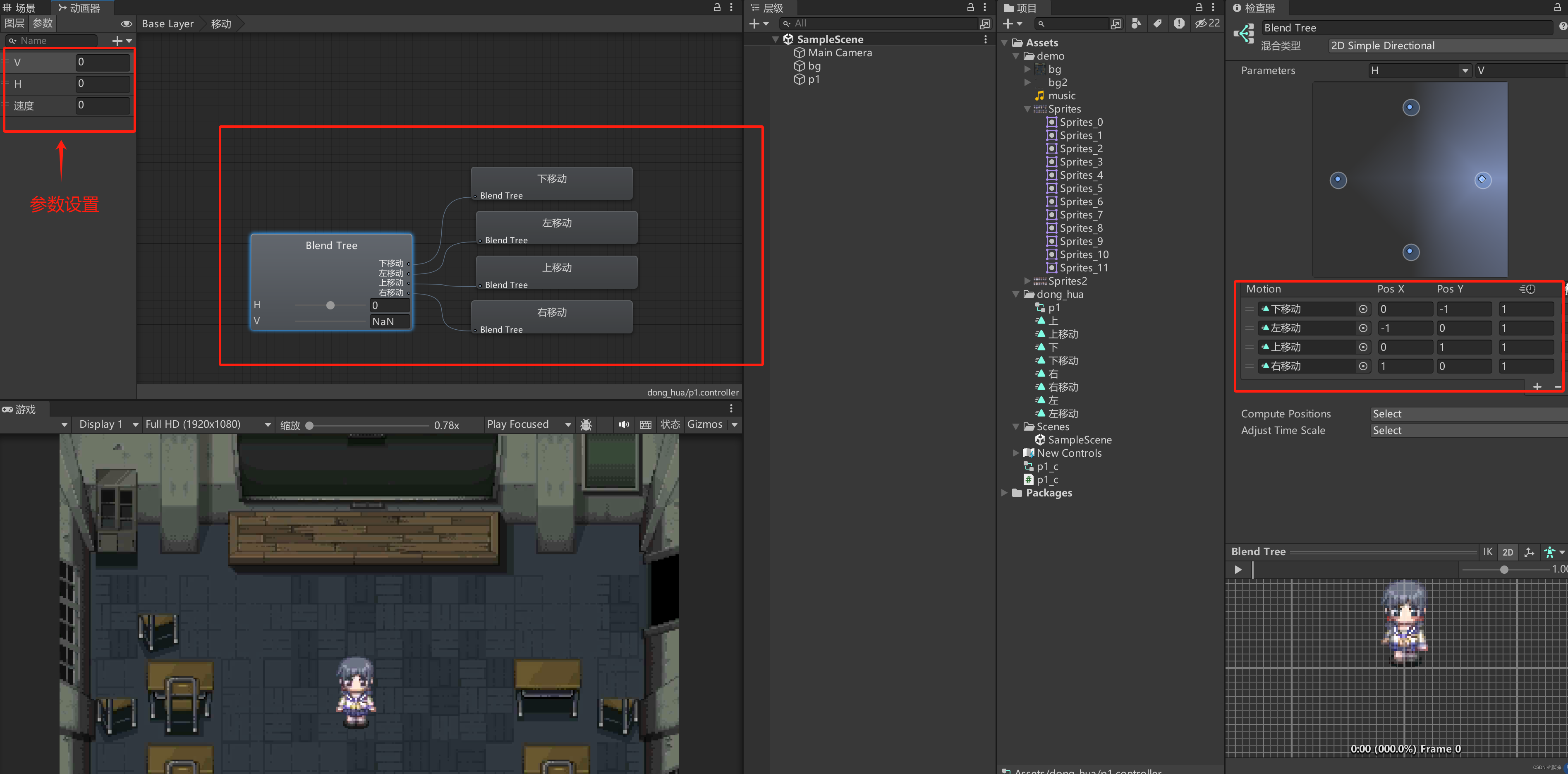
Unity 基于Rigidbody2D模块的角色移动
制作好站立和移动的动画后 控制器设计 站立 移动 角色移动代码如下: using System.Collections; using System.Collections.Generic; using Unity.VisualScripting; using UnityEngine;public class p1_c : MonoBehaviour {// 获取动画组件private Animator …...
Stata 15 for Mac:数据统计分析新标杆,让研究更高效!
Stata 是一种统计分析软件,适用于数据管理、数据分析和绘图。Stata 15 for Mac 具有以下功能: 数据管理:Stata 提供强大的数据管理功能,用户可以轻松导入、清洗、整理和管理数据集。 统计分析:Stata 提供了广泛的统计…...

vue配置代理proxy
如何配置代理 在 vue devServer服务器配置文件 vue.config.js 的 devServer 选项中配置 proxy module.exports {// publicPath:process.env.NODE_ENV production ? /vue_workspac/aihuhuproject/ : /,//基本路径publicPath: ./,//默认的/是绝对路径,如果不确定在…...

.NET DES加密算法实现
简介: DES(Data Encryption Standard)加密算法作为一种历史悠久的对称加密算法,自1972年由美国国家标准局(NBS)发布以来,广泛应用于各种数据安全场景。本文将从算法原理、优缺点及替代方案等方…...

构建操作可靠的数据流系统
文章目录 前言数据流动遇到的困难先从简单开始可靠性延迟丢失 性能性能损失性能——分层重试 可扩展性总结 前言 在流式架构中,任何对非功能性需求的漏洞都可能导致严重后果。如果数据工程师没有将可伸缩性、可靠性和可操作性等非功能性需求作为首要考虑因素来构建…...

awesome-cheatsheets:超级速查表 - 编程语言、框架和开发工具的速查表
awesome-cheatsheets:超级速查表 - 编程语言、框架和开发工具的速查表,单个文件包含一切你需要知道的东西 官网:GitHub - skywind3000/awesome-cheatsheets: 超级速查表 - 编程语言、框架和开发工具的速查表,单个文件包含一切你需…...

GFW不起作用
闲着折腾,刷openwrt到一个小米3G路由器后,GFW不起作用。后面发现是自己电脑设置了DNS,解析完IP后,在经过代代,IP不在GFW的清单里,所以转发控制就没有起作用。 结论 在经过代代前的所有节点,都…...
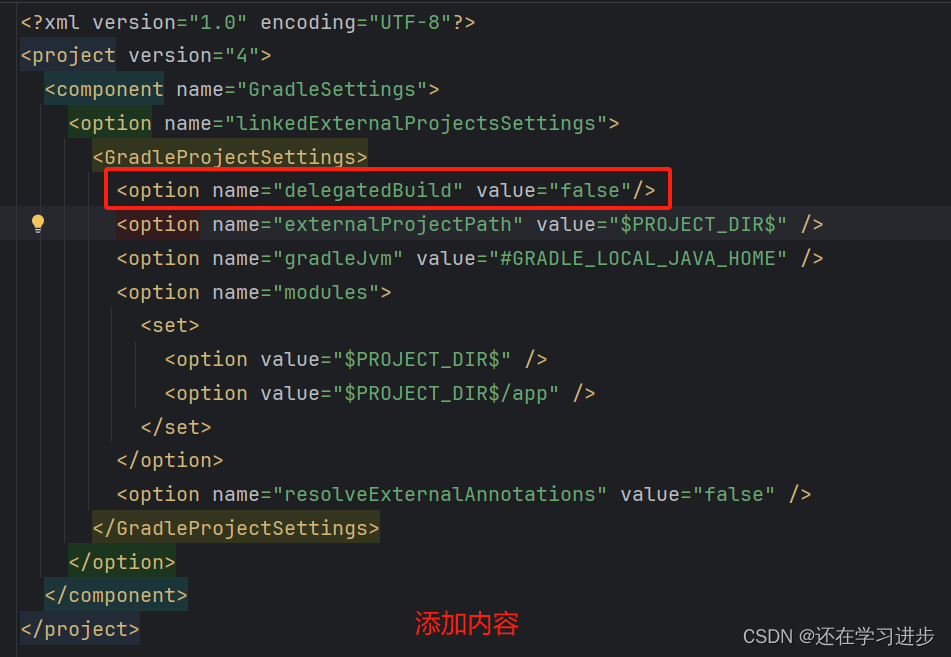
AndroidStudio出现类似 Could not create task ‘:app:ToolOperatorDemo.main()‘. 错误
先看我们的报错 翻译过来大概意思是:无法创建任务:app:ToolOperatorDemo.main()。 没有找到名称为“main”的源集。 解决方法: 在.idea文件夹下的gradle.xml文件中 <GradleProjectSettings>标签下添加<option name"delegatedBuild" value"f…...

一些常见的ClickHouse问题和答案
什么是ClickHouse?它与其他数据库系统有什么区别? ClickHouse是一个开源的列式数据库管理系统(DBMS),专门用于高性能、大规模数据分析。与传统的行式数据库相比,ClickHouse具有更高的查询性能、更高的数据…...
第九届蓝桥杯大赛个人赛省赛(软件类)真题C 语言 A 组-分数
solution1 直观上的分数处理 #include <iostream> using namespace std; int main() {printf("1048575/524288");return 0; }#include<stdio.h> #include<math.h> typedef long long ll; struct fraction{ll up, down; }; ll gcd(ll a, ll b){if…...

并发编程——4.线程池
这篇文章我们来讲一下线程池的相关内容 目录 1.什么是线程池 1.1为什么要用线程池 1.2线程池的优势 2.线程池的使用 3.线程池的关闭 4.线程池中的execute和submit方法的一些区别 5.线程池的参数和原理 6.自定义线程池 7.总结 1.什么是线程池 1.1为什么要用线程池 首…...
阿里云魔搭发起“ModelScope-Sora开源计划”,将为中国类Sora模型开发提供一站式工具链
在2024年3月23日的全球开发者先锋大会上,阿里云的魔搭社区宣布了一个新计划:“ModelScope-Sora开源计划”。这个计划旨在通过开源方式,帮助中国在Sora模型类型上做出更多创新。这个计划提供了一整套工具,包括处理数据的工具、多模…...

大模型与数据分析:探索Text-to-SQL
当今大模型如此火热,作为一名数据同学,持续在关注LLM是如何应用在数据分析中的,也关注到很多公司推出了AI数智助手的产品,比如火山引擎数智平台VeDI—AI助手、 Kyligence Copilot AI数智助理、ThoughtSpot等,通过接入人…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
