保研线性代数机器学习基础复习1

1.什么是代数（algebra）?

为了形式化一个概念，构建出有关这个概念的符号以及操作符号的公式。

2.什么是线性代数（linear algebra）？

一项关于向量以及操作向量的公式的研究。

3.举一些向量的例子？

• 几何向量（Gemometric vectors）：可以进行add操作也可以multiply by标量，帮助我们在方向direction和大小magnitude方面去推理数学操作。
• 多项式（Polynomial）：y=x2+x3+x4...
• 音频信号（Audio signals）：音频信号是一系列数字，我们可以把音频信号加和（add），亦可以以一定λ大小扩大（multiply）。
• ：n元组是指n维向量，也是为了方便编程语言中array的表示。

4.什么是线性方程组（system of linear equation）？

其中，是这个式子的未知量，每一个满足这个方程组的n元组都可以称为线性方程组的一个解。

5.实数线性方程组的解（solution）有哪些情况？

要么无解，要么有一个解，要么有多个解。

如果是，那么可以看做二维平面两条直线相交，那么结果是1.无交集2.一个点3.一条直线。如果是，那么可以看做是在三维立体空间两个平面相交，结果可能是1.一个平面2.一条直线3.一个点4.空。

6.什么是点积（dot product），也称作Hadamard product?

对于元素，我们用矩阵A的第i行与矩阵B的第j列逐个元素相乘，然后相加。

7.什么是单位矩阵（Identity Matrix）？

在n阶方阵中，只是在对角（diagonal）元素值为1，在其他元素值为0。

8.矩阵有哪些性质（property）？

• 结合性：
• 分配性：
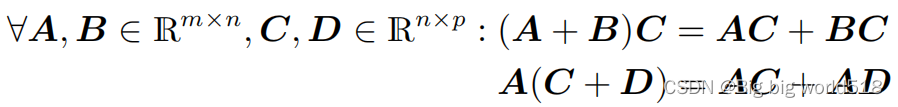
• 和单位矩阵相乘：

9.什么是矩阵的逆（inverse）？

对于n行n列的矩阵A和n行n列的矩阵B，如果满足，B被叫做A的逆。如果B存在，那么称A为正则矩阵/可逆矩阵/非奇异矩阵（regular/invertible/nonsingular）。如果矩阵的行列式（determinant）不为零，那么可以认为矩阵可逆。

10.什么是矩阵的转置（transpose）？

对于m行n列的矩阵A，A的转置B是n行m列，A的每一行作为B的每一列。如果A可逆，那么B（A的转置）爷可逆。

11.关于矩阵的逆和矩阵的转置的性质？

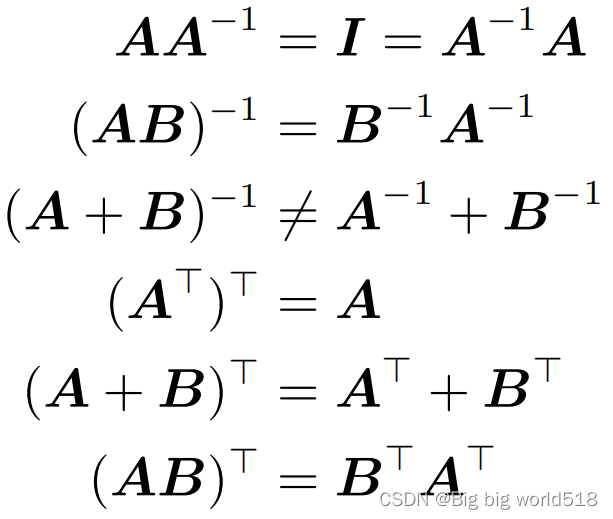
12.求解线性方程组的过程？

• 寻找的特解
• 寻找的所有解
• 将步骤一和步骤二的所有解结合起来得到通解（general solution）

13.什么是高斯消元法（Gaussian elimination）

高斯消元法是通过初等变换（elementary transformation）把一个线性方程组的增广矩阵（augmented matrix），譬如，那么其增广矩阵为，变成一个行递减的形式（reduced row-echelon）。

14.行递减阶梯矩阵有什么特点？

• 是一个行阶梯的形式
• 每个枢轴的值都是1
• 每一列只有唯一一个枢轴是这一列不为零的值

15.什么是广义逆矩阵（Moore-Penrose pseudo-inverse）？

通常情况我们定义逆矩阵针对的是方阵，但是如果一个非方阵矩阵，它的各个列向量是线性无关（linear independent），那么我们我们可以使用如下方法求解：

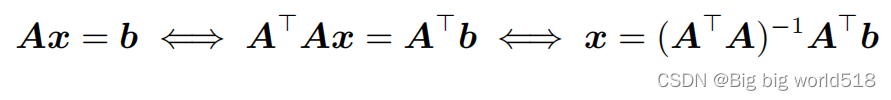
其中解被称为广义逆矩阵。