素数的计数律:Π函数、歪斜数
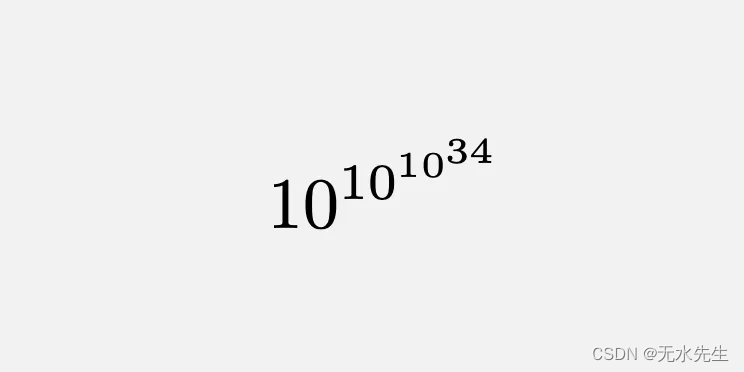
相当多的数字!
一、说明
自从人类开始掌握最起码的算术概念以来,有一类数字一直处于最前沿——素数。素数定义简单,但难以捕捉,众所周知,素数是数学中一些最困难问题的罪魁祸首,让几代最优秀的数学家感到困惑。
“直到今天,数学家们都徒劳地试图在素数序列中发现某种秩序,我们有理由相信这是一个人类思维永远无法穿透的奥秘。” ~ 莱昂哈德·欧拉
二、素数(Prime)计数功能
也许这些问题中最著名的是这样的——给定一个数字 n,找到一个输出小于或等于 n 的素数的函数。所需的函数表示为 π(n)。
例如–
π(10) = 4 (2, 3, 5, 7)
π(17) = 7 (2, 3, 5, 7, 11, 13, 17)π(n), 1 ≤ n ≤ 60.来源。
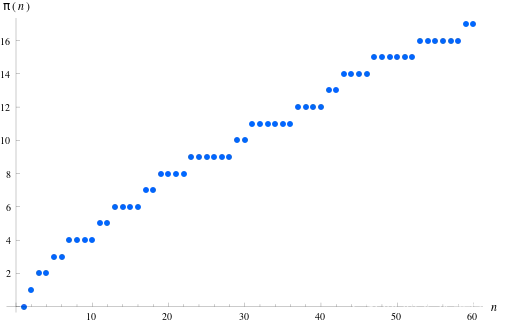
长期以来,寻找 π(n) 的闭合形式(精确)表达式一直是数学中最令人垂涎的问题之一。虽然没有人能够想出一个精确的表达式,但我们已经发现了一些强大的近似值!
三、素数计数函数的近似值
首先,谈谈我们在这里所说的近似值的含义。当我们说函数 f 近似于函数 g 时,这意味着对于足够大的 n 值,f(n) 和 g(n) 几乎相同,即出于实际目的,它们值之间的百分比差异可以安全地忽略(感兴趣的读者可以进一步查找 Big O 表示法)。即 f(n) ~ g(n) 对于大 n。
现在,我们介绍素数函数的两个最著名的近似值。
3.1 第一个近似
1) N/lnN:这里,ln 是自然对数,即以 e 为底的对数。这是素数函数的最简单近似值。令人惊讶的是,这种直截了当的表达式产生的值与 π(n) 非常吻合。此外,表达式通常输出小于 π(n) 的值,从而用作 π(n) 的非正式下限。
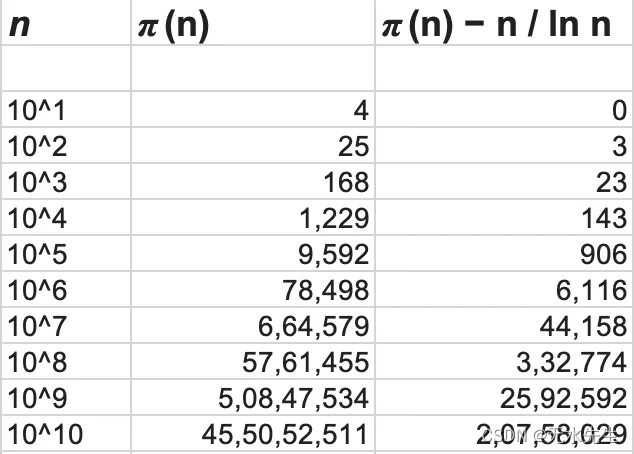
3.2 第二个近似函数
Li(N):第二个近似值是对数积分。此函数定义为
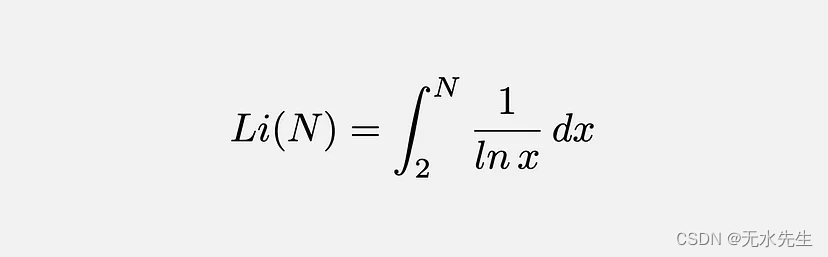
从图形上看,它是曲线 1/ln(x) 和 x 轴之间的面积,x 的范围从 2 到 N。
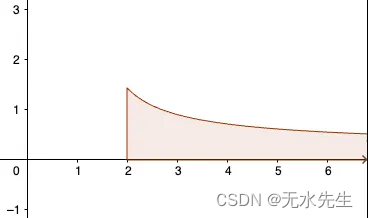
Li(N) 等于曲线 1/ln(x) 和 x 轴之间的面积,x 的范围从 2 到 N。
与前面的表达式不同,Li(N) 通常输出大于 π(n) 的值,从而作为 π(n) 的非正式上限。
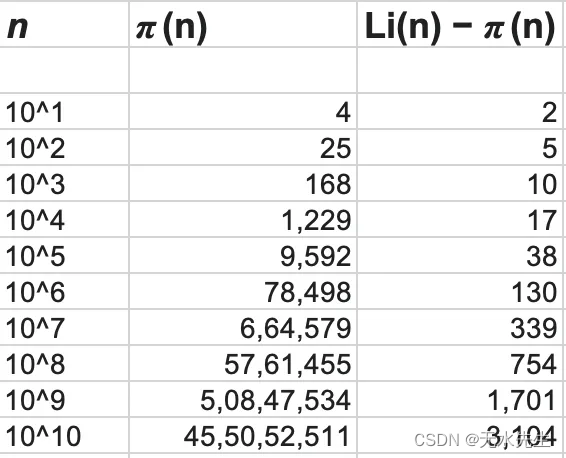
现在是有趣的部分。注意到上述陈述中使用了“正常”和“非正式”这两个词吗?他们是故意雇用的。请允许我详细阐述这两个词的重要性——
- “通常”:这意味着这些陈述对于我们出于实际目的所关注的典型价值范围是正确的,没有矛盾。
- “非正式”:但是没有数学证明这些陈述在任何地方都成立,即一直到无穷大。
那么,仅限于讨论 Li(N),对于一些较大的 N 值,它是否可能低于 π(N)?如果是,N 的值是多少?这正是本文的主要议程!
四、利特尔伍德的结果
在发现 Li(n) 作为 π(n) 的近似值后的许多年里,以下问题一直没有得到解答,困扰着当时最优秀的头脑——
Li(n) 是否> π(n) 适用于每个可能的 n?还是不平等在某个地方翻转?
人们已经尽可能高地计算了Li(n)值,但仍然没有一个反例被偶然发现。也许,许多人会认为不等式对 n 的所有值都成立。
最后,这个问题由当时英国领先的数学家之一 J.E. Littlewood 解决了——并且得到了肯定的解决!利特尔伍德证明了不等式确实翻转了某个足够大的 N 的符号,即存在一个 N,使得 Li(N) < π(N)。事实上,利特尔伍德证明了更多。他证明了不等式无限多次翻转符号!也就是说,如果我们看得足够高,我们会发现无限多的斑块,其中 Li(N) 占主导地位 π(N),反之亦然。确实有相当大的结果!

J.E.利特尔伍德(1885-1977)。来源。
但是,无论利特尔伍德的结果多么辉煌,它都缺少一件事——第一次翻转何时发生。其结果是数学中存在论证明的经典例子——断言某物存在,而没有指定任何特定的例子,甚至没有指定构建一个算法。
因此,即使在利特尔伍德取得重大进展之后,问题仍然存在——不平等何时会出现翻转迹象?我们至少可以有一些上限吗?
确切地说,这就是留给 Littlewood 的学生 Skewes 来演示的!
五、歪斜数

斯坦利·斯凯斯(1899-1988)。来源。
斯坦利·斯凯斯(Stanley Skewes,1899-1988 年)是一位南非数学家,曾在剑桥大学师从利特尔伍德。在最初获得土木工程学位后,他移居英国学习数学,并于 1938 年获得博士学位。
Skewes 数是 Littlewood 发现的翻转的上限。也就是说,我们可以确定,对于某个小于 Skewes 数的数字,π(n) 会大于 Li(n)!
从理论上讲,不只有一个唯一的 Skewes 数。相反,其中有两个,取决于黎曼假设的有效性。对于外行来说,黎曼假设是整个数学中最令人垂涎的开放性问题,更不用说数论了。虽然深入探讨问题的细节超出了本文的范围,但以下理解就足够了——
-
第一歪斜数:假设黎曼假设为真,Skewes 在 1933 年表明,必须有一个小于 10(10(10³⁴)) 的数字,其中 π(n) 大于 Li(n)。通常,这个数字简称为 Skewes 数。难怪人们怀疑翻转是否真的发生了!即使对于今天强大的计算机来说,如此庞大的规模的计算也是无法实现的,更不用说一个世纪前的设备了。
-
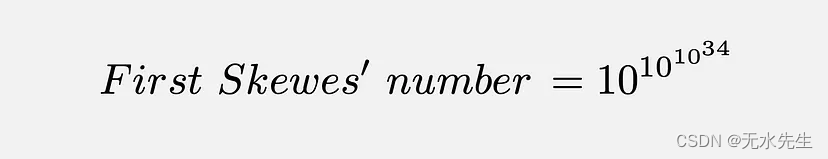
-
第二个 Skewes 数:如果黎曼假设是错误的,Skewes 还需要 22 年才能提出相应的极限。他 1955 年的结果证明,即使黎曼假设是错误的,π(n) 和 Li(n) 之间的翻转也必须发生在 10(10(10⁹⁶⁴)) 以下的某个地方。这是第二个 Skewes 的数字,显然比第一个更大!
-
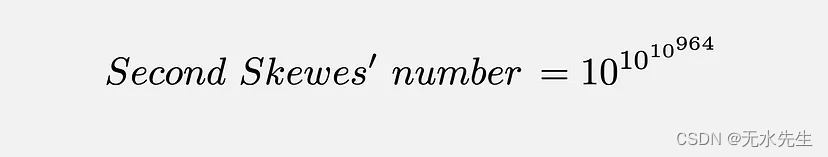
六、结论
伟大的英国数学家(也是利特尔伍德的长期合作者)G.H.哈代(G.H. Hardy)将Skewes的数字描述为——“[Skewes数]是数学中有史以来任何明确目的的最大数。” ~ G.H. 哈代
最重要的是,这句话突出了纯粹的数学家可以在多大程度上满足他们的求知欲。从实际的角度来看,Skewes的结果并没有做出任何实质性的贡献。即使我们忘记了它,世界也会保持不变。无论如何,谁愿意用一个甚至无法完全写下的数字做任何事情!?
但是,纯数学几乎不关心它的适用性。与艺术作品类似,像 Skewes 这样的数学结果有自己的粉丝追随者,无论多么小众。这就是纯数学的美妙和目的——它的存在是为了满足一群人的知识好奇心——跨越空间和时间!
相关文章:
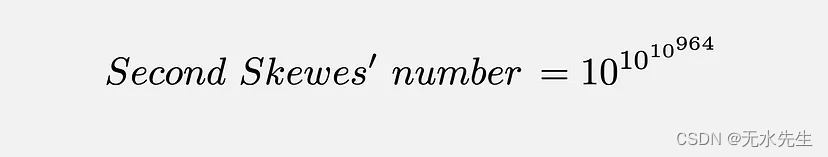
素数的计数律:Π函数、歪斜数
相当多的数字! 一、说明 自从人类开始掌握最起码的算术概念以来,有一类数字一直处于最前沿——素数。素数定义简单,但难以捕捉,众所周知,素数是数学中一些最困难问题的罪魁祸首,让几代最优秀的数学家感到…...

图像识别在农业领域的应用
图像识别技术在农业领域的应用正在逐渐成熟,它通过分析处理拍摄的植物或农田的图像,为农业生产提供决策支持。以下是图像识别在农业中的一些关键应用: 病虫害检测:图像识别技术能够识别作物上的病斑、虫害或异常状况。通过比较高…...
【JavaSE】java刷题--数组练习
前言 本篇讲解了一些数组相关题目(主要以代码的形式呈现),主要目的在于巩固数组相关知识。 上一篇 数组 讲解了一维数组和二维数组的基础知识~ 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎…...

预处理、编译、汇编、链接过程
预处理、编译、汇编、链接过程 预处理 引入头文件 #include 展开宏定义 #define 处理条件编译指令 #ifdef 删除注释 添加行号 在Linux下可以使用gcc -E命令把hello.c文件预处理成hello.i文件。windows这些操作都集成在编译器visual studio这些里面了。 编译 进行语法分…...

3、Cocos Creator 节点和组件
目录 1、 节点和组件 2、 节点层级和显示顺序 3、坐标系和节点变换属性 坐标系 锚点 旋转 缩放 尺寸 4、 常用技巧 5、参考 1、 节点和组件 Cocos Creator 的工作流程是以组件式开发为核心的,组件式架构也称作 组件 — 实体系统(或 Entity-C…...
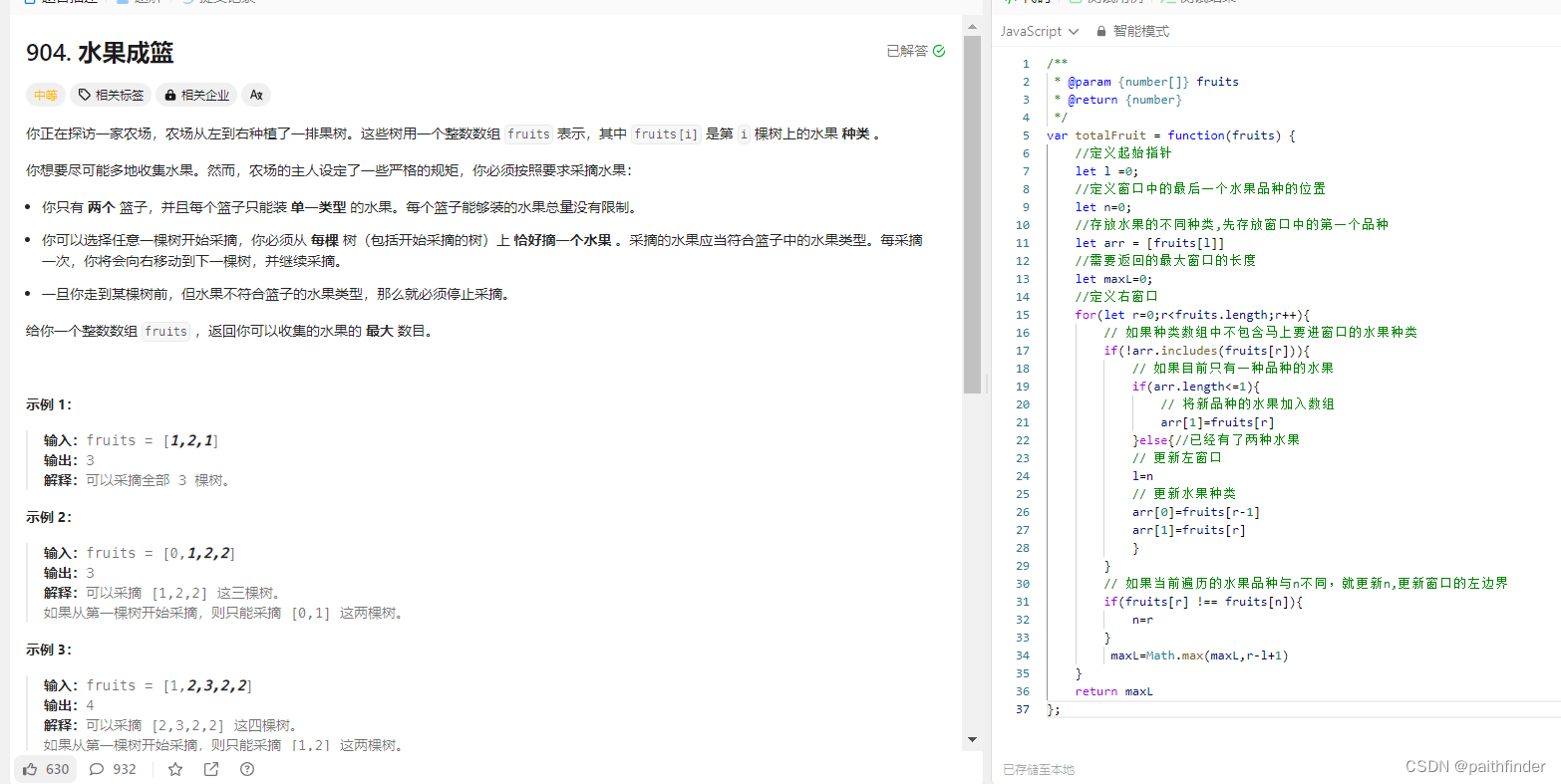
【js刷题:数据结构数组篇之长度最小的子数组】
长度最小的子数组 一、题目二、方法1.暴力解法2.滑动窗口是什么滑动窗口的起始位置滑动窗口的结束位置代码展示 3.力扣刷题水果成篮题目思路代码 一、题目 给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组&…...

大话设计模式之装饰模式
装饰模式(Decorator Pattern)是一种结构型设计模式,它允许向现有对象动态地添加新功能,同时又不改变其结构。装饰模式通过将对象放入包装器中来实现,在包装器中可以动态地添加功能。 在装饰模式中,通常会有…...

国赛大纲解读
1. 第一部分,是针对5G基础知识的掌握,第二部分是人工智能基本算法的掌握,就是人工智能的应用,用5G+人工智能(AI算法)进行网络优化的问题,要有网络优化的基础知识,比如说:某个区域的覆盖问题,覆盖特别差,但有数据,覆盖电频,srp值这些数据给你,根据数据来判断是…...
:原型模式)
设计模式(5):原型模式
一.原型模式 通过 n e w 产生一个对象需要非常繁琐的数据准备或访问权限,则可以使用原型模式。 \color{red}{通过new产生一个对象需要非常繁琐的数据准备或访问权限,则可以使用原型模式。} 通过new产生一个对象需要非常繁琐的数据准备或访问权限…...
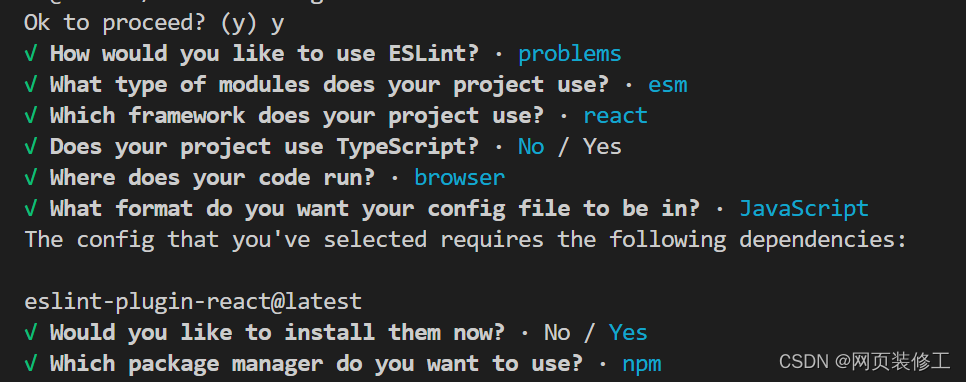
【React】vite + react 项目,进行配置 eslint
安装与配置 eslint 1 安装 eslint babel/eslint-parser2 初始化配置 eslint3 安装 vite-plugin-eslint4 配置 vite.config.js 文件5 修改 eslint 默认配置 1 安装 eslint babel/eslint-parser npm i -D eslint babel/eslint-parser2 初始化配置 eslint npx eslint --init相关…...
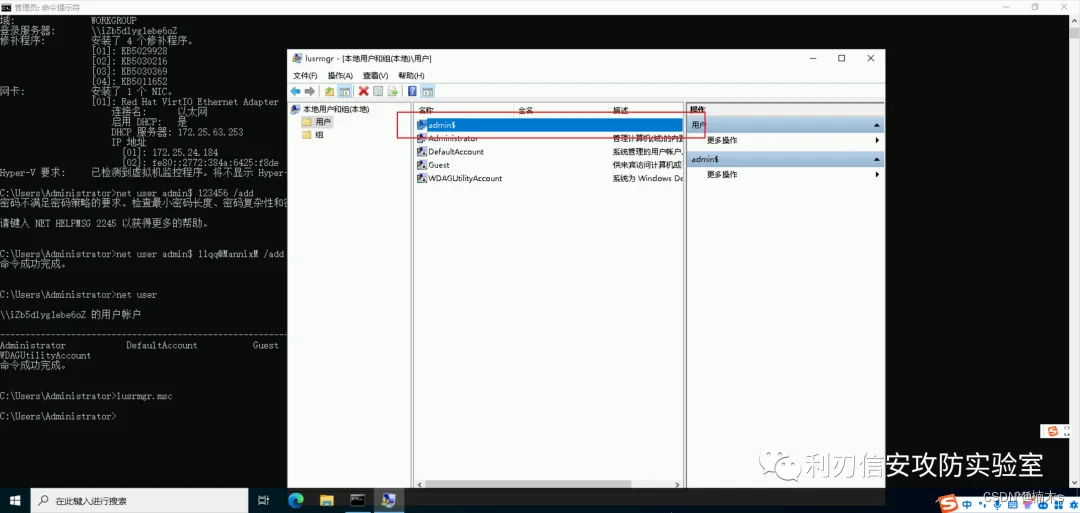
Windows入侵排查
目录 0x00 前言 0x01 入侵排查思路 1.1 检查系统账号安全 1.2 检查异常端口、进程 1.3 检查启动项、计划任务、服务 0x00 前言 当企业发生黑客入侵、系统崩溃或其它影响业务正常运行的安全事件时,急需第一时间进行处理,使企业的网络信息系统在最短时…...

C语言每日一题
1.题目 二.分析 本题有两点需要注意的: do-while循环 :在判断while条件前先执行一次do循环static变量 :程序再次调用时static变量的值不会重新初始化,而是在上一次退出时的基础上继续执行。for( i 1; i < 3; i )将调用两次…...

TheMoon 恶意软件短时间感染 6,000 台华硕路由器以获取代理服务
文章目录 针对华硕路由器Faceless代理服务预防措施 一种名为"TheMoon"的新变种恶意软件僵尸网络已经被发现正在侵入全球88个国家数千台过时的小型办公室与家庭办公室(SOHO)路由器以及物联网设备。 "TheMoon"与“Faceless”代理服务有关联,该服务…...

人脸68关键点与K210疲劳检测
目录 人脸68关键点检测 检测闭眼睁眼 双眼关键点检测 计算眼睛的闭合程度: 原理: 设置阈值进行判断 实时监测和更新 拓展:通过判断上下眼皮重合程度去判断是否闭眼 检测嘴巴是否闭合 提取嘴唇上下轮廓的关键点 计算嘴唇上下轮廓关键点之间的距…...

【跟着GPT4学JAVA】异常篇
JAVA异常中的知识点 问: 介绍下JAVA中的异常有哪些知识点吧 答: Java中的异常处理是一个重要的知识点,主要包括以下内容: 异常体系:Java的异常类是Throwable类派生出来的,Throwable下有两个重要的子类:Err…...
Ubuntu上安装d4rl数据集
Ubuntu上安装d4rl数据集 D4RL的官方 github: https://github.com/Farama-Foundation/D4RL 一、安装Mujoco 1.1 官网下载mujoco210文件 如果装过可以跳过这步 链接:https://github.com/deepmind/mujoco/releases/tag/2.1.0 下载第一个文件即可。我这里是在windo…...
之set 用法(创建、赋值、增删查改)详解)
C++之STL整理(4)之set 用法(创建、赋值、增删查改)详解
C之STL整理(4)之set 用法(创建、赋值、增删查改)详解 注:整理一些突然学到的C知识,随时mark一下 例如:忘记的关键字用法,新关键字,新数据结构 C 的map用法整理 C之STL整理…...
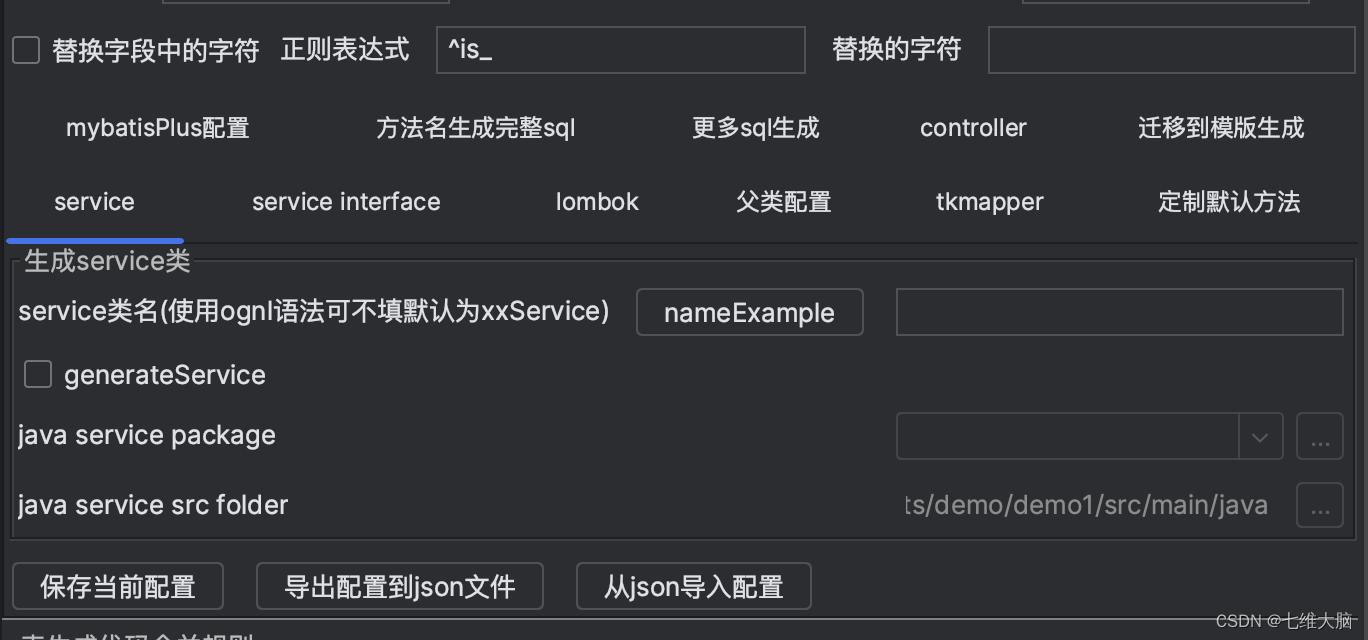
IDEA MyBatisCodeHelper Pro最新版(持续更新)
目录 0. 你想要的0.1 包下载0.2 使用jh 1. 功能介绍2. 下载安装2.1 在idea中插件市场安装2.2 在jetbrains插件市场下载安装 3. 简单使用3.1 创建一个SpringBoot项目3.2 配置数据库3.3 一键生成实体类、mapper 0. 你想要的 0.1 包下载 测试系统:Windows(…...
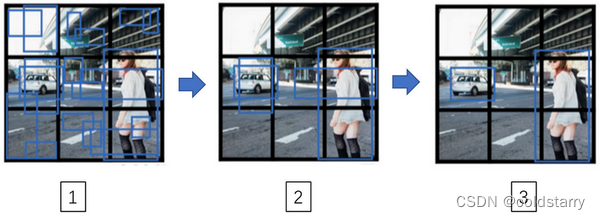
sheng的学习笔记-AI-YOLO算法,目标检测
AI目录:sheng的学习笔记-AI目录-CSDN博客 目录 目标定位(Object localization) 定义 原理图 具体做法: 输出向量 图片中没有检测对象的样例 损失函数 编辑 特征点检测(Landmark detection) 定义&a…...
C# wpf 嵌入wpf控件
WPF Hwnd窗口互操作系列 第一章 嵌入Hwnd窗口 第二章 嵌入WinForm控件 第三章 嵌入WPF控件(本章) 第四章 底部嵌入HwndHost 文章目录 WPF Hwnd窗口互操作系列前言一、如何实现?1、继承HwndHost2、添加Content属性3、创建wpf窗口并设置Conten…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

6.9本日总结
一、英语 复习默写list11list18,订正07年第3篇阅读 二、数学 学习线代第一讲,写15讲课后题 三、408 学习计组第二章,写计组习题 四、总结 明天结束线代第一章和计组第二章 五、明日计划 英语:复习l默写sit12list17&#…...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...
