算法学习——LeetCode力扣图论篇3(127. 单词接龙、463. 岛屿的周长、684. 冗余连接、685. 冗余连接 II)
算法学习——LeetCode力扣图论篇3

127. 单词接龙
127. 单词接龙 - 力扣(LeetCode)
描述
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk:
每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
示例
示例 1:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出:5
解释:一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。
示例 2:
输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出:0
解释:endWord “cog” 不在字典中,所以无法进行转换。
提示
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同
代码解析
深度搜索(超时)
class Solution {
public:int result = INT_MAX;int tmp_result = 1;int cheak(string s1 , string s2){int no_same_num = 0;for(int i=0 ; i<s1.size() ;i++){if(s1[i] != s2[i]) no_same_num++;}return no_same_num;}void track_back(string beginWord, string endWord, vector<string>& wordList , int indix, vector<bool> &path){for(int i=0 ; i<wordList.size() ;i++){if(wordList[indix] == endWord && path[i] == false){if(tmp_result < result) result = tmp_result;// cout<<endl;return;}else if(cheak(wordList[indix],wordList[i]) == 1 && path[i] == false){// cout<<wordList[i]<<' ';tmp_result ++;path[i] = true;track_back(beginWord,endWord,wordList,i,path);path[i] = false;tmp_result--;}}}int ladderLength(string beginWord, string endWord, vector<string>& wordList) {vector<bool> path(wordList.size(),false);for(int i=0 ; i<wordList.size() ;i++){if(cheak(beginWord,wordList[i]) == 1 && path[i]==false){// cout<<wordList[i]<<' ';path[i] = true;tmp_result++;track_back(beginWord,endWord,wordList,i,path);tmp_result--;path[i] = false;}}if(result == INT_MAX) return 0;return result;}
};
广度搜索
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {// 将vector转成unordered_set,提高查询速度unordered_set<string> wordSet(wordList.begin(), wordList.end());// 如果endWord没有在wordSet出现,直接返回0if (wordSet.find(endWord) == wordSet.end()) return 0;// 记录word是否访问过unordered_map<string, int> visitMap; // <word, 查询到这个word路径长度>// 初始化队列queue<string> que;que.push(beginWord);// 初始化visitMapvisitMap.insert(pair<string, int>(beginWord, 1));while(!que.empty()) {string word = que.front();que.pop();int path = visitMap[word]; // 这个word的路径长度for (int i = 0; i < word.size(); i++){string newWord = word; // 用一个新单词替换word,因为每次置换一个字母for (int j = 0 ; j < 26; j++) {newWord[i] = j + 'a';if (newWord == endWord) return path + 1; // 找到了end,返回path+1// wordSet出现了newWord,并且newWord没有被访问过if (wordSet.find(newWord) != wordSet.end() && visitMap.find(newWord) == visitMap.end()) {// 添加访问信息visitMap.insert(pair<string, int>(newWord, path + 1));que.push(newWord);}}}}return 0;}
};
463. 岛屿的周长
463. 岛屿的周长 - 力扣(LeetCode)
描述
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例
示例 1:
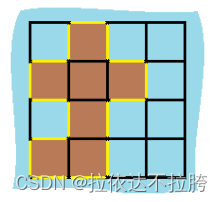
输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出:16
解释:它的周长是上面图片中的 16 个黄色的边
示例 2:
输入:grid = [[1]]
输出:4
示例 3:
输入:grid = [[1,0]]
输出:4
提示
row == grid.length
col == grid[i].length
1 <= row, col <= 100
grid[i][j] 为 0 或 1
代码解析
class Solution {
public:int result = 0;int m,n;int dir[4][2] = {0,-1,0,1,-1,0,1,0};void dfs(vector<vector<int>>& grid ,int x , int y){for(int i=0 ; i<4 ;i++){int next_x = x + dir[i][0];int next_y = y + dir[i][1];if(next_x<0||next_x>=m||next_y<0||next_y>=n) result++;else if(grid[next_x][next_y] == 0) result++;}return;}int islandPerimeter(vector<vector<int>>& grid) {m = grid.size();n = grid[0].size();for(int i=0 ; i<m ;i++){for(int j=0 ; j<n ;j++){if(grid[i][j] == 1)dfs(grid,i,j);}}return result;}
};
684. 冗余连接
684. 冗余连接 - 力扣(LeetCode)
描述
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的那个。
示例
示例 1:
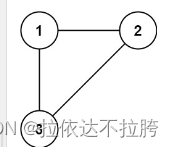
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]
示例 2:
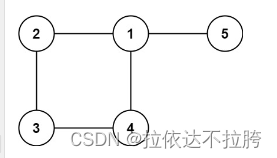
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
提示
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的
代码解析
class Solution {
public:int n = 0;int find(int u , vector<int> &father){if(u == father[u]) return father[u];father[u] = find(father[u] , father);return father[u];}void join(int u , int v , vector<int> &father){u = find(u , father);v = find(v , father);if(u == v) return;father[v] = u;}bool same(int u , int v , vector<int> &father){u = find(u , father);v = find(v , father);return u == v;}vector<int> findRedundantConnection(vector<vector<int>>& edges) {n = edges.size() + 1;vector<int> father(n,0);for(int i=0 ; i<n ; i++)father[i] = i;for(int i=0 ; i<edges.size() ; i++){if(same(edges[i][0] , edges[i][1] , father)) return edges[i];else join(edges[i][0] , edges[i][1] , father);}return {};}
};
685. 冗余连接 II
685. 冗余连接 II - 力扣(LeetCode)
描述
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例
示例 1:
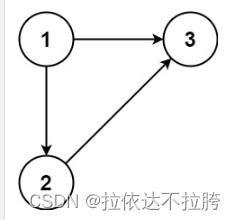
输入:edges = [[1,2],[1,3],[2,3]]
输出:[2,3]
示例 2:
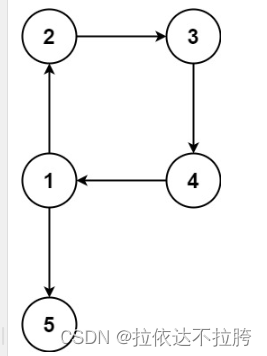
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出:[4,1]
提示
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ui, vi <= n
代码解析
class Solution {
public:int n=0;int find(int u , vector<int> &father){if(u == father[u]) return father[u];father[u] = find(father[u],father);return father[u];}void join(int u , int v , vector<int> &father ){u = find(u,father);v = find(v,father);if(u == v) return;father[v] = u; }bool same(int u , int v , vector<int> &father){u = find(u,father);v = find(v,father);return u == v;}bool tree_remove_edga(vector<vector<int>>& edges , int delete_edge , vector<int> &father){for(int i=0 ; i<n ;i++){if(i == delete_edge) continue;if(same(edges[i][0] , edges[i][1] , father) == true) return false;join(edges[i][0] , edges[i][1] , father);}return true;}vector<int> get_remove_edge(vector<vector<int>>& edges , vector<int> &father){for(int i=0 ; i<n ;i++){if(same(edges[i][0] , edges[i][1] , father) == true) return edges[i];join(edges[i][0] , edges[i][1] , father);}return {};}vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {n = edges.size();vector<int> father(n+1,0);vector<int> inDegree(n+1,0);for(int i=0 ; i<n ;i++){father[i] = i;inDegree[edges[i][1]] += 1;}father[n] = n;vector<int> inDeg_2;for(int i=n-1 ; i>=0 ;i--)if(inDegree[edges[i][1]] >= 2) inDeg_2.push_back(i);if(inDeg_2.size() > 0){if(tree_remove_edga(edges,inDeg_2[0] , father) == true) return edges[inDeg_2[0]];else return edges[inDeg_2[1]];}return get_remove_edge(edges,father);}
};
相关文章:

算法学习——LeetCode力扣图论篇3(127. 单词接龙、463. 岛屿的周长、684. 冗余连接、685. 冗余连接 II)
算法学习——LeetCode力扣图论篇3 127. 单词接龙 127. 单词接龙 - 力扣(LeetCode) 描述 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk: 每一对相…...

状态模式详解:管理对象状态的利器
在软件设计中,我们经常会遇到需要根据对象的不同状态来执行不同行为的情况。为了优雅地管理这些状态及其对应的行为,状态模式(State Pattern)应运而生。本文将深入探讨状态模式的使用条件、Java代码实现,并结合现实社会…...

探索----------------阿里云
目录 一、阿里云四大件 1、云服务器ECS 2、云数据库RDS 3、负载均衡SLB 4、对象存储OSS 5、其他的云计算产品 1)内容分发网络CDN 2)专有网络 VPC 二、linux发行版本 三、你平时对系统会怎么优化(五大负载) 1、cpu 使用率…...
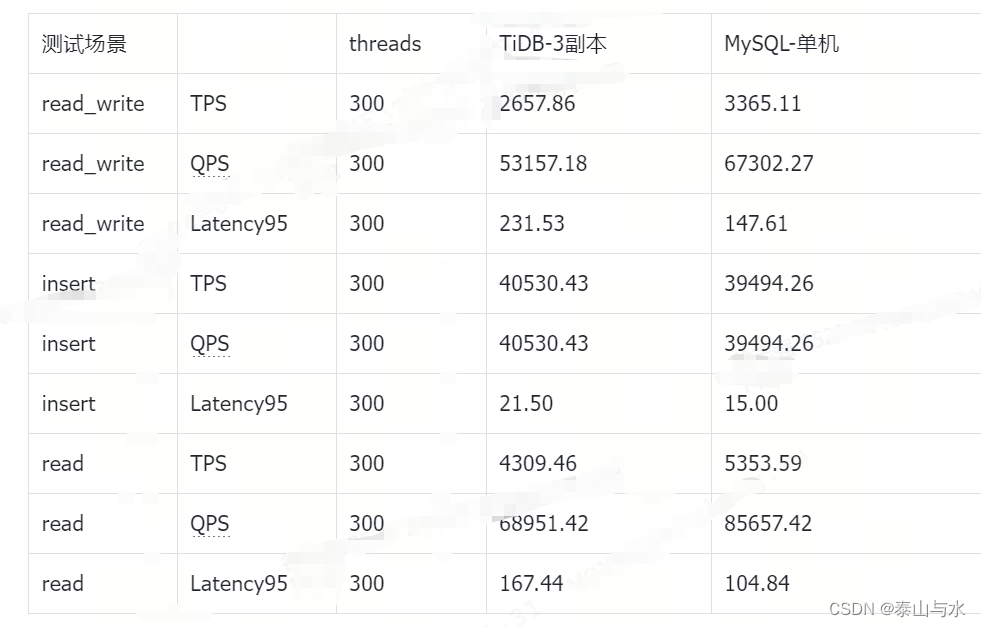
Tidb和MySQL性能简单测试对比
一、单SQL性能对比 由于TiDB的并发能力优秀,但是单个SQL执行延迟较差,为了客观对比,所以只用1个线程来压测tidb和mysql,以观察延迟情况 二、并发SQL性能对比 TiDB:v6.5.2 MySQL:8.0.26 (单机) 三、结论 …...

2024.2.6力扣每日一题——魔塔游戏
2024.2.6 题目来源我的题解方法一 贪心优先队列 题目来源 力扣每日一题;题序:LCP 30 我的题解 方法一 贪心优先队列 思路:使用贪心的思想,从左到右遍历,若遇到加上当前房间的生命值后小于等于0,由于需要…...

C# OAuth单点登录的实现
原理 单点登录(Single Sign-On,简称SSO)是一种身份验证技术,它允许用户使用一组凭据(如用户名和密码)登录多个相关但独立的系统,而无需在每个系统中都进行登录操作。下面是一个简单的SSO实现示…...

AtCoder Beginner Contest 347 (ABCDEF题)视频讲解
A - Divisible Problem Statement You are given positive integers N N N and K K K, and a sequence of length N N N, A ( A 1 , A 2 , … , A N ) A(A_1,A_2,\ldots,A_N) A(A1,A2,…,AN). Extract all elements of A A A that are multiples of K K K, divi…...
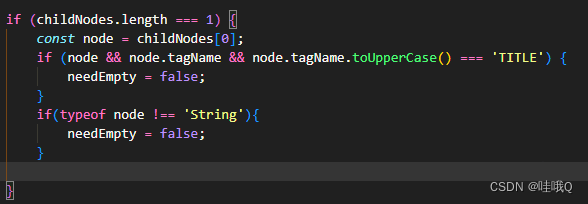
【vue2+antvx6】报错Cannot read properties of undefined (reading ‘toUpperCase‘)
我的代码是这样的 <el-collapseref"collapse"v-model"active"accordionclass"collapseStart"change"collapsechange"><el-collapse-item:name"String(index 1)"v-for"(i, index) in List":key"in…...

主流的开发语言、环境及其特点
主流的开发语言及其特点: 1. Python:以其简洁的语法和强大的库支持而闻名,适用于数据科学、人工智能和网络开发等领域。 2. Java:跨平台的编程语言,广泛应用于企业级应用、Android 开发和大型系统开发。 3. C…...

Android知识 - 代码混淆ProGuard规则介绍
ProGuard 的规则及示例 规则概述 ProGuard 是一个代码优化工具,它通过移除未使用的代码、重命名类、字段和方法等方式来减小应用的大小。在 ProGuard 的配置文件中,我们可以定义一系列的规则来控制优化和混淆的过程。 规则语法 ProGuard 的规则通常包…...

【Linux的进程篇章 - 冯诺依曼的体系结构】
Linux学习笔记---005 Linux冯诺依曼体系结构理解1、冯诺依曼体系结构1.1、冯诺依曼体系结构1.2、硬件层面1.3、数据层面1.4、那么冯诺依曼体系能干什么呢? 2、操作系统(Operastor System)2.1、概念2.2、操作系统层的核心功能 3、进程的初步理解 Linux冯诺依曼体系结…...
)
flask-(数据连接池的使用,定制命令,信号的使用,表关系的建立和查询)
文章目录 连接池实例flask定制命令flask 缓存的使用flask信号的使用sqlalchemy原生操作sqlalchemy操作表flask orm操作表一对多的增加和跨表查询 (一对一只需要关联字段加上 ,uniqueTrue)多对多关系的增加和查询多对多基本的增删改查 连接池 import pymy…...
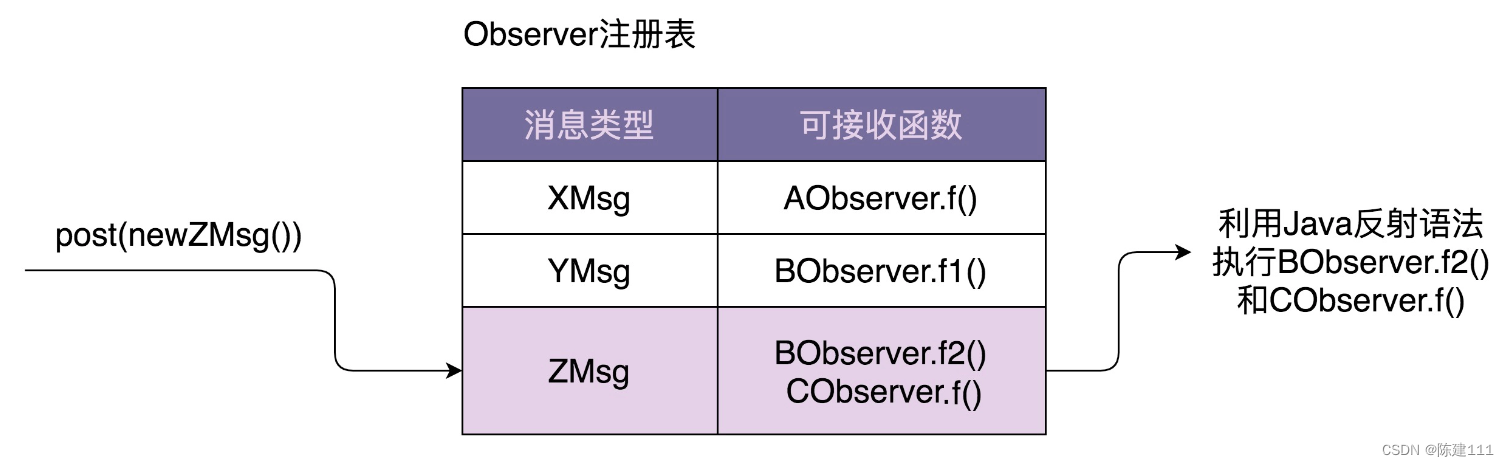
设计模式学习笔记 - 设计模式与范式 -行为型:2.观察者模式(下):实现一个异步非阻塞的EventBus框架
概述 《1.观察者模式(上)》我们学习了观察者模式的原理、实现、应用场景,重点节介绍了不同应用场景下,几种不同的实现方式,包括:同步阻塞、异步非阻塞、进程内、进程间的实现方式。 同步阻塞最经典的实现…...
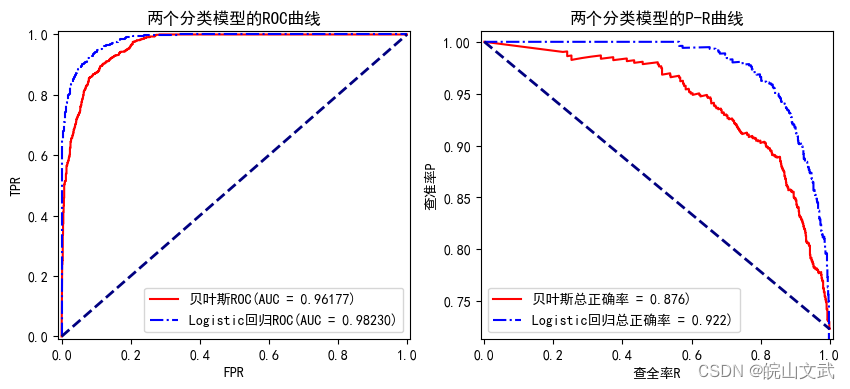
数据挖掘|贝叶斯分类器及其Python实现
分类分析|贝叶斯分类器及其Python实现 0. 分类分析概述1. Logistics回归模型2. 贝叶斯分类器2.1 贝叶斯定理2.2 朴素贝叶斯分类器2.2.1 高斯朴素贝叶斯分类器2.2.2 多项式朴素贝叶斯分类器 2.3 朴素贝叶斯分类的主要优点2.4 朴素贝叶斯分类的主要缺点 3. 贝叶斯分类器在生产中的…...
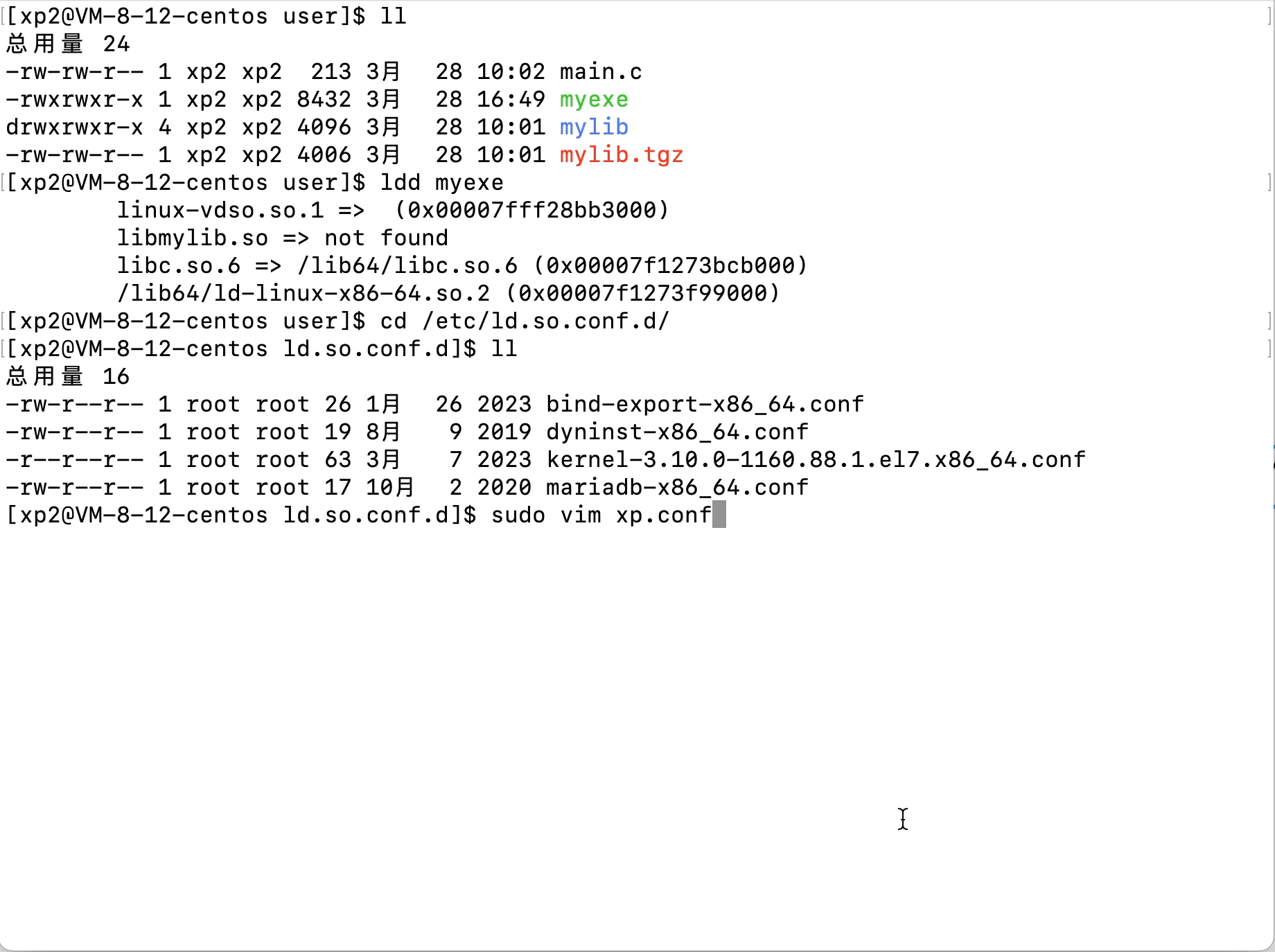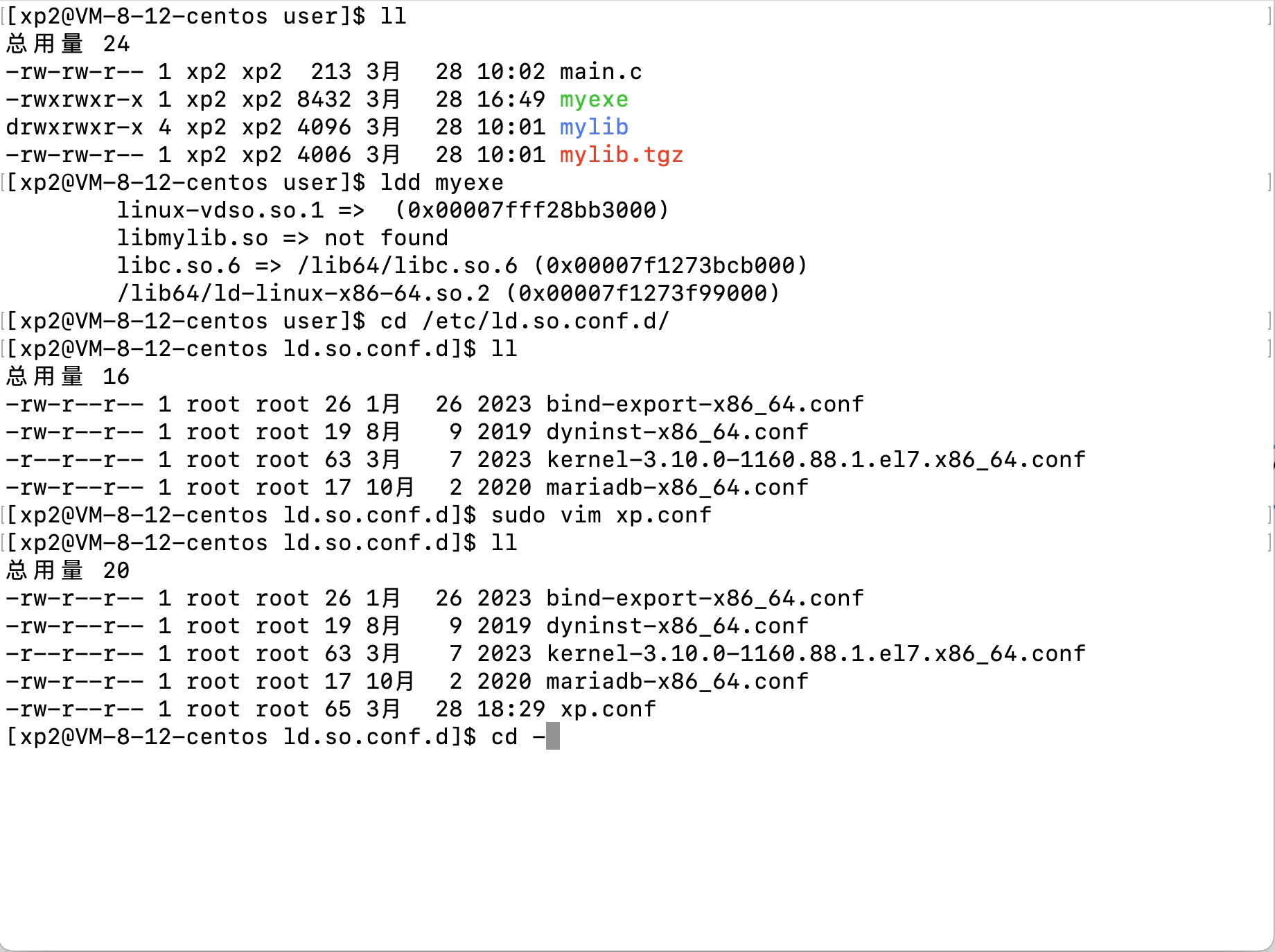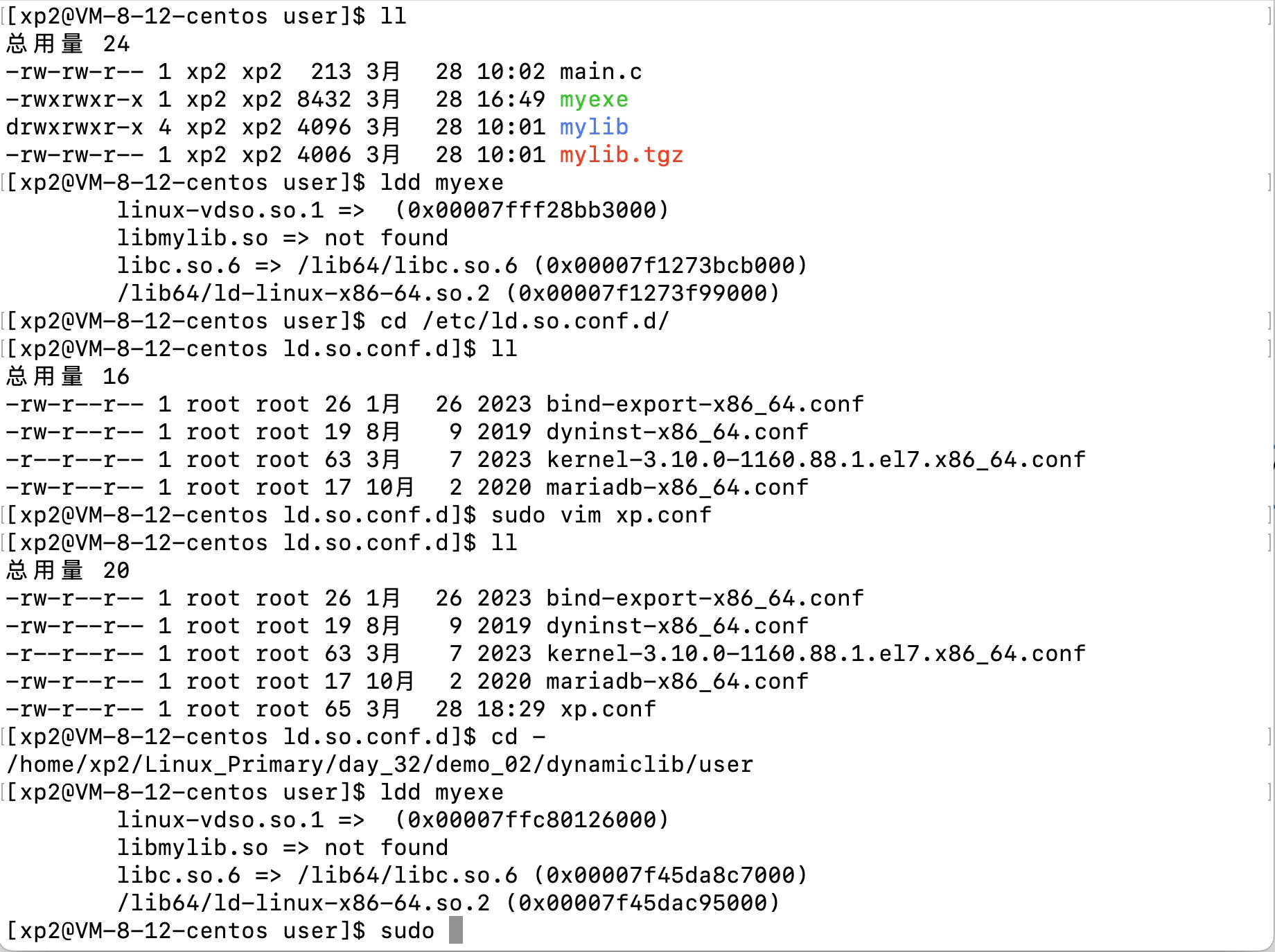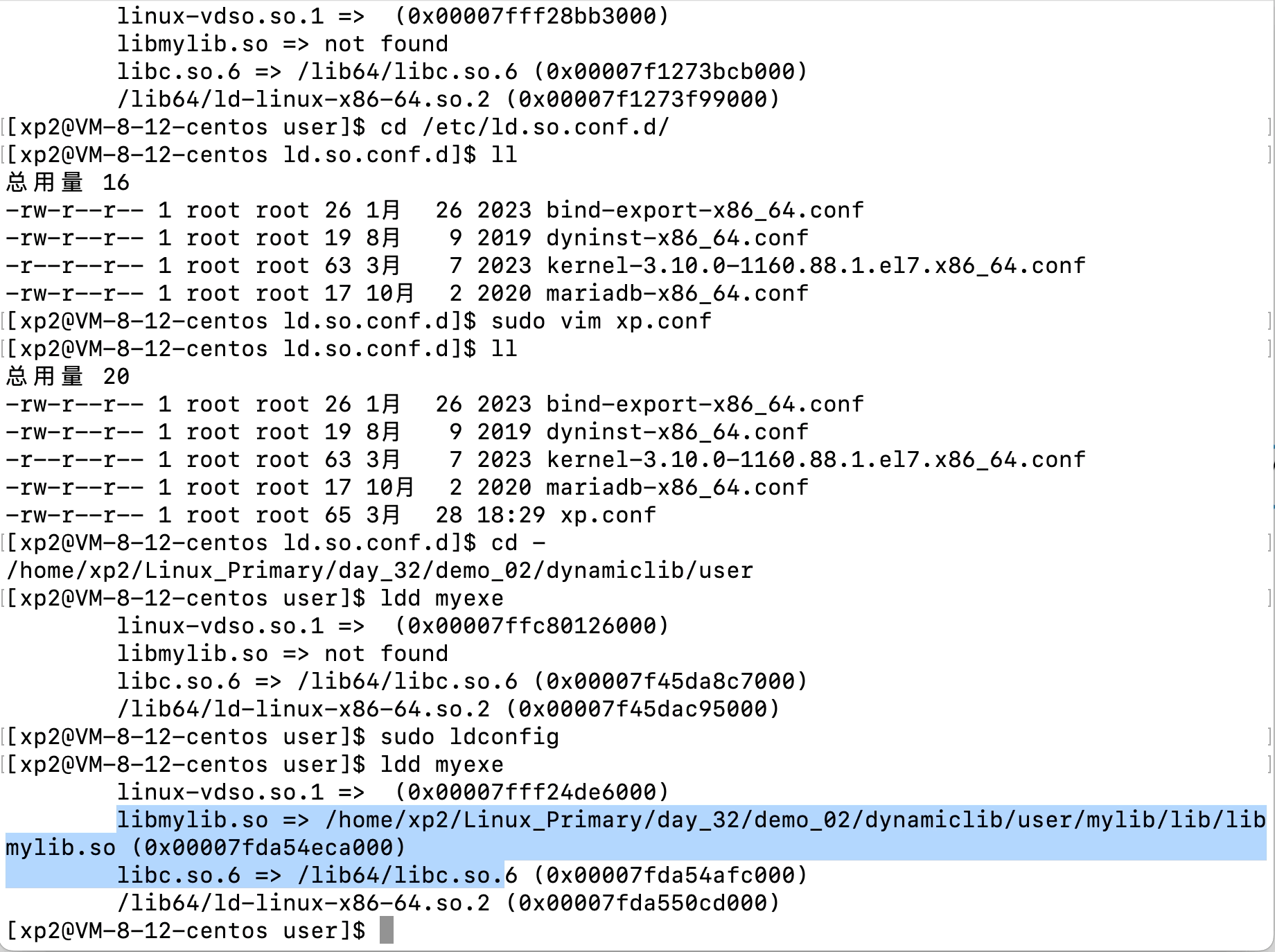
Linux文件(系统)IO(含动静态库的链接操作)
文章目录 Linux文件(系统)IO(含动静态库的链接操作)1、C语言文件IO操作2、三个数据流stdin、stdout、stderr3、系统文件IO3.1、相关系统调用接口的使用3.2、文件描述符fd3.3、文件描述符的分配规则3.3、重定向3.4、自制shell加入重…...
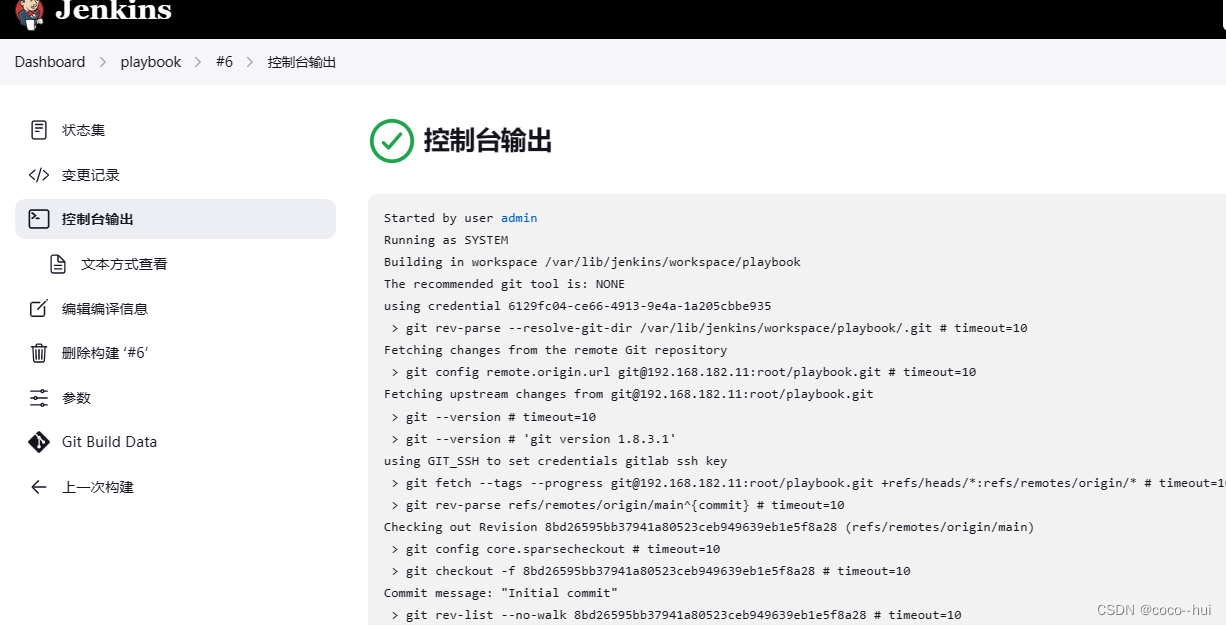
CI/CD实战-jenkins结合ansible 7
配置主机环境 在jenkins上断开并删除docker1节点 重新给master添加构建任务 将server3,server4作为测试主机,停掉其上后面的docker 在server2(jenkins)主机上安装ansible 设置jenkins用户到目标主机的免密 给测试主机创建用户并…...
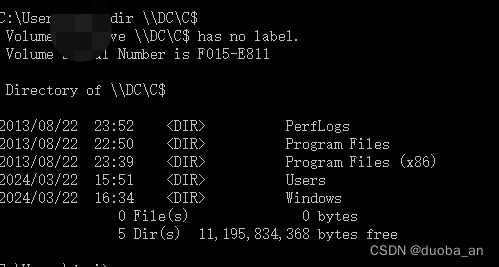
内网渗透-(黄金票据和白银票据)详解(一)
目录 一、Kerberos协议 二、下面我们来具体分析Kerberos认证流程的每个步骤: 1、KRB_AS-REQ请求包分析 PA-ENC-TIMESTAMP PA_PAC_REQUEST 2、 KRB_AS_REP回复包分析: TGT认购权证 Logon Session Key ticket 3、然后继续来讲相关的TGS的认证过程…...
学习transformer模型-Dropout的简明介绍
Dropout的定义和目的: Dropout 是一种神经网络正则化技术,它在训练时以指定的概率丢弃一个单元(以及连接)p。 这个想法是为了防止神经网络变得过于依赖特定连接的共同适应,因为这可能是过度拟合的症状。直观上&#…...
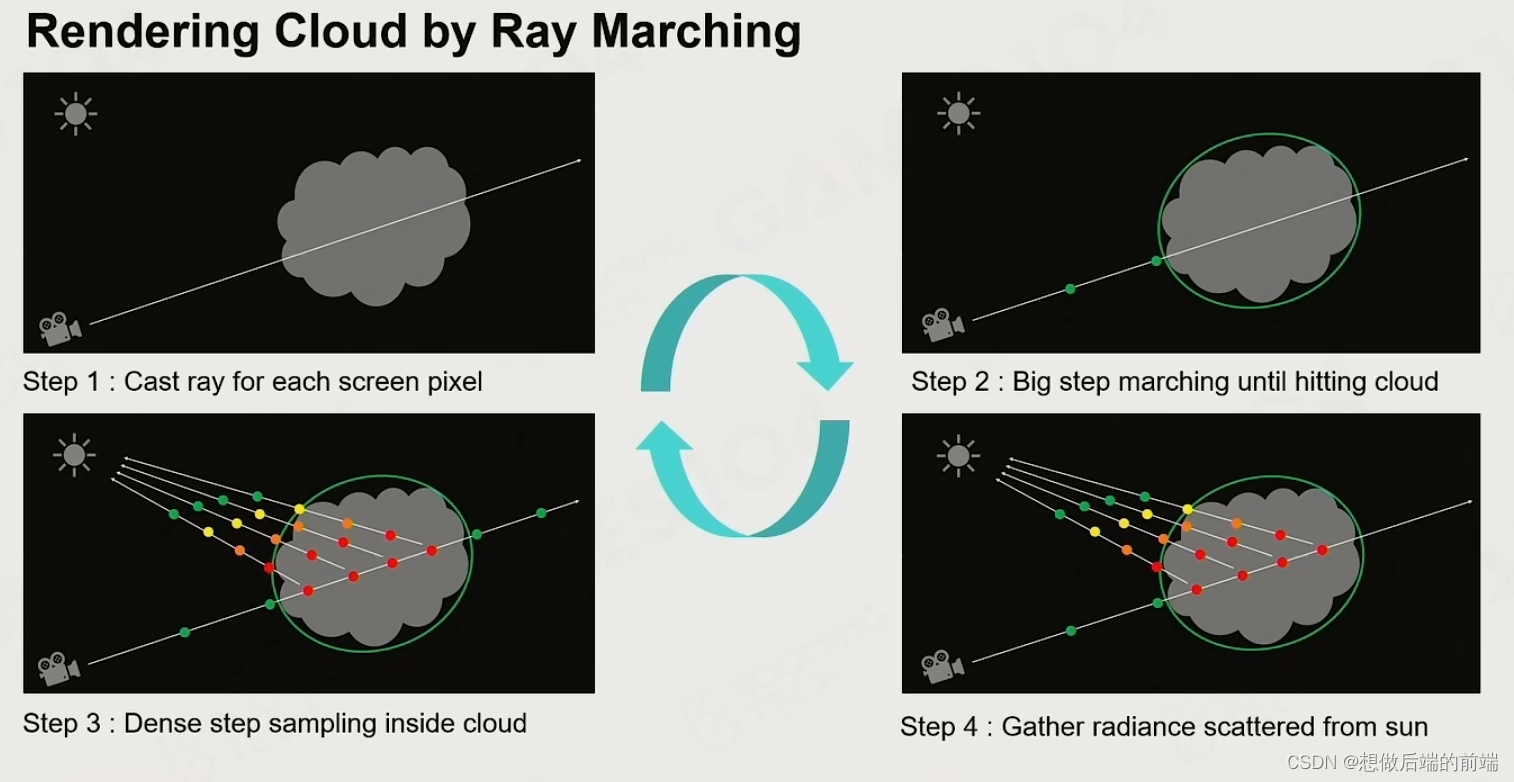
游戏引擎中的大气和云的渲染
一、大气 首先和光线追踪类似,大气渲染也有类似的渲染公式,在实际处理中也有类似 Blinn-Phong的拟合模型。关键参数是当前点到天顶的角度和到太阳的角度 二、大气散射理论 光和介质的接触: Absorption 吸收Out-scattering 散射Emission …...

华为鲲鹏云认证考试内容有哪些?华为鲲鹏云认证考试报名条件
华为鲲鹏云认证考试是华为公司为了验证IT专业人士在鲲鹏计算及云计算领域的专业能力而设立的一项认证考试。以下是关于华为鲲鹏云认证考试的一些详细信息: 考试内容:华为鲲鹏云认证考试的内容主要包括理论考核和实践考核两大部分。理论考核涉及云计算、…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
