Codeforces Round 932 (Div. 2)(A,B,C,D)
比赛链接
AB都是思维,更确切地说,A考了字符串字典序,很经典的贪心考点,B考了MEX运算。C出的还是比较好的,dp方法值得学习。D题是个不太好想的容斥,主要是变量有点多,容易搞混。
A. Entertainment in MAC
题意:
恭喜你,你被硕士援助中心录取了!但是,你在课堂上感到非常无聊,厌倦了无所事事,于是你给自己想了一个游戏。
给你一个字符串 s s s 和一个偶整数 n n n 。你可以对它进行两种运算:
- 将反向字符串 s s s 添加到字符串 s s s 的末尾(例如,如果 s = s = s= cpm,那么在执行操作后 s = s = s= cpmmpc )。
- 将当前字符串 s s s 倒转(例如,如果 s = s = s= cpm,则在执行操作后 s = s = s= mpc)。
需要确定在进行精确的 n n n 操作后,可以得到的词序最小的 † ^{\dagger} † 字符串。请注意,您可以按照任意顺序进行不同类型的运算,但必须总共进行 n n n 次运算。
† ^{\dagger} † 当且仅当以下条件之一成立时,字符串 a a a 在词法上比字符串 b b b 小:
- a a a 是 b b b 的前缀,但是 a ≠ b a \ne b a=b ;
- 在 a a a 和 b b b 不同的第一个位置上,字符串 a a a 的字母在字母表中出现的时间早于 b b b 中的相应字母。
思路:
发现新构造出来的字符串最前面 ∣ s ∣ |s| ∣s∣ 个字符要么是 s s s,要么是反向的 s s s。正向好说,不用操作就是。而要保证进行偶数次操作后,最前面是反向的 s s s,那么一定需要先用一下操作 2 2 2,再用一下操作 1 1 1。
为了字典序最小,我们后面一定是一直使用操作 2 2 2。因此我们只需要比较一下正向 s s s 和反向 s s s 哪个小,如果是正向的,那么就只用操作 2 2 2,否则先用一下操作 1 1 1,之后一直用操作 2 2 2。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;int T,n;
string s,t;int main(){cin>>T;while(T--){cin>>n>>s;t=string(s.rbegin(),s.rend());if(s<=t)cout<<s<<endl;else cout<<t+s<<endl;}return 0;
}
B. Informatics in MAC
题意:
在硕士援助中心,Nyam-Nyam 接受了一项信息学方面的家庭作业。
有一个长度为 n n n 的数组 a a a ,你想把它分成 k > 1 k\gt 1 k>1 个子段 † ^{\dagger} † ,使每个子段上的 MEX ‡ \operatorname{MEX} ^{\ddagger} MEX‡ 都等于相同的整数。
请帮助 Nyam-Nyam 找到合适的除法,或者确定不存在合适的除法。
† ^{\dagger} † 将数组划分为 k k k 个子数段的定义是 k k k 对整数 ( l 1 , r 1 ) , ( l 2 , r 2 ) , … , ( l k , r k ) (l_1, r_1), (l_2, r_2), \ldots, (l_k, r_k) (l1,r1),(l2,r2),…,(lk,rk) ,使得 l i ≤ r i l_i \le r_i li≤ri 和每个 1 ≤ j ≤ k − 1 1 \le j \le k - 1 1≤j≤k−1 , l j + 1 = r j + 1 l_{j + 1} = r_j + 1 lj+1=rj+1 ,以及 l 1 = 1 l_1 = 1 l1=1 和 r k = n r_k = n rk=n 。这些对表示子段本身。
数组中的 ‡ MEX ^{\ddagger}\operatorname{MEX} ‡MEX 是不属于该数组的最小非负整数。
例如
- 数组 [ 2 , 2 , 1 ] [2, 2, 1] [2,2,1] 的 MEX \operatorname{MEX} MEX 是 0 0 0 ,因为 0 0 0 不属于该数组。
- 数组 [ 3 , 1 , 0 , 1 ] [3, 1, 0, 1] [3,1,0,1] 中的 MEX \operatorname{MEX} MEX 是 2 2 2 ,因为 0 0 0 和 1 1 1 属于数组,而 2 2 2 不属于数组。
- 数组 [ 0 , 3 , 1 , 2 ] [0, 3, 1, 2] [0,3,1,2] 中的 MEX \operatorname{MEX} MEX 是 4 4 4 ,因为 0 0 0 、 1 1 1 、 2 2 2 和 3 3 3 属于数组,而 4 4 4 不属于数组。
思路:
每段区间都不含某个数,说明这个数在整段区间上肯定从来没出现过。所以我们要选就选在原序列中没出现的数。我们要一段区间上的 M E X MEX MEX 等于某个数 x x x,就需要这段区间上包含 1 ∼ x − 1 1\sim x-1 1∼x−1 的所有数。所以我们要每段区间的 M E X MEX MEX 值都等于某个数 x x x 的话, x x x 只可能是最小的原序列没出现的数。我们只要对这个数验证一下即可。
code:
#include <iostream>
#include <cstdio>
#include <vector>
#include <set>
using namespace std;
const int maxn=1e5+5;int T,n;
int a[maxn];int main(){cin>>T;while(T--){cin>>n;set<int> S;for(int i=1;i<=n;i++){cin>>a[i];S.insert(a[i]);}int x;for(int i=0;;i++)if(S.find(i)==S.end()){x=i;break;}vector<pair<int,int> > ans;for(int l=1,r=1,t;l<=n;){t=0;S.clear();do{S.insert(a[r++]);while(S.find(t)!=S.end())t++;if(r>n && t!=x){//将最后一段不完整的段归入到前一段l=ans.rbegin()->first;ans.pop_back();break;}
// cout<<l<<" "<<r<<endl;}while(t!=x);ans.push_back(make_pair(l,r-1));l=r;}if(ans.size()>1){cout<<ans.size()<<endl;for(auto x:ans)cout<<x.first<<" "<<x.second<<endl;}else cout<<-1<<endl;}return 0;
}
C. Messenger in MAC
题意:
凯夫特梅鲁姆硕士生援助中心的新信使计划进行一次更新,开发人员希望在更新中优化向用户显示的信息集。目前共有 n n n 条信息。每条信息由两个整数 a i a_i ai 和 b i b_i bi 表示。读取数字为 p 1 , p 2 , … , p k p_1, p_2, \ldots, p_k p1,p2,…,pk ( 1 ≤ p i ≤ n 1 \le p_i \le n 1≤pi≤n ,所有 p i p_i pi 都是不同的)的信息所花费的时间由公式计算得出:
∑ i = 1 k a p i + ∑ i = 1 k − 1 ∣ b p i − b p i + 1 ∣ \Large \sum_{i=1}^{k} a_{p_i} + \sum_{i=1}^{k - 1} |b_{p_i} - b_{p_{i+1}}| i=1∑kapi+i=1∑k−1∣bpi−bpi+1∣
请注意,读取由一个编号为 p 1 p_1 p1 的报文组成的报文集所需的时间等于 a p 1 a_{p_1} ap1 。此外,读取一组空信息所需的时间为 0 0 0 。
用户可以确定他愿意在信使中花费的时间 l l l 。信使必须告知用户信息集的最大可能大小,其阅读时间不超过 l l l 。请注意,信息集的最大大小可以等于 0 0 0 。
流行信使的开发人员未能实现这一功能,因此他们要求您解决这一问题。
思路1(堆):
上面的描述很神秘,实际上表达的意思很简单。就是可以乱序地不重复地成对选出一些 a , b a,b a,b,使得选出数的序列的 a a a 的和以及相邻两项 b b b 的差的绝对值相等。总和不超过 L L L 的前提下,使得选出的数尽可能多。
为了最小化 ∑ i = 1 k − 1 ∣ b p i − b p i + 1 ∣ \sum_{i=1}^{k - 1} | b_{p_i} - b_{p_{i+1}}| ∑i=1k−1∣bpi−bpi+1∣ 我们不妨把每对数按 b b b 来进行排序,按顺序选出若干个数后,因为有大小关系,绝对值号可以直接拆掉,前一项与后一项相消,也就是 b p k − b p k − 1 + b p k − 1 − b p k − 2 + ⋯ + b p 2 − b p 1 b_{p_k}-b_{p_{k-1}}+b_{p_{k-1}}-b_{p_{k-2}}+\dots+b_{p_{2}}-b_{p_{1}} bpk−bpk−1+bpk−1−bpk−2+⋯+bp2−bp1 那么它就变成了 b p k − b p 1 b_{p_k}-b_{p_{1}} bpk−bp1。把 p 1 p_1 p1 看成选取区间的左端点, p k p_k pk 看成右端点的话,则原式就相当于在区间 [ l , r ] [l,r] [l,r] 中选取若干个数,使得 a i a_i ai 之和加上 r − l r-l r−l 小于等于 L L L(左右端点必选),问最多能选多少个数。
朴素的想法是先枚举右端点,然后枚举左端点,然后贪心地选区间内最小的前几个数。但是这样最坏是 O ( n 3 l o g n ) O(n^3log\,n) O(n3logn) 的(区间排序占 O ( n l o g n ) O(nlog\,n) O(nlogn))。我们希望有个 O ( n 2 l o g n ) O(n^2log\,n) O(n2logn) 的做法。所以我们考虑能否从上一个区间直接推过来。
一个想法是:枚举右端点 r r r,然后左端点 l l l 从 r r r 向 1 1 1 推。使用堆来存储区间 [ l , r ] [l,r] [l,r] 中最小的若干个值,使得它们的和 ≤ L − ( r − l ) \le L-(r-l) ≤L−(r−l)(这意味着我们以 l , r l,r l,r 为左右端点的时候,选取的就是堆中的数,因为总和满足前面的条件,因此在值上是满足条件的)。
不过这个想法有个比较明显的缺陷,就是有可能我们推到某个左端点 l l l 根本没选 a l a_l al,而是直接将它踢出了堆,这样就不符合左右端点必选的条件了。不过这样还是可以得到正确答案的,因为这种不符合条件的情况一定无法更新答案。
为什么呢?假设我们推到了某个左端点 l l l 却没有选上 a l a_l al,那么我们此时堆中最靠左的数的位置 l ′ l' l′ 作为左端点时,堆中数的总和加上 r − l ′ r-l' r−l′ 一定更小,比这个情况更有可能更新答案。前面的情况已经更新过答案了,因此这个情况一定无法更新答案。这就保证了正确性。
code:
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=2005;int T,n;
ll L;
pair<int,int> x[maxn];int main(){cin>>T;while(T--){cin>>n>>L;for(int i=1;i<=n;i++){cin>>x[i].second>>x[i].first;}sort(x+1,x+n+1);int ans=0;for(int r=1;r<=n;r++){priority_queue<int> h;ll tot=0;for(int l=r;l>=1;l--){h.push(x[l].second);tot+=x[l].second;while(tot+x[r].first-x[l].first>L && !h.empty()){tot-=h.top();h.pop();}if(tot+x[r].first-x[l].first<=L)ans=max(ans,(int)h.size());}}cout<<ans<<endl;}return 0;
}
思路2(动态规划):
我们在选数的时候需要知道那些数是第一个选上的数,哪一个是最后一个选上的数,所以设 d p 1 [ i ] [ j ] dp1[i][j] dp1[i][j] 表示前 i i i 个数中选出 j j j 的最小值, d p 2 [ i ] [ j ] dp2[i][j] dp2[i][j] 表示前 i i i 个数中选出 j j j 个,并且最后一个数选 a j a_j aj 的最小值。
d p 1 dp1 dp1 我们就正常选数即可,只需要特判一下当前状态选择的是否是第一个数, d p 2 dp2 dp2 由 d p 1 dp1 dp1 来推,这样 d p 2 dp2 dp2 得到的就是一种选取方式,即若干个 a a a 的值减去 b l b_l bl 再加上 b r b_r br。
而第一维为 i i i 的 d p 1 , d p 2 dp1,dp2 dp1,dp2 之和 i − 1 i-1 i−1 的有关,所以我们可以优化掉第一维。这样就变成了 jiangly 大佬的写法了。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <set>
using namespace std;
typedef long long ll;
const ll inf=1e18;
const int maxn=2005;int T,n;
ll l;
pair<int,int> itv[maxn];int main(){cin>>T;while(T--){cin>>n>>l;for(int i=1;i<=n;i++)cin>>itv[i].second>>itv[i].first;sort(itv+1,itv+n+1);vector<ll> dp1(n+1,inf),dp2(n+1,inf);for(int i=1;i<=n;i++){ll a=itv[i].second;ll b=itv[i].first;for(int j=n;j>=1;j--){dp1[j]=min(dp1[j],dp1[j-1]+a);dp2[j]=min(dp2[j],dp1[j-1]+a+b);}dp1[1]=min(dp1[1],a-b);dp2[1]=min(dp2[1],a);}for(int i=n;i>=1;i--){if(dp2[i]<=l){cout<<i<<endl;break;}if(i==1){cout<<0<<endl;}}}return 0;
}
D. Exam in MAC
题意:
硕士生援助中心公布了入学考试,考试内容如下。
给考生一个大小为 n n n 的集合 s s s 和一个奇怪的整数 c c c 。对于这个集合,需要计算出使 0 ≤ x ≤ y ≤ c 0 \leq x \leq y \leq c 0≤x≤y≤c , x + y x + y x+y 不包含在集合 s s s 中,并且 y − x y - x y−x 也不包含在集合 s s s 中, ( x , y ) (x, y) (x,y) 对的个数。
你的朋友想进入中心工作。请帮助他通过考试!
思路:
容斥原理。很好的题。
x , y x,y x,y 是任取的,我们当然不可能任取,用屁股想都会超时。因此从 x + y , y − x x+y,y-x x+y,y−x 下手。假设 x + y = a ∉ s , y − x = b ∉ s x+y=a\not\in s,y-x=b\not\in s x+y=a∈s,y−x=b∈s,则有 x = a − b 2 , y = a + b 2 x=\dfrac{a-b}2,y=\dfrac{a+b}2 x=2a−b,y=2a+b。显然 b ≤ a b\le a b≤a,并且当 a , b a,b a,b 不同时,得到的 x , y x,y x,y 一定不同(也就说有多少对不同的 a , b a,b a,b,就有多少对不同的 x , y x,y x,y)。
题目说 x + y , y − x x+y,y-x x+y,y−x 不在集合 s s s 中,也就是 a , b a,b a,b 不在集合 s s s 中。我们只要找到所有不在集合 s s s 中的数,让 a , b a,b a,b 去等于这些数,就能得到一对对 x , y x,y x,y。但是问题在于如何保证得到的 x , y x,y x,y 合法,以及如何计数。
一开始的想法是因为 a − b 2 ≤ a + b 2 ≤ c \dfrac{a-b}2\le \dfrac{a+b}2 \le c 2a−b≤2a+b≤c,所以枚举 a a a,然后去算 b b b 的个数,不过还是太麻烦了,当 c c c 很大的时候还需要将一整段进行压缩,整段求和,暴力来算会T。
所以尝试反着来求。用总的对数减去 a a a(也就是 x + y x+y x+y) 合法的对数和 b b b(也就是 y − x y-x y−x) 合法的对数,最后再加上 a , b a,b a,b 同时合法的对数,剩下的就是不合法的对数。
-
总对数显然是 C c + 1 2 = ( c + 1 ) ∗ ( c + 2 ) / 2 C_{c+1}^2=(c+1)*(c+2)/2 Cc+12=(c+1)∗(c+2)/2。( x , y x,y x,y 可选 0 ∼ c 0\sim c 0∼c 的数,包括 0 0 0)
-
我们让 a a a 去等于已有的数,得到的就是 a a a 合法的对数。假设这个数是 t t t,那么 x + y = t x+y=t x+y=t ,又因为 y ≥ x y\ge x y≥x,所以得到的总的合法对数为 t / 2 + 1 t/2+1 t/2+1。
-
同理,我们让 b b b 去等于已有的数,得到的就是 b b b 合法的对数。假设这个数是 t t t,那么 y − x = t y-x=t y−x=t ,因为 y ≤ t y\le t y≤t,所以得到的总的合法对数为 c − t + 1 c-t+1 c−t+1。
-
a , b a,b a,b 同时合法的话,需要 x = a − b 2 , y = a + b 2 x=\dfrac{a-b}2,y=\dfrac{a+b}2 x=2a−b,y=2a+b 算出来的 x , y x,y x,y 为正整数,因此 a , b a,b a,b 需要奇偶性相同。我们统计一下给出的数中有多少个奇数 o o o 和偶数 e e e,总数就是 C e 2 + C o 2 = e ∗ ( e + 1 ) / 2 + o ∗ ( o + 1 ) / 2 C_e^2+C_o^2=e*(e+1)/2+o*(o+1)/2 Ce2+Co2=e∗(e+1)/2+o∗(o+1)/2。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;int T,n,c;int main(){cin>>T;while(T--){cin>>n>>c;ll ans=1ll*(c+1)*(c+2)/2;int o=0,e=0;for(int i=1,t;i<=n;i++){cin>>t;ans-=t/2+1;//x+y=tans-=c-t+1;//y-x=tif(t&1)o++;else e++;}ans+=1ll*o*(o+1)/2;ans+=1ll*e*(e+1)/2;cout<<ans<<endl;}return 0;
}
相关文章:
(A,B,C,D))
Codeforces Round 932 (Div. 2)(A,B,C,D)
比赛链接 AB都是思维,更确切地说,A考了字符串字典序,很经典的贪心考点,B考了MEX运算。C出的还是比较好的,dp方法值得学习。D题是个不太好想的容斥,主要是变量有点多,容易搞混。 A. Entertainme…...
初识C++ · 入门(2)
目录 1 引用 1.1引用的概念 1.2 引用的特性 2 传值,传引用的效率 3 引用和指针的区别 4 内联函数 4.1 内联函数的定义 4. 2 内联函数的特性 5 关键字auto 5.1关于命名的思考 5.2 关于auto的发展 5.3 auto使用规则 6 范围for的使用 7 空指针 1 引用 …...
【opencv】教程代码 —ShapeDescriptors
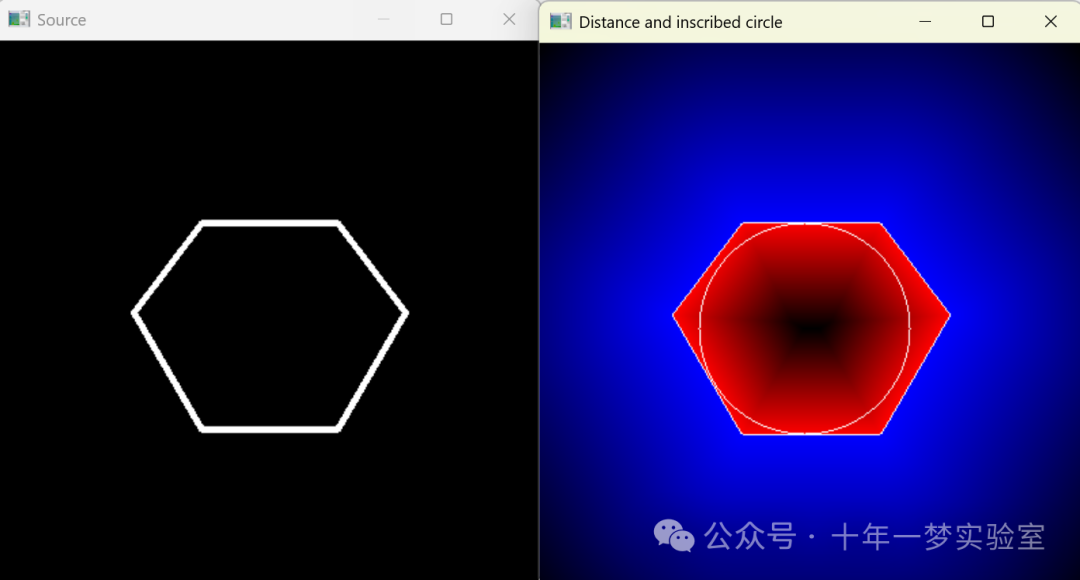
检测和显示图像的轮廓 在图像中搜索并显示轮廓边缘多边形、轮廓矩形和包围圆 获取包含检测到的轮廓的椭圆和旋转的矩形 图像轮廓检测和轮廓凸包 计算图像中的轮廓的矩(包括面积、重心等)并进行显示 创建和绘制一个多边形图像然后计算并显示图像上每个点到…...

2024-03-28 Java8之Collectors类
Collectors类常用方法 文章目录 Collectors类常用方法1.toList、toSet、toMap2.joining、counting、summingInt、minBy3.groupingBy 1.toList、toSet、toMap Collector<T, ?, List<T>> toList(); //收集为List集合 Collector<T, ?, Set<T>> toSet()…...
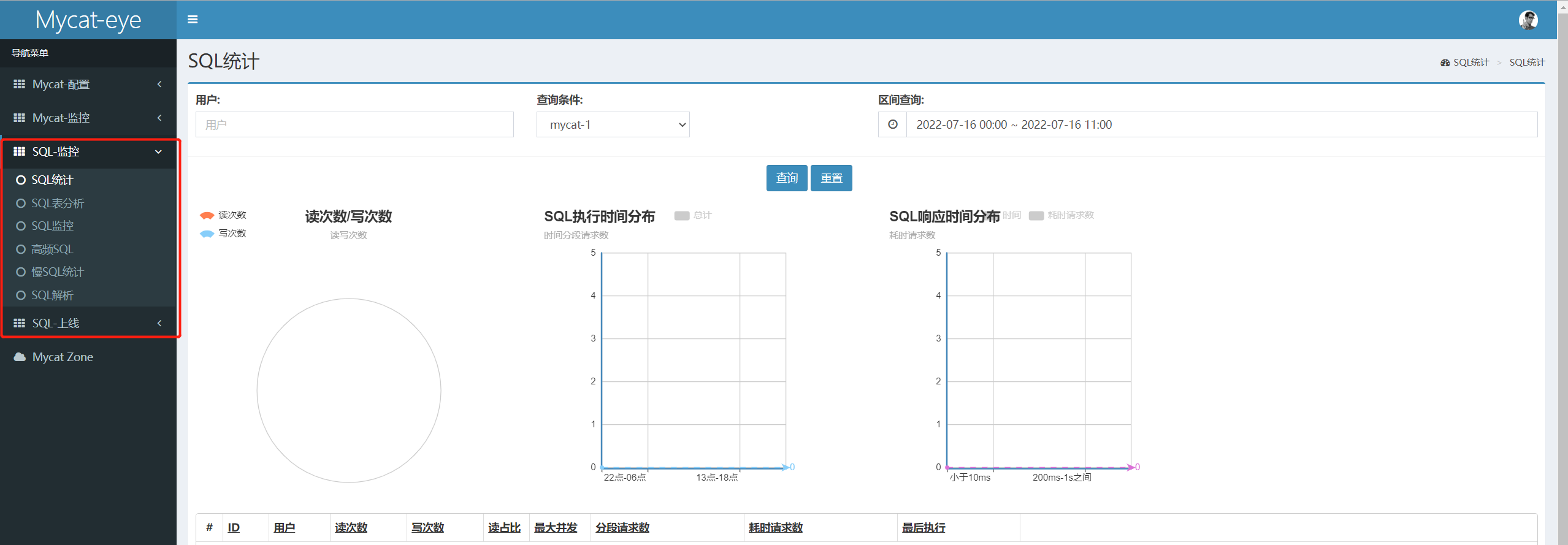
第116讲:使用Mycat-eye管理Mycat数据库服务
文章目录 1.Mycat的管理工具2.Mycat-eye介绍3.部署Mycat-eye3.1.安装Zookeep3.2.安装Mycat-eye3.3.访问Mycat-eye 4.在Mycat-eye中导入Mycat服务的信息 1.Mycat的管理工具 Mycat默认开通2个端口,可以在server.xml中进行修改。 8066 数据访问端口,即进行…...

XR虚拟直播间,引领创新风潮,打破直播局限!
随着互联网技术日新月异的发展,直播行业也迎来了蓬勃发展的春天。然而,大多数直播间在吸引观众眼球和延长用户观看时长方面,仍然面临着巨大的挑战。正是在这样的背景下,XR虚拟直播系统应运而生,以其多维度的直播场景、…...
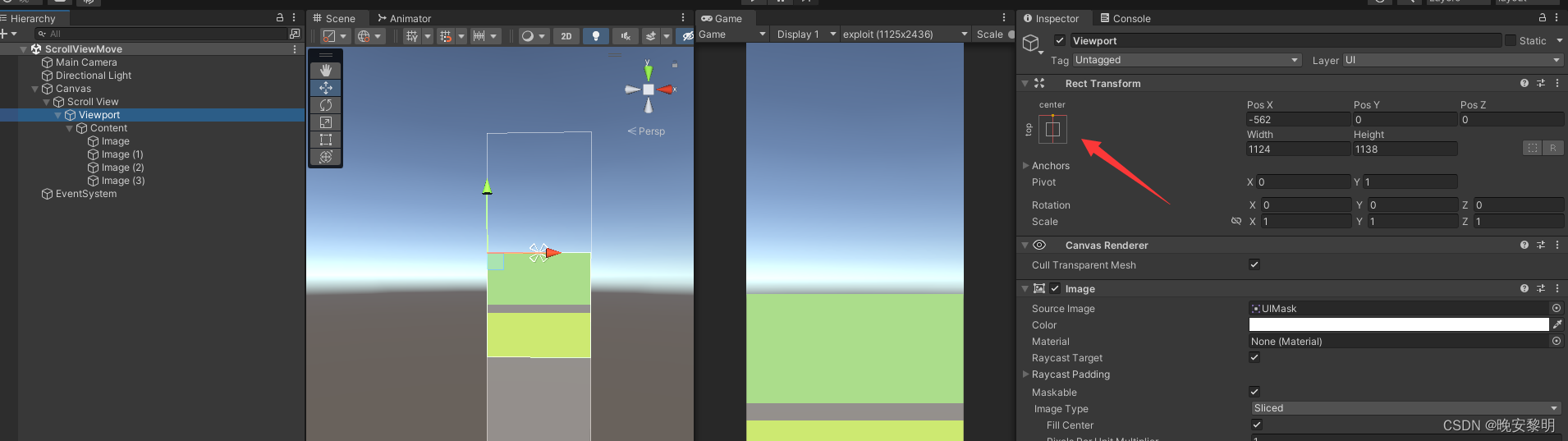
unity双层滑动实现
实现功能: 当滑动列表中内容处于顶端的时候,向上滑动优先滑动整个滑动列表,当滑动列表移动到设置位置,即设定的最高处时,继续移动列表内内容。向下移动亦然,当内容处于滑动列表顶端时,移动整个滑…...

浅谈AI技术创业有哪些机会?
一、AI技术创业概念简介 AI技术创业指的是利用人工智能(Artificial Intelligence,AI)技术进行创业活动。人工智能是指计算机系统能够模拟和展现出人类智能的一种技术。在AI技术创业中,创业者利用AI技术来解决现实生活中的问题&…...
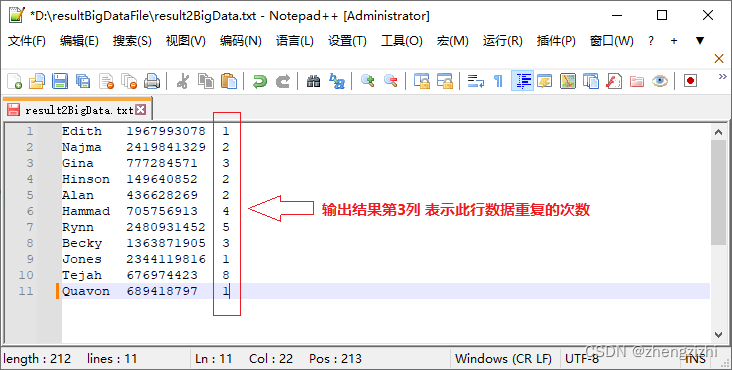
大数据-TXT文本重复行计数工具
支持系统类型:Windows 64位系统 Linux 64位系统 苹果64位系统 硬盘要求:固态硬盘(有效剩余磁盘空间大小最低3倍于大数据文件的大小) 内存要求:最低8G(例如只有几百G数据) 如果处理TB级大数据文…...

【无标题】331
2024年3月31日19:26:09 和一个好感度为40的女生完成了一次基础的对话 2024年3月31日19:26:26 在群里完成了一个毫无所谓的对话 2024年3月31日19:40:04开始准备写论文了 2024年3月31日19:40:11好感度为40的女生回复了我本质上是回复率只有40的人回复了我那应该感到高兴才对 …...
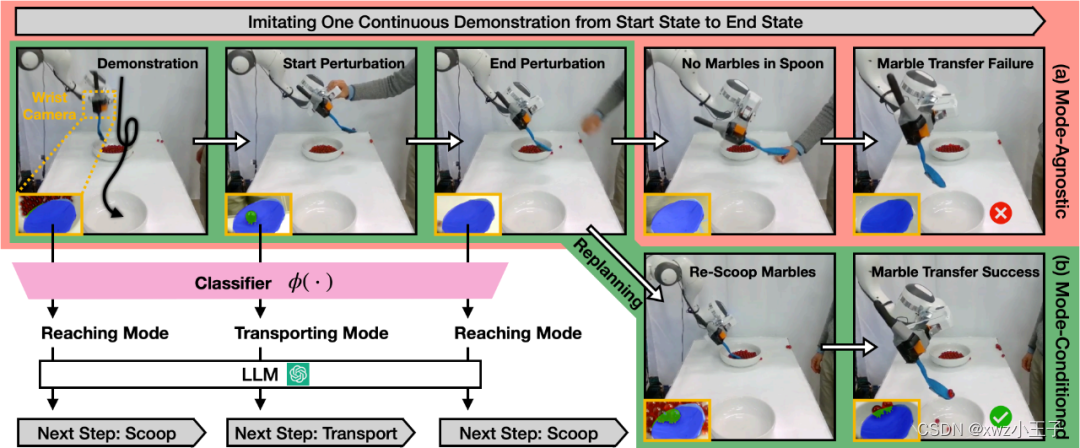
MIT最新研究成果 机器人能够从错误中纠偏 无需编程介入和重复演示
目前科学家们正在努力让机器人变得更加智能,教会他们完成诸如擦拭桌面,端盘子等复杂技能。以往机器人要在非结构化环境执行这样的任务,需要依靠固定编程进行,缺乏场景通用性,而现在机器人的学习过程主要在于模仿&#…...

C语言—指针数组
从键盘任意输入一个整型表示的月份值,用指针数组编程输出该月份的英文表示,若输入的月份值不在1~12之间,则输出“Illegal month”。 **输入格式要求:"%d" 提示信息:"Input month number:&q…...

OpenCV图像二值化
1.二值图像 灰度图像 0 - 255二值图像 0(黑) / 255(白) 2.二值分割 五种阈值分割方法(阈值T): 大于T为255,小于T为0 大于T为0,小于T为255 小于T为原值 else T 小于…...

java中的抽象类
抽象类是指包含了抽象方法的类。在java中,抽象方法指的是用abstract关键字进行修饰的方法,抽象方法与普通的方法的最大区别就是抽象方法没有方法体,也就是说抽象方法是没有具体的实现的。这也就意味着在抽象类的子类中调用抽象方法时…...

代码随想录算法训练营第二十天| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
系列文章目录 目录 系列文章目录654.最大二叉树递归法[左闭右开)[左闭右闭] 617.合并二叉树递归法(前中后序都可,以前序为例)迭代法(类似 101. 对称二叉树 写法,可用双端队列/单端队列<栈>,以单端队列…...

2014年认证杯SPSSPRO杯数学建模A题(第二阶段)轮胎的花纹全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 A题 轮胎的花纹 原题再现: 轮胎被广泛使用在多种陆地交通工具上。根据性能的需要,轮胎表面常会加工出不同形状的花纹。在设计轮胎时,往往要针对其使用环境,设计出相应的花纹形状。 第二阶段问…...
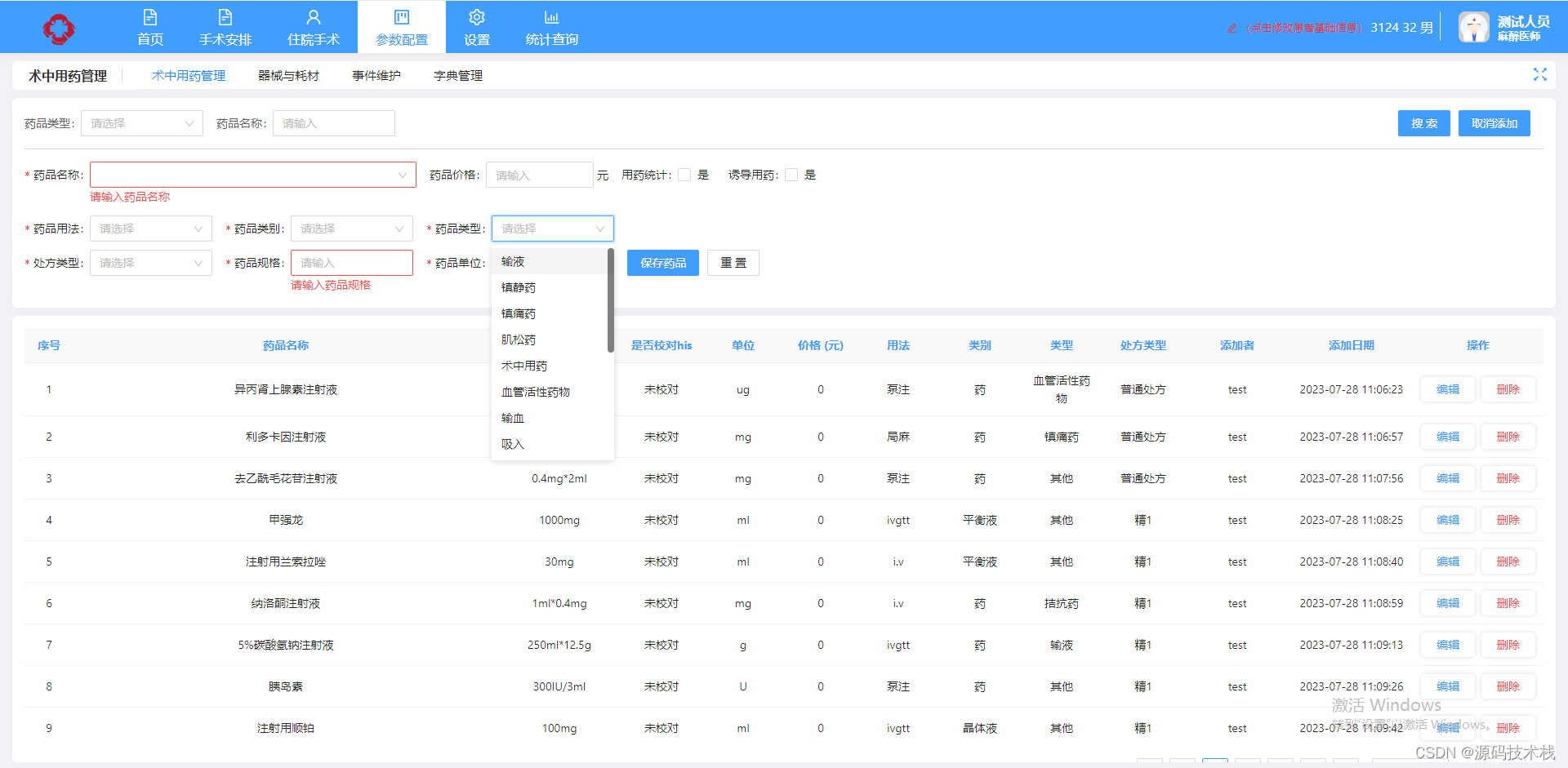
C#全新一代医院手术麻醉系统围术期全流程源码
目录 一、麻醉学科的起源 二、麻醉前访视与评估记录单 患者基本信息 临床诊断 患者重要器官功能及疾病情况 病人体格情况分级 手术麻醉风险评估 拟施麻醉方法及辅助措施 其他需要说明的情况 访视麻醉医师签名 访视时间 与麻醉相关的检查结果 三、手术麻醉信息系统…...

Python 神器:一键下载 M3U8 并转换为 MP4
在这个数字时代,我们经常在网页上遇到各种精彩的视频,但往往只能观看而无法下载。今天,我将向大家介绍如何使用 Python 自动下载网页中的 M3U8 链接,并将其转换为 MP4 格式,让你轻松保存喜欢的视频! 一、准…...
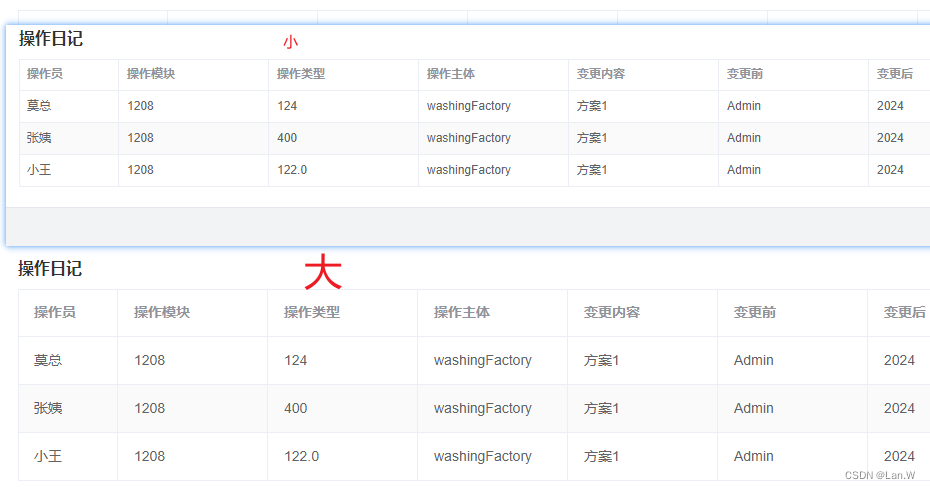
vue3全局控制Element plus所有组件的文字大小
项目框架vue-右上角有控制全文的文字大小 实现: 只能控制element组件的文字及输入框等大小变化,如果是自行添加div,text, span之类的控制不了。 配置流程 APP.vue 使用element的provide,包含app <el-config-provider :locale"loca…...
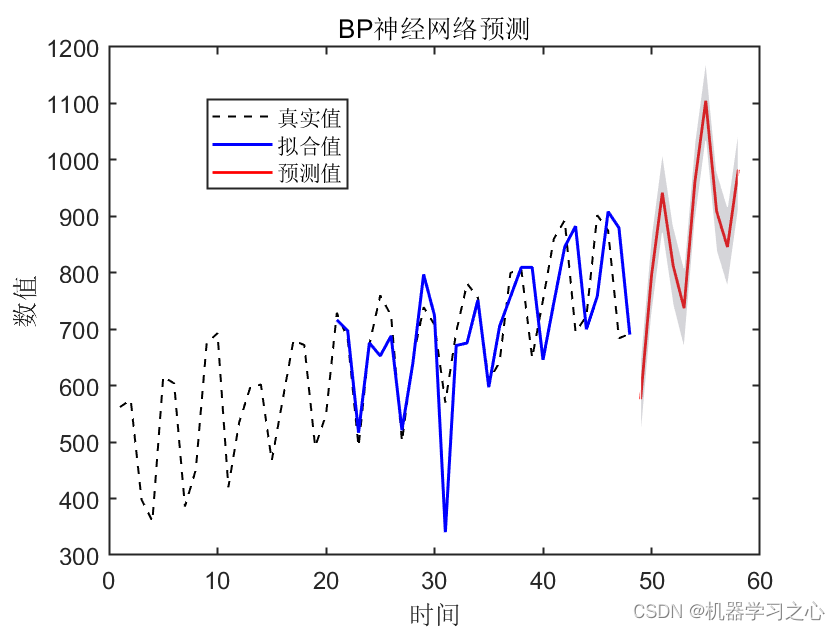
区间预测 | Matlab实现带有置信区间的BP神经网络时间序列未来趋势预测
区间预测 | Matlab实现带有置信区间的BP神经网络时间序列未来趋势预测 目录 区间预测 | Matlab实现带有置信区间的BP神经网络时间序列未来趋势预测预测效果基本介绍研究回顾程序设计参考资料预测效果 基本介绍 BP神经网络(Backpropagation neural network)是一种常用的人工神…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
