代码随想录算法训练营第二十天| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
系列文章目录
目录
- 系列文章目录
- 654.最大二叉树
- 递归法
- [左闭右开)
- [左闭右闭]
- 617.合并二叉树
- 递归法(前中后序都可,以前序为例)
- 迭代法(类似 101. 对称二叉树 写法,可用双端队列/单端队列<栈>,以单端队列为例)
- 700.二叉搜索树中的搜索
- ①递归法(没有涉及到前中后序,因为二叉树的顺序性已经帮我们确定了我们的遍历顺序)
- ②迭代法
- 普通二叉树迭代
- 利用二叉搜索树特点,自己使用了栈/队列(麻烦多此一举)
- 利用二叉搜索树特点,优化,可以不需要栈
- 98.验证二叉搜索树
- ①暴力解法 有效的二叉搜索树的中序遍历数组为升序数组(递归+for循环)
- ②递归法 中序遍历二叉树过程中检测是否升序
- ③迭代法(中序遍历)
- 统一迭代
- 普通迭代(借助指针访问节点,栈处理元素)
654.最大二叉树
凡是涉及到构造二叉树的题目都要用前序遍历(中左右),先构造根节点然后才能递归去构造左右子树。与 106.从中序与后序遍历序列构造二叉树 和 105.从前序与中序遍历序列构造二叉树 相似。注意索引分割。
递归法
[左闭右开)
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMaximumBinaryTree1(nums, 0, nums.length);}public TreeNode constructMaximumBinaryTree1(int[] nums, int begin, int end) {if (begin >= end) {return null;}//中(找到根节点并构建节点)int maxIndex = begin;//先初始最大节点为开始节点int maxVal = nums[maxIndex];for (int i = begin + 1; i < end; i++) {//从第二个节点开始在区间上遍历找最大节点if (nums[i] > maxVal) {maxVal = nums[i];maxIndex = i;//最大值下标}}TreeNode root = new TreeNode(nums[maxIndex]);//构造节点root.left = constructMaximumBinaryTree1(nums, begin, maxIndex);//左root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, end);//右return root;}
}
[左闭右闭]
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMaximumBinaryTree1(nums, 0, nums.length - 1);}public TreeNode constructMaximumBinaryTree1(int[] nums, int begin, int end) {//终止条件if (begin > end) {return null;}//中int maxIndex = begin;int maxVal = nums[maxIndex];for (int i = begin + 1; i <= end; i++) {if (nums[i] > maxVal) {maxIndex = i;maxVal = nums[maxIndex];}}TreeNode root = new TreeNode(maxVal);//构造节点root.left = constructMaximumBinaryTree1(nums, begin, maxIndex - 1);root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, end);return root;}
}
617.合并二叉树
同时遍历就同时判断两个树的情况,改变其中一棵树的结构来当做需要生成的新的数。
递归法(前中后序都可,以前序为例)
终止条件:如果其中一个二叉树的根节点为null,则不需要覆盖,直接用另一个二叉树返回就行。如果都是null,第一个if中root1 = null,会自动返回root2的null。
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {//终止条件// 如果其中一个二叉树的根节点为null,则不需要覆盖,直接用另一个二叉树返回就行// 如果都是null,第一个if中root1 = null,会自动返回root2的nullif (root1 == null) return root2;if (root2 == null) return root1;//重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。root1.val = root1.val + root2.val; // 中root1.left = mergeTrees(root1.left,root2.left); //左root1.right = mergeTrees(root1.right,root2.right); //右return root1;}
}
迭代法(类似 101. 对称二叉树 写法,可用双端队列/单端队列<栈>,以单端队列为例)
通过队列成对存放两个树的节点即可。
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if (root1 == null) return root2;if (root2 == null) return root1;Queue<TreeNode> que = new LinkedList<>();que.add(root1);que.add(root2);while (!que.isEmpty()) {TreeNode node1 = que.poll();TreeNode node2 = que.poll();node1.val = node1.val + node2.val;if (node1.left != null && node2.left != null) {que.add(node1.left);que.add(node2.left);} else if (node2.left != null) {node1.left = node2.left;}if (node1.right != null && node2.right != null){que.add(node1.right);que.add(node2.right);}else if(node2.right != null){node1.right = node2.right;}}return root1;}
}
700.二叉搜索树中的搜索
①递归法(没有涉及到前中后序,因为二叉树的顺序性已经帮我们确定了我们的遍历顺序)
递归三部曲:
-
确定递归函数的参数和返回值:递归函数的参数传入的就是根节点和要搜索的数值,返回的就是以这个搜索数值所在的节点。
-
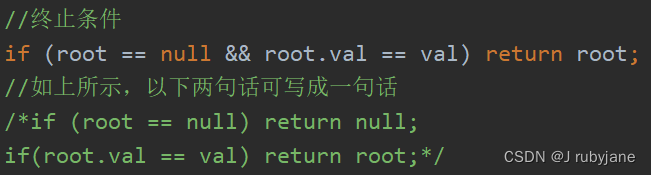
确定终止条件:如果
root为空,或者找到这个数值了,就返回root节点。
-
确定单层递归的逻辑:
TreeNode result = null;初始化递归返回结果,默认值为null。- 如果当前节点的
val大于目标val,证明val只可能出现在当前节点的左子树中,返回左子树的搜索结果result。 - 如果当前节点的
val小于目标val,证明val只可能出现在当前节点的右子树中,返回右子树的搜索结果result。
class Solution {public TreeNode searchBST(TreeNode root, int val) {//终止条件if (root == null || root.val == val) return root;//如上所示,以下两句话可写成一句话/*if (root == null) return null;if(root.val == val) return root;*///其实这个也可以不写,如果不写不影响结果,但就会让递归多进行了一层。/*if (root.left == null && root.right == null && root.val != val) return null*/TreeNode result = null;//递归返回结果,默认值为nullif (root.val > val) {result = searchBST(root.left, val);//向左搜索}if (root.val < val) {result = searchBST(root.right, val);//向右搜索}return result;//如果左右都搜索不到,则返回null。}
}
②迭代法
普通二叉树迭代
class Solution {public TreeNode searchBST(TreeNode root, int val) {if(root == null||root.val==val) return root;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();//if(node!=null){if(node.val==val)return node;if(node.left!=null)stack.push(node.left);//空节点不入栈if(node.right!=null)stack.push(node.right);//}}return null;}
}
利用二叉搜索树特点,自己使用了栈/队列(麻烦多此一举)
import java.util.LinkedList;
import java.util.Queue;
class Solution {public TreeNode searchBST(TreeNode root, int val) {Queue<TreeNode> que = new LinkedList<>();if (root == null || root.val == val) return root;TreeNode node = null;que.add(root);while (!que.isEmpty()) {node = que.poll();if (node == null || node.val == val) break;if (node.val > val) {que.add(node.left);}if (node.val < val) {que.add(node.right);}}return node;}
}
利用二叉搜索树特点,优化,可以不需要栈
注:向左向右遍历时必须使用 else if,因如果满足代码中的①,则 root 值已经改变,如果直接使用 if,则会用改变的root值(假设为null)去判断是否成立,此时会报空指针异常!
class Solution {public TreeNode searchBST(TreeNode root, int val) {while (root != null) {if (root.val == val) return root;if (root.val > val) root = root.left;//①else if (root.val < val) root = root.right;//此处 必须使用 else if,因如果满足①,则 root 值已经改变,// 如果直接使用 if,则会用改变的root值(假设为null)去判断是否成立,// 此时会报空指针异常!/* if (root.val > val) root = root.left;else if (root.val < val) root = root.right;else return root;*/}return null;}
}
98.验证二叉搜索树
这道题目比较容易陷入两个陷阱:
-
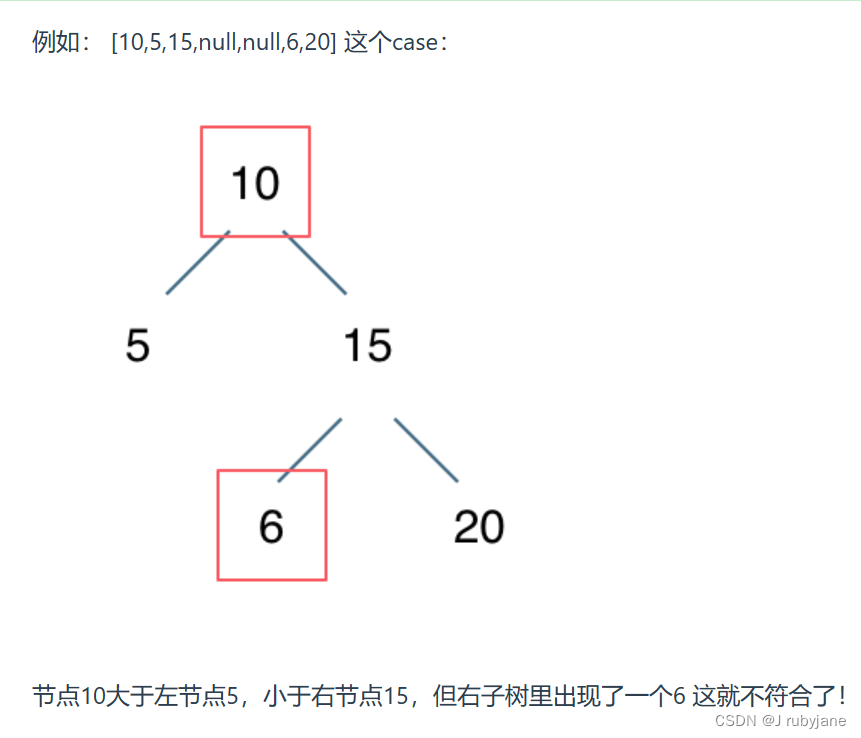
陷阱1:不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了。
if (root.val > root.left.val && root.val < root.right.val) {return true; } else {return false; }我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。所以以上代码的判断逻辑是错误的。
-
陷阱2


如②中方法所示。
①暴力解法 有效的二叉搜索树的中序遍历数组为升序数组(递归+for循环)
(1)递归,中序遍历,存放所有节点的val;判断中序遍历数组是否是升序数组。
(2)注:二叉搜索树中不能有重复元素。故数组前后元素不能=,要严格<才是升序。
import java.util.ArrayList;
class Solution {List<Integer> nodes = new ArrayList<>();public boolean isValidBST(TreeNode root) {// 递归,中序遍历,存放所有节点的valinorder(root);// 判断数组是否保持升序,至少有一个节点,如果只有一个节点,则不进入for循环for (int i = 0; i < nodes.size() - 1; i++) {if (nodes.get(i) >= nodes.get(i + 1)) return false;// 注意:不能等于,要严格小于才是升序}return true;}// 递归,中序遍历,存放所有节点的valpublic void inorder(TreeNode root) {if (root == null) return;//boolean result=false;isValidBST(root.left);//左nodes.add(root.val);isValidBST(root.right);//右}
}
②递归法 中序遍历二叉树过程中检测是否升序
class Solution {TreeNode max;public boolean isValidBST(TreeNode root) {if (root == null) return true;// 左boolean left = isValidBST(root.left);if (!left) return false;// 中if (max != null && max.val >= root.val) return false;max = root;// 右boolean right = isValidBST(root.right);return right;}
}
③迭代法(中序遍历)
统一迭代
class Solution {public boolean isValidBST(TreeNode root) {Stack<TreeNode> stack = new Stack<>();if (root == null) return true;stack.push(root);TreeNode max = null;while (!stack.isEmpty()) {TreeNode node = stack.peek();if (node != null) {stack.pop();if (node.right != null) {stack.push(node.right);//右}stack.push(node);//中stack.push(null);if (node.left != null) {stack.push(node.left);//左}} else {//中节点处理逻辑stack.pop();TreeNode preNode = stack.pop();if (max != null && max.val >= preNode.val) return false;max = preNode;}}return true;}
}
普通迭代(借助指针访问节点,栈处理元素)
class Solution {public boolean isValidBST(TreeNode root) {Stack<TreeNode> st = new Stack<>();if (root == null) return true;TreeNode cur = root;TreeNode max = null;while (cur != null || !st.isEmpty()) {if (cur != null) {st.push(cur);cur = cur.left;//左} else {TreeNode node = st.pop();if (max != null && max.val >= node.val) return false;//中max = node;cur = node.right;//右}}return true;}
}
相关文章:

代码随想录算法训练营第二十天| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
系列文章目录 目录 系列文章目录654.最大二叉树递归法[左闭右开)[左闭右闭] 617.合并二叉树递归法(前中后序都可,以前序为例)迭代法(类似 101. 对称二叉树 写法,可用双端队列/单端队列<栈>,以单端队列…...

2014年认证杯SPSSPRO杯数学建模A题(第二阶段)轮胎的花纹全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 A题 轮胎的花纹 原题再现: 轮胎被广泛使用在多种陆地交通工具上。根据性能的需要,轮胎表面常会加工出不同形状的花纹。在设计轮胎时,往往要针对其使用环境,设计出相应的花纹形状。 第二阶段问…...
C#全新一代医院手术麻醉系统围术期全流程源码
目录 一、麻醉学科的起源 二、麻醉前访视与评估记录单 患者基本信息 临床诊断 患者重要器官功能及疾病情况 病人体格情况分级 手术麻醉风险评估 拟施麻醉方法及辅助措施 其他需要说明的情况 访视麻醉医师签名 访视时间 与麻醉相关的检查结果 三、手术麻醉信息系统…...

Python 神器:一键下载 M3U8 并转换为 MP4
在这个数字时代,我们经常在网页上遇到各种精彩的视频,但往往只能观看而无法下载。今天,我将向大家介绍如何使用 Python 自动下载网页中的 M3U8 链接,并将其转换为 MP4 格式,让你轻松保存喜欢的视频! 一、准…...
vue3全局控制Element plus所有组件的文字大小
项目框架vue-右上角有控制全文的文字大小 实现: 只能控制element组件的文字及输入框等大小变化,如果是自行添加div,text, span之类的控制不了。 配置流程 APP.vue 使用element的provide,包含app <el-config-provider :locale"loca…...
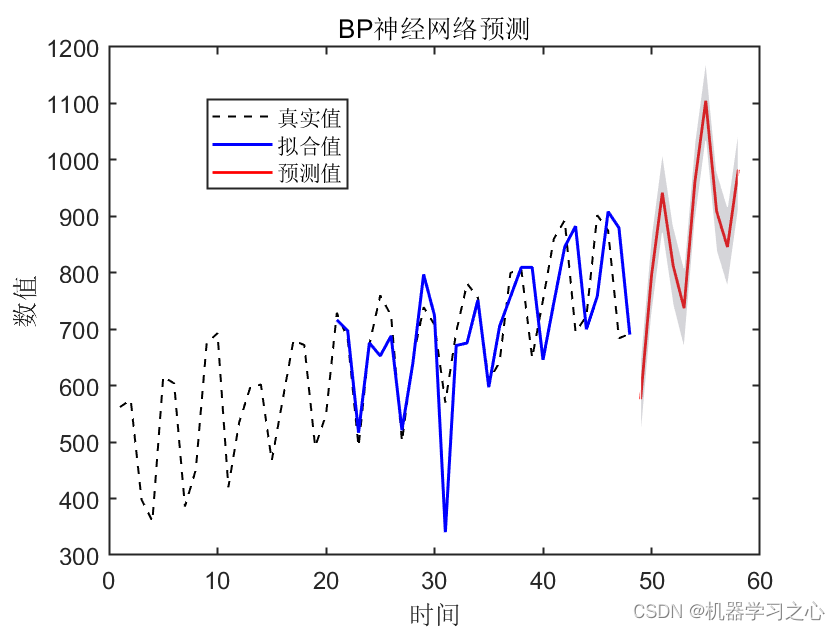
区间预测 | Matlab实现带有置信区间的BP神经网络时间序列未来趋势预测
区间预测 | Matlab实现带有置信区间的BP神经网络时间序列未来趋势预测 目录 区间预测 | Matlab实现带有置信区间的BP神经网络时间序列未来趋势预测预测效果基本介绍研究回顾程序设计参考资料预测效果 基本介绍 BP神经网络(Backpropagation neural network)是一种常用的人工神…...

Matlab中的脚本和函数
Matlab中的脚本和函数 文章目录 Matlab中的脚本和函数脚本创建脚本代码注释函数创建函数局部函数嵌套函数私有函数匿名函数补充知识函数句柄测试环境:Win11 + Matlab R2021a 脚本 Matlab脚本是最简单的程序文件类型。它们可用于自动执行一系列 Matlab 命令,如命令行重复执…...

使用 nohup java - jar 不输出nohup日志
使用 nohup 命令来运行 Java 程序,并且不让输出写入 nohup.out 文件,可以使用重定向操作符 > 将标准输出重定向到 /dev/null 文件中。这样可以将输出丢弃,而不会写入日志文件。下面是具体的命令: nohup java -jar your_progra…...
Linux系统中安装一些常用的插件备用
Linux系统中安装一些常用的插件备用 1.安装wget yum -y install wget 2.安装vim yum -y install vim-enhanced 3.更换yum源为国内的阿里云源(选择) 1、备份CentOS-Base.repo mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.…...
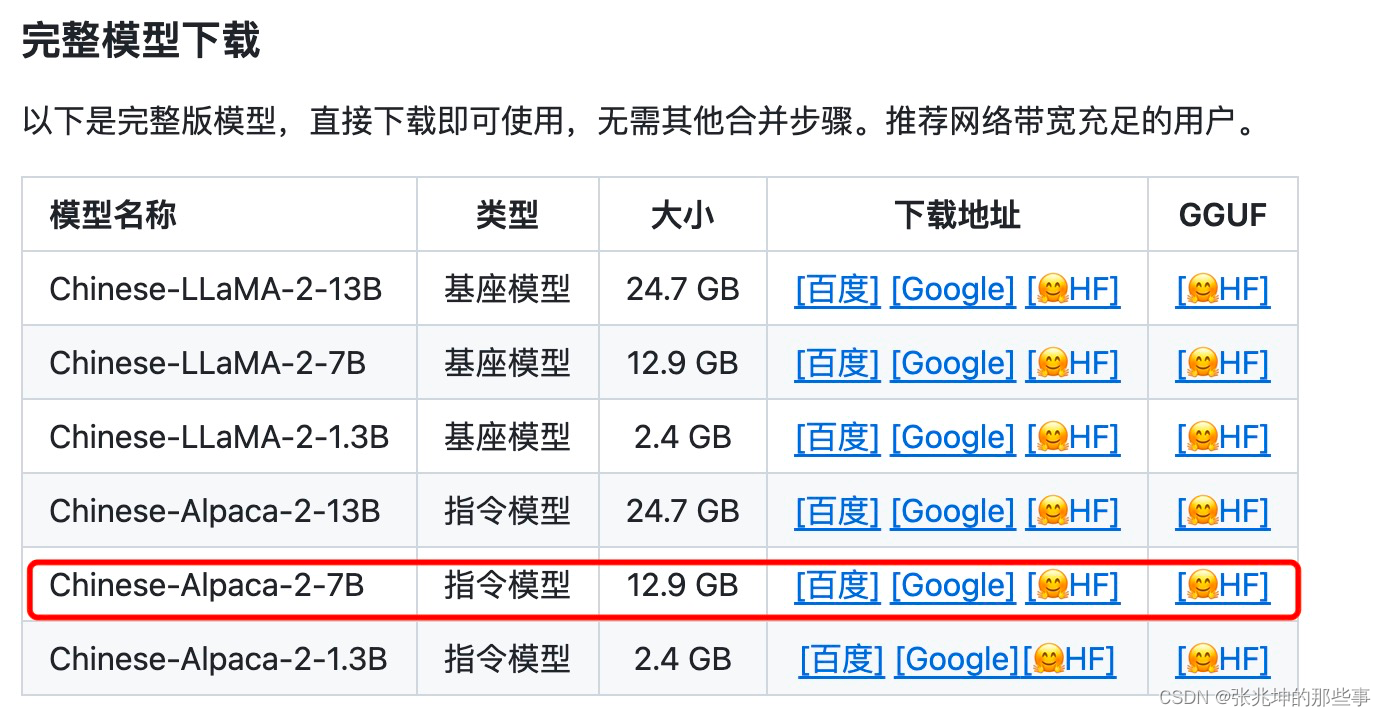
笔记本电脑上部署LLaMA-2中文模型
尝试在macbook上部署LLaMA-2的中文模型的详细过程。 (1)环境准备 MacBook Pro(M2 Max/32G); VMware Fusion Player 版本 13.5.1 (23298085); Ubuntu 22.04.2 LTS; 给linux虚拟机分配8*core CPU 16G RAM。 我这里用的是16bit的量化模型,…...
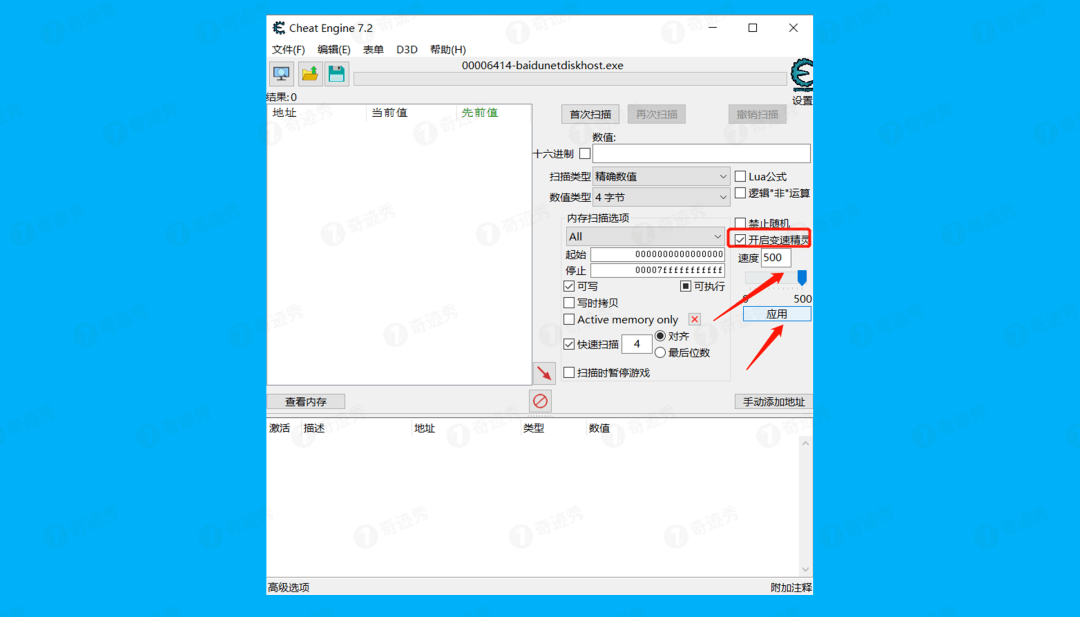
百度云加速方法「Cheat Engine」
加速网盘下载 相信经常玩游戏的小伙伴都知道「Cheat Engine」这款游戏内存修改器,它除了能对游戏进行内存扫描、调试、反汇编 之外,还能像变速齿轮那样进行本地加速。 这款专注游戏的修改器,被大神发现竟然还能加速百度网盘资源下载…...
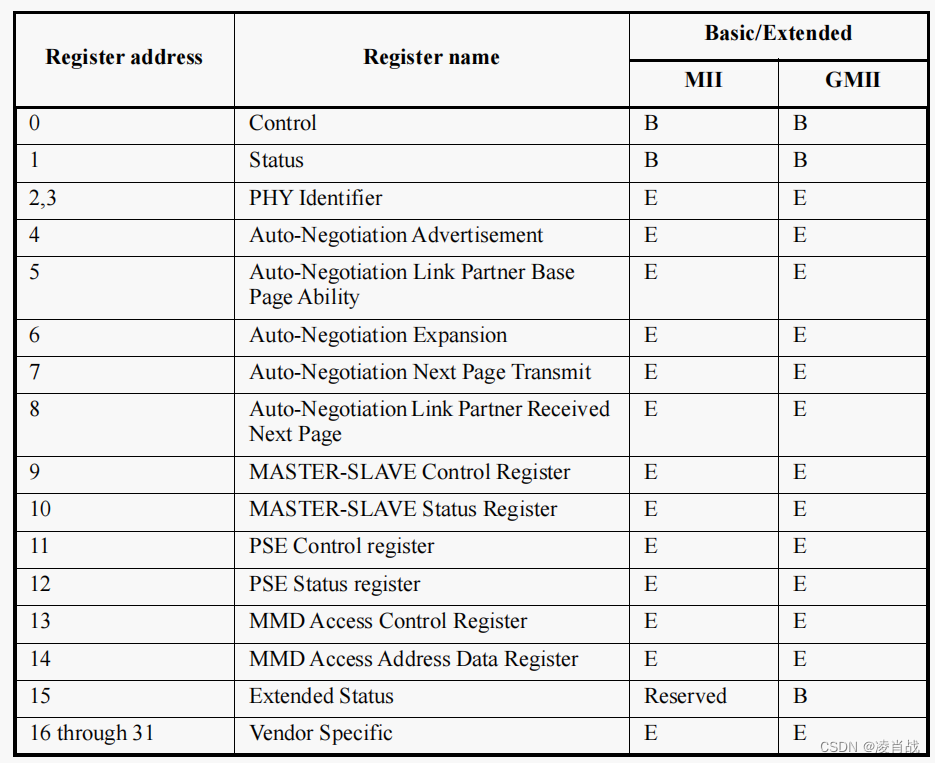
SOC内部集成网络MAC外设+ PHY网络芯片方案:PHY芯片基础知识
一. 简介 本文简单了解一下 "SOC内部集成网络MAC外设 PHY网络芯片方案" 这个网络硬件方案中涉及的 PHY网络芯片的基础知识。 二. PHY芯片基础知识 PHY 是 IEEE 802.3 规定的一个标准模块。 1. IEEE规定了PHY芯片的前 16个寄存器功能是一样的 前面说了…...

openGauss 6.0.0-RC1 版本正式发布!
openGauss 6.0.0-RC1版本正式上线! openGauss 6.0.0-RC1是社区最新发布的创新版本,版本生命周期为0.5年。(创新版本命名:由原方案 XX.1.0 Preview (例:5.1.0 preview),调整为现方案 XX.0.0-RCx&…...
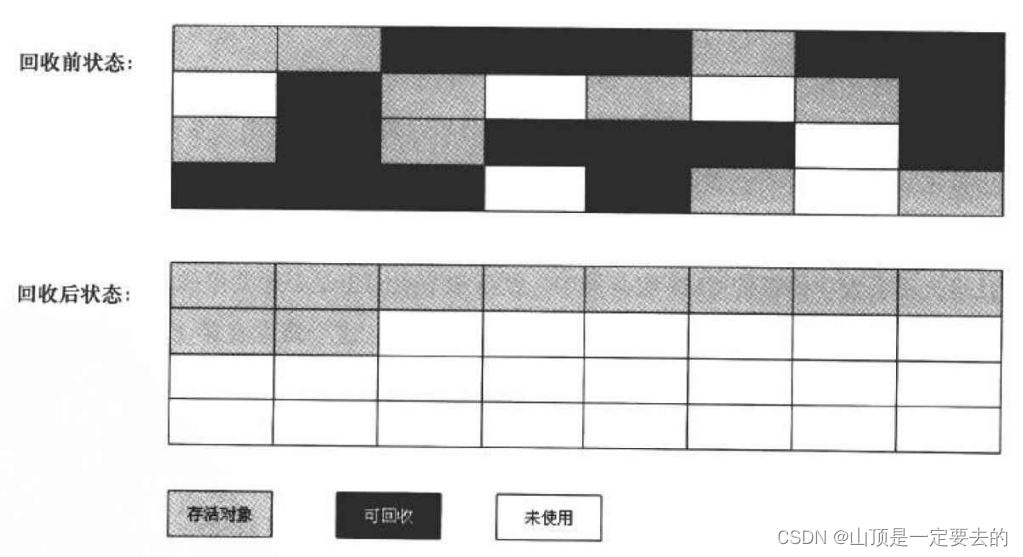
【JVM】关于JVM垃圾回收
文章目录 🌴死亡对象的判断算法🌸引用计数算法🌸可达性分析算法 🌳垃圾回收算法🌸标记-清除算法🌸复制算法🌸标记-整理算法🌸分代算法🌸哪些对象会进入新生代?…...

Unity照片墙简易圆形交互效果总结
还要很多可以优化的点地方,有兴趣的可以做 比如对象的销毁和生成可以做成对象池,走到最左边后再移动到最右边循环利用 分析过程文件,采用Blender,资源已上传,可以播放动画看效果,下面截个图: …...

Unity2018发布安卓报错 Exception: Gradle install not valid
Unity2018发布安卓报错 Exception: Gradle install not valid Exception: Gradle install not valid UnityEditor.Android.GradleWrapper.Run (System.String workingdir, System.String task, System.Action1[T] progress) (at <c67d1645d7ce4b76823a39080b82c1d1>:0) …...

蓝桥杯省赛刷题——题目 2656:刷题统计
刷题统计OJ链接:蓝桥杯2022年第十三届省赛真题-刷题统计 - C语言网 (dotcpp.com) 题目描述 小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。请你帮小明计算,按照计划他将在第几…...

Python爬虫之异步爬虫
异步爬虫 一、协程的基本原理 1、案例 案例网站:https://www.httpbin.org/delay/5、这个服务器强制等待了5秒时间才返回响应 测试:用requests写一个遍历程序,遍历100次案例网站: import requests import logging import time…...
【Web】NSSCTF Round#20 Basic 个人wp
目录 前言 真亦假,假亦真 CSDN_To_PDF V1.2 前言 感谢17👴没让我爆零 真亦假,假亦真 直接getshell不行,那就一波信息搜集呗,先开dirsearch扫一下 扫的过程中先试试常规的robots.txt,www.zip,shell.phps,.git,.sv…...

【Java笔记】实现延时队列1:JDK DelayQueue
文章目录 需求创建订单类创建延时队列优缺点 Reference JDK DelayQueue是一个无阻塞队列,底层是 PriorityQueue 需求 经典的订单超时取消 创建订单类 放入DelayQueue的对象需要实现Delayed接口 public interface Delayed extends Comparable<Delayed> {…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
