蓝桥杯省赛刷题——题目 2656:刷题统计

刷题统计OJ链接:蓝桥杯2022年第十三届省赛真题-刷题统计 - C语言网 (dotcpp.com)
题目描述
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于 n 题?
输入格式
输入一行包含三个整数 a, b 和 n.
输出格式
输出一个整数代表天数。
样例输入
10 20 99
样例输出
8
提示
对于 50% 的评测用例,1 ≤ a, b, n ≤ 10^6 . 对于 100% 的评测用例,1 ≤ a, b, n ≤ 10^18 .
C++:
#include <iostream>
using namespace std;
int main()
{long long int a, b, n, sum, k, t;//题目要求n的范围<=10^18所以我们这边要用long longcin >> a >> b >> n;sum = a * 5 + b * 2;//一周能刷的题目数量k = n / sum;//能刷几周t = n - sum * k;//刷的最大周后剩余的题if (t == 0){cout << 7 * k << endl;}else if(t<=a*5)//五天内能刷完{if (t % a == 0){cout << 7 * k + t / a << endl;}else{cout << 7 * k + t / a + 1;}}else if(t>a*5)//五天内刷不完{if ((t - a * 5) > b)//六天内刷不完{cout << 7 * k + 7 << endl;}else{cout << 7 * k + 6 << endl;}}return 0;
}运行结果:


PS:看到这里了,码字不易,给个一键三连鼓励一下吧!有不足或者错误之处欢迎在评论区指出!
相关文章:

蓝桥杯省赛刷题——题目 2656:刷题统计
刷题统计OJ链接:蓝桥杯2022年第十三届省赛真题-刷题统计 - C语言网 (dotcpp.com) 题目描述 小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。请你帮小明计算,按照计划他将在第几…...

Python爬虫之异步爬虫
异步爬虫 一、协程的基本原理 1、案例 案例网站:https://www.httpbin.org/delay/5、这个服务器强制等待了5秒时间才返回响应 测试:用requests写一个遍历程序,遍历100次案例网站: import requests import logging import time…...
【Web】NSSCTF Round#20 Basic 个人wp
目录 前言 真亦假,假亦真 CSDN_To_PDF V1.2 前言 感谢17👴没让我爆零 真亦假,假亦真 直接getshell不行,那就一波信息搜集呗,先开dirsearch扫一下 扫的过程中先试试常规的robots.txt,www.zip,shell.phps,.git,.sv…...

【Java笔记】实现延时队列1:JDK DelayQueue
文章目录 需求创建订单类创建延时队列优缺点 Reference JDK DelayQueue是一个无阻塞队列,底层是 PriorityQueue 需求 经典的订单超时取消 创建订单类 放入DelayQueue的对象需要实现Delayed接口 public interface Delayed extends Comparable<Delayed> {…...

npm淘宝镜像源切换
查询 npm config get registry注意因为淘宝的镜像域名更换,https://registry.npm.taobao.org域名HTTPS证书到期更换为https://registry.npmmirror.com/ 切换 npm config set registry https://registry.npmmirror.com/...
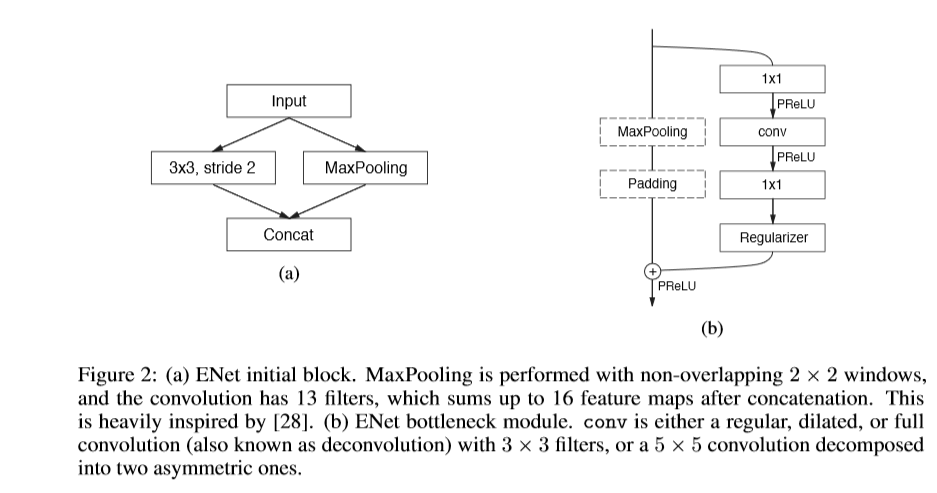
ENet——实时语义分割的深度神经网络架构与代码实现
概述 在移动设备上执行实时像素级分割任务具有重要意义。现有的基于分割的深度神经网络需要大量的浮点运算,并且通常需要较长时间才能投入使用。本文提出的ENet架构旨在减少潜在的计算负担。ENet在保持或提高分割精度的同时,相比现有的分割网络…...
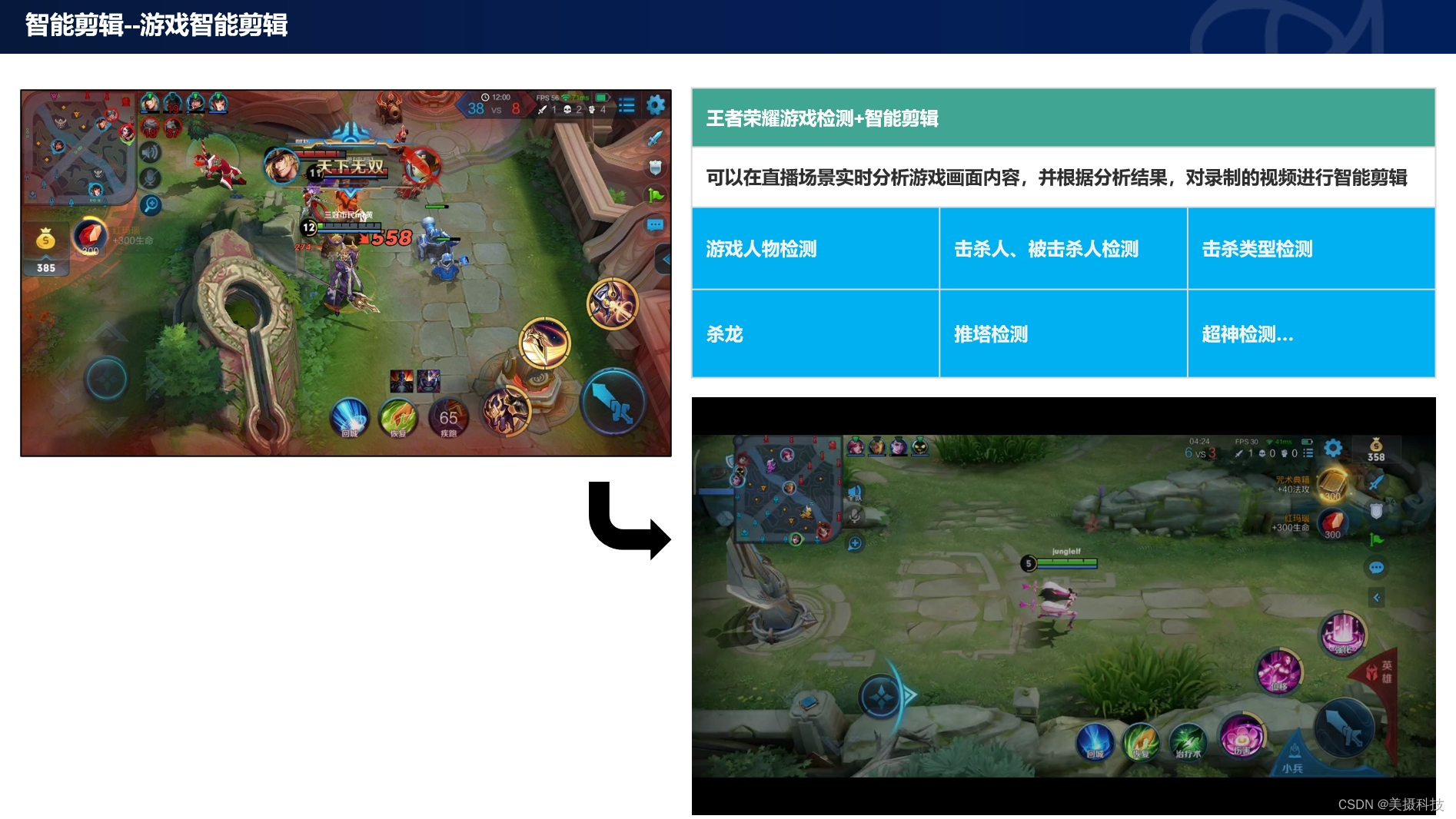
游戏领域AI智能视频剪辑解决方案
游戏行业作为文化创意产业的重要组成部分,其发展和创新速度令人瞩目。然而,随着游戏内容的日益丰富和直播文化的兴起,传统的视频剪辑方式已难以满足玩家和观众日益增长的需求。美摄科技,凭借其在AI智能视频剪辑领域的深厚积累和创…...

腾讯云轻量2核2G3M云服务器优惠价格61元一年,限制200GB月流量
腾讯云轻量2核2G3M云服务器优惠价格61元一年,配置为轻量2核2G、3M带宽、200GB月流量、40GB SSD盘,腾讯云优惠活动 yunfuwuqiba.com/go/txy 活动链接打开如下图: 腾讯云轻量2核2G云服务器优惠价格 腾讯云:轻量应用服务器100%CPU性能…...
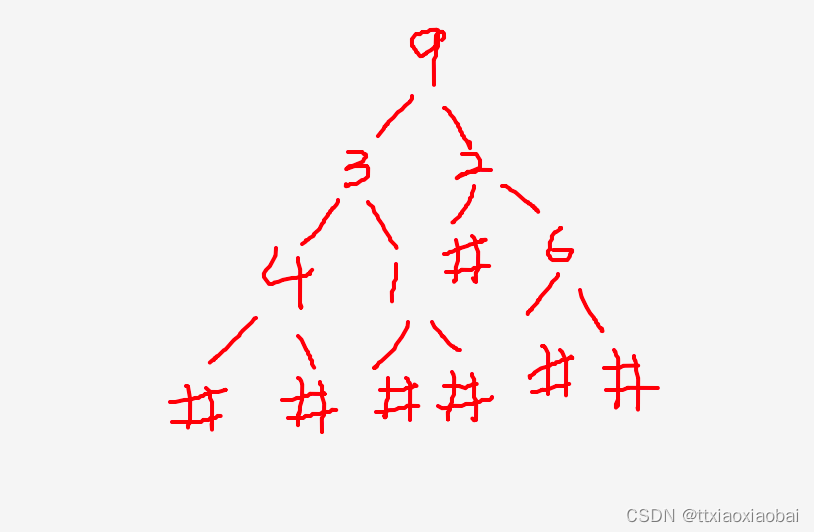
leecode 331 |验证二叉树的前序序列化 | gdb 调试找bug
计算的本质是数据的计算 数据的计算需要采用格式化的存储, 规则的数据结果,可以快速的按照指定要求存储数据 这里就不得不说二叉树了,二叉树应用场景真的很多 本题讲的是,验证二叉树的前序序列化 换言之,不采用建立树的…...

服务器安全事件应急响应排查方法
针对服务器操作系统的安全事件也非常多的。攻击方式主要是弱口令攻击、远程溢出攻击及其他应用漏洞攻击等。分析安全事件,找到入侵源,修复漏洞,总结经验,避免再次出现安全事件,以下是参考网络上文章,总结的…...

数码视讯Q7盒子刷armbian或emuelec的一些坑
首先,我手头的盒子是nand存储的,如果是emmc的,会省事很多…… 以下很多结论是我的推测,不一定准确。 1,原装安卓系统不支持SD卡或U盘启动,所以只能进uboot修改启动参数 2,原装安卓系统应该是…...

2_2.Linux中的远程登录服务
# 一.Openssh的功能 # 1.sshd服务的用途# #作用:可以实现通过网络在远程主机中开启安全shell的操作 Secure SHell >ssh ##客户端 Secure SHell daemon >sshd ##服务端 2.安装包# openssh-server 3.主配置文件# /etc/ssh/sshd_conf 4.…...
Spring Boot集成JPA快速入门demo
1.JPA介绍 JPA (Java Persistence API) 是 Sun 官方提出的 Java 持久化规范。它为 Java 开发人员提供了一种对象/关联映射工具来管理 Java 应用中的关系数据。他的出现主要是为了简化现有的持久化开发工作和整合 ORM 技术,结束现在 Hibernate,TopLink&am…...
深度学习理解及学习推荐(持续更新)
主推YouTuBe和Bilibili 深度学习博主推荐: Umar Jamil - YouTubehttps://www.youtube.com/umarjamilai StatQuest with Josh Starmer - YouTubehttps://www.youtube.com/statquest RNN Illustrated Guide to Recurrent Neural Networks: Understanding the Int…...

【C语言】贪吃蛇【附源码】
欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 一、游戏说明: 一个基于C语言链表开发的贪吃蛇游戏: 1. 按方向键上下左右,可以实现蛇移动方向的改变。 2. 短时间长按方向键上下左右其中之一,可实现蛇向该方向的短时间…...
【技巧】压缩文件如何设置“自动加密”?
很多人会在压缩文件的时候,同时设置密码,以此保护私密文件。如果经常需要压缩文件并设置密码,不妨使用解压缩软件的“自动加密”功能,更省时省力。 下面介绍WinRAR解压缩软件的两种“自动加密”的方法,一起来看看吧&a…...

内网穿透时报错【Bad Request This combination of host and port requires TLS.】的原因
目录 前言:介绍一下内网穿透 1.内网直接https访问(可以正常访问) 程序配置的证书 2.内网穿透后,通过外网访问 3.原因 4.内网非https的Web应用,使用https后,也变成了https访问 5.题外话 感觉自己的web应用配置了…...
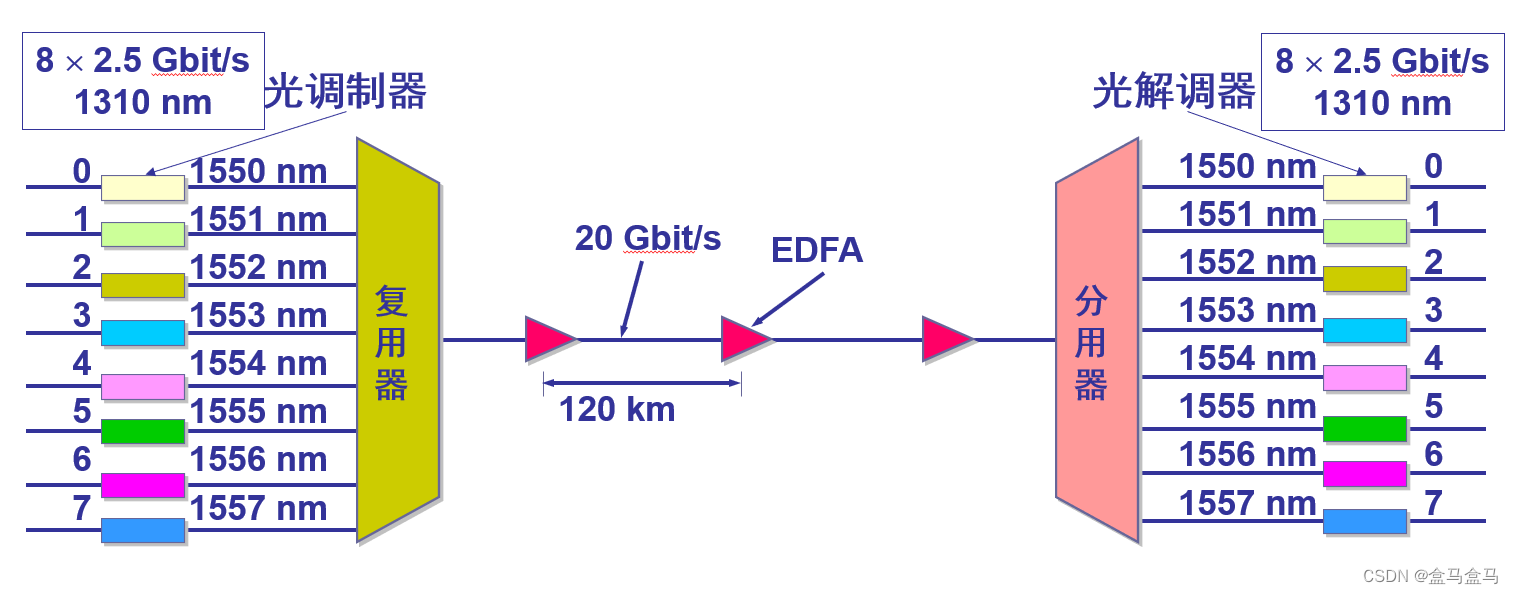
计算机网络:物理层 - 信道复用
计算机网络:物理层 - 信道复用 频分复用时分复用统计时分复用波分复用码分复用 计算机网络中,用户之间通过信道进行通信,但是信道是有限的,想要提高网络的效率,就需要提高信道的利用效率。因此计算机网络中普遍采用信道…...

【算法集训】基础算法:滑动窗口
定义一个快慢指针,用于截取数组中某一段信息。同时可以改变快慢指针的值来获取结果,这个过程比较像滑动。 1493. 删掉一个元素以后全为 1 的最长子数组 定义快慢指针快指针先走,如果到了第二个0上的时候。前面1的个数就是fast - slow - 1&a…...
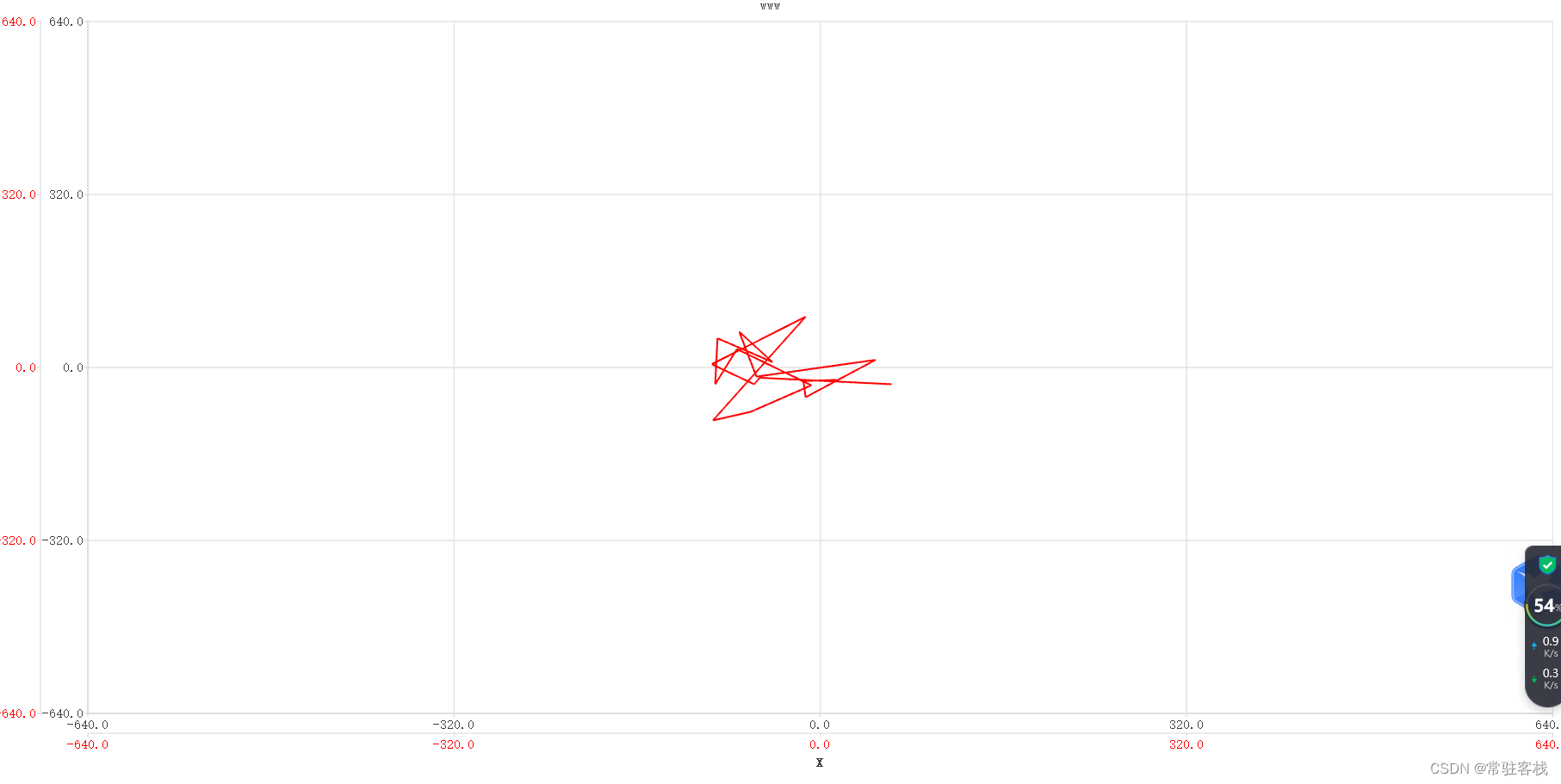
QT 二维坐标系显示坐标点及点与点的连线-通过定时器自动添加随机数据点
QT 二维坐标系显示坐标点及点与点的连线-通过定时器自动添加随机数据点 功能介绍头文件C文件运行过程 功能介绍 上面的代码实现了一个简单的 Qt 应用程序,其功能包括: 创建一个 MainWindow 类,继承自 QMainWindow,作为应用程序的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
