C语言数据结构易错知识点(6)(快速排序、归并排序、计数排序)
快速排序属于交换排序,交换排序还有冒泡排序,这个太简单了,这里就不再讲解。
归并排序和快速排序都是采用分治法实现的排序,理解它们对分支思想的感悟会更深。
计数排序属于非比较排序,在数据集中的情况下可以考虑使用。这时效率也比较高。
下面讲解一下这三种排序在代码实现上易错的地方:
一、快速排序
快速排序通过每趟排序确定一个数的最终位置最终实现将数组变得有序的功能。主要有三种方法,第一种方法偏向常规,第二种方法是双指针法,第三种方法是非递归法,除此之外,还有一些优化的方案,如挖坑法,随机确定key,三数取中,后面代码实现上会简要说明。
方法一:常规法
1.代码实现:
void QuickSort1(int* arr, int left, int right)
{int start = left, end = right, key = left;if (left >= right)return;while (left < right){while (left < right && arr[right] >= arr[key])right--;while (left < right && arr[left] <= arr[key])left++;swap(&arr[left], &arr[right]);}swap(&arr[key], &arr[left]);key = left;QuickSort1(arr, start, key - 1);QuickSort1(arr, key + 1, end);
}
2.下面是单趟排序的逻辑:

至于需要注意的点,就是当key在左侧时,一定要右侧先动,左侧再动,这样才能保证相遇点的值小于等于arr[key](这个结论可以画图证明,这里就不展开了),当然,逆序同理。
3.下面是整体逻辑的详细解读,写代码时一定要注意细节,后续快排代码不再重复:

4.由于相遇点的值小于等于arr[key]这个结论一定程度上难以理解,于是就出现了一种优化方案——挖坑法,代码如下:
void QuickSort5(int* arr, int left, int right)
{if (left >= right)return;int start = left, end = right, key = left, piti = left;//存储坑的下标int tmp = arr[key];//用来初始坑里的值while (left < right){while (left < right && arr[right] >= tmp)right--;if (left < right){arr[piti] = arr[right];piti = right;}while (left < right && arr[left] <= tmp)left++;if (left < right){arr[piti] = arr[left];piti = left;}}arr[piti] = tmp;key = piti;QuickSort5(arr, start, key - 1);QuickSort5(arr, key + 1, end);
}5.当数组接近有序时,每次调用后key的位置都会很偏,导致递归次数接近N,总时间复杂度来到O(N ^ 2),因此取key尤为关键,关键在于不要一来就取到最小值,因此随机取key和三数取中可以一定程度上缓解这个问题:,代码如下:
三数取中:
int GetMid(int* arr, int left, int right)
{int mid = (left + right) / 2;if (arr[mid] >= arr[left]){if (arr[mid] < arr[right])return mid;else{if (arr[left] < arr[right])return right;elsereturn left;}}else{if (arr[mid] > arr[right])return mid;else{if (arr[right] < arr[left])return left;elsereturn right;}}}
随机取key:
int key = rand() % (right - left + 1) + left;//随机值但是这些方法依旧不能完全消除快排的缺陷,当数组是1111111111这种时,时间复杂度依然会变成O(N ^ 2)
6.时间复杂度分析
快排的时间复杂度是O(NlogN),分析方法如下:
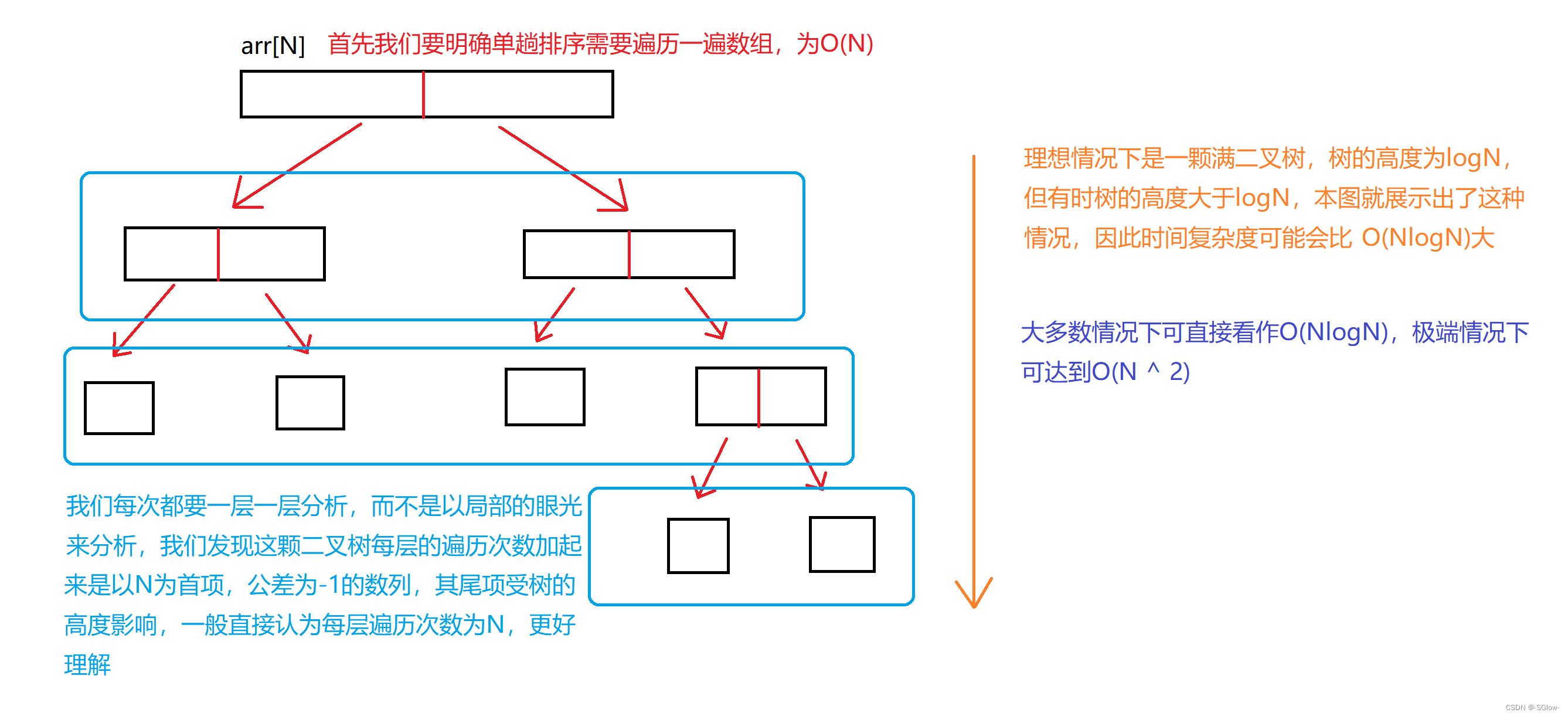
需要补充的是,logN与N的差别很大,N-logN依然是N的量级,举个例子:已知2的10次方是1024,假如有1024个数据,在快排中,单趟排序的遍历次数为1024、1023、1022一直到1014(末项可能会更小,但不会小多少),我们发现,这些数字差别很小,几乎是由N来决定的,所以上面图中说我们一般可以将单趟遍历的次数看作N
方法二:双指针法
这个方法的代码实现比较简单,关键在于prev指针和cur指针之间嵌入大于arr[key]的值,注意每次arr[prev]的下一个元素都是大于arr[key]的(当然也有可能相同或者没有元素,但是在这两种特殊情况下对我们功能的实现没有影响),最后交换arr[key]和arr[prev]达到一样的效果,使右侧大于arr[key],左侧小于等于arr[key]。后续逻辑相同。
代码实现如下:
void QuickSort3(int* arr, int left, int right)
{int prev = left, cur = left + 1, key = left;if (left > right)return;while (cur <= right){if (arr[cur] > arr[key])cur++;elseswap(&arr[++prev], &arr[cur++]);}swap(&arr[key], &arr[prev]);key = prev;QuickSort3(arr, left, key - 1);QuickSort3(arr, key + 1, right);
}
方法三:非递归法
这种方法利用了前序遍历和栈的相似性。为什么说是前序遍历呢?因为在遍历时,该层遍历还同时保存了左递归和右递归的必要信息,就像二叉树的父节点能够找到子节点,而子节点找不到父节点。如果是中序或后序就没有这样的特性,就不适合用栈或队列等数据结构来实现。这也是为什么归并排序不适合用栈和队列来实现非递归。
代码如下:
void QuickSort4(int* arr, int left, int right)
{Stack s;StackInit(&s);StackPush(&s, right), StackPush(&s, left);//从右向左入栈while (!isStackEmpty(&s)){int left = StackTop(&s);StackPop(&s);int right = StackTop(&s);StackPop(&s);int prev = left, cur = left + 1, key = left;//从左向右取数据while (cur <= right){if (arr[cur] > arr[key])cur++;elseswap(&arr[++prev], &arr[cur++]);}swap(&arr[key], &arr[prev]);key = prev;if(key + 1 < right)StackPush(&s, right), StackPush(&s, key + 1);//后取得if(left < key - 1)StackPush(&s, key - 1), StackPush(&s, left);//先取得}StackDestroy(&s);
}
相关栈的功能实现如下:
void StackInit(Stack* ps)
{ps->arr = NULL;ps->capacity = ps->size = 0;
}void StackPush(Stack* ps, int val)
{if (ps->capacity == ps->size){ps->capacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;int* tmp = (int*)realloc(ps->arr, sizeof(int) * ps->capacity);assert(tmp);ps->arr = tmp;}ps->arr[ps->size++] = val;
}int StackTop(Stack* ps)
{return ps->arr[ps->size - 1];
}void StackPop(Stack* ps)
{ps->size--;
}bool isStackEmpty(Stack* ps)
{return ps->size == 0;
}void StackDestroy(Stack* ps)
{free(ps->arr), ps->arr = NULL;ps->capacity = ps->size = 0;}
需要注意入栈顺序是从右向左,右下标先入,左下标后入,右递归先入,左递归后入。基本逻辑和递归相似,理解了原理就很好写。
二、归并排序
归并排序一定程度上比较好理解,但非递归法需要注意的细节比较多
方法一:递归法
void _MergeSort(int* arr, int* tmp, int start, int end)
{if (start == end)return;int mid = (start + end) / 2;_MergeSort(arr, tmp, start, mid);_MergeSort(arr, tmp, mid + 1, end);int start1 = start, end1 = mid;int start2 = mid + 1, end2 = end;int i = start1;while (start1 <= end1 && start2 <= end2){if (arr[start1] <= arr[start2])tmp[i++] = arr[start1++];elsetmp[i++] = arr[start2++];}while (start1 <= end1){tmp[i++] = arr[start1++];}while (start2 <= end2){tmp[i++] = arr[start2++];}memmove(arr + start, tmp + start, sizeof(int) * (end - start + 1));
}void MergeSort1(int* arr, int size)
{int* tmp = (int*)malloc(sizeof(int) * size);assert(tmp);_MergeSort(arr, tmp, 0, size - 1);free(tmp), tmp = NULL;
}整体逻辑:
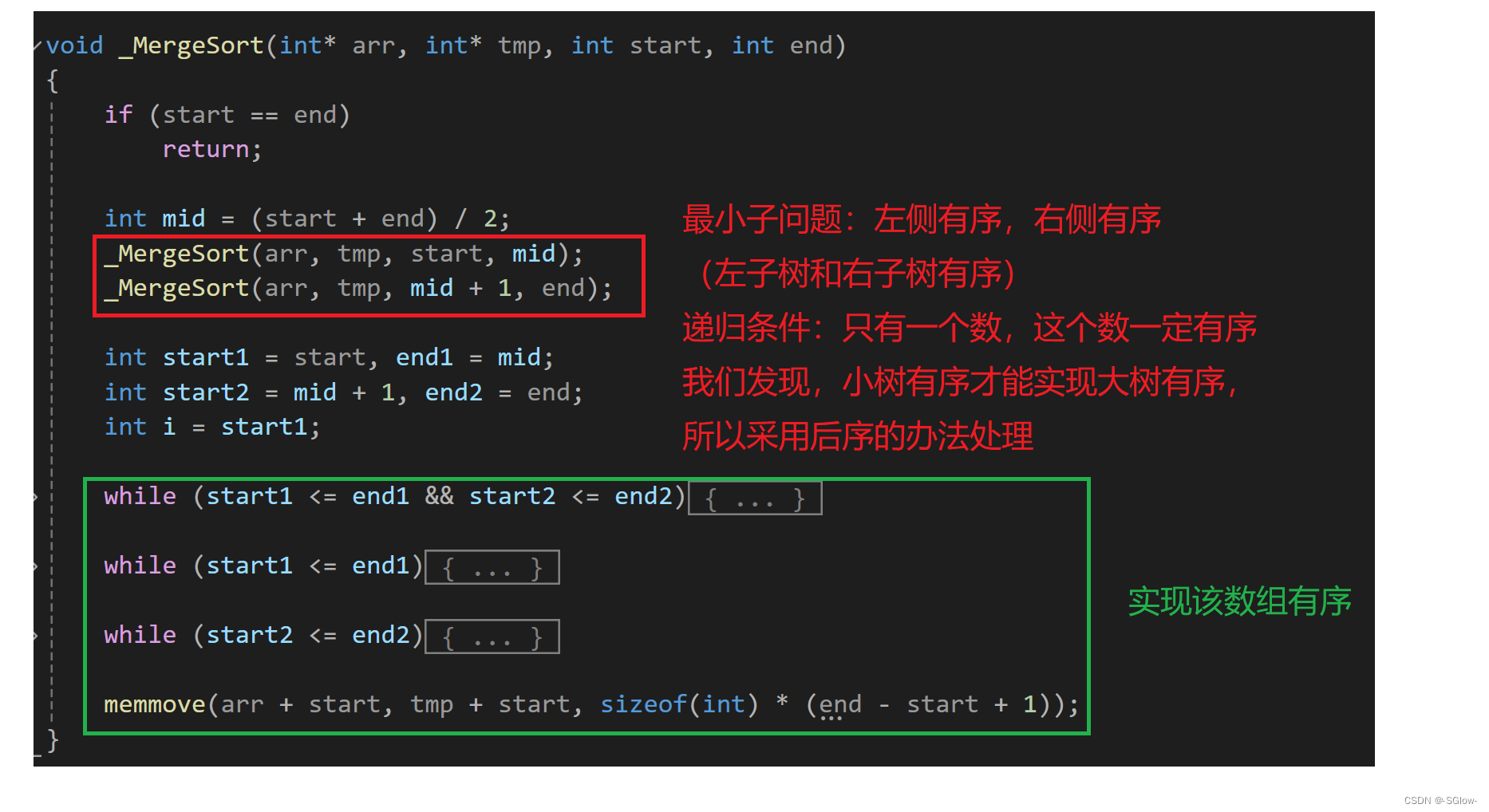
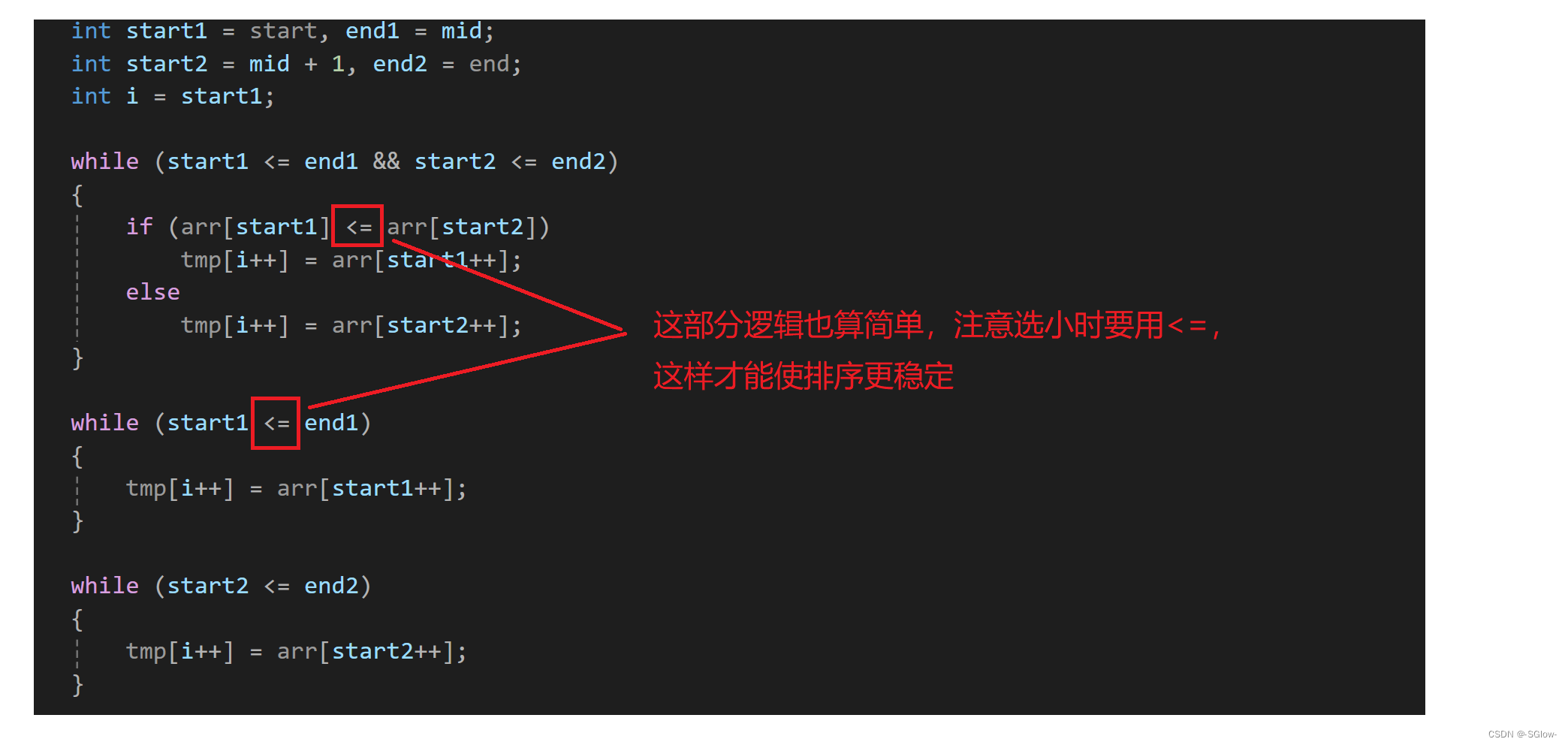
方法二:非递归法
非递归法理解起来较为困难,下面详细分析:
代码实现:
void MergeSort2(int* arr, int size)
{int* tmp = (int*)malloc(sizeof(int) * size);assert(tmp);int gap = 1;while (gap <= size){for (int i = 0; i < size; i += 2 * gap){int start1 = i, end1 = start1 + gap - 1;int start2 = end1 + 1, end2 = start2 + gap - 1;int j = start1;if (end1 >= size || start2 >= size)break;while (end2 >= size)end2--;while (start1 <= end1 && start2 <= end2){if (arr[start1] <= arr[start2])tmp[j++] = arr[start1++];elsetmp[j++] = arr[start2++];}while (start1 <= end1){tmp[j++] = arr[start1++];}while (start2 <= end2){tmp[j++] = arr[start2++];}memmove(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp), tmp = NULL;
}
1.整体逻辑
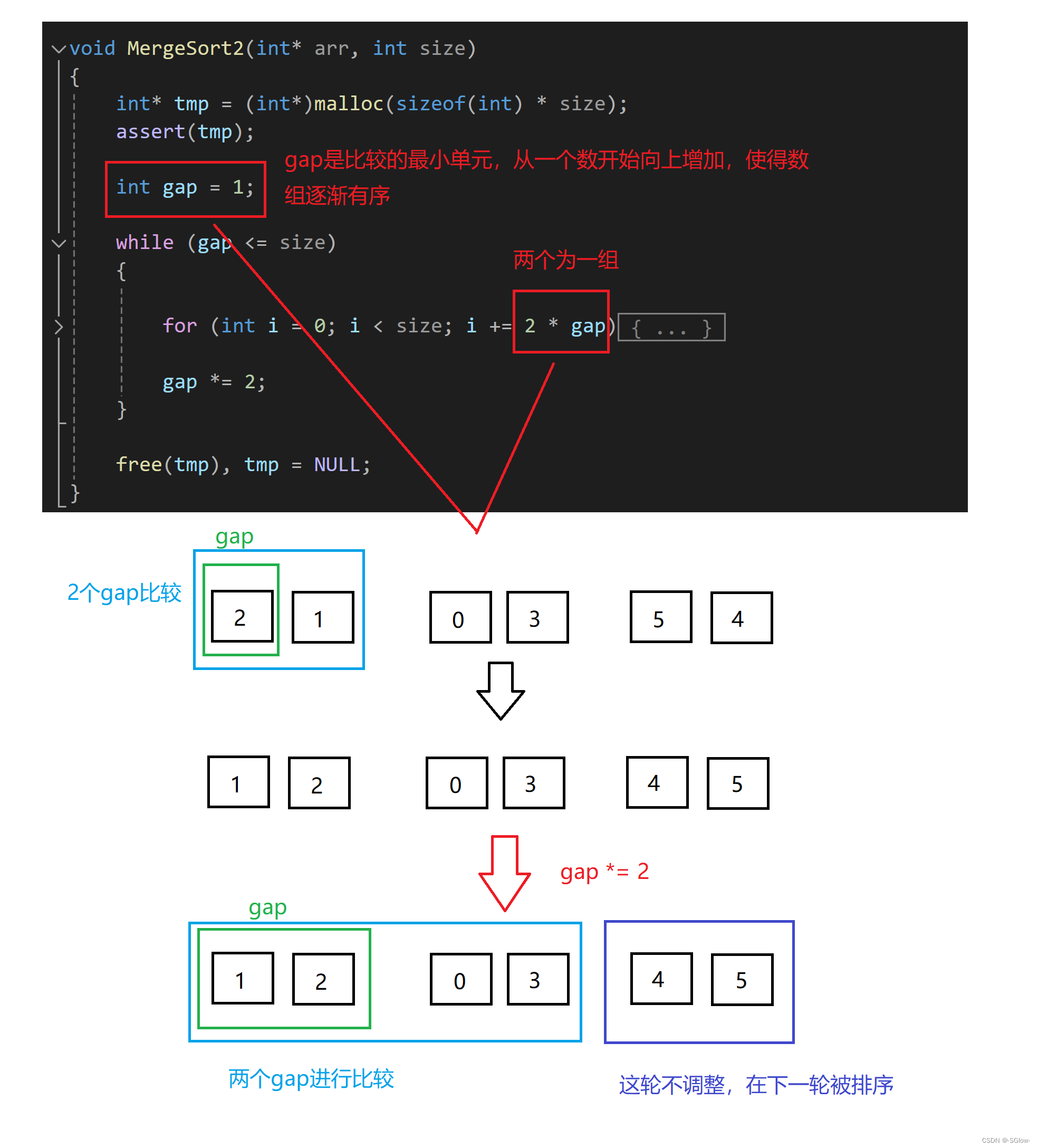
它的逻辑大体上和递归法相似,但非递归法是直接从最小元素开始向上归并。
2.非递归归并的难点在于数组前面归并是两两为一组,会导致有落单的情况,需要进行处理,上面这张图就展示出了一种情况,下面分析一下:

三、计数排序
这个排序非常简单,不做过多分析
代码实现:
void CountSort(int* arr, int size)
{int max = arr[0], min = arr[0];for (int i = 0; i < size; i++){if (arr[i] > max)max = arr[i];if (arr[i] < min)min = arr[i];}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));assert(count);for (int i = 0; i < size; i++){count[arr[i] - min]++;}for (int i = 0, j = 0; i < range; i++){while (count[i]--){arr[j++] = i + min;}}}注意这个方法用于数据集中时使用,这个时候效率很高。但分散数据就别用,会浪费大量空间。这个排序讨论其稳定性没有意义,因为它只能做到数值的排序,这些排序后没有意义。
相关文章:

C语言数据结构易错知识点(6)(快速排序、归并排序、计数排序)
快速排序属于交换排序,交换排序还有冒泡排序,这个太简单了,这里就不再讲解。 归并排序和快速排序都是采用分治法实现的排序,理解它们对分支思想的感悟会更深。 计数排序属于非比较排序,在数据集中的情况下可以考虑使…...

使用 React Router v6.22 进行导航
使用 React Router v6.22 进行导航 React Router v6.22 是 React 应用程序中最常用的路由库之一,提供了强大的导航功能。本文将介绍如何在 React 应用程序中使用 React Router v6.22 进行导航。 安装 React Router 首先,我们需要安装 React Router v6…...
单链表的插入和删除
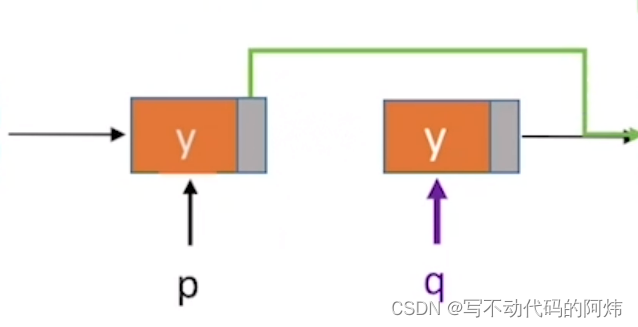
一、插入操作 按位序插入(带头结点): ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。 typedef struct LNode{ElemType data;struct LNode *next; }LNode,*LinkList;//在第i 个位置插插入元素e (带头结点) bool Li…...

全量知识系统 之“程序”详细设计 之 “絮”---开端“元素周期表”表示的一个“打地鼠”游戏
全量知识系统 之“程序”详细设计 概述-概要和纪要 序 絮(一个极简的开场白--“全量知识系统”自我介绍) 将整个“人生”的三个阶段 比作“幼稚园”三班 : 第一步【想】-- “感性”思维游戏:打地鼠 。学前教育-新生期&#x…...

【详细讲解WebView的使用与后退键处理】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

【Linux多线程】生产者消费者模型
【Linux多线程】生产者消费者模型 目录 【Linux多线程】生产者消费者模型生产者消费者模型为何要使用生产者消费者模型生产者消费者的三种关系生产者消费者模型优点基于BlockingQueue的生产者消费者模型C queue模拟阻塞队列的生产消费模型 伪唤醒情况(多生产多消费的…...
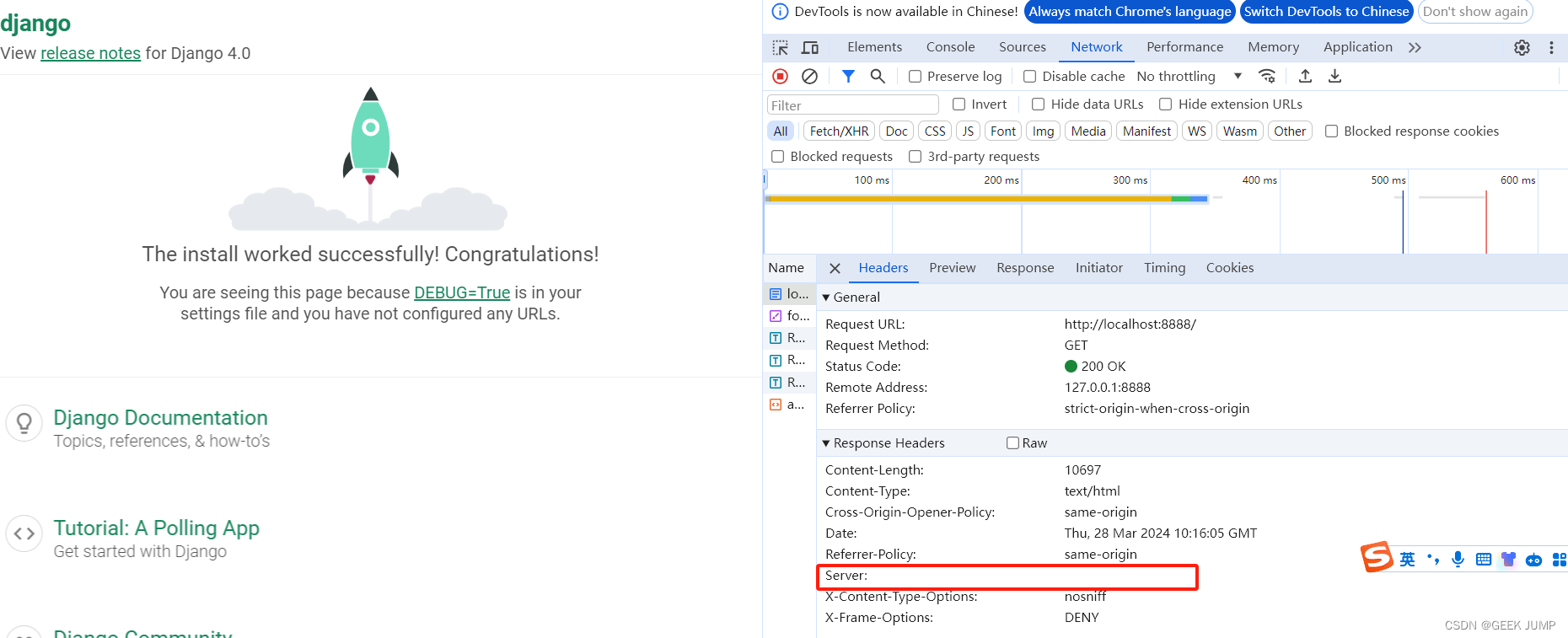
Django屏蔽Server响应头信息
一、背景 最近我们被安全部门的漏洞扫描工具扫出了一个服务端口的漏洞。这个服务本身是一个Django启动的web服务,并且除了登录页面,其它页面或者接口都需要进行登录授权才能进行访问。 漏洞扫描信息和提示修复信息如下: 自然这些漏洞如何修复,…...
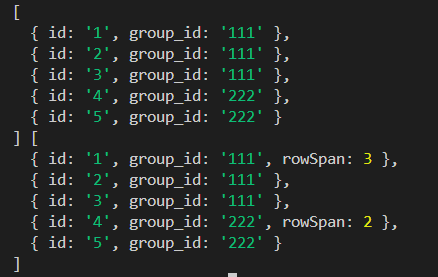
前端对数据进行分组和计数处理
js对数组数据的处理,添加属性,合并表格数据。 let data[{id:1,group_id:111},{id:2,group_id:111},{id:3,group_id:111},{id:4,group_id:222},{id:5,group_id:222} ]let tempDatadata; tempDatatempData.reduce((arr,item)>{let findarr.find(i>i…...

synchronized 和 lock
synchronized 和 Lock 都是 Java 中用于实现线程同步的机制,它们都可以保证线程安全。 # synchronized 介绍与使用 synchronized 可用来修饰普通方法、静态方法和代码块,当一个线程访问一个被 synchronized 修饰的方法或者代码块时,会自动获…...
ssh 公私钥(github)
一、生成ssh公私钥 生成自定义名称的SSH公钥和私钥对,需要使用ssh-keygen命令,这是大多数Linux和Unix系统自带的标准工具。下面,简单展示如何使用ssh-keygen命令来生成具有自定义名称的SSH密钥对。 步骤 1: 打开终端 首先,打开我…...

LangChain入门:8.打造自动生成广告文案的应用程序
在这篇技术博文中,我们将探讨如何利用LangChain框架的模板管理、变量提取和检查、模型切换以及输出解析等优势,打造一个自动生成广告文案的应用程序。 LangChain框架的优势 在介绍应用程序之前,让我们先了解一下LangChain框架的几个优势: 模板管理: 在大型项目中,文案可…...

AI如何影响装饰器模式与组合模式的选择与应用
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》《MYSQL应用》 💪🏻 制定明确可量化的目标,坚持默默的做事。 🚀 转载自热榜文章:设计模式深度解析:AI如何影响…...
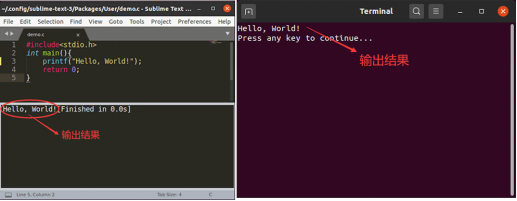
【C语言环境】Sublime中运行C语言时MinGW环境的安装
要知道,GCC 官网提供的 GCC 编译器是无法直接安装到 Windows 平台上的,如果我们想在 Windows 平台使用 GCC 编译器,可以安装 GCC 的移植版本。 目前适用于 Windows 平台、受欢迎的 GCC 移植版主要有 2 种,分别为 MinGW 和 Cygwin…...

Ubuntu18.04 下Ublox F9P 实现RTK (利用CORS服务无需自建基站)
本内容参考如下连接:Ubuntu下Ublox F9P利用CORS服务无需自建基站实现RTK-CSDN博客 一、Ublox F9P 硬件模块示意图 图中展示了Ublox F9P的接口,包括串口2(`UART1`和`UART2`),USB1。需要人为通过u-center(Ublox F9P的显示软件)软件设置以下功能: Ublox通过`UART1`向PC端发送…...
springboot+vue在idea上面的使用小结
1.在mac上面删除java的jdk方法: sudo rm -rfjdk的路径 sudo rm -rf /Users/like/Library/Java/JavaVirtualMachines/corretto-17.0.10/Contents/Home 2.查询 Mac的jdk版本和路径: /usr/libexec/java_home -V 3.mac上面查询和关闭idea的网页端口&…...

MyEclipse将项目的开发环境与服务器的JDK 版本保持一致
前言 我们使用MyEclipse开发Java项目开发中,偶尔会遇到因项目开发环境不协调,导致这样那样的问题,在这里以把所有环境调整为JDK1.6 为例。 操作步骤 1.Window-->Preferences-->Java-->Installed JRES 修改为 1.6版本 2.Window-->…...

为BUG编程:函数重载的烦恼 char *匹配bool而不是string
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 这是一个BUG。 运行环境为linu…...

C++第十四弹---模板初阶
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、泛型编程 2、函数模板 2.1、函数模板的概念 2.2、函数模板的格式 2.3、函数模板的原理 2.4、函数模板的实例化 2.5、模板参数的匹配原则 …...

C++--内联函数
当调用一个函数时,程序就会跳转到该函数,函数执行完毕后,程序又返回到原来调用该函数的位置的下一句。 函数的调用也需要花时间,C中对于功能简单、规模小、使用频繁的函数,可以将其设置为内联函数。 内联函数ÿ…...
java数组与集合框架(一) -- 数据结构,数组
数据结构 概述 为什么要讲数据结构? 任何一个有志于从事IT领域的人员来说,数据结构(Data Structure)是一门和计算机硬件与软件都密切相关的学科,它的研究重点是在计算机的程序设计领域中探讨如何在计算机中组织和存储…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
