【数据结构与算法初阶(c语言)】插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序、计数排序-全梳理(万字详解,干货满满,建议三连收藏)
目录
1.排序的概念及其运用
1.1排序的概念
1.2排序运用
1.3常见的排序算法
2.插入排序
2.1 原理演示:编辑
2.2 算法实现
2.3 算法的时间复杂度和空间复杂度分析
3.希尔排序
3.1算法思想
3.2原理演示
3.3代码实现
3.4希尔算法的时间复杂度
4.冒泡排序
4.1冒泡排序原理(图解)
4.2.冒泡排序实现
4.3冒泡排序封装为函数
4.4 冒泡排序代码效率改进。
5.堆排序
5.1升序建大堆,降序建小堆
5.2 建堆的时间复杂度
5.2.1 向下调整建堆
5.2.2向上调整建堆
5.3 排序实现
6.选择排序
6.1基本思想:
6.2算法演示
6.3代码实现
6.4时间复杂度分析
7.快速排序
7.1 hoare版本
7.1.1算法图解
7.1.2代码实现
7.1.3 算法优化---三数取中
7.2挖坑法快排
7.2.1算法图解
7.2.2 代码实现
7.3 前后指针法
7.4快速排序进一步优化
7.5快速排序非递归写法
8.归并排序
9.计数排序
10.结语
深度优先遍历 dfs : 先往深处走,走到没有了再往回,前序遍历 一般是递归
广度优先遍历 bfs 层序遍历 一般用队列
1.排序的概念及其运用
1.1排序的概念
1.2排序运用
1.3常见的排序算法

2.插入排序
算法思想:
和我们玩扑克牌整理牌的时候是非常相像的

将我们的摸到的牌作为手里的牌的最后一张,从倒数第一张开始到第一张逐次比较,如果当前牌大于前一张就放置在当前位置,如果小于那就向前移动,最坏的情况就是每次摸到牌都要逐渐比较放到最前面。
2.1 原理演示: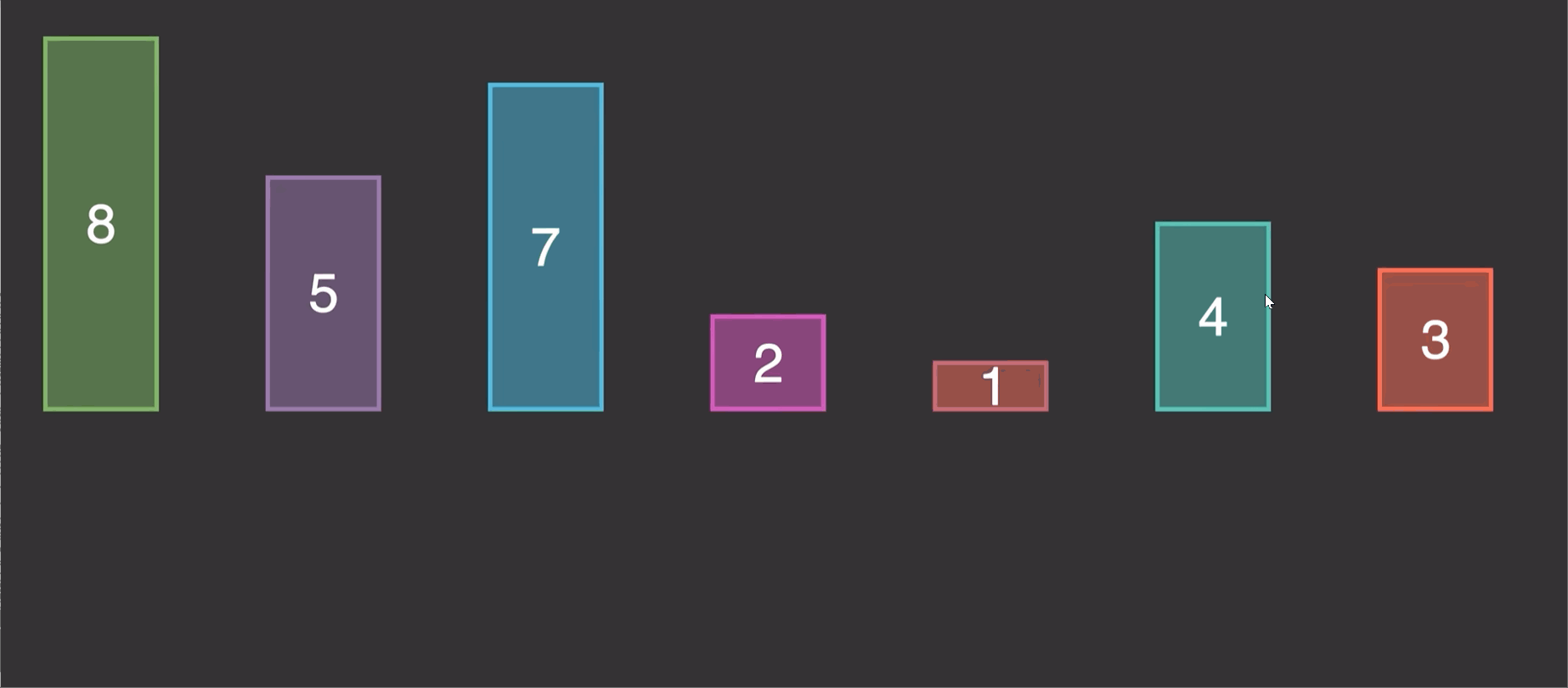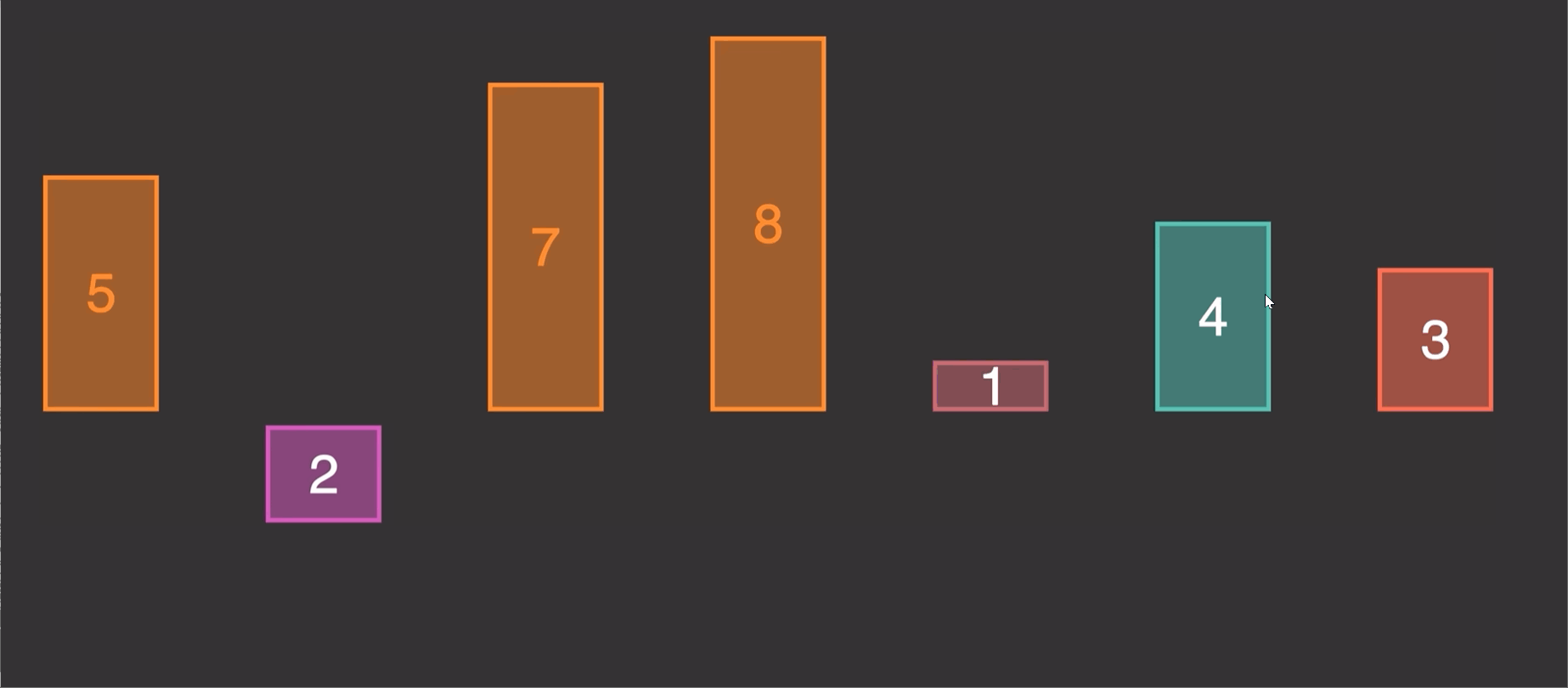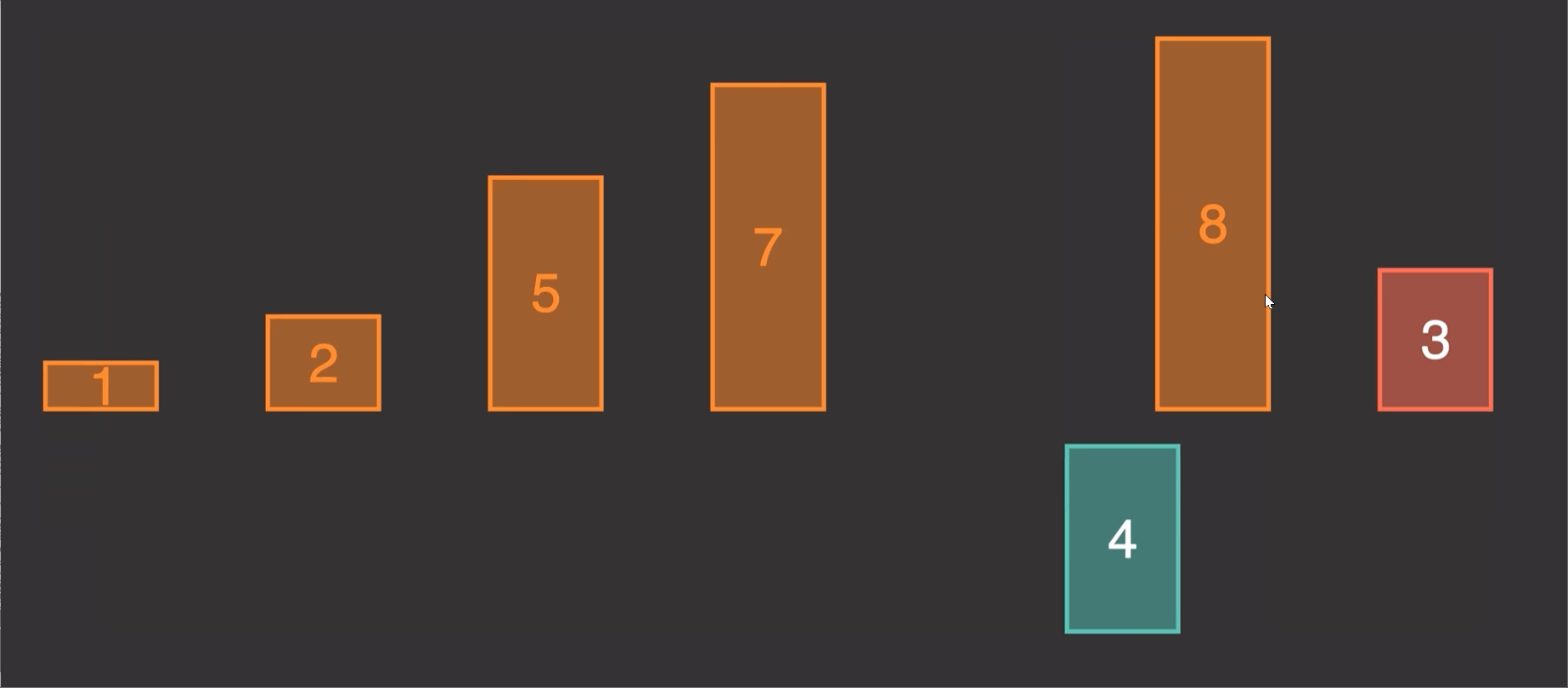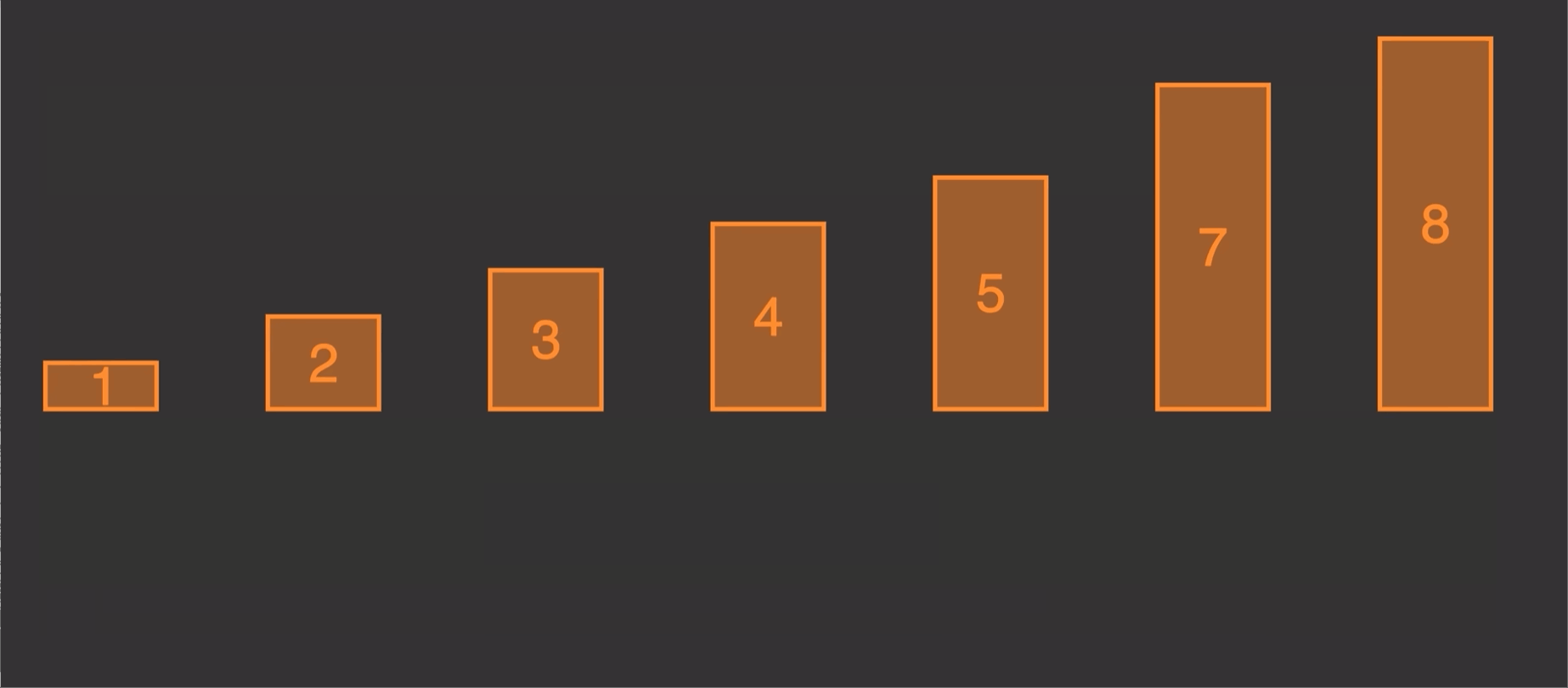
2.2 算法实现
由原理图我们知道这个算法的实现就是第二个先和1第一个比较,调整位置,第三个又和前两个进行比较调整位置。
第一次 调整前两个位置
第二次 调整前三个位置
第三次 调整前四个位置
。。。
n个元素,就调整n-1次
每一次调整,都是倒数一个与倒数第二个比较调整完,倒数第二个又和倒数第三个做比较,知道比较到倒数最后一个也就是最开始的一个。
void InserPort(int* a, int n)
{int i = 0;for (i = 0; i < n - 1; i++)//n个元素调整n-1次{int end = i;int tmp = a[end + 1];//最后一个元素值给tmpwhile (end >= 0){if (tmp < a[end]){//交换a[end + 1] = a[end];a[end] = tmp;}else{//不动break;}//继续比较调整前两个end--;}}
}
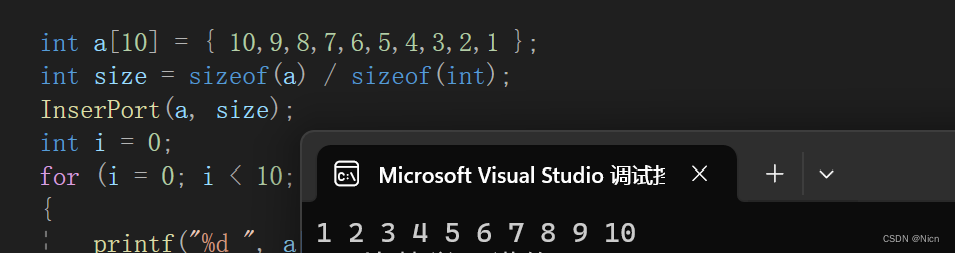
2.3 算法的时间复杂度和空间复杂度分析
上述代码就是最坏的情况:

时间复杂度为O(N^2)
空间复杂度为O(1)
3.希尔排序
3.1算法思想
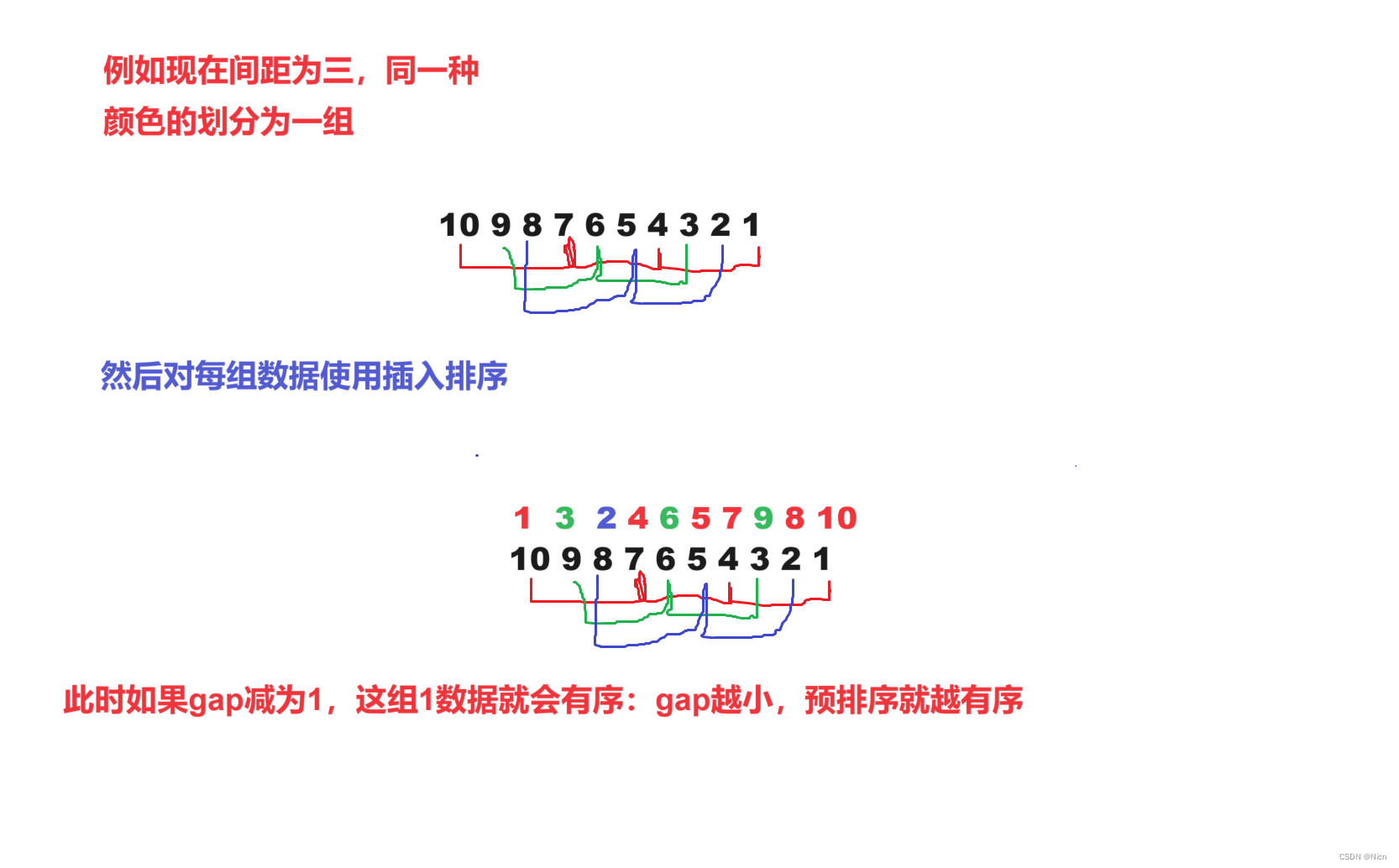
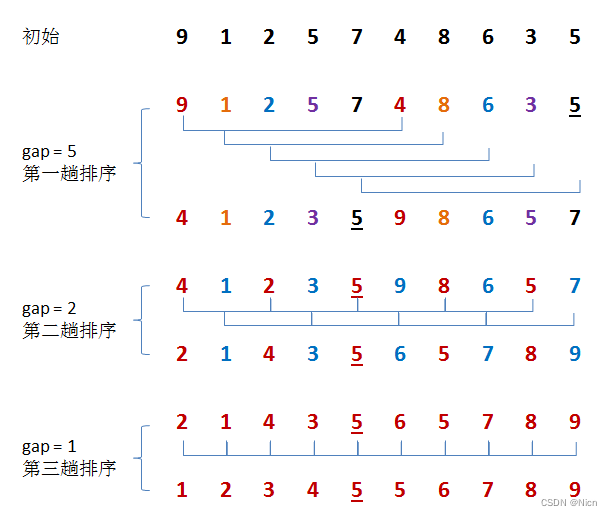
3.2原理演示
3.3代码实现
ShellSort(int* a, int n)
{int i = 0;int gap = n;while (gap > 1){gap /= 2;for (i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end>gap){if (tmp < a[end]){a[end + gap] = a[end];a[end] = tmp;}else{break;}end -= gap;}}}
}3.4希尔算法的时间复杂度

《数据结构》--严蔚敏
 《数据结构-用面相对象方法与C++描述》--- 殷人昆
《数据结构-用面相对象方法与C++描述》--- 殷人昆
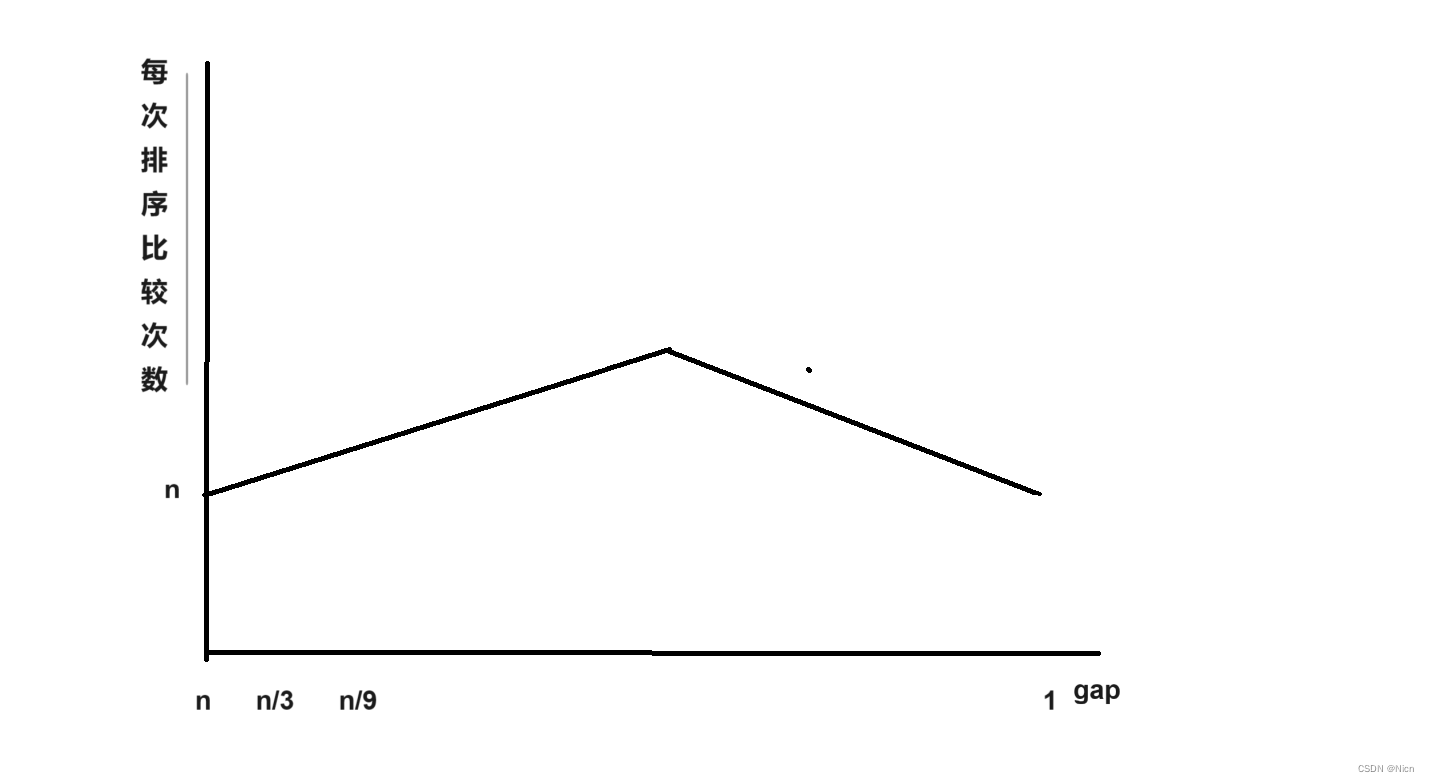
按照: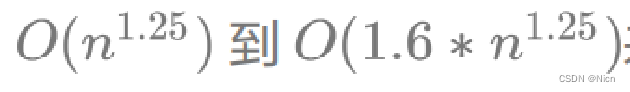
来计算
空间复杂度为O(1)
稳定性:不稳定
4.冒泡排序
核心思想:两两相邻的元素相比较是一种交换排序
4.1冒泡排序原理(图解)

4.2.冒泡排序实现
通过图解原理我们可以发现规律(以10个元素排列举例)
1.每一趟比较完全完成就把这一趟数据的最大数放在最后,第一趟是10个数据中的最大值9在最后,第二趟是9个数据中的8在最后,那么我们10个元素就要循环9趟,那么n个数据,就要循环n - 1趟。
2.第一趟是10个数据,就有9对数据比较,那么第二趟,就有8对数据进行比较。如果一趟有n个数据就要比较n - 1对数据。
3.所以需要两层循环,外层控制趟数,内层控制每一趟要比较的次数。
看如下实现。
int main()
{int len[10] = { 0 };int i = 0;for (i = 0; i < 10; i++){scanf("%d",&len[i]);}int n = sizeof(len) / sizeof(len[0]);//printf("%d", n);int x = 0;for (x = 0; x < n; x++){int y = 0;{for (y = 0; y < n-1 - x; y++){if (len[y] > len[y + 1]){int temp = 0;temp = len[y];len[y] = len[y + 1];len[y + 1] = temp;//交换}}}}int j = 0;for (j = 0; j < 10; j++){printf(" %d ", len[j]);}
}运行结果如图,大家也可以用源码自己体验一下效果:
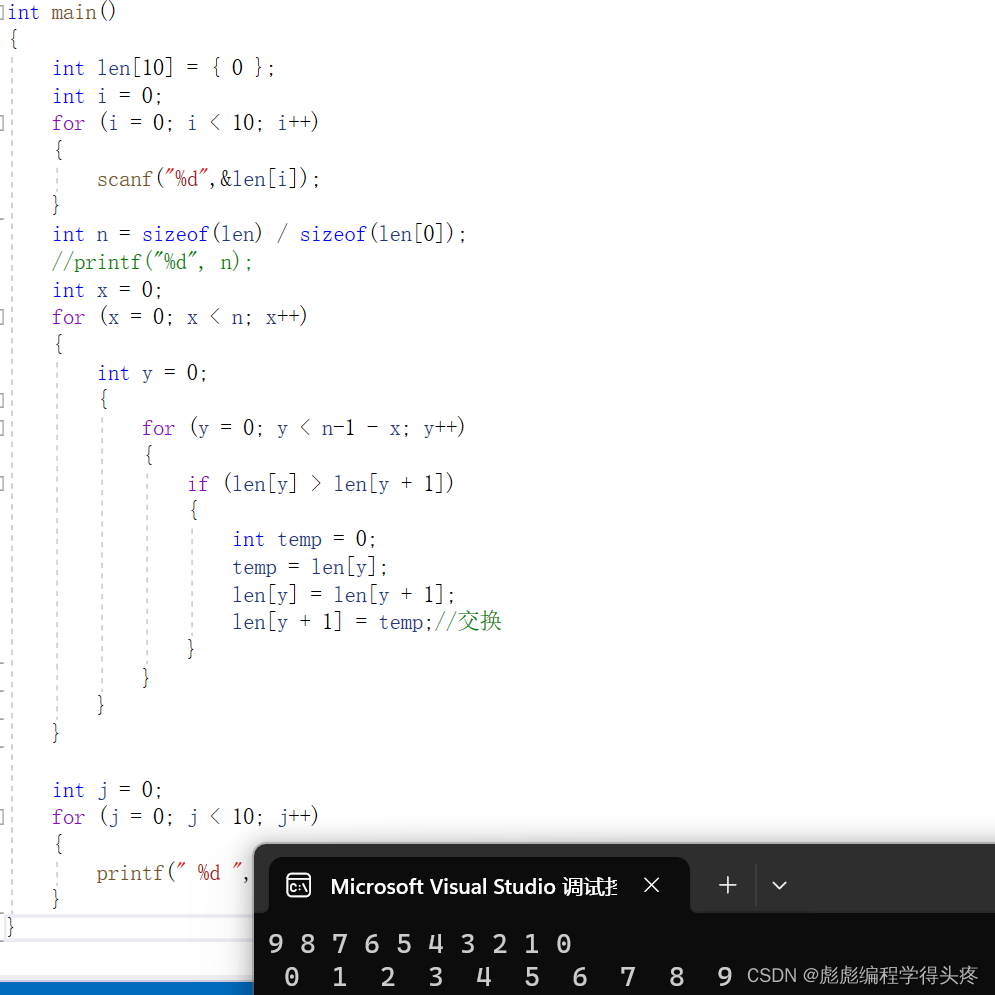
4.3冒泡排序封装为函数
现在已经实现了冒泡排序,为了以后的方便,我们来试着将这个冒泡排序模块功能封装为一个函数。让我们一起来看看自定义为函数有那些坑。
按照上述排序规则和封装函数的方法,我们将数组作为一个函数参数,传递给冒泡排序函数来执行冒泡排序,我们来看一下:
void BBurd_sort(int arr[10])
{int n= sizeof(arr) / sizeof(arr[0]);int x = 0;for (x = 0; x < n; x++){int y = 0;{for (y = 0; y < n - 1 - x; y++){if (arr[y] > arr[y + 1]){int temp = 0;temp = arr[y];arr[y] = arr[y + 1];arr[y + 1] = temp;//交换}}}}}
int main()
{int arr[10] = { 0 };int i = 0;for (i = 0; i < 10; i++){scanf("%d", &arr[i]);}//int sz = sizeof(arr) / sizeof(arr[0]);BBurd_sort(arr);int j = 0;for (j = 0; j < 10; j++){printf(" %d ", arr[j]);}return 0;
}
我们观察到没有发生排序,我们调试看一下:
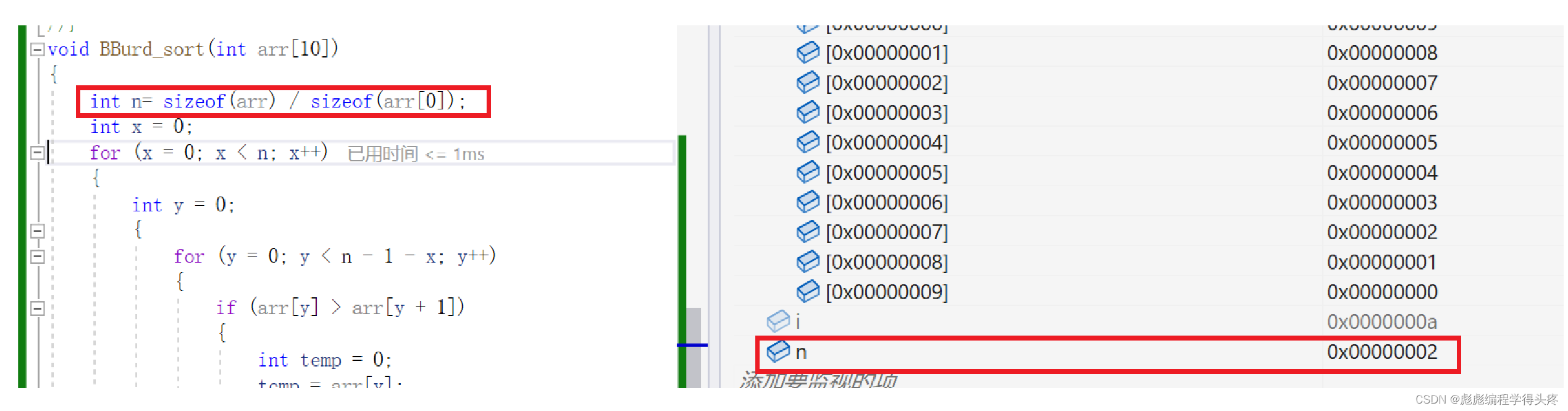
问题所在:我们这里想要实现的功能是n 保存的是数组的大小,那么应该是10才对,为什么是2呢。
思考:sizeof(arr[0] 求的是一个整形数组元素的大小那么其大小就应该是4字节,
那么说明我们的sizeof(arr)就是8字节,那么只有可能我们这里的arr,并不是一整个数组,而是一个地址 (地址也就是指针,在32位操作系统下面大小是4个字节,64位操作系统下是8个字节),那就说明我们这里的arr实质上是一个指针,保存的是数组首元素的地址。
所以在函数里面是没有办法求出这个数组的大小,解决办法,把函数的大小作为一个函数的参数一起传递,看一下改进效果。
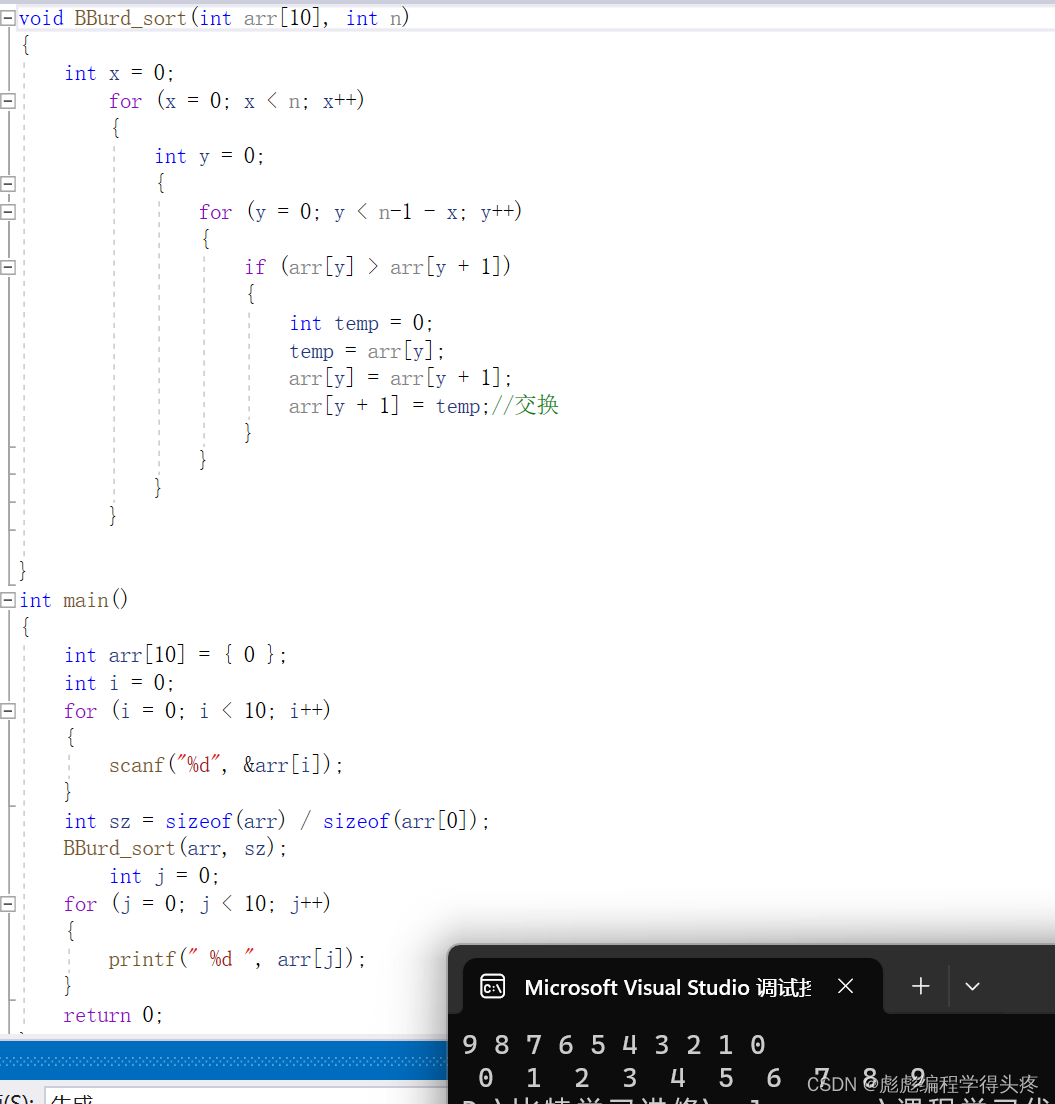
程序正常实现,附上源码。大家体验一下效果。
void BBurd_sort(int arr[10], int n)
{int x = 0;for (x = 0; x < n; x++){int y = 0;{for (y = 0; y < n-1 - x; y++){if (arr[y] > arr[y + 1]){int temp = 0;temp = arr[y];arr[y] = arr[y + 1];arr[y + 1] = temp;//交换}}}}}
int main()
{int arr[10] = { 0 };int i = 0;for (i = 0; i < 10; i++){scanf("%d", &arr[i]);}int sz = sizeof(arr) / sizeof(arr[0]);BBurd_sort(arr, sz);int j = 0;for (j = 0; j < 10; j++){printf(" %d ", arr[j]);}return 0;
}4.4 冒泡排序代码效率改进。
思考:
对于这样一个有序数列,我们如果执行的话,我们的自定义函数就还是会跑一遍,那么这样实际效率并不高。所以想能不能改进一下我我们的代码。

再次浏览原理图,我们不难发现这样一个规律,只要数据是乱序一趟下来就会有元素在发生交换。
比如:
9 1 2 3 4 5 6 7 8
这样的数据,第一趟会有元素交换,第二趟就没有。
那么我们可以这样,只要某一趟没有交换,说明此时我们的数列已经有序了就跳出
只要发生交换就继续。
那么看一下改进代码:
void BBurd_sort(int arr[10], int n)
{int x = 0;for (x = 0; x < n; x++){int flag = 0;int y = 0;for (y = 0; y < n-1 - x; y++){if (arr[y] > arr[y + 1]){int temp = 0;temp = arr[y];arr[y] = arr[y + 1];arr[y + 1] = temp;//交换flag = 1;//发生了交换就改变flag}}//执行完一趟就判断一下有没有交换,有交换就继续,没有交换就直接退出,不用排序了if (flag == 0){break;}}}
int main()
{int arr[10] = { 0 };int i = 0;for (i = 0; i < 10; i++){scanf("%d", &arr[i]);}int sz = sizeof(arr) / sizeof(arr[0]);BBurd_sort(arr, sz);int j = 0;for (j = 0; j < 10; j++){printf(" %d ", arr[j]);}return 0;
}5.堆排序
使用堆结构对一组数据进行排序,方便对数据进行处理。粗暴办法就是将原数组数据插入堆,再取堆数据覆盖,这种方法首先得有堆结构,其次插入数据就要额外开辟空间。
最好的方式就是直接将原数组或者原来的这组数据变成堆。将原数组直接看成一颗完全二叉树,一般都不是堆。那么就要将原数据之间调成堆----建堆
建堆不是插入数据,只是使用向上调整的思想。在原有数据上进行更改,调换。
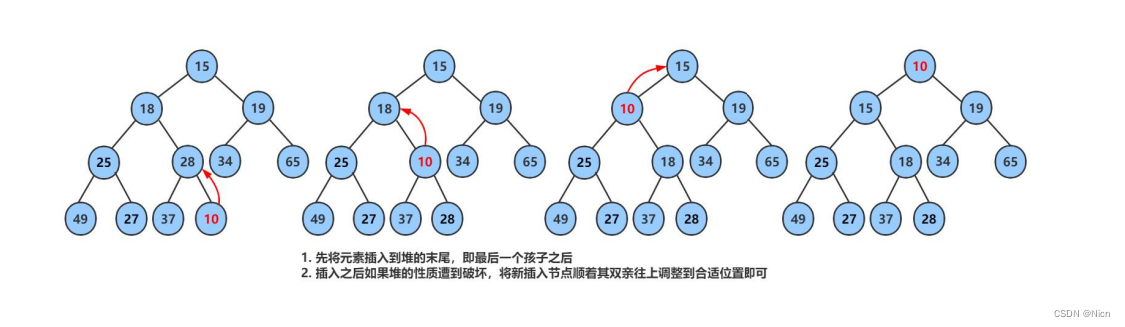
5.1升序建大堆,降序建小堆
一般我们要利用堆结构将一组数据排成升序,就建立大堆
要利用堆结构将一组数据排成降序,就建立小堆。
void HeapSort(int* a, int n)
{//对数据进行建堆for (int i = 0; i < n; i++){AdjustUp(a, 1);}//堆排序---向下调整的思想int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;//让n-1个数据调整成堆选出次小}}5.2 建堆的时间复杂度
5.2.1 向下调整建堆
讨论最坏的时间复杂度
将下图进行建立一个大堆
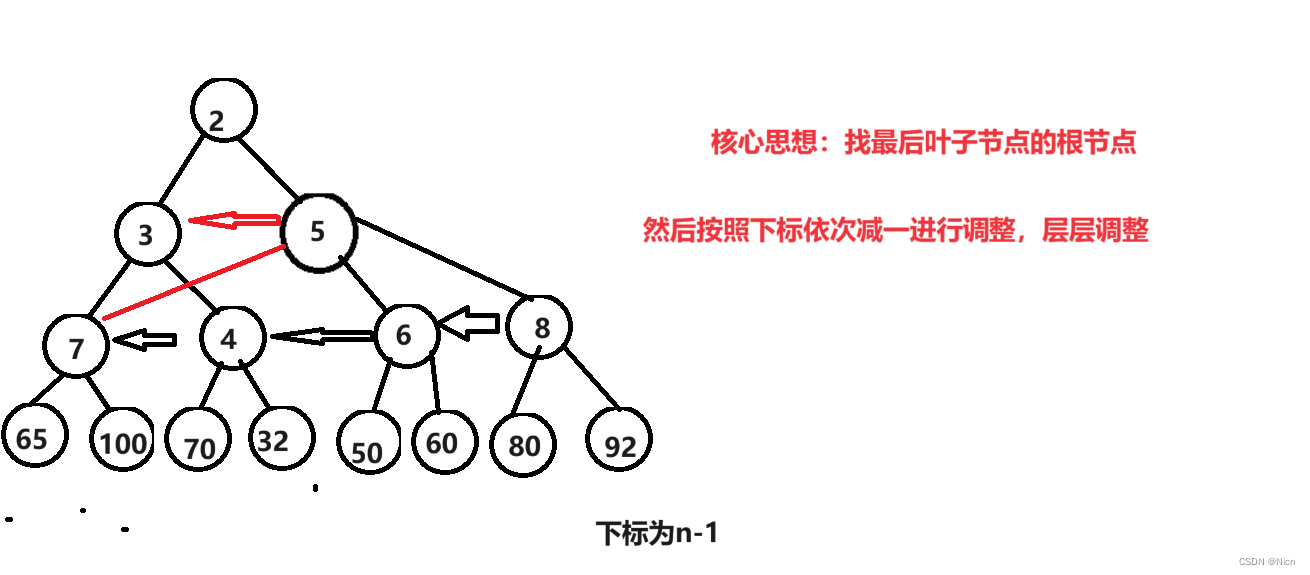
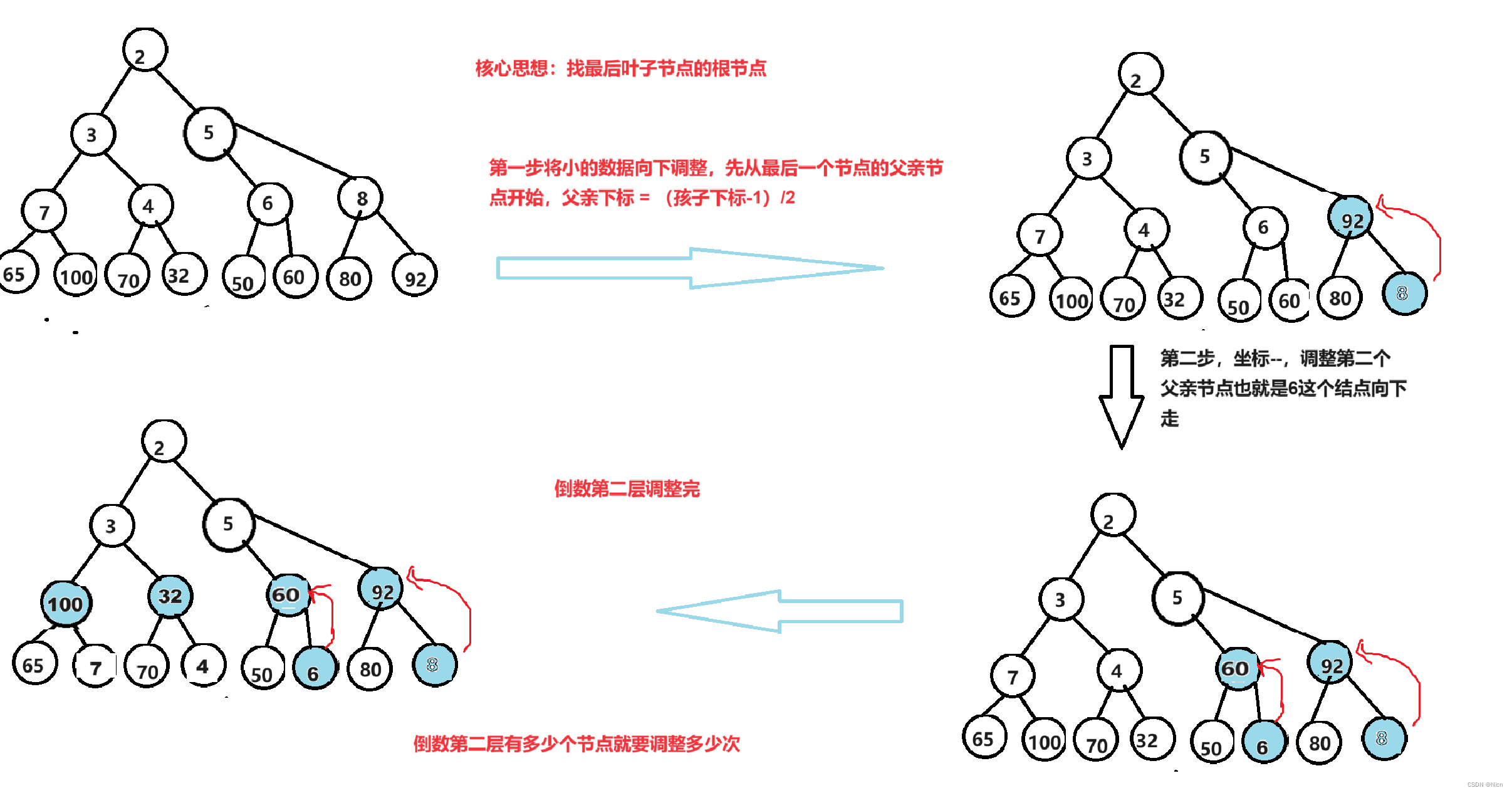
实现:
void AdjustDown(int* a, int parent, int n)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] < a[child + 1]){child++;//找出左右孩子中大的一个1}if (a[child] >a[parent]){//交换Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
//堆排序//首先将数据建堆//升序建大堆,降序建小堆//采用向下调整建堆的方式时间复杂度较小int child = n - 1;int parent = (child - 1) / 2;while (parent >=0){AdjustDown(a, parent, n);parent--;}假设有h层,这里测算的时间复杂度是最坏的情况,那么就相当于调整的是一个满二叉树的堆。
第h层 ,共有2^(h-1)个节点, 需要调整0次
第h-1层,共有2^(h-2)个节点 ,每个节点调整一次,调整:2^(h-2)*1次
第h-2层,共有2^(h-3)个节点,每个节点最坏向下调整两次,调整2^(h-3)*2次
:
:
:
第3层,共有2^(2)个节点,每个节点向下调整h-3次,调整2^(2)*(h-3)次
第2层,共有2^(1)个节点,每个节点向下调整h-2次,调整2^(1)*(h-2)次
第1层,共有2^(0)个节点,每个节点向下调整h-1次,调整2^(0)*(h-1)次
时间复杂度为:
T(h) = 2^(0)*(h-1)+2^(1)*(h-2)+2^(2)*(h-3)+…………2^(h-3)*2+2^(h-2)*1①
2T(h) = 2^(1)*(h-1)+2^(2)*(h-2)+2^(3)*(h-3)+…………2^(h-2)*2+2^(h-1)*1
②
②-①得
T(h) = 2^(1)+2^(2)……+2^(h-2)+2^(h-1)+1-h
=2^0+2^(1)+2^(2)……+2^(h-2)+2^(h-1)-h
=2^h-1-h
由于h是树的层高,与节点个数的关系是:N = 2^h-1
h = log(n+1)
所以时间复杂度为:
O(N) = N-longN+1~O(N)
5.2.2向上调整建堆

假设有h层,这里测算的时间复杂度是最坏的情况,那么就相当于调整的是一个满二叉树的堆。
第2层,共有2^1个节点,每个节点向上调整1次
第3层,共有2^2个节点,每个节点向上调整2次
:
:
:
第h-2层,共有2^(h-3)个节点,每个节点向上调整h-3次
第h-1层,共有2^(h-2)个节点,每个节点向上调整h-2次
第h层 ,共有2^(h-1)个节点,每个节点向上调整h-1次
时间复杂度为:T(h) = 2^1*1+2^2*2+2^3*3……2^(h-3)*(h-3)+2^(h-2)*(h-2)+2^(h-1)*(h-1)
2 T(h) = 2^2*1+2^3*2+2^4*3……2^(h-2)*(h-3)+2^(h-1)*(h-2)+2^(h)*(h-1)
T(h) = -2-(2^2+2^3+2^4…………2^(h-1))+2^h(h-1)
= -(2^0+2^1+2^2…………2^(h-1))+2^h(h-1)+2^0
=2^h*(h-2)+2
由于h是树的层高,与节点个数的关系是:N = 2^h-1
h = log(n+1)
T(N) = (N+1)log(N+1)-2N-1
5.3 排序实现
排序和删除的原理是一样的,先找最大/最小然后次大/次小,每次选取数据后不会将后面数据覆盖上来,否则就会导致关系全乱,可能次大数据就要重新建堆,增加了工作量了。而是通过堆顶元素和最后一个数据交换位置过后,向下调整思想,将排除刚刚调整的尾部最大数据除外的剩下数据看成堆,循环排序。
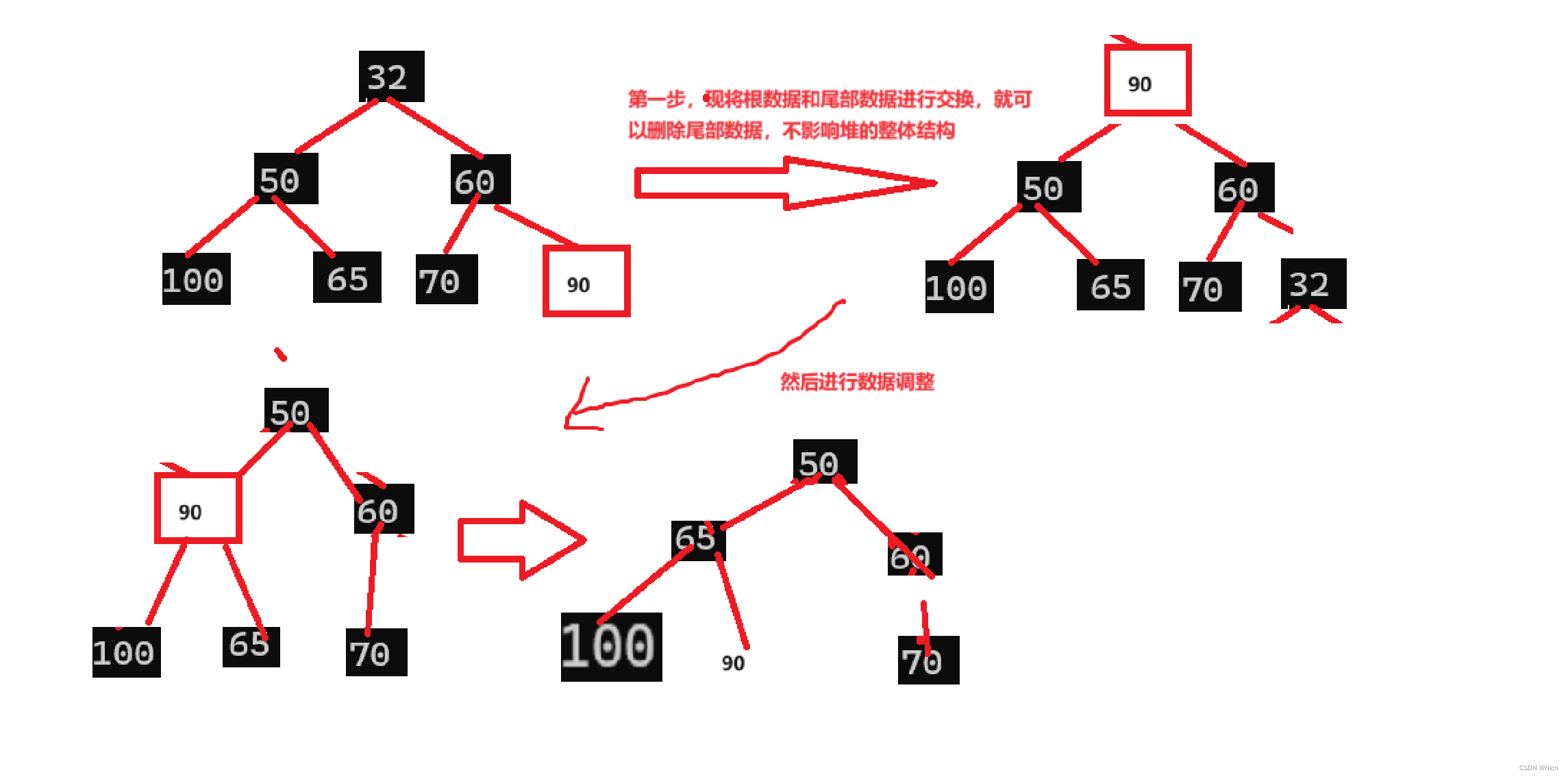
最后发现:大堆这样处理的数据最大的数据在最后,最小的在最前,小堆相反。
void AdjustDown(int* a, int parent, int n)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] < a[child + 1]){child++;//找出左右孩子中大的一个1}if (a[child] >a[parent]){//交换Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
//堆排序void HeapSort(int* a, int n)
{//首先将数据建堆//升序建大堆,降序建小堆//采用向下调整建堆的方式时间复杂度较小int child = n - 1;int parent = (child - 1) / 2;while (parent >=0){AdjustDown(a, parent, n);parent--;}//排序int end = n - 1;while (end >= 0){Swap(&a[0], &a[end]);AdjustDown(a, 0, end);end--;}}6.选择排序
6.1基本思想:
6.2算法演示

6.3代码实现
//选择排序void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin <end){int min = begin;int max = begin;int i = 0;for (i = begin+1; i <= end; i++){if (a[min] > a[i]){min = i;}if (a[max] < a[i]){max = i;}}Swap(&a[begin], &a[min]);if (begin == max){max = min;}Swap(&a[end], &a[max]);end--;begin++;}}
6.4时间复杂度分析
如果有10个数据: 10 9 8 7 6 5 4 3 2 1第一次:比较2(n-1次)第二次比较:2(n-3)次最后一次比较:1次总共比较:n/2次,时间复杂度为:1/4n^2
7.快速排序
算法思想:
7.1 hoare版本
单趟:
7.1.1算法图解
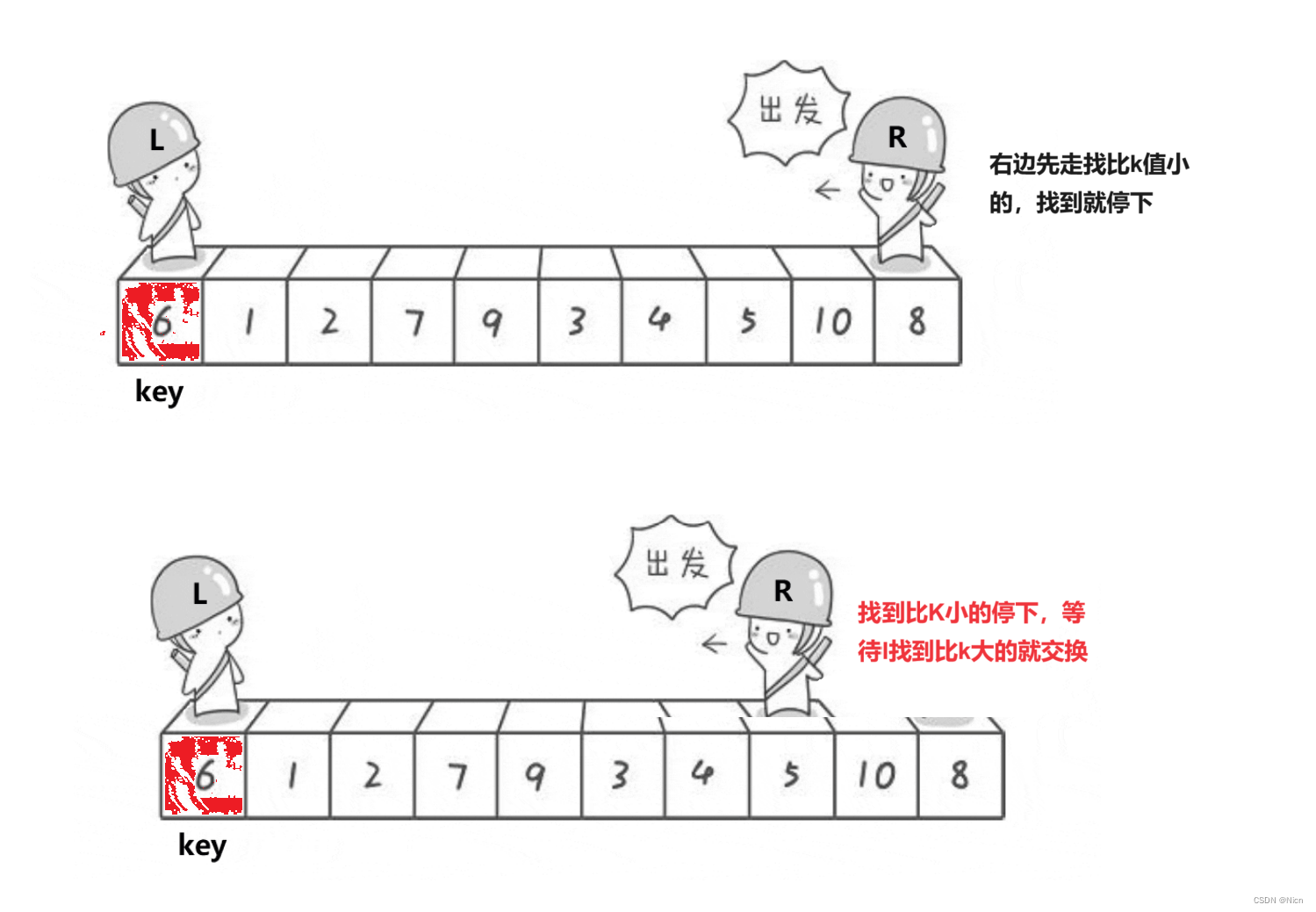
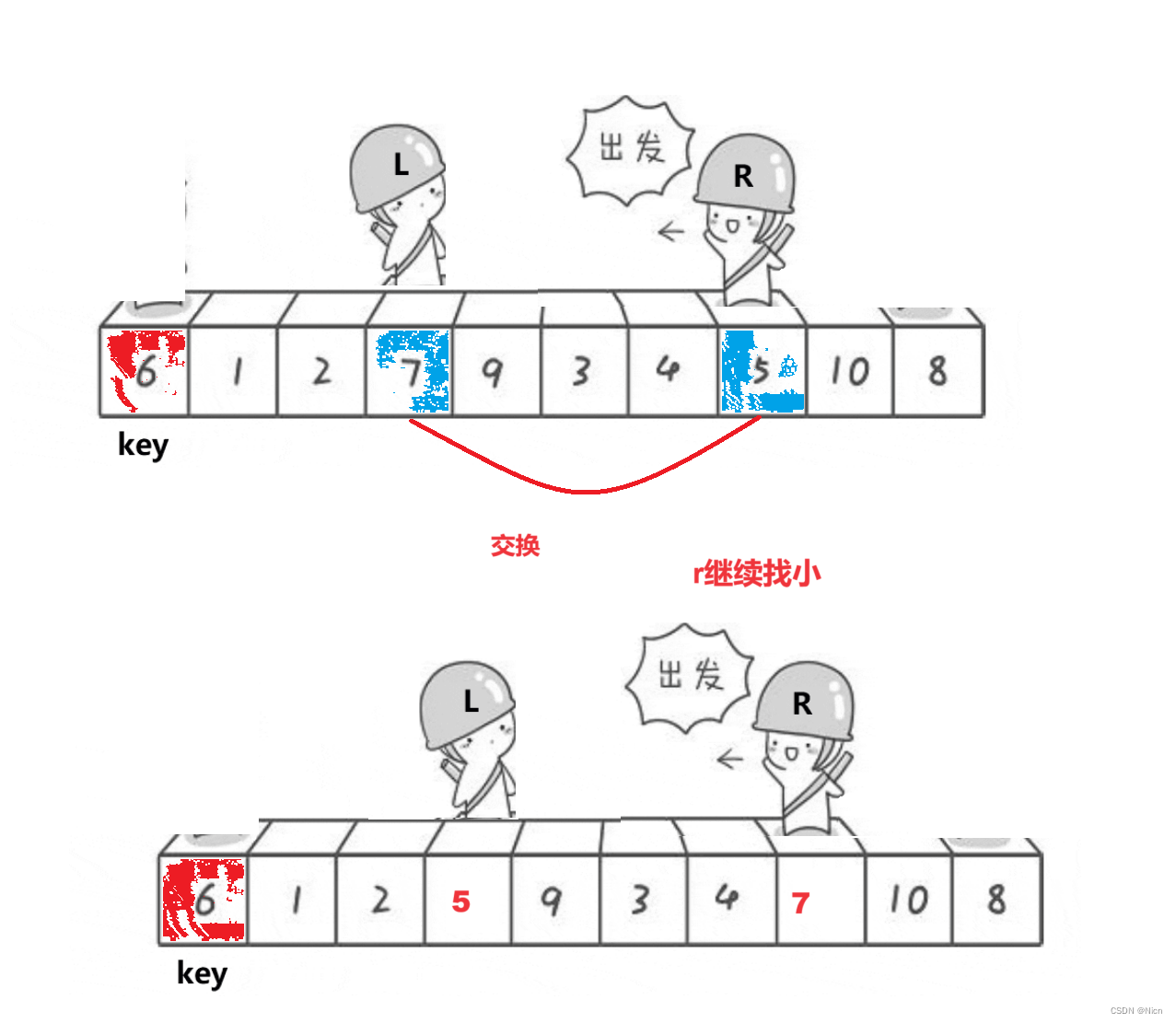
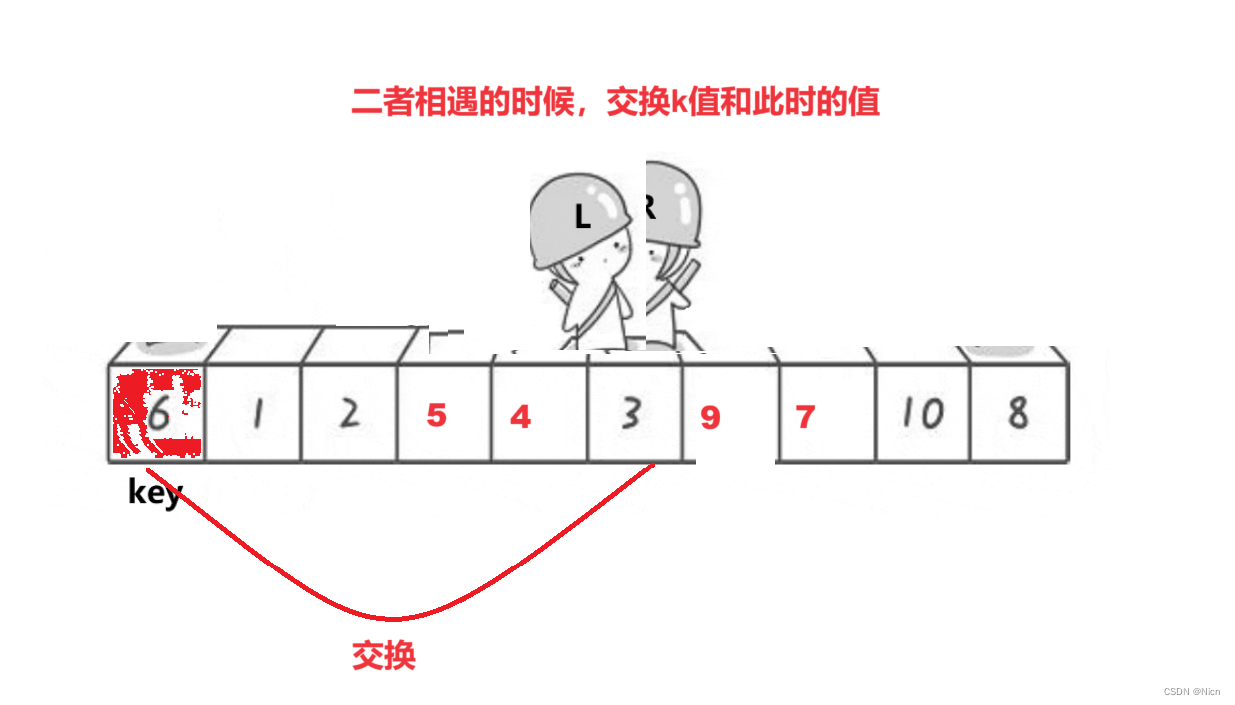
为什么相遇的位置一定是比k值小的值是因为右边先走,那么每次左边停下来的值经过交换一定是比k值大,此时r继续走,找到比k值大的数才会停下来,所以如果右边先走,停下来的地方值一定小于k,如果左边先走,停下来的地方的值一定大于k。
将上述过程递归就可以得到一个有序的序列:

7.1.2代码实现
int Partsort(int* a, int left, int right)
{int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){right--;//如果左右两边同时是key,此时如果不取等号就回陷入死循环//再次判断left<key是因为值都比k大或者都比k小的极端情况出现越界问题,因为外层循环只判断了一次,里面的--++的循环没有判断}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}//快速排序
void QuickSort(int* a, int left,int right)
{if (left >= right){//大于为空,等于只有一个值return;}int keyi = Partsort(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}7.1.3 算法优化---三数取中
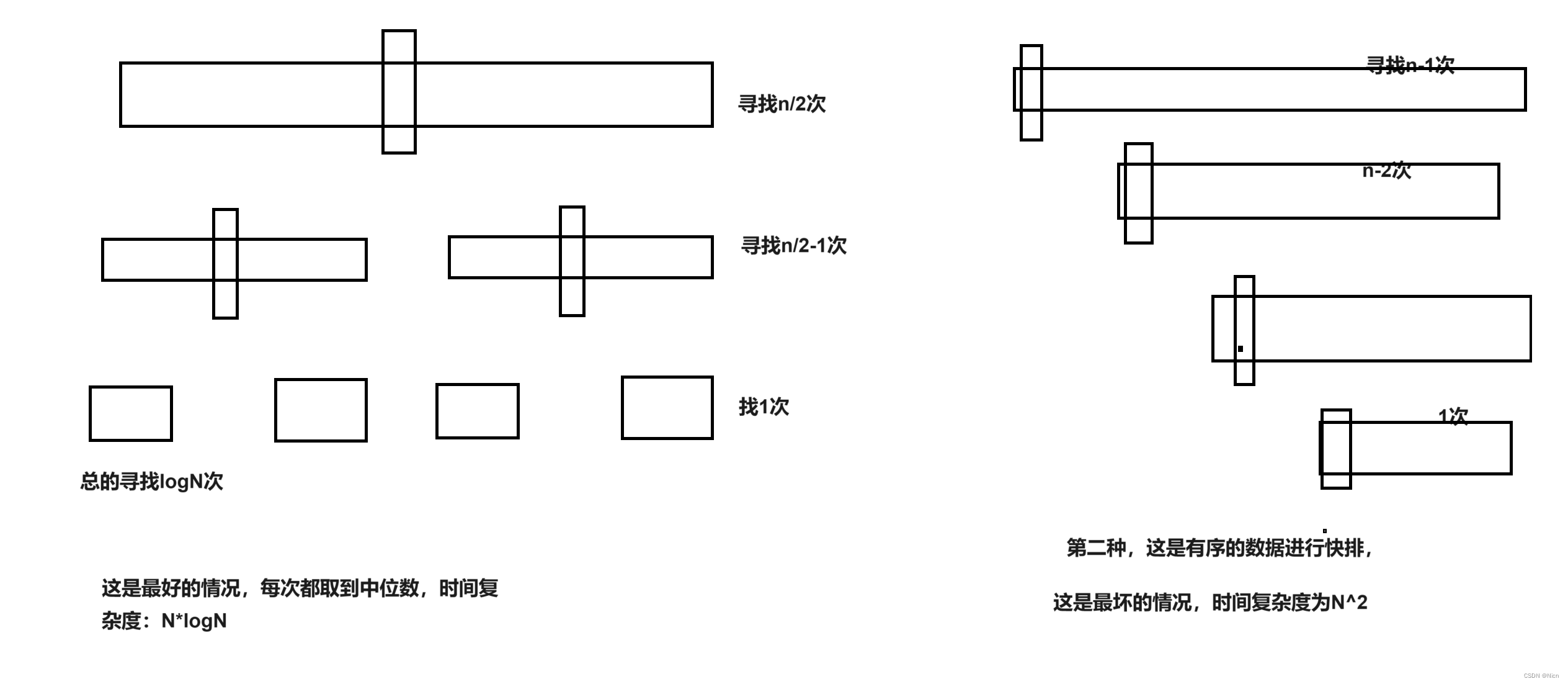
为了保证我们快排的效率呢,我们试着调整一下我们选择key值的策略。
每次选取三个数中中间值的一个作为我们的key,并且将这个值换到数组的最左边:
int GetMid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else{if (a[mid > a[right]]){return mid;}else if (a[left] < a[right])//mid是最小的{return left;}else{return right;}}
}
int Partsort(int* a, int left, int right)
{int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){right--;//如果左右两边同时是key,此时如果不取等号就回陷入死循环//再次判断left<key是因为值都比k大或者都比k小的极端情况出现越界问题,因为外层循环只判断了一次,里面的--++的循环没有判断}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}//快速排序
void QuickSort(int* a, int left,int right)
{if (left >= right){//大于为空,等于只有一个值return;}int keyi = Partsort(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}这样我们的逆序排序这种对于快排最坏的情况就变成最好的情况,十万个数据1毫秒就可以排好。
7.2挖坑法快排
7.2.1算法图解
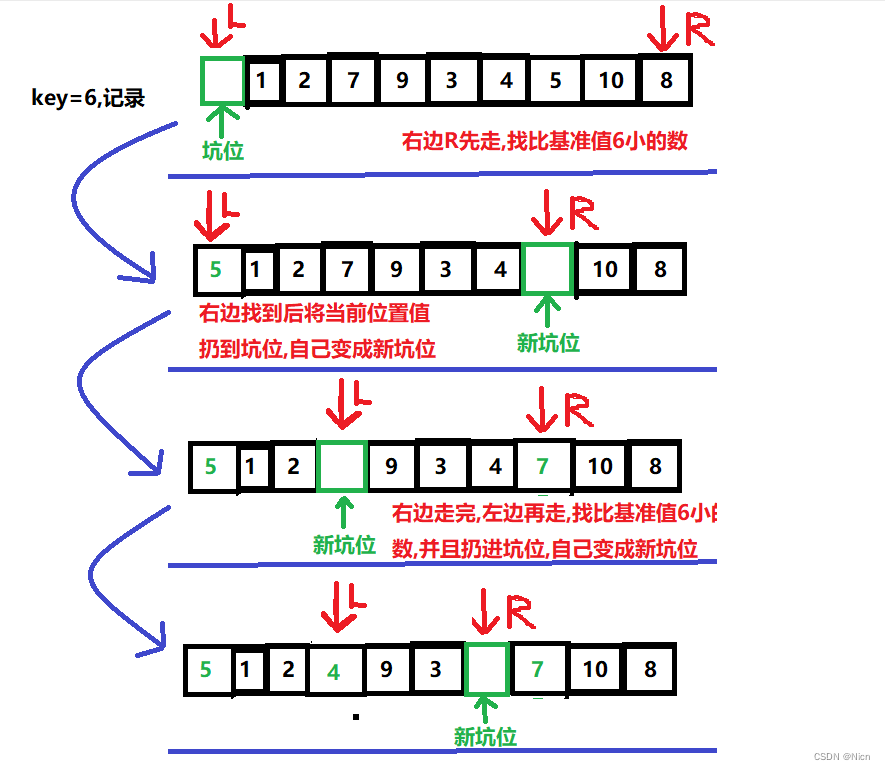
7.2.2 代码实现
//挖坑法
int Partsort2(int* a, int left, int right)
{int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);int ken = a[left];int hole = left;while (left < right){while (left < right && a[right] >= ken){right--;}a[hole] = a[right];hole = right;while (left < right && a[left] <= a[ken]){left++;}a[hole] = a[left];hole= left;}a[hole] = ken;return hole;}
7.3 前后指针法
逻辑:cur找比key值小的值,然后prev遇到比key值大的就停下来,直到cur遇到比key值小的值过后就交换。
prev:
在cur没有遇到比key值大的值的时候,prev紧紧的跟着cur
在cur遇到比key值大的值的时候,prev就停下来了,prev在比key大的一组值的前面。
//前后指针
int Partsort3(int* a, int left, int right)
{int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int prev = left;int cur = prev + 1;while (cur <= right){if (a[cur] < a[keyi]&&prev++ != cur)//防止开始位置自己跟自己交换{Swap(&a[prev++], &a[cur]);}cur++;}Swap(&a[prev], &a[keyi]);return prev;}7.4快速排序进一步优化
按照上面的方法实际主题来说,大思想就是递归,递归是有消耗的,而且,最后几层的递归往往是最大的,如果当递归区间的数值减少到一定程度,我们就不递归了,特别是到最后一两层的时候,那么排序的效率就会有提升。
//快速排序
void QuickSort(int* a, int left,int right)
{if (left >= right){//大于为空,等于只有一个值return;}if ((right - left + 1) > 10){int keyi = Partsort(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}else{InserPort(a + left, right - left + 1);}
}
小区间优化,编译器对递归优化也比较好,小区间不在递归,降低递归次数
7.5快速排序非递归写法
使用栈保存每次划分的区间
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (StackEmpty(&st) != 0)
{right = StackTop(&st);StackPop(&st);left = StackTop(&st);StackPop(&st);if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)StackPush(&st, div+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, div);
}StackDestroy(&s);
} 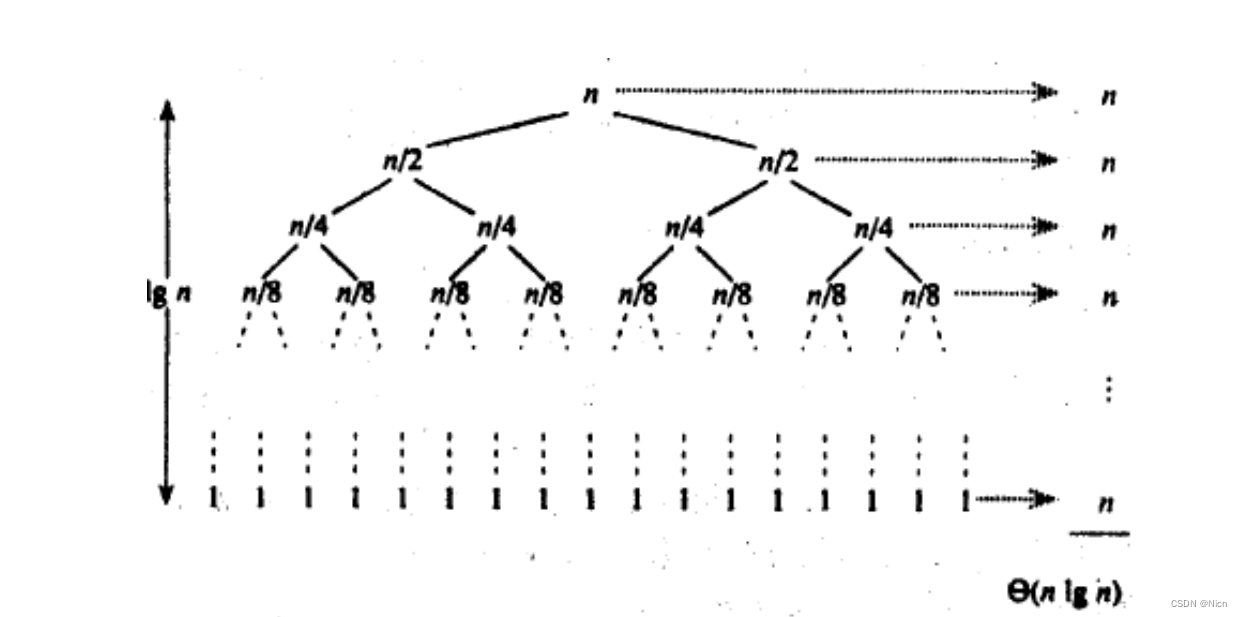
8.归并排序
8.1排序思想:
8.2 算法图解

void _MergeSort(int* a, int* tmp,int begin,int end)
{if (end <= begin){//递归到只有一个或者没有就返回return;}//分割int mid = (end +begin) / 2;//没有那么均分也不是很影响//然后对左右区间进行递归操作 左区间:[begin mid] [mid+1,end}_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid + 1, end);//归并到tmp数组里面,再拷贝回原数组int begin1 = begin, end1 = mid;//左区间int begin2 = mid + 1, end2 = end;//右区间int index = begin;//tmo数组中的对应位置while (begin <= end1 && begin2 <= end2)//需要同时将左右两边小的拿出来插入到tmp数组{if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++ ];//往后继续找,直到一个区间遍历完}else{tmp[index++] = a[begin2++];}}//出循环,有一边区间肯定遍历完了,但是不确定是那个区间while (begin1 <= end1){tmp[index++] = a[begin1++];//这种情况是左边区间没有遍历完,将后续数据放在这个区间的后面}while (begin2 <= end2){tmp[index++] = a[begin2++];//这种情况是右边区间没有遍历完,将后续数据放在这个区间的后面}//将tmp数组归并回原数组的对应位置,所以不一定是从0开始拷贝的memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));//a+begin tmp+begin表示当前区间的起始位置//end -begin+1
}
//归并排序
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);//为归并区间开辟存储数据的数组,空间复杂度产生于此if (tmp == NULL){perror("malloc");exit(-1);}//区间分割//递归不能每次都开辟空间,所以这里分离出子函数_MergeSort(a,tmp, 0, n - 1);free(tmp);tmp = NULL;
}8.3 归并排序非递归实现
//归并排序非递归版本
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);//为归并区间开辟存储数据的数组,空间复杂度产生于此if (tmp == NULL){perror("malloc");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//[begin1,end][begin2,end2]归并int index = i;//tmo数组中的对应位置while (begin1 <= end1 && begin2 <= end2)//需要同时将左右两边小的拿出来插入到tmp数组{if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];//往后继续找,直到一个区间遍历完}else{tmp[index++] = a[begin2++];}}//出循环,有一边区间肯定遍历完了,但是不确定是那个区间while (begin1 <= end1){tmp[index++] = a[begin1++];//这种情况是左边区间没有遍历完,将后续数据放在这个区间的后面}while (begin2 <= end2){tmp[index++] = a[begin2++];//这种情况是右边区间没有遍历完,将后续数据放在这个区间的后面}//将tmp数组归并回原数组的对应位置,所以不一定是从0开始拷贝的memcpy(a + i, tmp + i, (2 * gap) * sizeof(int));//a+begin tmp+begin表示当前区间的起始位置//end -begin+1 }gap *= 2;}free(tmp);tmp = NULL;
}
这个代码当数据为偶数个的时候就会越界
奇数个二二归的时候也会越界,需要修正。
8.4归并排序的特性总结:
9.计数排序
9.1算法思想:
9.2 算法演示:
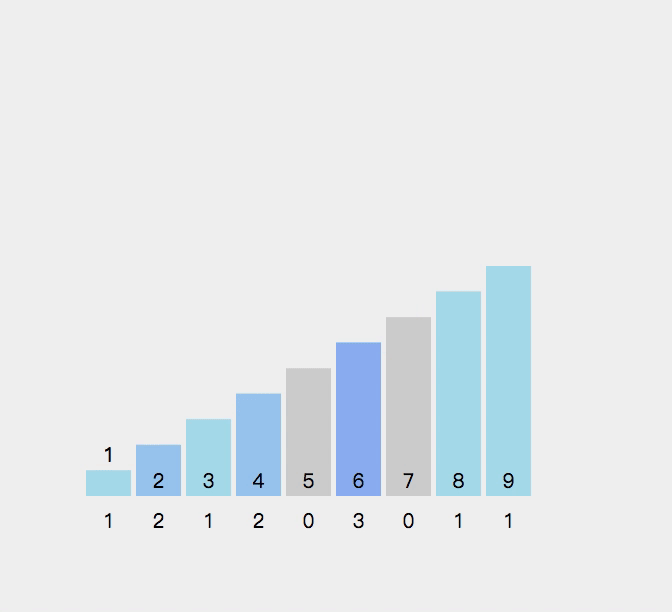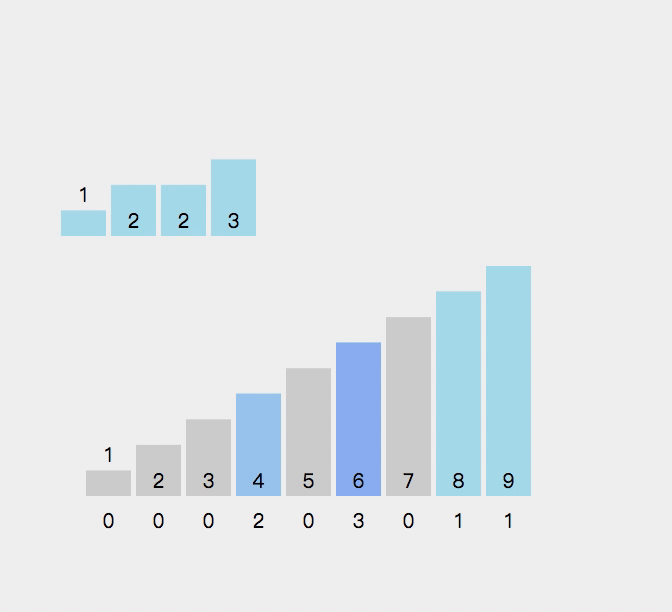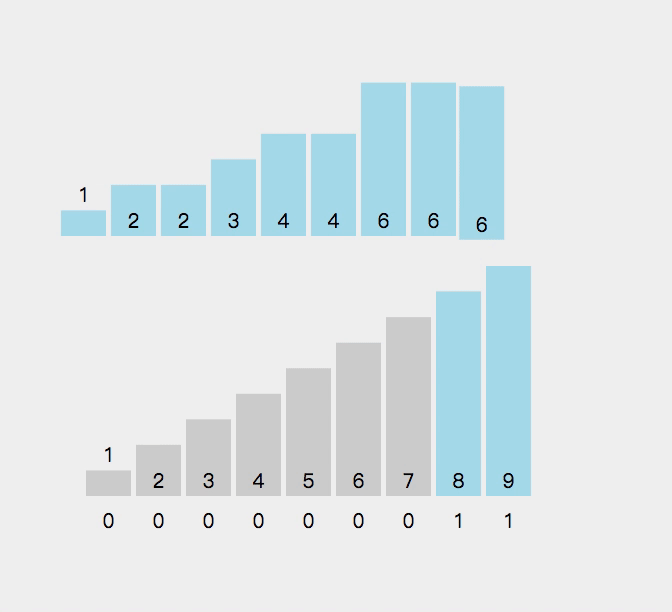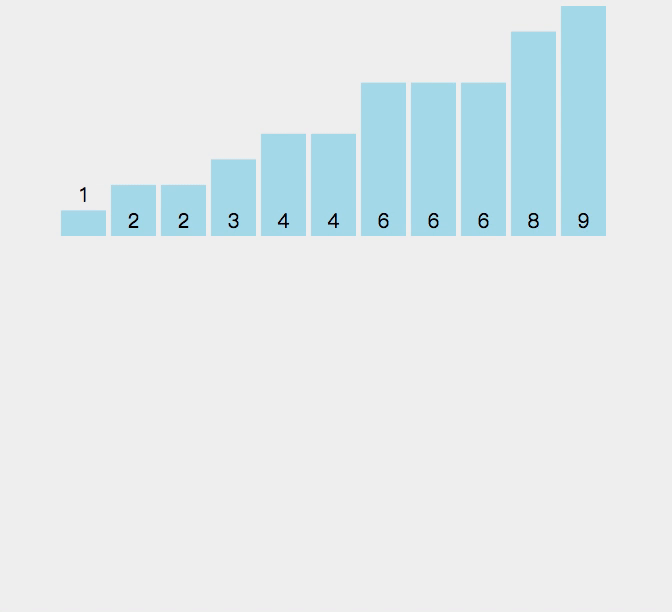
//计数排序
void MergeSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 0; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);//统计数据出现的个数for (int i = 0; i < n; i++){count[a[i] - min]++;}//排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}
9.3计数排序的特性总结:
- 1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 2. 时间复杂度:O(MAX(N,范围))
- 3. 空间复杂度:O(范围)
- 4. 稳定性:稳定
10.结语
以上就是本期所有内容,耗时半周,应该整理得比较全面,越往后面的排序代码实现就越难。知识含量蛮多,大家可以配合解释和原码运行理解。创作不易,大家如果觉得还可以的话,欢迎大家三连,有问题的地方欢迎大家指正,一起交流学习,一起成长,我是Nicn,正在c++方向前行的奋斗者,数据结构内容持续更新中,感谢大家的关注与喜欢。
相关文章:
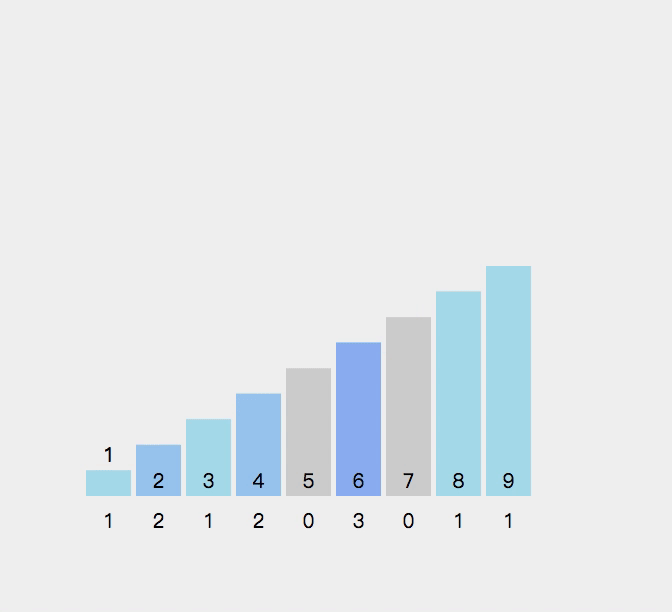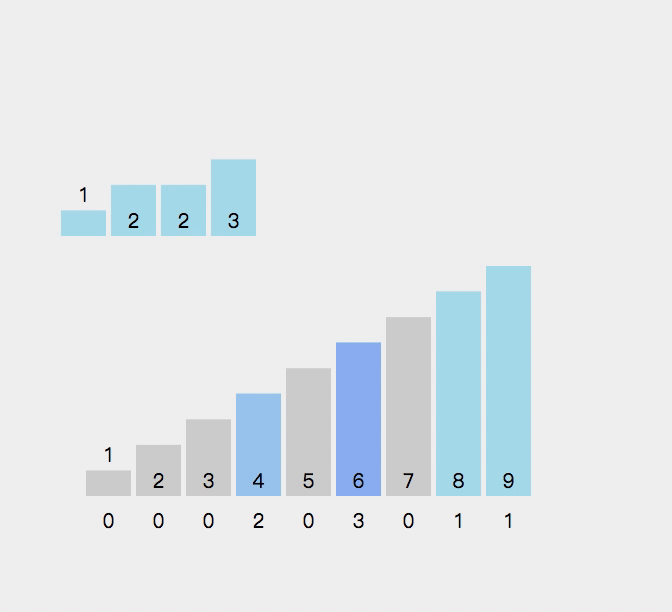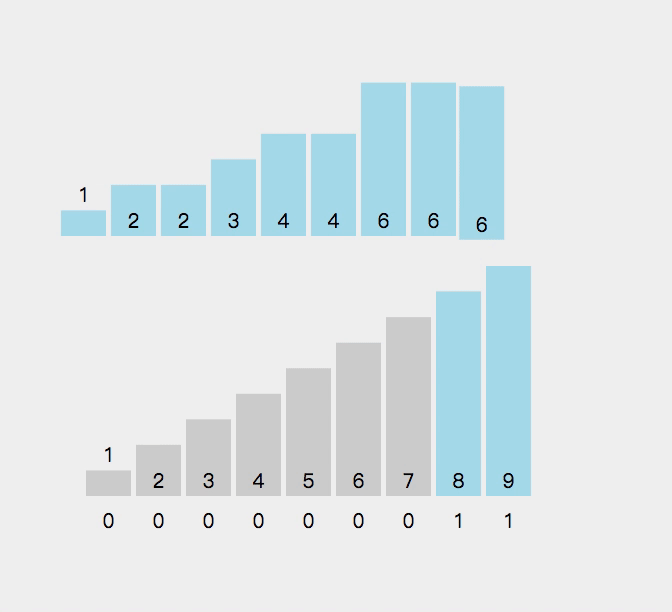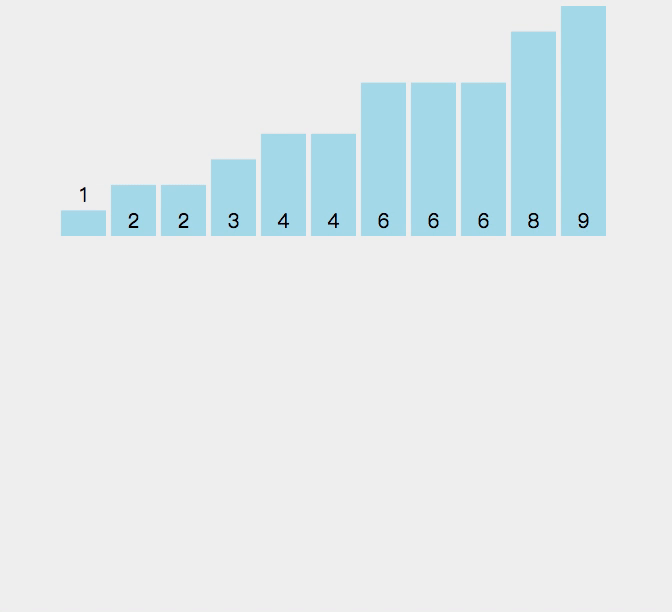
【数据结构与算法初阶(c语言)】插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序、计数排序-全梳理(万字详解,干货满满,建议三连收藏)
目录 1.排序的概念及其运用 1.1排序的概念 1.2排序运用 1.3常见的排序算法 2.插入排序 2.1 原理演示:编辑 2.2 算法实现 2.3 算法的时间复杂度和空间复杂度分析 3.希尔排序 3.1算法思想 3.2原理演示 3.3代码实现 3.4希尔算法的时间复杂度 4.冒泡排序 4.1冒泡排…...
[蓝桥杯 2019 省赛 AB] 完全二叉树的权值
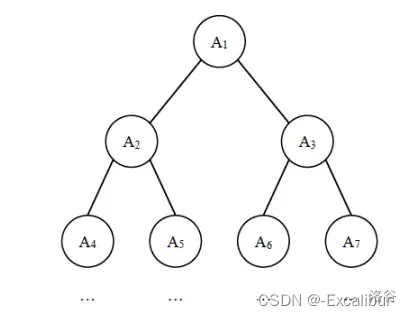
# [蓝桥杯 2019 省 AB] 完全二叉树的权值 ## 题目描述 给定一棵包含 $N$ 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 $A_1,A_2, \cdots A_N$,如下图所示: 现在小明要把相同深度的节点的权值…...
亮数据Bright Data,引领高效数据采集新体验
随着互联网和大数据的日益普及,我们对于高速、安全和无限畅通的网络体验追求越发迫切,随之而来的网络安全和隐私保护变得越来越重要。IP代理作为一种实用的代理工具,可以高效地帮我们实现网络数据采集,有效解决网络安全问题&#…...

C#学习笔记
一、事件派发器 在C#中,事件派发器通常是指事件委托和事件处理程序的组合,用于实现一种观察者设计模式。它允许对象在状态发生变化时通知其他对象,从而实现对象之间的解耦。 事件派发器的基本组成部分: 事件委托(Ev…...
【A-006】基于SSH的新闻发布系统(含论文)
【A-006】基于SSH的新闻发布系统(含论文) 开发环境: Jdk7(8)Tomcat7(8)MySQLIntelliJ IDEA(Eclipse) 数据库: MySQL 技术: SpringStruts2HiberanteJSPJquery 适用于: 课程设计,毕业设计&…...
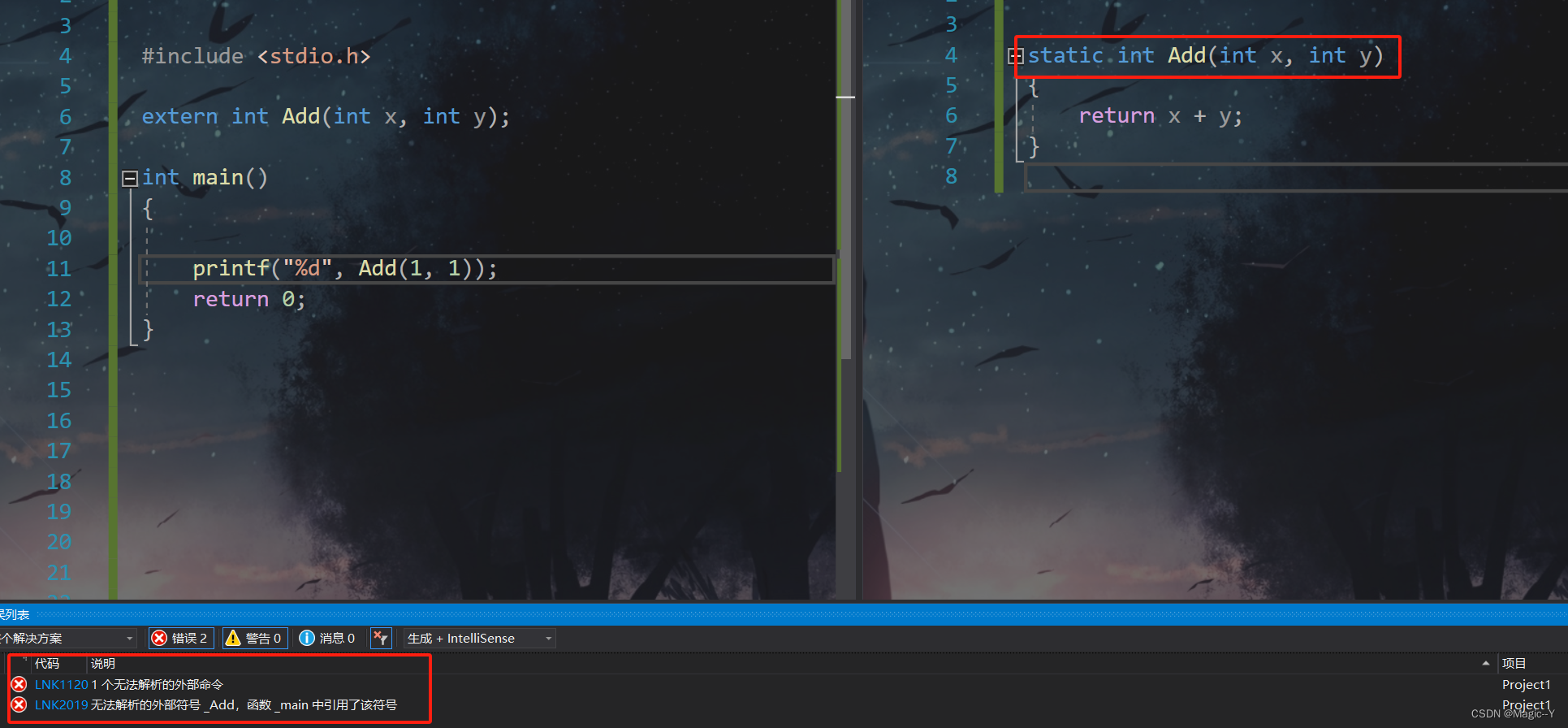
c语言-static
static作用:修饰变量和函数 修饰局部变量-静态局部变量 static未修饰局部变量 #include <stdio.h>void print() {int a 0;a;printf("%d ", a); }int main() {int i 0;for (i 0; i < 10; i){print();}return 0; }运行结果 static修饰局部变…...

zuul的性能调优
文章目录 zuul的性能调优Zuul参数剖析semaphore(信号量)ribbonhystrix高并发下常见Zuul异常熔断 zuul 1.x 与2.x的区别与总结 zuul的性能调优 在项目实践中,使用jemeter多线程并发访问微服务中的接口时候,在Zuul层出现异常、超时等,从而导致整…...

C++中的动态内存管理
1.C中动态内存管理 C语言内存管理方式在C中可以继续使用,但有些地方就无能为力,而且使用起来比较麻烦,因此C又提出了自己的内存管理方式:通过new和delete操作符进行动态内存管理。 1.1 new/delete操作内置类型 c语言和c的动态内存…...

es6的核心语法
在学习低代码时,经常有粉丝会问,低代码需要什么基础,es6就是基础中的一项。我们本篇是做一个扫盲,可以让你对基础有一个概要性的了解,具体的每个知识点可以深入进行了解,再结合官方模板就会有一个不错的掌握…...
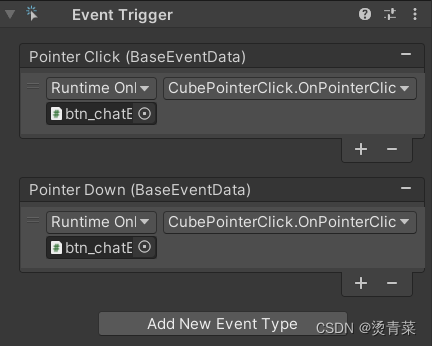
Unity | 射线检测及EventSystem总结
目录 一、知识概述 1.Input.mousePosition 2.Camera.ScreenToWorldPoint 3.Camera.ScreenPointToRay 4.Physics2D.Raycast 二、射线相关 1.3D(包括UI)、射线与ScreenPointToRay 2.3D(包括UI)、射线与ScreenToWorldPoint …...

职业经验 2024 年测试求职手册
原贴地址: 2024 年测试求职手册 TesterHome 经历年前年后差不多 2 个月左右时候的求职,是时候总结复盘一下了,本打算在自己有着落再复盘,但是一想那时候似乎价值就没现在去做显得有意义一些,这篇帖子更多的是让大家看下有没有心…...

Spring Boot与Redis深度整合:实战指南
Spring Boot 整合 Redis 相当简单,它利用了 Spring Data Redis 项目,使得我们可以在 Spring Boot 应用中轻松地操作 Redis。以下是如何整合 Redis 到 Spring Boot 应用的基本步骤: 1. 添加依赖 首先,在你的 pom.xml 文件中添加 …...
微服务(基础篇-006-Docker安装-CentOS7)
目录 05-初识Docker-Docker的安装_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1LQ4y127n4?p46&spm_id_frompageDriver&vd_source60a35a11f813c6dff0b76089e5e138cc 0.安装Docker 1.CentOS安装Docker 1.1.卸载(可选) 1.2.安装dock…...

前端-css-01
1.CSS 长度单位和颜色设置 1.1CSS 中的长度单位 px 像素 em 字体大小的倍数(字体默认是16px) % 百分比 1.2CSS 中的颜色设置方式 1.2.1使用颜色名表示颜色 red、orange、yellow、green、cyan、blue、purple、pink、deeppink、skyblue、greenyellow .…...

Java学习36-Java 多线程安全:懒汉式和饿汉式
JAVA种有两种保证线程安全的方式,分别叫懒汉式Lazy Initialization和饿汉式Eager Initialization,以下是他们的区别: 线程安全性: 懒汉式本身是非线程安全的,因为多个线程可能同时检查实例是否为null,并尝…...

sql常用之CASE WHEN THEN
sql常用之CASE WHEN THEN SQL中的 CASE 类似编程语言里的 if-then-else 语句,用做逻辑判断。可以用于SELECT语句中,也可以用在WHERE,GROUP BY 和 ORDER BY 子句;可以单独使用,也可以和聚合函数结合使用。 语法&#…...
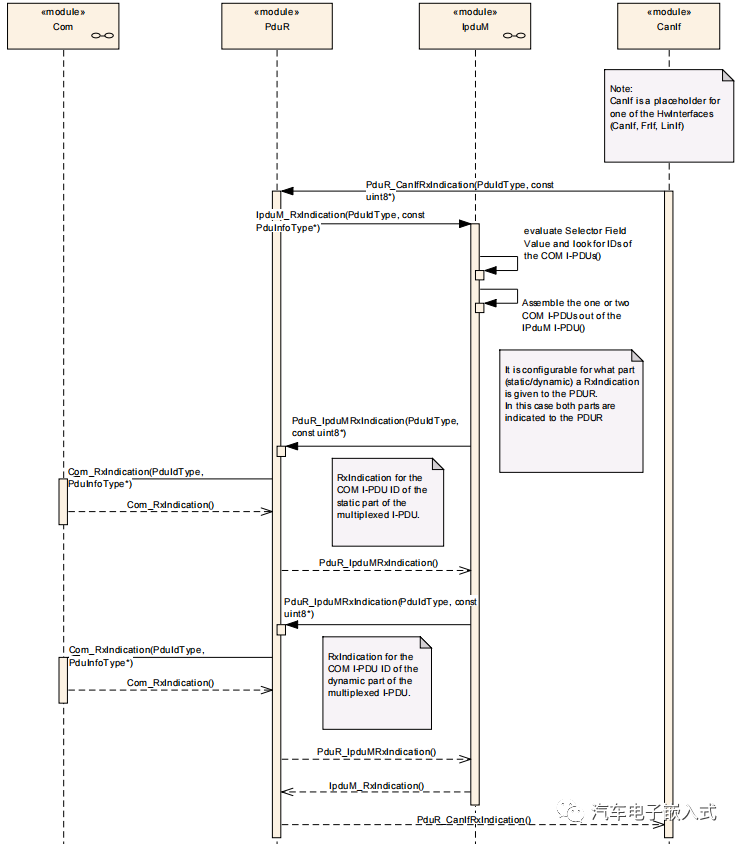
【PduR路由】IPduM模块详细介绍
目录 1.IpduM功能简介 2.IpduM模块依赖的其他模块 2.1RTE (BSW Scheduler) 2.2PDU Router 2.3COM 3.IpduM功能详解 3.1 功能概述 3.2 I-PDU多路复用I-PDU Multiplexing 3.2.1 Definitions and Layout 3.2.2通用功能描述 General 3.2.3模块初始化 Initialization 3.…...
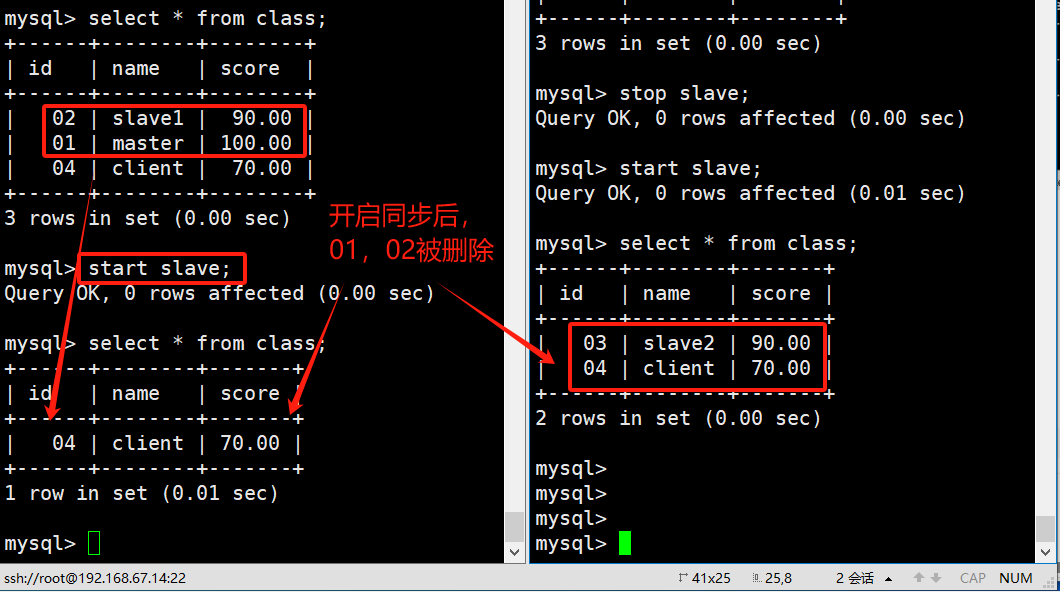
【MySQL】6.MySQL主从复制和读写分离
主从复制 主从复制与读写分离 通常数据库的读/写都在同一个数据库服务器中进行; 但这样在安全性、高可用性和高并发等各个方面无法满足生产环境的实际需求; 因此,通过主从复制的方式同步数据,再通过读写分离提升数据库的并发负载…...

Lucene及概念介绍
Lucene及概念介绍 基础概念倒排索引索引合并分析查询语句的构成 基础概念 Document:我们一次查询或更新的载体,对比于实体类 Field:字段,是key-value格式的数据,对比实体类的字段 Item:一个单词࿰…...

密码算法概论
基本概念 什么是密码学? 简单来说,密码学就是研究编制密码和破译密码的技术科学 例题: 密码学的三个阶段 古代到1949年:具有艺术性的科学1949到1975年:IBM制定了加密标准DES1976至今:1976年开创了公钥密…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
