python实现泊松回归
1 什么是基于计数的数据?
基于计数的数据包含以特定速率发生的事件。发生率可能会随着时间的推移或从一次观察到下一次观察而发生变化。以下是基于计数的数据的一些示例:
- 每小时穿过十字路口的车辆数量
- 每月去看医生的人数
- 每月发现的类地行星数量
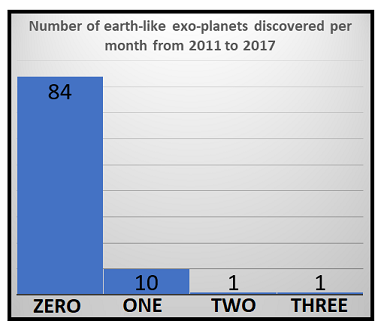
计数数据集具有以下特征:
- 整数数据:数据由非负整数组成:[0… ∞] 。普通最小二乘回归等回归技术可能不适合对此类数据进行建模,因为 OLSR 最适合实数,例如 -656.0、-0.00000345、13786.1 ETC。
- 偏斜分布:数据可能包含少量值的大量数据点,从而使频率分布相当偏斜。请、参见上面的直方图示例。
- 稀疏性:数据可能反映了伽马射线爆发等罕见事件的发生,从而使数据变得稀疏。
- 发生率:为了创建模型,可以假设事件 λ 有一定的发生率来驱动此类数据的生成。事件发生率可能会随着时间的推移而发生变化。
下表包含在纽约市各桥梁上骑行的骑自行车者的计数。从2017年4月1日到2017年10月31日,每天都会测量计数。
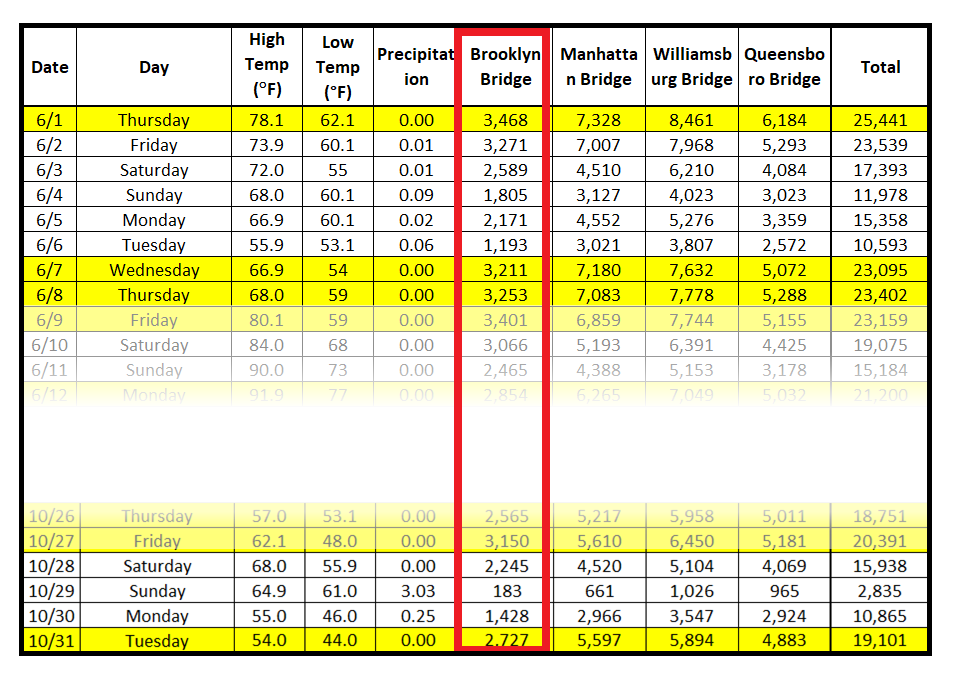
以下是布鲁克林大桥上骑自行车的人计数的时间顺序图:
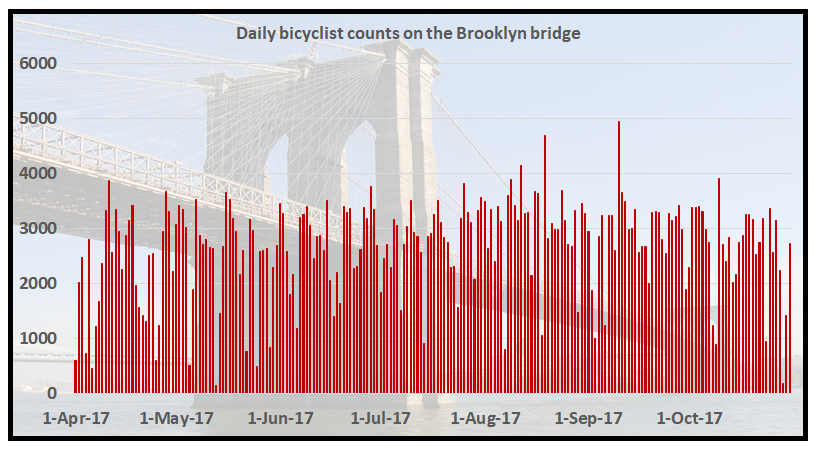
2 计数回归模型
泊松回归模型和负二项式回归模型是开发计数回归模型的两种流行技术。其他可能包括有序 Logit、有序 Probit 和非线性最小二乘模型。
最好从泊松回归模型开始,并将其用作更复杂或约束较少的模型的“控制”。卡梅伦和特里维迪在他们的**《计数数据回归分析》**一书中说道:
“一个合理的做法是估计泊松模型和负二项式模型。”
在本节中,将使用泊松回归模型对布鲁克林大桥上观察到的骑自行车者计数进行回归。
3 泊松模型简介
泊松分布具有以下概率质量函数。
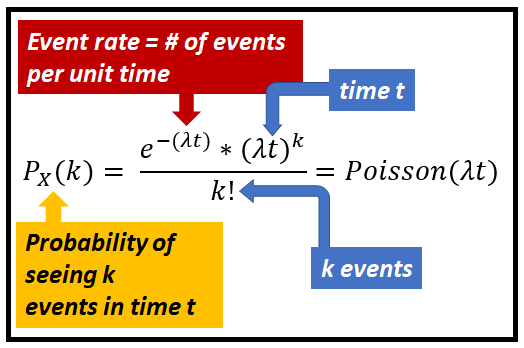
泊松分布的期望值(平均值)是 λ。因此,在缺乏其他信息的情况下,人们应该期望在任何单位时间间隔(例如 1 小时、1 天等)内看到 λ 事件。对于任何时间间隔 t,人们都期望看到 λt 事件。
- 常数 λ 的泊松回归模型
如果事件发生率 λ 是恒定的,则可以简单地使用修改的平均模型来预测未来的事件计数。在这种情况下,可以将所有计数的预测值设置为该恒定值 λ。
下图说明了常数 λ 的场景:

- 非常数 λ 的泊松回归模型
检查一种更常见的情况,其中 λ 可以从一个观察值更改为下一个观察值。在这种情况下,假设 λ 的值受到解释变量向量(也称为预测变量、回归变量或回归变量)的影响,将这个回归变量矩阵称为 X。
回归模型的作用是将观察到的计数 y 拟合到回归值矩阵 X 。
在纽约市骑自行车者计数数据集中,回归变量为日期、星期几、高温、低温和降水量。还可以引入额外的回归量,例如从日期派生的月份和日期,并且可以自由地删除现有的回归量,例如日期:
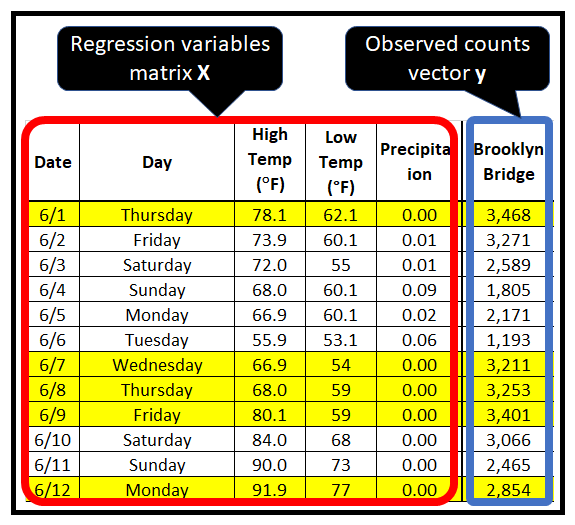
y 与 X 的拟合是通过固定回归系数 β 向量的值来实现的。
在泊松回归模型中,事件计数 y 被假定为泊松分布,这意味着观察 y 的概率是事件率向量 λ 的函数。
泊松回归模型的工作是通过链接函数将观测计数 y 拟合到回归矩阵 X,该链接函数将速率向量 λ 表示为回归系数 β 和 回归矩阵 X 的函数。
下图说明了泊松回归模型的结构。
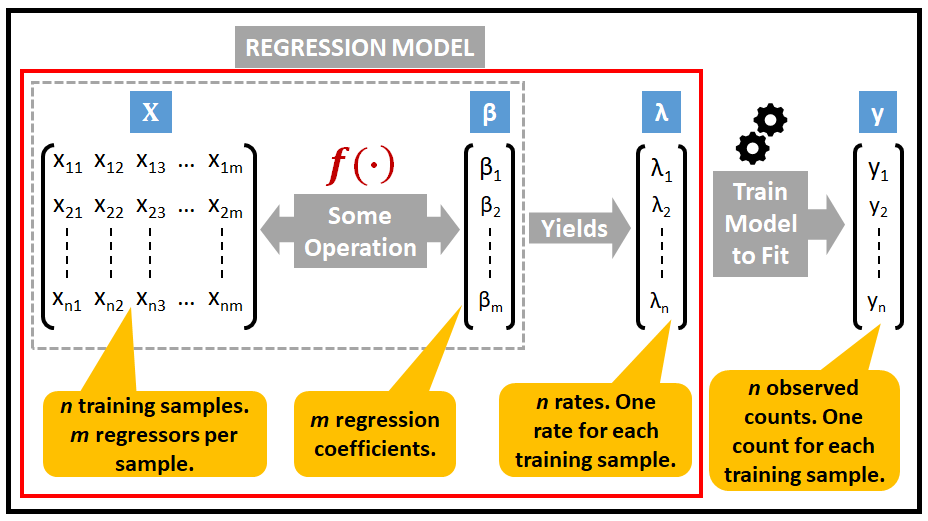
将 λ 与 X 连接起来的良好链接函数 f(.) 是什么?事实证明,以下指数链接函数效果很好:
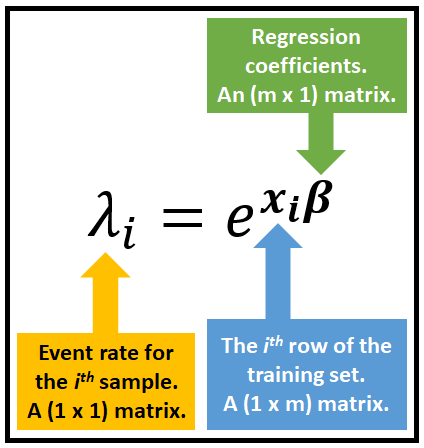
即使当回归量 X 或回归系数 β 具有负值时,该链接函数也使** λ 保持非负值**。这是基于计数的数据的要求。
一般来说,有:

4 泊松回归模型的形式化说明
基于计数的数据的泊松回归模型的完整规范如下:
对于数据集中由 y_i 表示的与回归变量 x_i 行对应的第 i 个观测值,观测计数 y_i 的概率是按照以下 PMF 的泊松分布:

其中第 i 个样本的平均速率 λ_i 由前面所示的指数链接函数给出。在这里重现它:

一旦模型在数据集上得到充分训练,回归系数 β 就已知,模型就可以进行预测了。为了预测与观察到的回归量 x_p 输入行相对应的事件计数 y_p,可以使用以下公式:
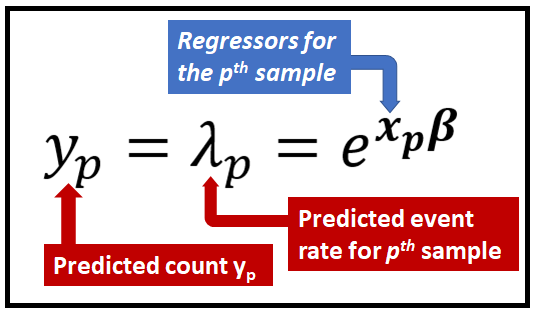
所有这些都取决于成功训练模型的能力,以便已知回归系数向量 β。
接下来看看这个训练是如何进行的。
5 训练泊松回归模型
训练泊松回归模型涉及查找回归系数 β 的值,这将使观察到的计数 y 的向量最有可能。
识别系数 β 的技术称为最大似然估计 (MLE)。
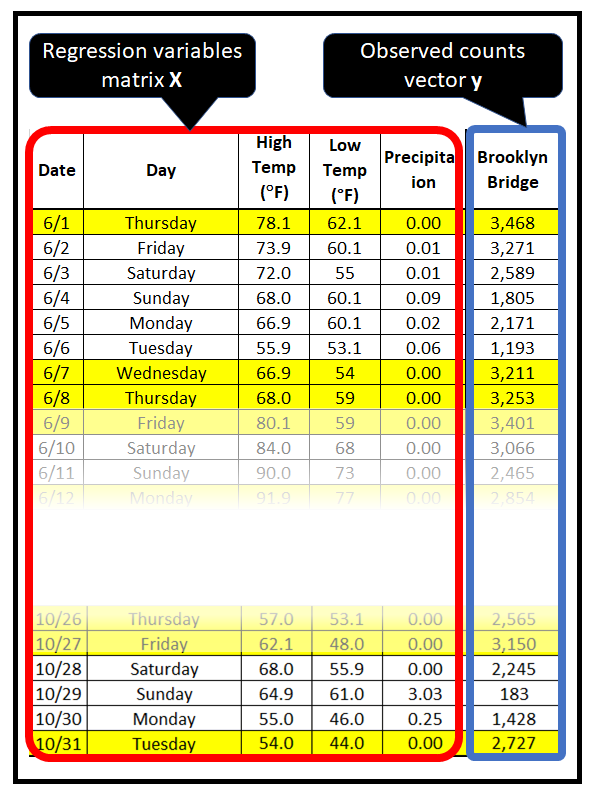
使用骑自行车者计数数据集来说明 MLE 技术。看一下该数据集的前几行:
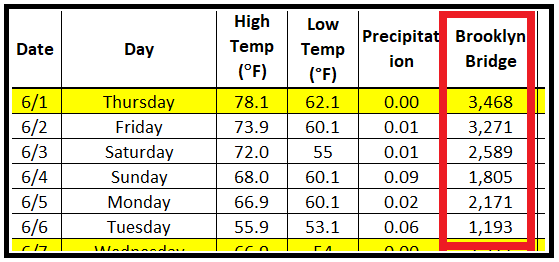
假设红框中显示的骑自行车者计数来自泊松过程。因此可以说它们发生的概率是由泊松 PMF 给出的。以下是前 4 次出现的概率:
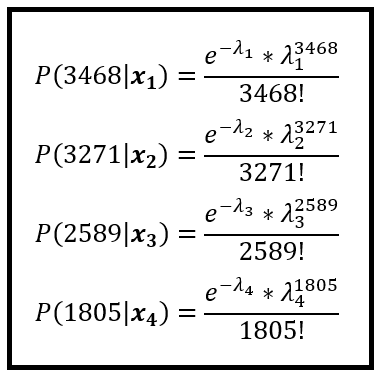
可以类似地计算训练集中观察到的所有 n 个计数的概率。
注意,在上面的公式中,λ_1,λ_2,λ_3,…,λ_n是使用link函数计算的,如下所示:

其中 x_1、x_2、x_3、x_4 是回归矩阵的前 4 行。
训练集中 n 个计数 y_1, y_2,…,y_n 的整个集合出现的概率是各个计数出现的联合概率。
计数 y 服从泊松分布,y_1, y_2,…,y_n 是独立的随机变量,相应地给出 x_1, x_2,…,x_n。因此,y_1、y_2、…、y_n 出现的联合概率可以表示为各个概率的简单乘法。以下是整个训练集的联合概率:
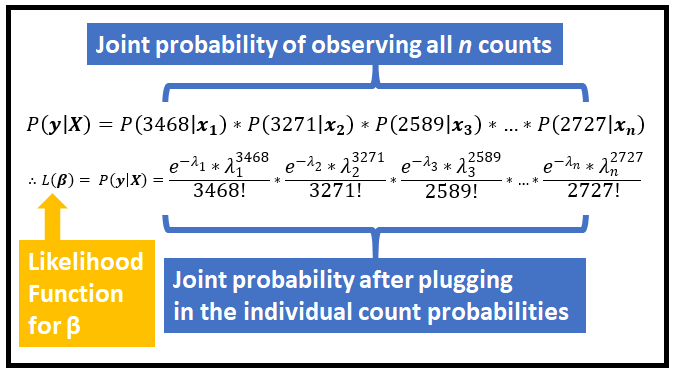
让我们回想一下,λ_1、λ_2、λ_3、…、λ_n 通过回归系数 β 链接到回归向量 x_1、x_2、x_3、…、x_n。
β 的什么值将使给定的观察计数 y 集最有可能出现?它是上式中所示的联合概率达到最大值时的β值。它是 β 的值,其中联合概率函数的对β的变化率为 0。换句话说,它是通过对联合概率方程对 β 进行微分而得到的方程的解并将该微分方程设置为 0。
联合概率方程的对数微分比原方程更容易。对数方程的解产生相同的 β 最优值。
这个对数方程称为对数似然函数。对于泊松回归,对数似然函数由以下等式给出:
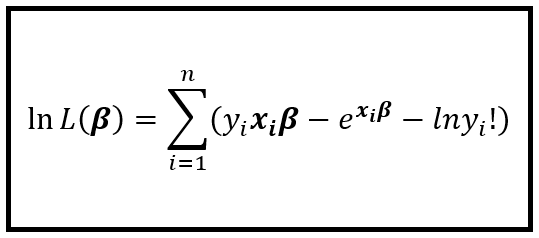
上式是将前面所示的联合概率函数两边取自然对数,并将 λ_i 替换为 exp(x_i*β) 后得到的。
如前所述,对数似然方程对 β 进行微分,并将其设置为零。这个运算提供了以下等式:
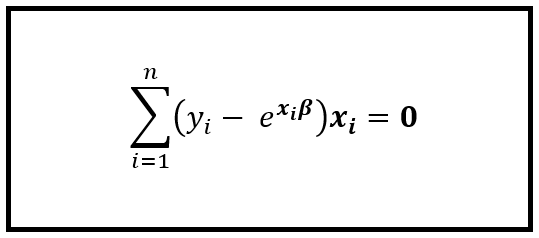
求解回归系数 β 的方程将得到 β 的最大似然估计 (MLE)。
为了求解上述方程,使用迭代方法,例如迭代重加权最小二乘法 (IRLS)。
6 执行泊松回归的步骤摘要
总之,以下是对基于计数的数据集执行泊松回归的步骤:
- 首先,确保数据集包含计数。一种判断方法是它仅包含非负整数值,表示某个时间间隔内某个事件发生的次数。在骑自行车者计数数据集中,它是每天穿过布鲁克林大桥的骑自行车者的数量。
- 找出(或猜测)会影响观察到的计数的回归变量。在骑自行车者计数数据集中,回归变量包括星期几、最低气温、最高气温、降水量等。
- 制定回归模型将用于训练的训练数据集,以及应保留的测试数据集。不要根据测试数据训练模型。
- 使用合适的统计软件(例如 Pythonstatsmodels 包)在训练数据集上配置和拟合泊松回归模型。
- 通过在测试数据集上运行模型来测试模型的性能,以生成预测计数。将它们与测试数据集中的实际计数进行比较。
- 使用拟合优度度量来确定模型在训练数据集上的训练效果。
7 如何在 Python 中训练泊松回归模型
目标是为观察到的骑车人计数 y 建立泊松回归模型。将使用经过训练的模型来预测模型在训练期间未见过的布鲁克林大桥上每日骑自行车的人数。
首先导入所有必需的包。
import pandas as pd
from patsy import dmatrices
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
为计数数据集创建一个 pandas DataFrame。
df = pd.read_csv('nyc_bb_bicyclist_counts.csv', header=0, infer_datetime_format=True, parse_dates=[0], index_col=[0])
我们将向 X 矩阵添加一些导出的回归变量。
ds = df.index.to_series()
df['MONTH'] = ds.dt.month
df['DAY_OF_WEEK'] = ds.dt.dayofweek
df['DAY'] = ds.dt.day
我们不会使用 Date 变量作为回归量,因为它包含绝对日期值,但我们不需要做任何特殊的事情来删除 Date,因为它已经被用作 pandas DataFrame 的索引。所以它在 X 矩阵中对我们来说是不可用的。
让我们创建训练和测试数据集。
mask = np.random.rand(len(df)) < 0.8
df_train = df[mask]
df_test = df[~mask]
print('Training data set length='+str(len(df_train)))
print('Testing data set length='+str(len(df_test)))
以 Patsy 表示法设置回归表达式。BB_COUNT 是因变量,它取决于回归变量:DAY、DAY_OF_WEEK、MONTH、HIGH_T、LOW_T 和 PRECIP。
expr = “”“BB_COUNT ~ DAY + DAY_OF_WEEK + MONTH + HIGH_T + LOW_T + PRECIP”“”
为训练和测试数据集设置 X 和 y 矩阵。 Patsy 让这一切变得非常简单。
y_train, X_train = dmatrices(expr, df_train, return_type='dataframe')
y_test, X_test = dmatrices(expr, df_test, return_type='dataframe')
使用 statsmodels GLM 类,在训练数据集上训练泊松回归模型。
poisson_training_results = sm.GLM(y_train, X_train, family=sm.families.Poisson()).fit()
打印总结。
print(poisson_training_results.summary())
这会打印出以下内容:
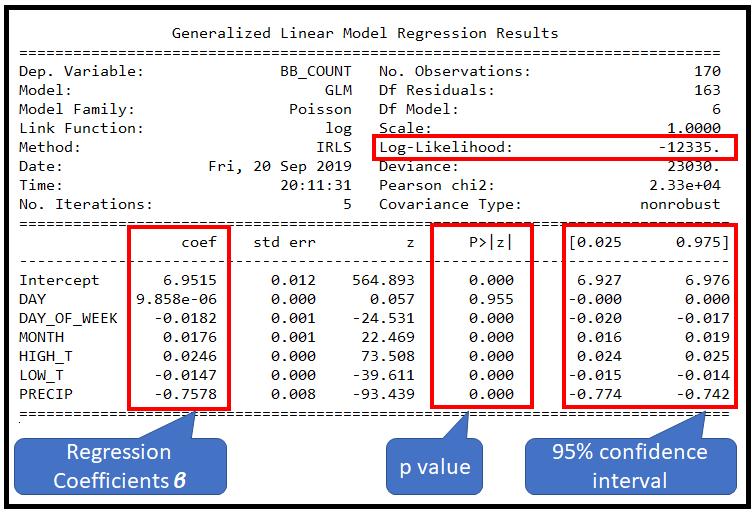
那么模型表现如何?对测试数据集做一些预测。
poisson_predictions = poisson_training_results.get_prediction(X_test)
#summary_frame() returns a pandas DataFrame
predictions_summary_frame = poisson_predictions.summary_frame()
print(predictions_summary_frame)
以下是输出的前几行:

绘制测试数据的预测计数与实际计数。
predicted_counts=predictions_summary_frame['mean']
actual_counts = y_test['BB_COUNT']
fig = plt.figure()
fig.suptitle('Predicted versus actual bicyclist counts on the Brooklyn bridge')
predicted, = plt.plot(X_test.index, predicted_counts, 'go-', label='Predicted counts')
actual, = plt.plot(X_test.index, actual_counts, 'ro-', label='Actual counts')
plt.legend(handles=[predicted, actual])
plt.show()
这是输出:
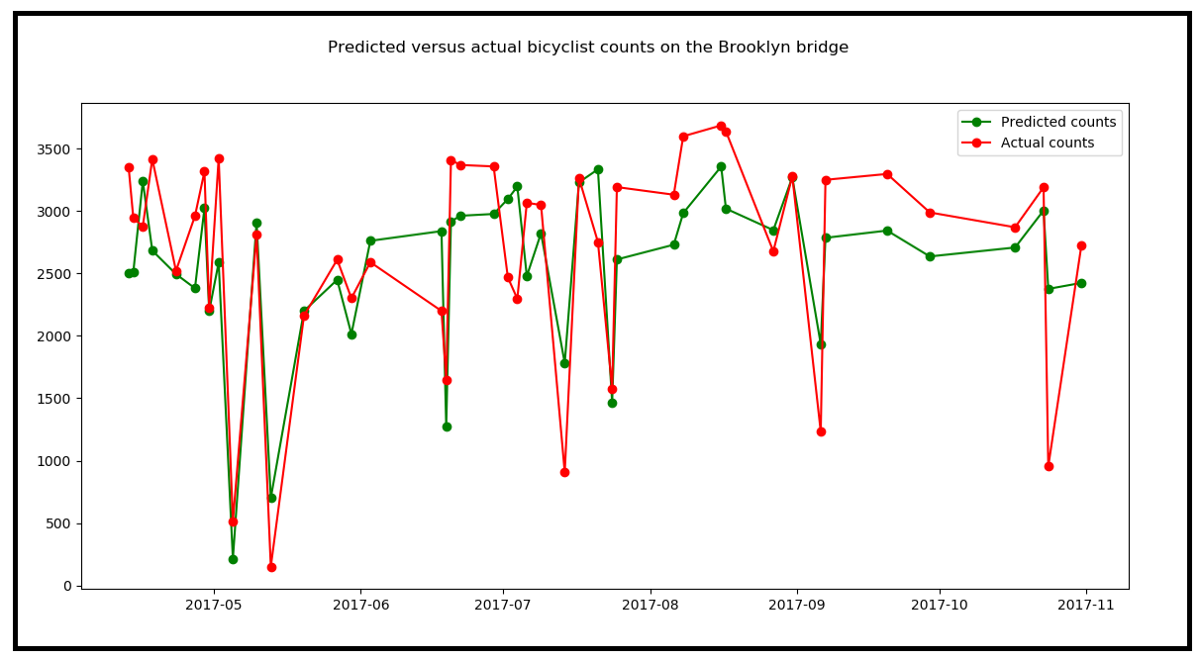
该模型似乎或多或少地跟踪了实际计数的趋势,尽管在许多情况下其预测与实际值相差甚远。
绘制实际计数与预测计数的关系图。
plt.clf()
fig = plt.figure()
fig.suptitle('Scatter plot of Actual versus Predicted counts')
plt.scatter(x=predicted_counts, y=actual_counts, marker='.')
plt.xlabel('Predicted counts')
plt.ylabel('Actual counts')
plt.show()
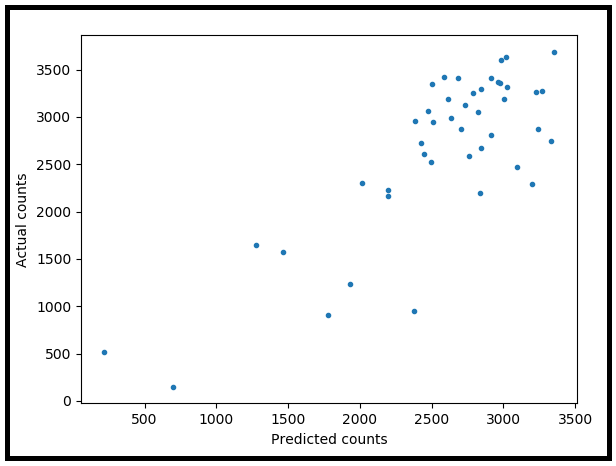
8 泊松回归模型的拟合优度
泊松分布的期望值(即均值)和方差均为 λ。大多数现实世界的数据都违反了这个相当严格的条件。
泊松回归模型失败的一个常见原因是数据不满足泊松分布规定的均值 = 方差标准。
statsmodels GLMResults 类上的 summary() 方法显示了一些有用的拟合优度统计数据,可帮助评估泊松回归模型是否能够成功拟合训练数据。
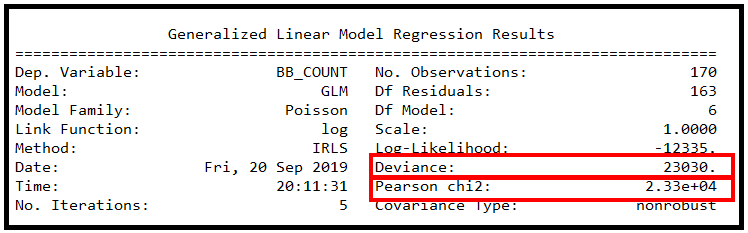
报告的偏差和皮尔逊卡方值非常大。考虑到这些值,几乎不可能实现良好的拟合。为了在某个置信水平(例如 95% (p=0.05))下定量确定拟合优度,在 χ2 表中查找 p=0.05 和残差自由度=163 的值。 (DF 残差 = 观察次数减去 DF 模型])。
将此卡方值与观察到的统计数据进行比较,在本例中为 GLMResults 中报告的偏差或皮尔逊卡方值。在 p=0.05 且 DF 残差 = 163 时,标准卡方表中的卡方值为 193.791,远小于报告的统计数据 23030 和 23300。
因此,根据此测试,泊松回归模型尽管展示了对测试数据集的“良好”视觉拟合,但与训练数据的拟合却相当差。
参考:
https://timeseriesreasoning.com/contents/poisson-regression-model/
https://omarfsosa.github.io/poisson_regression_in_python
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.PoissonRegressor.html
https://mengte.online/archives/12747
相关文章:

python实现泊松回归
1 什么是基于计数的数据? 基于计数的数据包含以特定速率发生的事件。发生率可能会随着时间的推移或从一次观察到下一次观察而发生变化。以下是基于计数的数据的一些示例: 每小时穿过十字路口的车辆数量每月去看医生的人数每月发现的类地行星数量 计数数…...
软件测试-进阶篇
目录 测试的分类1 按测试对象划分1.1 界面测试1.2 可靠性测试1.3 容错性测试1.4 文档测试1.5 兼容性测试1.6 易用性测试1.7 安装卸载测试1.8 安装测试1.9 性能测试1.10 内存泄漏测试 2 按是否查看代码划分2.1 黑盒测试(Black-box Testing)2.2 白盒测试&a…...

Google人才选拔的独特视角
Google人才选拔的独特视角 独特的人才选拔标准 Google作为全球最大的搜索引擎公司,拥有无数优秀的人才。他们的选拔标准与众不同,有着自己独特的人才观。 重视多元化的背景 Google相信人才的多元化背景能够给公司带来不同的思考角度和创新思维。他们…...

OSPF---开放式最短路径优先协议
1. OSPF描述 OSPF协议是一种链路状态协议。每个路由器负责发现、维护与邻居的关系,并将已知的邻居列表和链路费用LSU报文描述,通过可靠的泛洪与自治系统AS内的其他路由器周期性交互,学习到整个自治系统的网络拓扑结构;并通过自治系统边界的路…...
云数据仓库Snowflake论文完整版解读
本文是对于Snowflake论文的一个完整版解读,对于从事大数据数据仓库开发,数据湖开发的读者来说,这是一篇必须要详细了解和阅读的内容,通过全文你会发现整个数据湖设计的起初原因以及从各个维度(架构设计、存算分离、弹性…...

Redis中是如何初始化服务器的?
初始化服务器 一个Redis服务器从启动到能够接受客户端的命令请求,需要经过一系列的初始化和设置过程,比如初始化服务器状态,接受用户指定的服务器配置,创建相应的数据结构和网络连接等等 初始化服务器状态结构 初始化服务器的第…...

深度学习训练过程中,常见的关键参数和概念讲解
深度学习训练过程中的关键参数和概念对于构建、理解和优化模型至关重要。以下是一些最常见的参数和概念,以及它们的简要解释: 1. 学习率(Learning Rate) 学习率是优化算法中最重要的参数之一,它控制着权重调整的幅度…...

如何提高小红书笔记的收录率?
在小红书平台上,笔记的收录率是衡量一篇笔记是否受欢迎和有价值的重要因素。为了提高笔记的收录率,有几个关键点需要注意: 1.内容不涉及广告 在发布笔记前要先确保笔记内容不包含任何形式的广告或推广信息。小红书平台对于广告性质的内容有…...
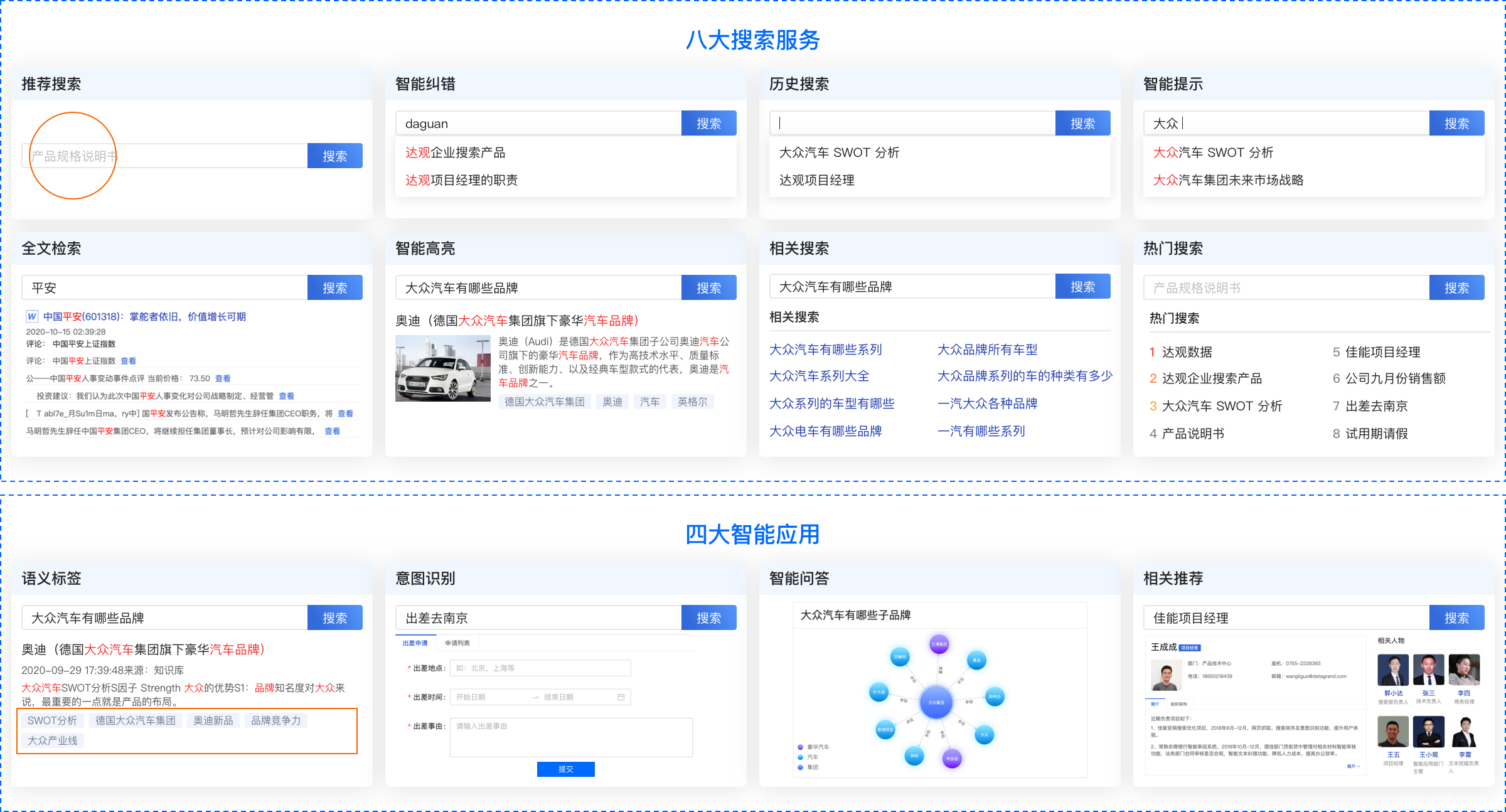
思通数科:利用开源AI能力引擎平台打造企业智能搜索系统
在信息爆炸的时代,如何高效地管理和检索海量数据已成为企业和个人面临的一大挑战。思通数科 StoneDT 多模态AI能力引擎平台,以其强大的自然语言处理(NLP)、OCR识别、图像识别和文本抽取技术,为用户带来了前所未有的智能…...

Nginx配置其实很简单
Nginx配置其实很简单 不管作为前端还是后端,我们工作中或多或少得接触反向代理,比如代理静态页面或者文件、代理接口解决跨域、配置https、配置缓存和负载等等。而这些需求的实现,我们肯定能接触到Nginx,即使我们使用Caddy等等其它代理方式,但也肯定知道Nginx的存在。如果…...
)
Redis中的serverCron函数(一)
serverCron函数 Redis服务器中的serverCron函数默认每隔100毫秒执行一次,这个函数负责管理服务器的资源,并保持服务器自身的良好运转。 更新服务器时间缓存 Redis服务器中有不少功能需要获取系统的当前时间,而每次获取系统的当前时间都需要…...
)
python保存中间变量(学习笔记)
python保存中间变量 原因: 最近在部署dust3r算法,虽然在本地部署了,也能测试出一定的结果,但是发现无法跑很多图片,为了能够测试多张图片跑出来的模型,于是就在打算在autodl上部署算法,但是由…...

CTF wed安全(攻防世界)练习题
一、Training-WWW-Robots 进入网站如图: 翻译:在这个小小的挑战训练中,你将学习Robots exclusion standard。网络爬虫使用robots.txt文件来检查它们是否被允许抓取和索引您的网站或只是其中的一部分。 有时这些文件会暴露目录结构,…...

计算机网络链路层
数据链路 链路是从一个节点到相邻节点之间的物理线路(有线或无线) 数据链路是指把实现协议的软件和硬件加到对应链路上。帧是点对点信道的数据链路层的协议数据单元。 点对点信道 通信的主要步骤: 节点a的数据链路层将网络层交下来的包添…...

VUE3——reactive对比ref
从定义数据角度对比: 。ref用来定义:基本类型数据 。reactive用来定义:对象(或数组)类型数据。 。备注:ref也可以用来定义对象(或数组)类型数据,它内部会自动通过 reactive 转为代理对象。 从原理角度对比: 。ref通过 object.defineProperty()的 get 与set 来实现响应式(数据劫…...

广场舞团系统的设计与实现|Springboot+ Mysql+Java+ B/S结构(可运行源码+数据库+设计文档)
本项目包含可运行源码数据库LW,文末可获取本项目的所有资料。 推荐阅读100套最新项目持续更新中..... 2024年计算机毕业论文(设计)学生选题参考合集推荐收藏(包含Springboot、jsp、ssmvue等技术项目合集) 目录 1. 系…...
经典永不过时 Wordpress模板主题
经得住时间考验的模板,才是经典模板,带得来客户的网站,才叫NB网站。 https://www.jianzhanpress.com/?p2484...
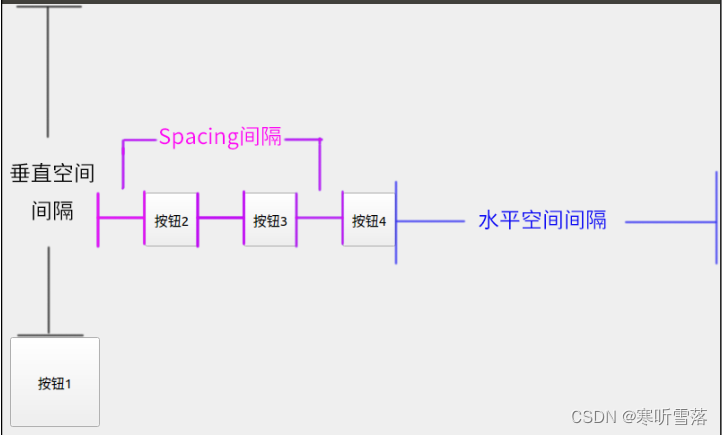
QT布局管理和空间提升为和空间间隔
QHBoxLayout:按照水平方向从左到右布局; QVBoxLayout:按照竖直方向从上到下布局; QGridLayout:在一个网格中进行布局,类似于HTML的table; 基本布局管理类包括:QBoxLayout、QGridL…...
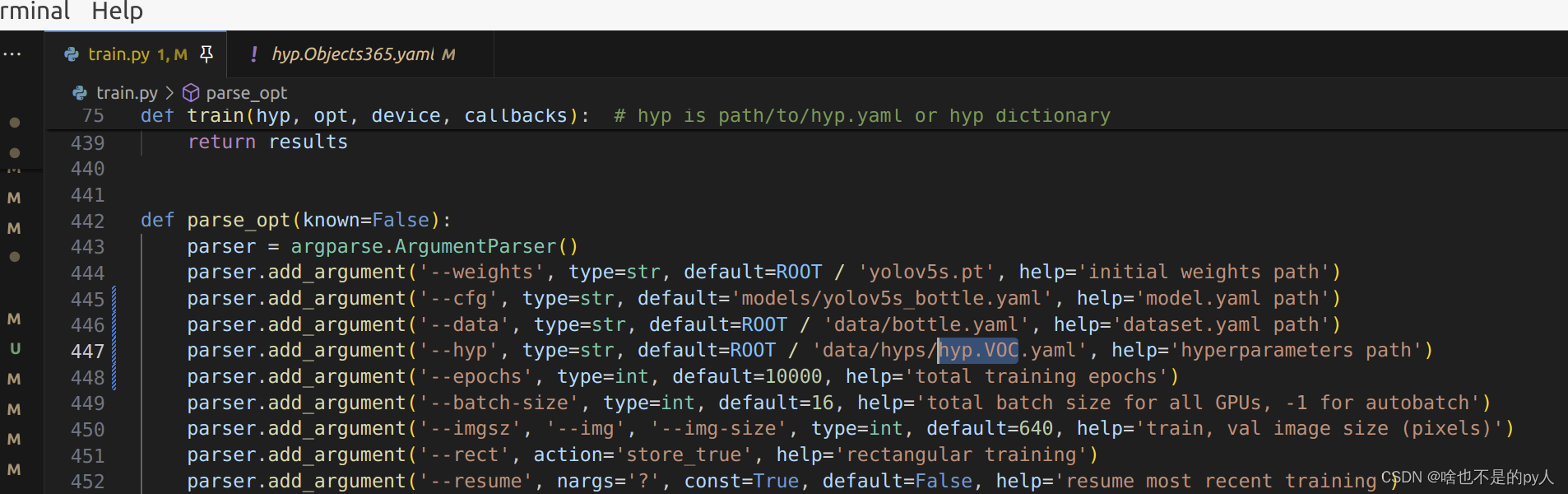
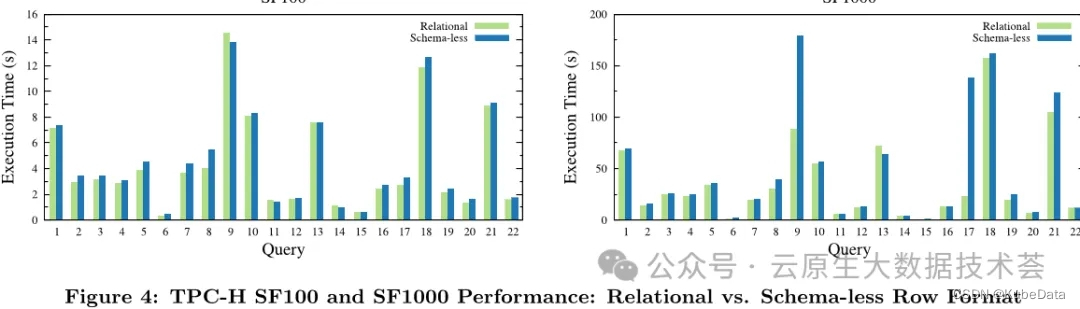
Yolo 自制数据集dect训练改进
上一文请看 Yolo自制detect训练-CSDN博客 简介 如下图: 首先看一下每个图的含义 loss loss分为cls_loss, box_loss, obj_loss三部分。 cls_loss用于监督类别分类,计算锚框与对应的标定分类是否正确。 box_loss用于监督检测框的回归,预测框…...

vlan间单臂路由
【项目实践4】 --vlan间单臂路由 一、实验背景 实验的目的是在一个有限的网络环境中实现VLAN间的通信。网络环境包括两个交换机和一个路由器,交换机之间通过Trunk链路相连,路由器则连接到这两个交换机的Trunk端口上。 二、案例分析 在网络工程中&#…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
