matlab中旋转矩阵函数
文章目录
- matlab里的旋转矩阵、四元数、欧拉角
- 四元数
- 根据两向量计算向量之间的旋转矩阵和四元数
- 欧拉角转旋转矩阵
- 旋转矩阵转欧拉角
- 旋转矩阵转四元数
- 参考链接
matlab里的旋转矩阵、四元数、欧拉角
| 旋转矩阵 | dcm | R |
|---|---|---|
| 四元数 | quat | q=[q0,q1,q2,q3] |
| 欧拉角 | angle | [row,pitch,yaw] |
% 旋转矩阵转四元数
q = dcm2quat(R)
% 欧拉角转四元数
q = angle2quat(r1,r2,r3,S)
% 旋转矩阵转欧拉角
[r1,r2,r3] = dcm2angle(R,S)
% 四元数转欧拉角
[r1,r2,r3] = quat2angle([q0 q1 q2 q3],S)
% S是['ZYX','ZYZ’,‘ZXY’,‘ZXZ’,‘YXZ’,‘YXY’,‘YZX’,‘YZY’,‘XYZ’,‘XYX’,‘XZY’,‘XZX’]
% 四元数转旋转矩阵
R = quat2dcm([q0 q1 q2 q3])
% 欧拉角转旋转矩阵
R = angle2dcm(r1,r2,r3,S)
四元数
% 四元数单元化
q1=quatnormalize(q1);
% 四元数转为旋转矩阵,q1是单元化四元数
R1=quat2dcm(q1);%q1的第一位是实部
% 模(Modulus)
quatmod(p)
% 范数(Norm)
quatnorm(p)
% 单位化(Normalize)
quatnormalize(p)
% 求逆(Inverse)
quatinv(p)
% 四元数除法
quatdivide(q,p)
% 四元数乘法
quatmultiply(p,q)
% 共轭四元数
quatconj(p)
% 旋转函数
quatrotate(p)
% 四元数和欧拉角互换的函数
quat2angle(p)
angle2quat(p)
根据两向量计算向量之间的旋转矩阵和四元数
function [R, q, theta] = vec2quat_R(v1, v2)% 将向量转换为单位向量u1 = v1/norm(v1);u2 = v2/norm(v2);if norm(u1+u2) == 0q = [0 0 0 0];elseu = cross(u1,u2);u = u/norm(u);theta = acos(dot(u1,u2));q = [cos(theta/2) sin(theta/2)*u];end% 四元数转为方向余弦矩阵dcm=[2*q(1).^2-1+2*q(2)^2 2*(q(2)*q(3)+q(1)*q(4)) 2*(q(2)*q(4)-q(1)*q(3));2*(q(2)*q(3)-q(1)*q(4)) 2*q(1)^2-1+2*q(3)^2 2*(q(3)*q(4)+q(1)*q(2));2*(q(2)*q(4)+q(1)*q(3)) 2*(q(3)*q(4)-q(1)*q(2)) 2*q(1)^2-1+2*q(4)^2];% 四元数转为旋转矩阵rot = permute(dcm, [2 1 3]);
end
欧拉角转旋转矩阵
function R = Eular2R(x,y,z,mode)Rotx = [1 0 0;0 cos(x) -sin(x);0 sin(x) cos(x)];Roty = [cos(y) 0 sin(y);0 1 0;-sin(y) 0 cos(y)];Rotz = [cos(z) -sin(z) 0;sin(z) cos(z) 0;0 0 1];switch modecase 1 %ZYXR = Rotz*Roty*Rotx;case 1 %XYZR = Rotx*Roty*Rotz;case 1 %ZXYR = Rotz*Rotx*Roty;case 1 %YZXR = Roty*Rotz*Rotx;otherwiseR = Rotz*Roty*Rotx;end
旋转矩阵转欧拉角
function eular = R2eular(R)x = atan2(R(3,2),R(3,3));y = atan2(-R(3,1),sqrt(R(3,2)^2+R(3,3)^2));z = atan2(R(2,1),R(1,1));eular = [x y z];
旋转矩阵转四元数

function q = R2quat(R)t=sqrt(1+R(1,1)+R(2,2)+R(3,3))/2;q=[t (R(3,2)-R(2,3))/(4*t) (R(1,3)-R(3,1))/(4*t) (R(2,1)-R(1,2))/(4*t)];
end
参考链接
Matlab ——旋转矩阵,四元数,欧拉角之间的转换
相关文章:

matlab中旋转矩阵函数
文章目录 matlab里的旋转矩阵、四元数、欧拉角四元数根据两向量计算向量之间的旋转矩阵和四元数欧拉角转旋转矩阵旋转矩阵转欧拉角旋转矩阵转四元数参考链接 matlab里的旋转矩阵、四元数、欧拉角 旋转矩阵dcmR四元数quatq[q0,q1,q2,q3]欧拉角angle[row,pitch,yaw] % 旋转矩阵…...

探讨Spring Boot的自动配置原理
Spring Boot以其简化Spring应用开发和部署的能力而广受欢迎。其中最引人注目的特性之一就是自动配置,它极大地减少了开发者需要手动编写的配置量。在本篇博客中,我们将深入探讨Spring Boot自动配置的工作原理,以及它是如何使得Spring应用的配…...

【LeetCode】热题100 刷题笔记
文章目录 T1 两数之和T49 字母异位词分组常用小技巧 T1 两数之和 链接:1. 两数之和 题目: 【刷题感悟】这道题用两层for循环也能做出来,但我们还是要挑战一下时间复杂度小于 O ( n 2 ) O(n^2) O(n2)的解法,不能因为它是第一道 …...
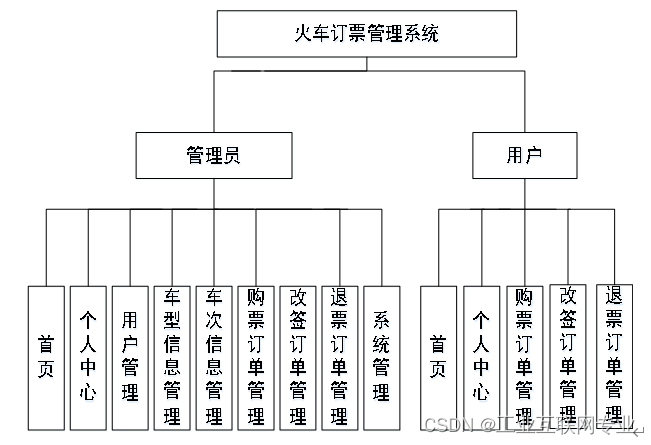
基于springboot+vue+Mysql的火车订票管理系统
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
C#学习笔记 面试提要
冒泡 for (int m 0; m < arr.Length; m) { for (int n 0; n < arr.Length - 1 - m; n) { if (arr[n] > arr[n1]) { int temp arr[n]; arr[n] arr[n 1]; arr[n1] temp; } } } 选择 for (int m 0; m < arr.Length; m) { int index 0; for (int n 1; n < …...

Linux用户识别与身份验证命令一览
这些命令在系统管理、用户管理和监控工作中扮演着重要的角色。下面,介绍它们的类型及功能描述: 一、系统信息命令 hostname:此命令用于显示系统的主机名,它代表了系统在网络中的唯一标识。hostname -f:此命令进一步展…...
)
【Linux】GCC编译器(七)
文章目录 初步了解安装 GCC编译第一个程序编译选项 初步了解 GCC是GNU Compiler Collection的缩写,是一个由GNU项目开发的编译器集合。 GCC的历史和发展:GCC最初由理查德斯托曼(Richard Stallman)发起,目的是创建一个…...
【目录整理】(五)
Git 基础 Git 详细安装教程文章浏览阅读10w次,点赞9.6k次,收藏1.7w次。Git 是个免费的开源分布式版本控制系统,下载地址为git-scm.com 或者 gitforwindows.org,本文介绍 Git-2.40.0-64-bit.exe 版本的安装方法&#x…...

项目:USB键盘和鼠标的复合设备
我们的复合设备使用一个物理设备就可以完成多个功能。 使用复合设备同时完成USB键盘和鼠标功能,它的主要实现方式有两种, 第一个就是我们将多个设备描述符合并成一个,这个相对比较简单,我们只要根据相应的报告描述符处理数据就可…...
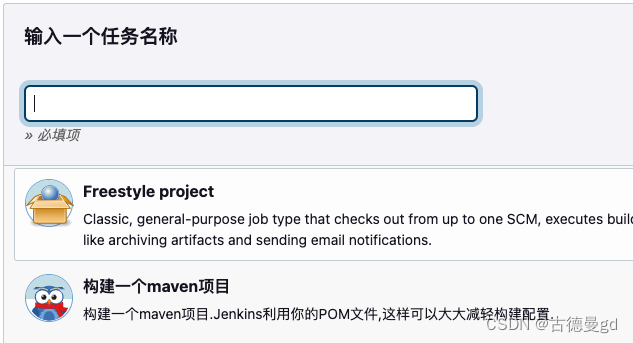
Linux利用Jenkins部署SpringBoot项目保姆级教程
在当今快速发展的软件开发领域,持续集成和持续部署(CI/CD)已经成为提升开发效率、缩短产品上市时间的关键实践。Linux系统以其稳定性和开源友好性,成为众多开发者和企业的首选平台。而Spring Boot,作为一个轻量级的Jav…...

elementUI 输入框按回车刷新页面问题
分析原因: 当 el-form 表单内只有一个 el-input 输入框时,且type为text类型时,在输入框内按回车就会触发表单的提交事件。 而当 el-form 表单内有多个 el-input 输入框时,按回车不会执行任何操作。 使用.prevent修饰符来阻止默…...

C++的字节对齐
什么是字节对齐 参考什么是字节对齐,为什么要对齐? 现代计算机中,内存空间按照字节划分,理论上可以从任何起始地址访问任意类型的变量。但实际中在访问特定类型变量时经常在特定的内存地址访问,这就需要各种类型数据按照一定的规…...
ALPHA开发板上的PHY芯片驱动:LAN8720驱动
一. 简介 前面文章了解到,Linux内核是有提供 PHY通用驱动的。 本文来简单了解一下ALPHA开发板上的 PHY网络芯片LAN8720的驱动。是 LAN8720芯片的公司提供的 PHY驱动。 二. ALPHA开发板上的PHY芯片驱动:LAN8720驱动 我 们 来 看 一 下 LAN8720A 的 …...
:球球大作战)
C语言游戏实战(9):球球大作战
前言: 这款简易版的球球大作战是一款单人游戏,玩家需要控制一个小球在地图上移动,吞噬其他小球来增大自己的体积。本游戏使用C语言和easyx图形库编写,旨在帮助初学者了解游戏开发的基本概念和技巧。 在开始编写代码之前…...
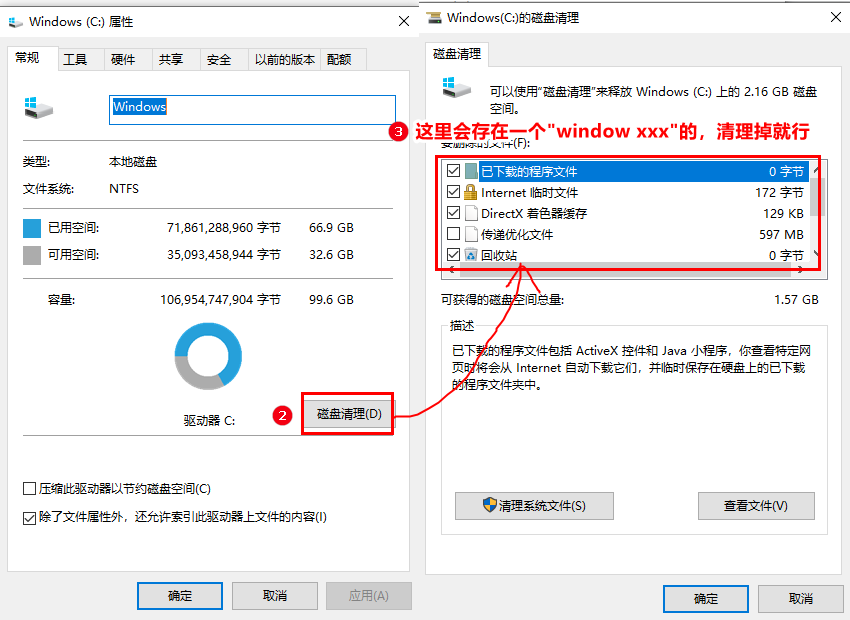
【Windows】关闭自动更新
右键单击“此电脑”,点击“管理”。 找到:任务计划程序 -> 任务计划程序库 -> Microsoft -> Windows -> WindowsUpdate 右键单击Scheduled Start任务,然后点击“禁用”即可。 可能还会存在左下角提示更新重启的字样&#x…...
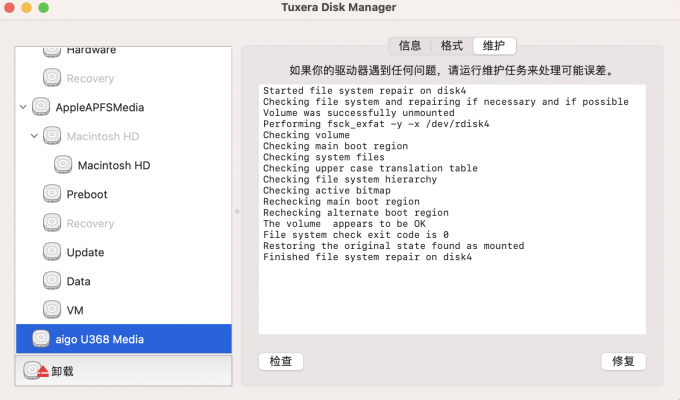
mac如何检测移动硬盘 mac硬盘检测工具 Tuxera怎么用 Tuxera NTFS官网
在工作学习中,我们都绕不开用移动硬盘来拷贝存储一些文件。但是在使用过程中,我们经常遇到“mac检测不到移动硬盘”“移动硬盘不存在”等问题,今天本文就带大家了解下mac如何检测移动硬盘,mac硬盘检测工具。 一、mac如何检测移动…...
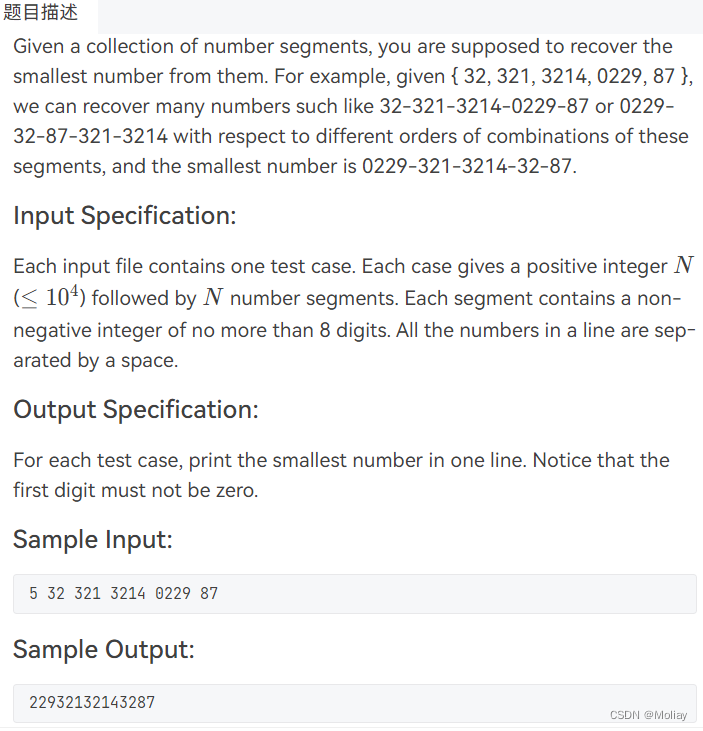
1038 Recover the Smallest Number
idea 给出若干个可能含有前导0的数字串,将其进行拼接使其组成的数最小。 拼接串,想到借助string。 找最小,样例中的32,321, 3214尤为具备代表性,让字典序小的数尽可能靠前,联想到string的比较规则也是字典序 >判断…...

【Go】四、包名、访问范围控制、标识符、运算符
文章目录 1、_2、包名3、命名大小影响可访问范围4、运算符5、获取终端输入 1、_ 下划线"_"本身在Go中是一个特殊的标识符,称为空标识符用于忽略某个值 1)忽略导入的没使用的包 2)忽略某个返回值 2、包名 main包是程序的入口包&a…...

达梦数据库日志文件管理
达梦数据库日志文件管理 联机重做日志管理归档日志文件管理开启归档模式:SQL开启归档模式:dmarch.ini归档文件切换和删除 联机重做日志管理 检查联机重做日志: select * from v$rlog; --CUR_FILE表示正在使用的日志文件编号select * fr…...

zookeeper 监控 与 JVM 设置
一、通过JMX监控 JVM 默认情况下,在 ./bin/zkServer.sh 脚本中是默认开启了JMX监控的,并且是不需要认证的,详情可见ZOOMAIN变量; ZOOMAIN"-Dcom.sun.management.jmxremote -Dcom.sun.management.jmxremote.port$JMXPORT -D…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...
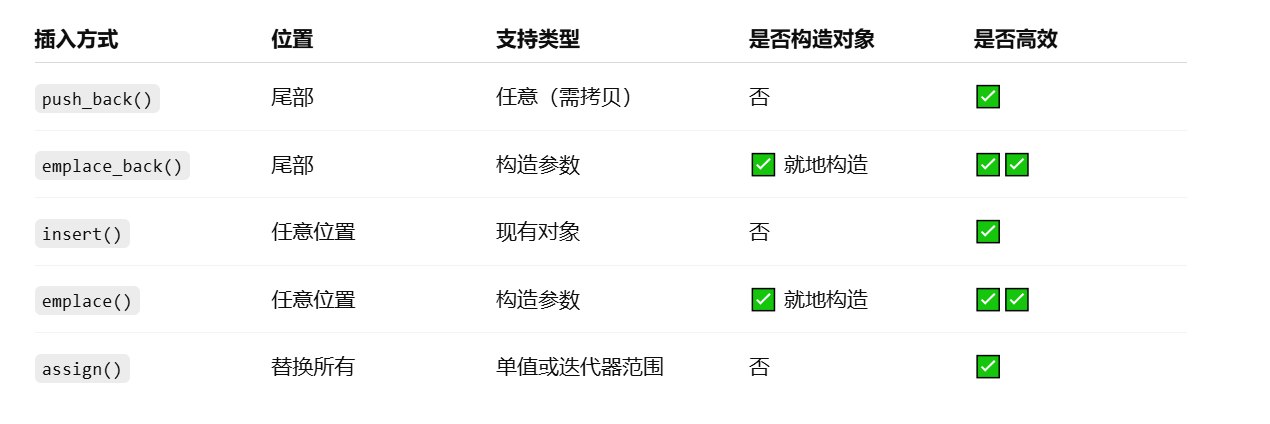
C++中vector类型的介绍和使用
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...
