回收站删除的文件在哪里?专业恢复方法分享(最新版)
“我很想知道我从回收站删除的文件被保存在哪里了呢?我刚刚不小心清空了回收站,现在想将它们恢复,应该怎么操作呢?谁能教教我怎么从回收站恢复文件?”
回收站,作为Windows操作系统中的一个重要组件,承担着临时存储已删除文件的任务。但有时候,由于各种原因,我们可能需要找回那些已被删除的文件。
那么,回收站删除的文件究竟去了哪里?又该如何找回它们呢?本文将详细解答回收站删除的文件在哪里,并给大家分享几个好用的恢复方法。

回收站删除的文件存储位置
很多用户可能都很好奇,当我们清空回收站后,回收站删除的文件在哪里呢?其实,作为一个特殊的文件夹,它通常存储在C盘中,但处于隐藏状态。
如果我们想恢复回收站删除的文件,可以尝试使用下方的方法,这些方法操作起来都比较简单,相信会对大家有所帮助!

方法一:快捷键恢复回收站文件
很多用户可能会在文件删除后就意识误删了重要的数据,不小心把回收站清空了怎么恢复?此时建议大家先借助快捷键来对数据进行恢复,这是比较有效率的方法。
步骤1:当我们进行完删除操作后,不要继续操作;
步骤2:在空白处按下快捷键【Ctrl+Z】撤销上一步的删除操作;
步骤3:如果界面没反应,可尝试重复操作几次步骤2。
提示:该方法使用比较局限,如果按下快捷键一直没有反应,建议尝试其他方法。

方法二:备份恢复回收站文件
怎样找回电脑回收站清空的文件?对于很多用户来说,备份文件已经成了一种必备的习惯。如果我们清空的回收站文件有备份,那么通过备份有机会更有效率的恢复回收站文件。可以这样操作。
步骤1:查看所需文件是否有备份;
步骤2:确认文件有备份后,检查文件的完整性,将它重新复制或下载到电脑空间充足的磁盘。

方法三:专业软件恢复回收站文件
对于很多电脑小白来说,动手操作可能不是一件很简单的事,那么,我们还能怎样找回电脑回收站已清空的文件呢?可以试试 数 据 蛙 恢 复 专 家 。这款软件是支持多种存储设备的数据恢复的,同时,软件还有简单的操作界面,对电脑用户是很友好的。
并且软件支持一键安全快速扫描,有利于帮助大家减少操作失误。软件还支持免费试用,有需要使用软件的用户可以先下载软件,并按下文方法操作。
操作环境:
演示机型:神舟战神G9-CU7PK
系统版本:Windows10
软件版本:数 据 蛙 恢 复 专 家3.3.10
步骤1:将软件下载后可以运行它,新用户点击【免费试用】可获得免费扫描机会;
步骤2:在选择界面,将想要恢复的文件类型勾选上,并将【回收站】勾选上,单击【扫描】;

步骤3:等待扫描完成,用户可以对扫描到的数据进行查看,在查看时,如果文件比较多,可以直接借助【筛选器】,搜索需要恢复的文件,定位到后,将它勾选上;

步骤4:勾选上所有需要恢复的文件后,点击【导出】,并将导出后的数据保存到与文件原保存位置有所区别的位置上。

回收站作为一个重要的工具,给我们带来了很多的便利。回收站删除的文件在哪里?相信看完上文大家应该已经知道了吧!需要恢复回收站文件的用户快快尝试吧!在操作过程中,我们也需要注意保护数据安全,避免对磁盘造成进一步损害。同时,定期备份重要文件也是一个良好的习惯,可以在文件丢失时快速恢复哦。
往期推荐:
硬盘数据恢复工具分享,这4个实用工具要记好!![]() https://blog.csdn.net/datarecover/article/details/137219519?spm=1001.2014.3001.5501
https://blog.csdn.net/datarecover/article/details/137219519?spm=1001.2014.3001.5501
回收站文件恢复,这3个专业方法你值得拥有!![]() https://blog.csdn.net/datarecover/article/details/137223569?spm=1001.2014.3001.5501
https://blog.csdn.net/datarecover/article/details/137223569?spm=1001.2014.3001.5501
电脑搜索功能不能用了?4个宝藏解决方法大公开!![]() https://blog.csdn.net/datarecover/article/details/137222278?spm=1001.2014.3001.5501
https://blog.csdn.net/datarecover/article/details/137222278?spm=1001.2014.3001.5501
相关文章:
回收站删除的文件在哪里?专业恢复方法分享(最新版)
“我很想知道我从回收站删除的文件被保存在哪里了呢?我刚刚不小心清空了回收站,现在想将它们恢复,应该怎么操作呢?谁能教教我怎么从回收站恢复文件?” 回收站,作为Windows操作系统中的一个重要组件…...

什么是工时管理软件?
简而言之,工时管理软件是一种可以帮助管理者跟踪企业员工在项目和任务上花费的时间的软件。然而,工时管理软件不仅是一种收集信息的工具,它还是一种解决方案,使企业能够处理和优化不同的流程和活动,例如工资单、项目预…...
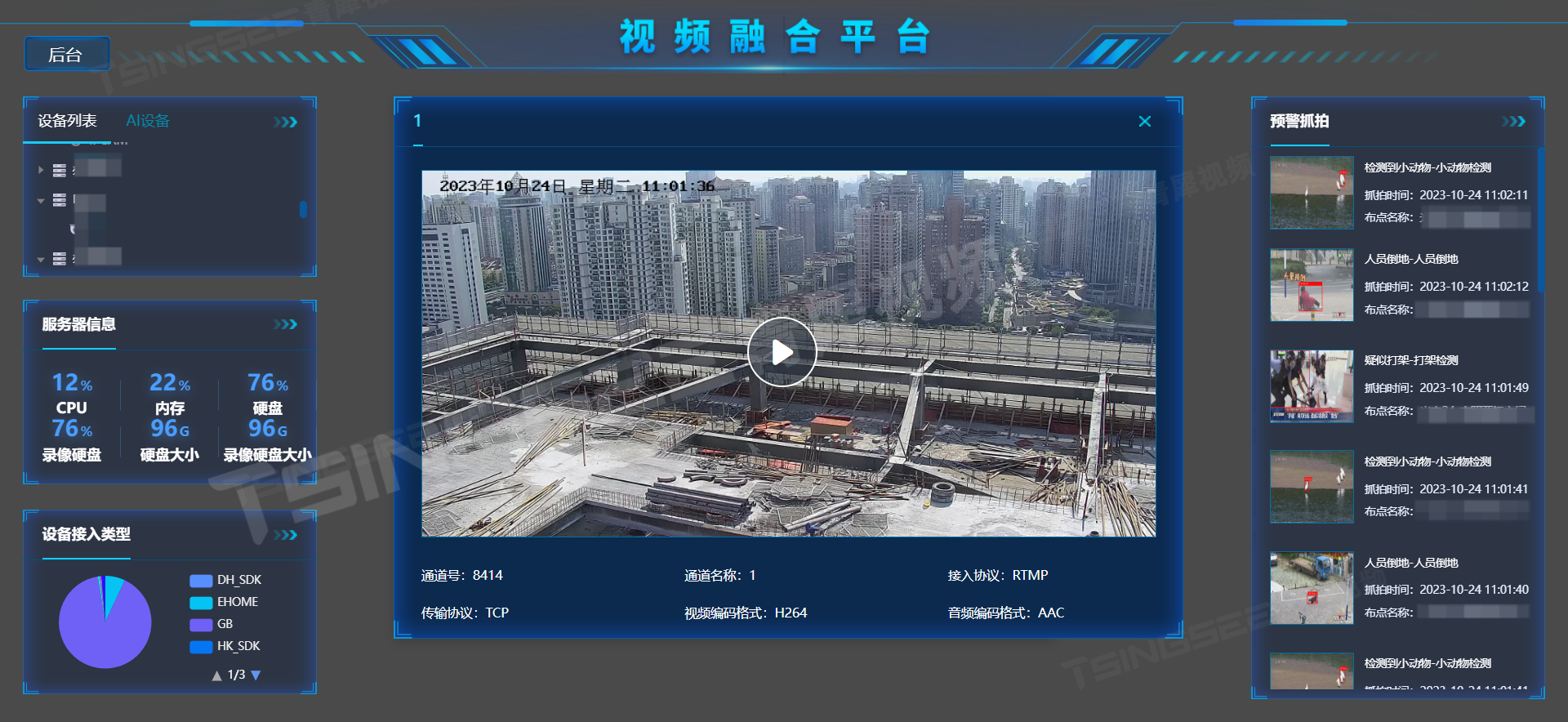
一文解析智慧城市,人工智能技术将成“智”理主要手段
长期以来,有关智慧城市的讨论主要围绕在技术进步方面,如自动化、人工智能、数据的公开以及将更多的传感器嵌入城市以使其更加智能化。实际上,智慧城市是一个关于未来的设想,其重要原因在于城市中存在各种基础设施、政治、地理、财…...
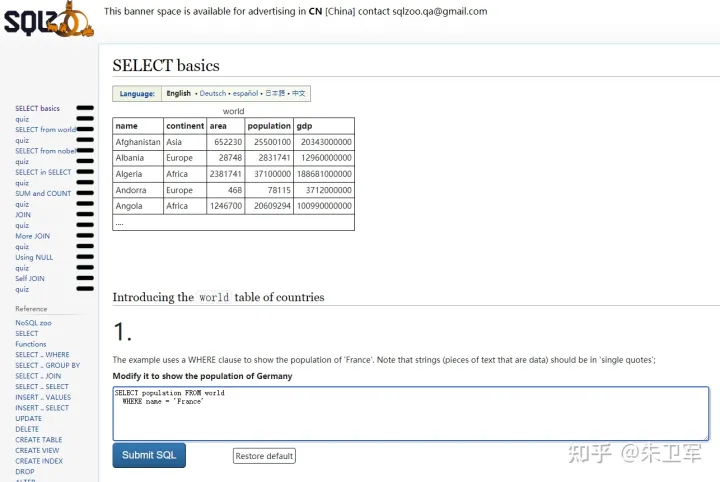
SQLBolt,一个练习SQL的宝藏网站
知乎上有人问学SQL有什么好的网站,这可太多了。 我之前学习SQL买了本SQL学习指南,把语法从头到尾看了个遍,但仅仅是心里有数的程度,后来进公司大量的写代码跑数,才算真真摸透了SQL,知道怎么调优才能最大化…...

TikTok防关联引流系统:全球多账号运营的终极解决方案
tiktok防关联引流系统介绍,tiktok防关联系统是基于tiktok生态研发的效率工具,帮你快速实现tiktok全球多账号运营,系统配备了性能强劲的安卓,防关联智能终端,可一建创建全球多国手机环境,完美满足各类app软件…...
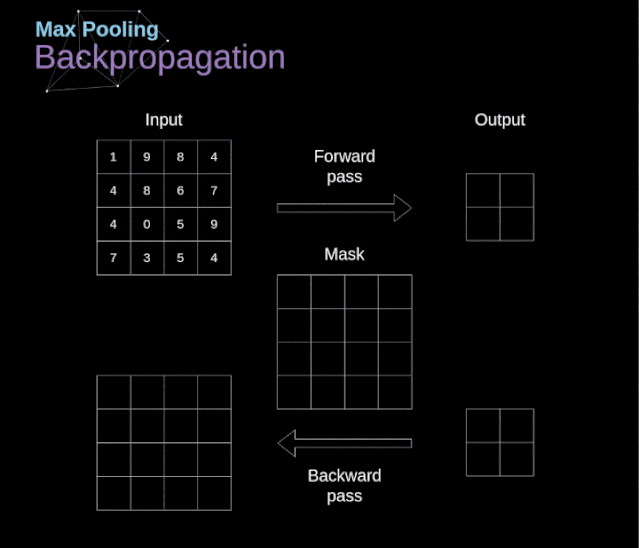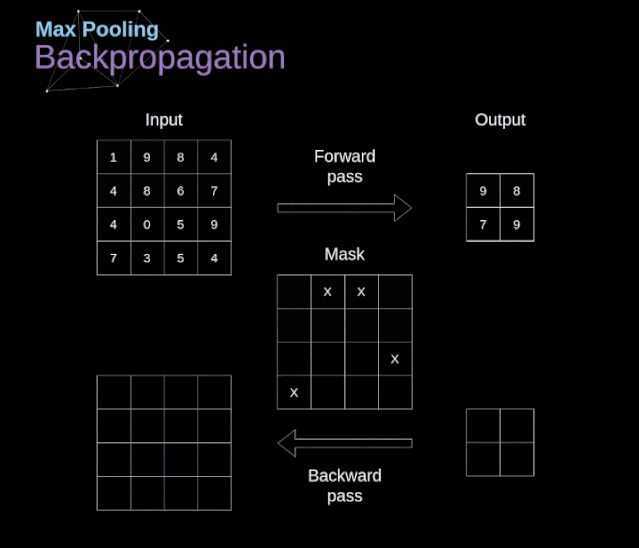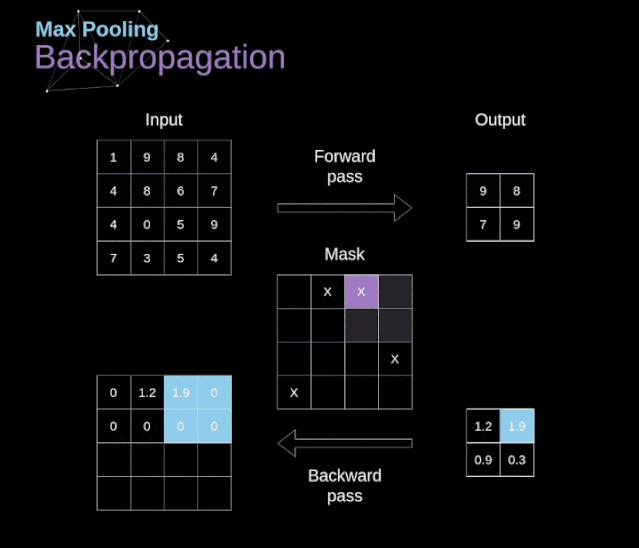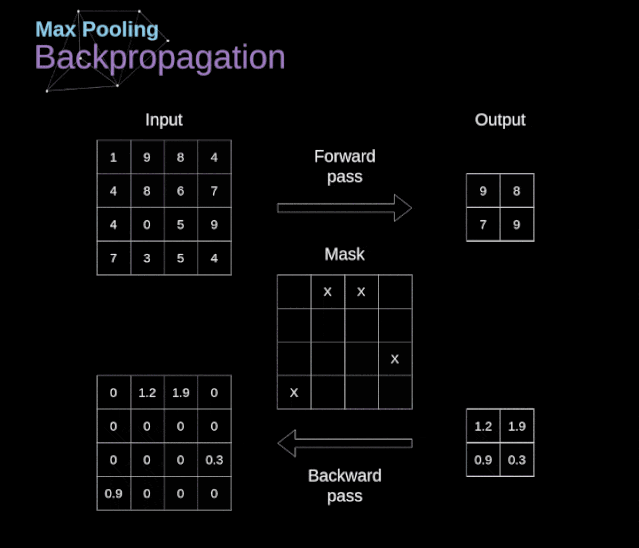
卷积神经网络(CNN)的数学原理解析
文章目录 前言 1、介绍 2、数字图像的数据结构 3、卷积 4、Valid 和 Same 卷积 5、步幅卷积 6、过渡到三维 7、卷积层 8、连接剪枝和参数共享 9、卷积反向传播 10、池化层 11、池化层反向传播 前言 本篇主要分享卷积神经网络(CNN)的数学原理解析…...
)
2024年华为OD机试真题-亲子游戏-Java-OD统一考试(C卷)
题目描述: 宝宝和妈妈参加亲子游戏,在一个二维矩阵(N*N)的格子地图上,宝宝和妈妈抽签决定各自的位置,地图上每个格子有不同的糖果数量,部分格子有障碍物。 游戏规则是妈妈必须在最短的时间(每个单位时间只能走一步)到达宝宝的位置,路上的所有糖果都可以拿走,不能走障…...

大模型显存占用分析
kvcache显存占用分析 假设序列输入长度:s,输出长度:n,数据类型以FP16来保存KV cache。 峰值显存占用:b(sn)hl2*24blh(sn) 注:b表示batch size,第一个2表示k/v cache,第二个2表示FP1…...

matlab中旋转矩阵函数
文章目录 matlab里的旋转矩阵、四元数、欧拉角四元数根据两向量计算向量之间的旋转矩阵和四元数欧拉角转旋转矩阵旋转矩阵转欧拉角旋转矩阵转四元数参考链接 matlab里的旋转矩阵、四元数、欧拉角 旋转矩阵dcmR四元数quatq[q0,q1,q2,q3]欧拉角angle[row,pitch,yaw] % 旋转矩阵…...

探讨Spring Boot的自动配置原理
Spring Boot以其简化Spring应用开发和部署的能力而广受欢迎。其中最引人注目的特性之一就是自动配置,它极大地减少了开发者需要手动编写的配置量。在本篇博客中,我们将深入探讨Spring Boot自动配置的工作原理,以及它是如何使得Spring应用的配…...

【LeetCode】热题100 刷题笔记
文章目录 T1 两数之和T49 字母异位词分组常用小技巧 T1 两数之和 链接:1. 两数之和 题目: 【刷题感悟】这道题用两层for循环也能做出来,但我们还是要挑战一下时间复杂度小于 O ( n 2 ) O(n^2) O(n2)的解法,不能因为它是第一道 …...
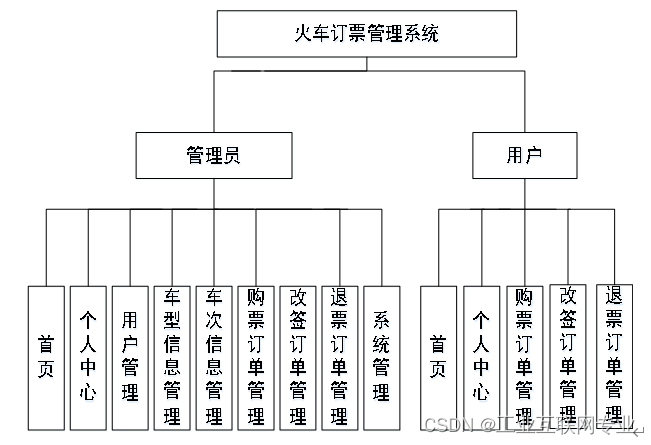
基于springboot+vue+Mysql的火车订票管理系统
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
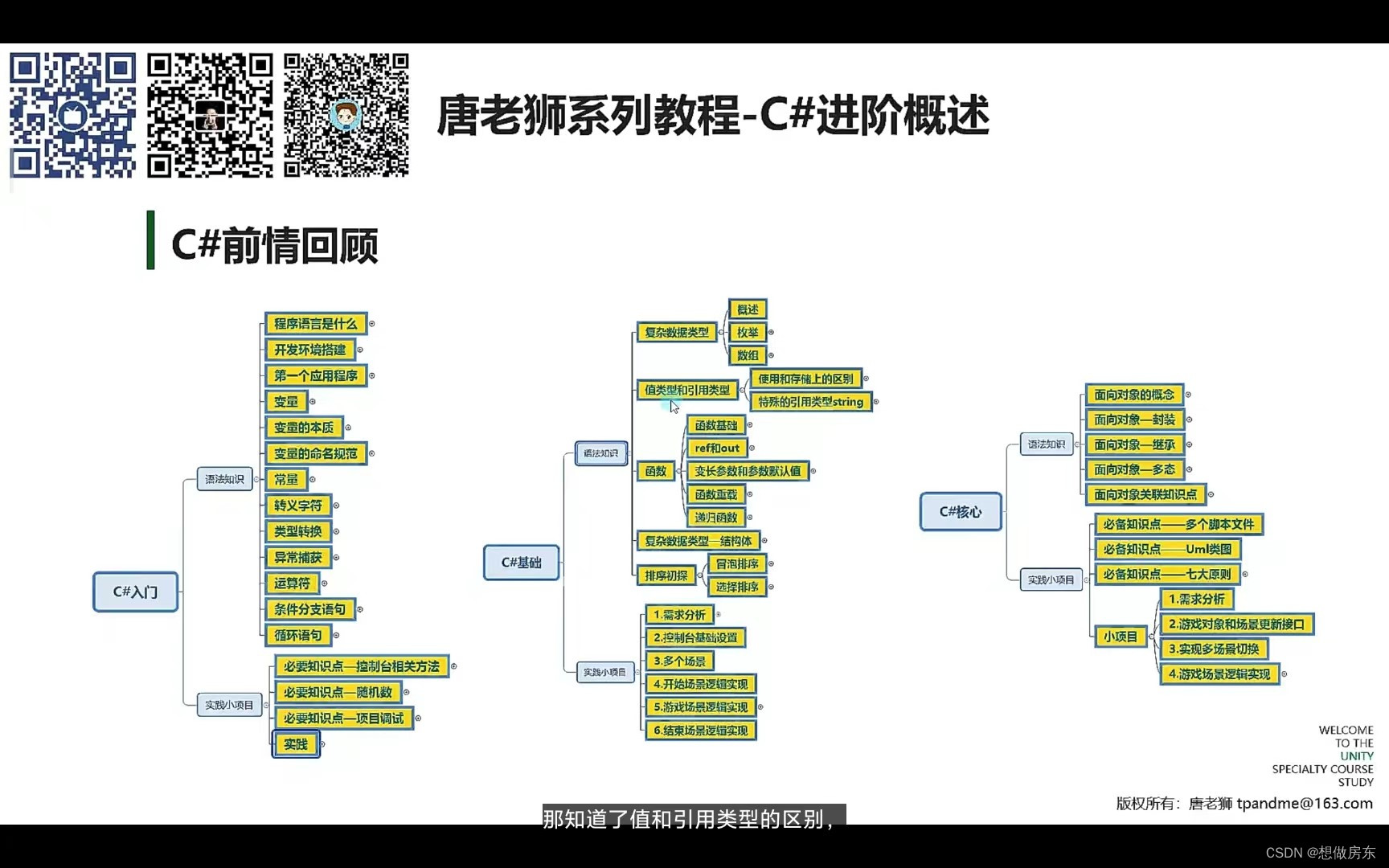
C#学习笔记 面试提要
冒泡 for (int m 0; m < arr.Length; m) { for (int n 0; n < arr.Length - 1 - m; n) { if (arr[n] > arr[n1]) { int temp arr[n]; arr[n] arr[n 1]; arr[n1] temp; } } } 选择 for (int m 0; m < arr.Length; m) { int index 0; for (int n 1; n < …...

Linux用户识别与身份验证命令一览
这些命令在系统管理、用户管理和监控工作中扮演着重要的角色。下面,介绍它们的类型及功能描述: 一、系统信息命令 hostname:此命令用于显示系统的主机名,它代表了系统在网络中的唯一标识。hostname -f:此命令进一步展…...
)
【Linux】GCC编译器(七)
文章目录 初步了解安装 GCC编译第一个程序编译选项 初步了解 GCC是GNU Compiler Collection的缩写,是一个由GNU项目开发的编译器集合。 GCC的历史和发展:GCC最初由理查德斯托曼(Richard Stallman)发起,目的是创建一个…...
【目录整理】(五)
Git 基础 Git 详细安装教程文章浏览阅读10w次,点赞9.6k次,收藏1.7w次。Git 是个免费的开源分布式版本控制系统,下载地址为git-scm.com 或者 gitforwindows.org,本文介绍 Git-2.40.0-64-bit.exe 版本的安装方法&#x…...

项目:USB键盘和鼠标的复合设备
我们的复合设备使用一个物理设备就可以完成多个功能。 使用复合设备同时完成USB键盘和鼠标功能,它的主要实现方式有两种, 第一个就是我们将多个设备描述符合并成一个,这个相对比较简单,我们只要根据相应的报告描述符处理数据就可…...
Linux利用Jenkins部署SpringBoot项目保姆级教程
在当今快速发展的软件开发领域,持续集成和持续部署(CI/CD)已经成为提升开发效率、缩短产品上市时间的关键实践。Linux系统以其稳定性和开源友好性,成为众多开发者和企业的首选平台。而Spring Boot,作为一个轻量级的Jav…...

elementUI 输入框按回车刷新页面问题
分析原因: 当 el-form 表单内只有一个 el-input 输入框时,且type为text类型时,在输入框内按回车就会触发表单的提交事件。 而当 el-form 表单内有多个 el-input 输入框时,按回车不会执行任何操作。 使用.prevent修饰符来阻止默…...

C++的字节对齐
什么是字节对齐 参考什么是字节对齐,为什么要对齐? 现代计算机中,内存空间按照字节划分,理论上可以从任何起始地址访问任意类型的变量。但实际中在访问特定类型变量时经常在特定的内存地址访问,这就需要各种类型数据按照一定的规…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
