C语言:二叉树的构建
目录
一、二叉树的存储
1.1 顺序存储
1.2 链式存储
二、二叉树的顺序结构及实现
2.1堆的概念及结构
2.2堆的构建
2.3堆的插入
2.4堆顶的删除
2.5堆的完整代码
三、二叉树的链式结构及实现
3.1链式二叉树的构建
3.2链式二叉树的遍历
3.2.1前序遍历
3.2.2中序遍历
3.2.3后序遍历
3.2.4层序遍历
一、二叉树的存储
二叉树一般用顺序结构存储或链式结构存储。
1.1 顺序存储
顺序存储就是用数组来存储,但一般使用数组只适合用来表示完全二叉树,如果不是完全二叉树,就可能存在空间浪费,甚至极大的空间浪费。二叉树的顺序存储在物理结构上是数组,在逻辑上是一颗二叉树。
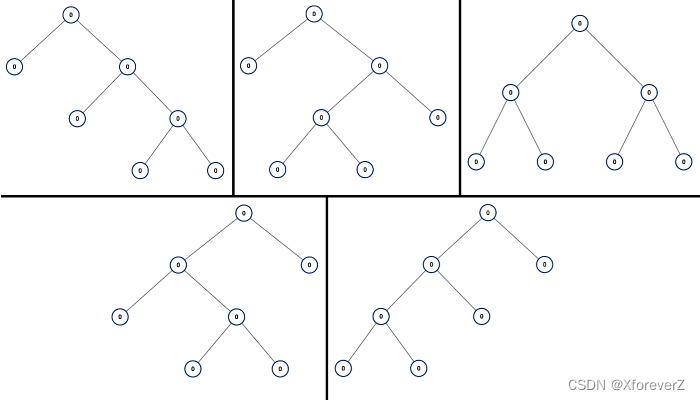
例:1、完全二叉树

2、非完全二叉树
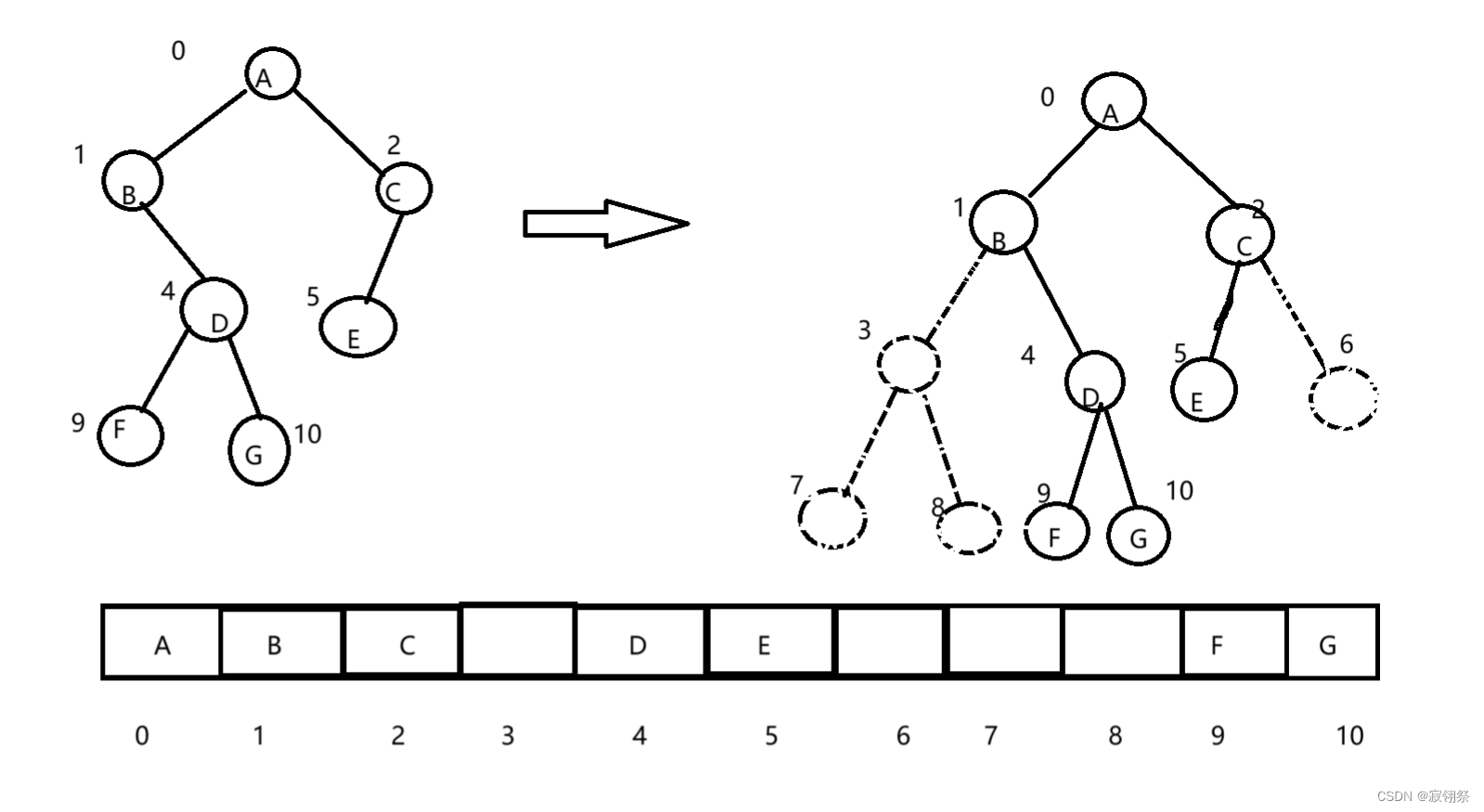
由上面两幅图可以看出,如果二叉树是非完全二叉树,则在数组中会存在很多空位,导致空间浪费。
1.2 链式存储
链式存储就是用链表来表示二叉树,一般用结构体表示每一个节点,每个节点中有三个域,数据域和左右指针域。数据域用来存储节点的数据,左指针指向左孩子,右指针指向右孩子。

二、二叉树的顺序结构及实现
在现实中,一般的二叉树用顺序存储可能会存在大量空间浪费,所以一般只用堆来用顺序结构存储。
注:这里的堆与地址空间中的堆不同,前者是数据结构,后者是操作系统中的一块内存区域分段。

2.1堆的概念及结构
1.概念:如果有一个集合K,将它的所有元素按照完全二叉树的顺序存储方式存储在一个一维数组中,并满足K(i)<=K(2*i+1)且K(i)<=K(2*i+1),则称为小堆,如果大于等于就是大堆。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
2.性质:
堆中某个节点的值总是不大于或不小于其父节点的值。
堆总是一颗完全二叉树。
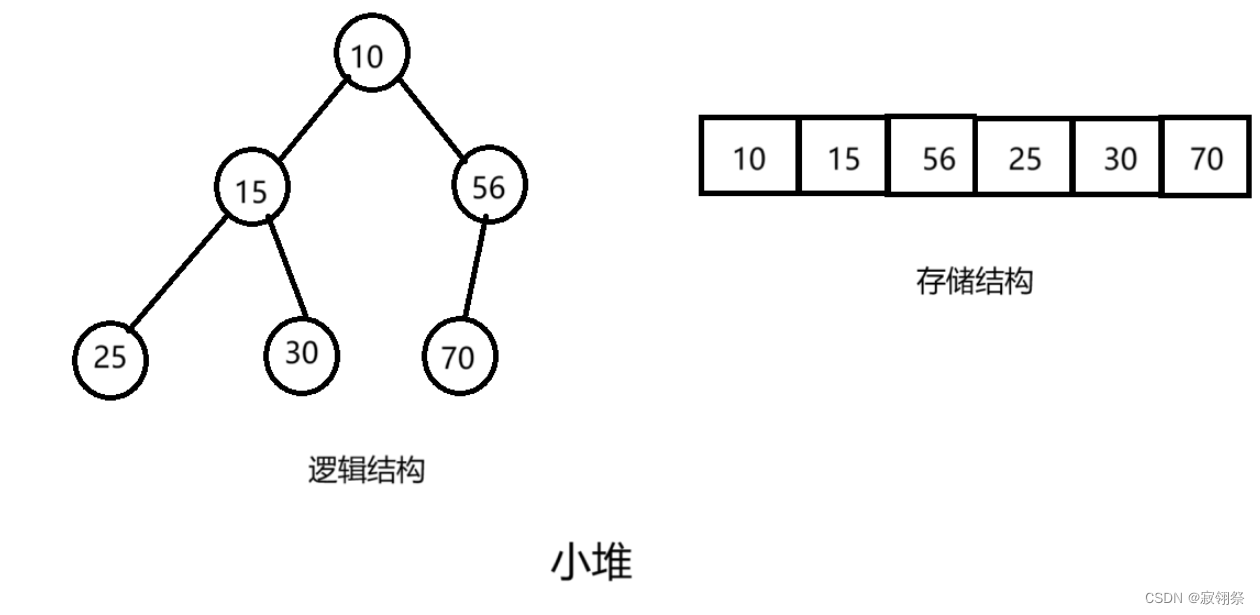

2.2堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);//断言堆是否存在hp->_a = NULL;//将数据置为空hp->_capacity = 0;//将堆的容量清零hp->_size = 0;//将堆的大小清零
}2.3堆的插入
void AdjustUp(HPDataType* a, int child)//向上调整堆
{int parent = (child - 1) / 2;//父节点在孩子节点-1除2的位置while (child>0)//如果孩子节点的位置不在最上面{if (a[child] < a[parent])//如果父节点小于孩子节点{swap(&a[child], &a[parent]);//交换值child = parent;parent = (child - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//断言堆是否存在if (hp->_size == hp->_capacity)//如果堆的大小等于容量,需扩容{size_t newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* tmp = realloc(hp->_a, sizeof(HPDataType) * newcapacity);//定义临时变量扩容if (tmp == NULL)//判断扩容是否成功{perror("realloc fail");//扩容失败return;}hp->_a = tmp;//将变量传给ahp->_capacity = newcapacity;//扩容}hp->_a[hp->_size] = x;//将值插入堆的最后hp->_size++;//堆的大小加1AdjustUp(hp->_a ,hp->_size -1);//用向上调整的方法重新调整堆,防止插入后不再是大堆或小堆
}2.4堆顶的删除
void AdjustUp(HPDataType* a, int child)//向下调整堆
{int parent = (child - 1) / 2;//父节点在孩子节点-1除2的位置while (child>0)//如果孩子节点的位置不在最上面{if (a[child] < a[parent])//如果父节点小于孩子节点{swap(&a[child], &a[parent]);//交换值child = parent;parent = (child - 1) / 2;}else{break;}}
}
// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);//断言堆是否存在assert(hp->_size > 0);//断言堆的大小是否为0swap(&hp->_a[0], &hp->_a[hp->_size - 1]);//交换堆顶和堆尾的值hp->_size--;//堆的大小减1AdjustDown(hp->_a, hp->_size, 0);//向下调整堆
}2.5堆的完整代码
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);//断言堆是否存在hp->_a = NULL;//将数据置为空hp->_capacity = 0;//将堆的容量清零hp->_size = 0;//将堆的大小清零
}// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);//断言堆是否存在free(hp->_a);//释放数据hp->_a = NULL;//将指针置为空hp->_capacity = 0;将堆的容量清零hp->_size = 0;//将堆的大小清零
}
void swap(HPDataType* x, HPDataType* y)
{HPDataType tmp = *x;*x = *y;*y = tmp;
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//左孩子节点是父亲节点的2倍加1while (child < n)//如果孩子节点不在最后{//找到左右孩子中较小的if (child + 1 < n && a[child + 1] < a[child])//如果左孩子大于右孩子{++child;}if (a[child] < a[parent])//如果孩子小于父亲{swap(&a[child], &a[parent]);//交换父节点与子节点parent = child;child = parent * 2 + 1;}else{break;}}
}void AdjustUp(HPDataType* a, int child)//向上调整堆
{int parent = (child - 1) / 2;//父节点在孩子节点-1除2的位置while (child>0)//如果孩子节点的位置不在最上面{if (a[child] < a[parent])//如果父节点小于孩子节点{swap(&a[child], &a[parent]);//交换值child = parent;parent = (child - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//断言堆是否存在if (hp->_size == hp->_capacity)//如果堆的大小等于容量,需扩容{size_t newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* tmp = realloc(hp->_a, sizeof(HPDataType) * newcapacity);//定义临时变量扩容if (tmp == NULL)//判断扩容是否成功{perror("realloc fail");//扩容失败return;}hp->_a = tmp;//将变量传给ahp->_capacity = newcapacity;//扩容}hp->_a[hp->_size] = x;//将值插入堆的最后hp->_size++;//堆的大小加1AdjustUp(hp->_a ,hp->_size -1);//用向上调整的方法重新调整堆,防止插入后不再是大堆或小堆
}// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);//断言堆是否存在return hp->_a[0];
}// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);//断言堆是否存在assert(hp->_size > 0);//断言堆的大小是否为0swap(&hp->_a[0], &hp->_a[hp->_size - 1]);//交换堆顶和堆尾的值hp->_size--;//堆的大小减1AdjustDown(hp->_a, hp->_size, 0);//向下调整堆
}// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}// 对数组进行堆排序
void HeapSort(int* a, int n)
{for (int i = (n - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}
}三、二叉树的链式结构及实现
一颗链式二叉树一般用结构体表示,结构体中一个存储数据,一个链表指向左孩子节点,一个指向右孩子节点。
typedef int BTDataType;//方便后面改变二叉树中的数据类型typedef struct BinaryTreeNode
{BTDataType data;//二叉树存储数据的节点struct BinaryTreeNode* left;//左孩子节点struct BinaryTreeNode* right;//右孩子节点
}BTNode;//重命名3.1链式二叉树的构建
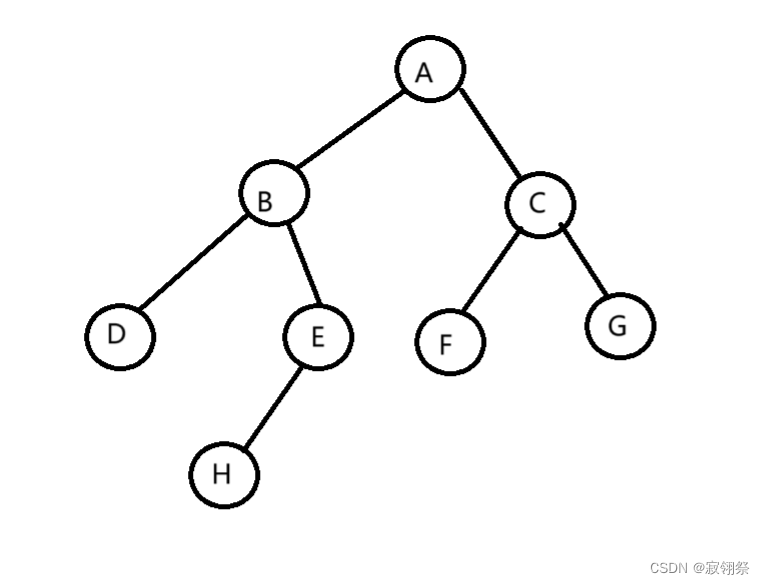
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)//二叉树一般需要手动扩建
{BTNode* n1 = BuyNode('A');BTNode* n2 = BuyNode('B');BTNode* n3 = BuyNode('C');BTNode* n4 = BuyNode('D');BTNode* n5 = BuyNode('E');BTNode* n6 = BuyNode('F');BTNode* n7 = BuyNode('G');BTNode* n8 = BuyNode('H');n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;n5->left = n8;return n1;
}
3.2链式二叉树的遍历
二叉树的遍历就是按照某种特殊规则,依次对二叉树的节点进行操作,每个节点只能操作一次。
二叉树的遍历一般有4种方式。
3.2.1前序遍历
前序遍历:优先操作每个节点的自身,后操作左节点,最后操作右节点。

例如上图的树就是按照A-B-D-E-H-C-F-G的顺序操作。
从A开始,先操作A的自身,再访问A的左节点B。
B节点先操作自身,再访问B的左节点D。
D节点操作自身,无孩子节点则返回到B,访问B的右节点E。
E节点操作自身,再访问E的左节点H。
H节点操作自身,无孩子节点则返回到E,E无左孩子节点则返回到B,B的左右孩子都已访问则返回到A,访问A的右节点C。
C节点操作自身,再访问C的左节点F。
F节点操作自身,无孩子节点则返回C,访问C的右节点G
G节点操作自身,无孩子节点,访问结束。
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");//如果节点为空打印Nreturn;}printf("%c ", root->data);//打印节点BinaryTreePrevOrder(root->left);//访问左节点BinaryTreePrevOrder(root->right);//访问右节点
}3.2.2中序遍历
中序遍历:优先操作每个节点的左节点,后操作自身,最后操作右节点。

上图按照D-B-H-E-A-F-C-G的顺序操作。
从A开始,先访问A的左节点B,B节点先访问D,D无左节点,操作自身。
D无右节点,则返回B,操作B的自身,再访问B的右节点E。
E节点先访问左节点H,H无左节点,操作自身,H无右节点,则返回E节点。
E节点操作自身,无右节点,返回B节点,再返回A节点。
A节点操作自身,再访问右节点C,C节点访问左节点F。
F无左节点操作自身,无右节点,返回C节点。
C节点操作自身,再访问C的右节点G。
G无左节点,操作自身,无右节点,访问结束。
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N ");//如果节点为空打印Nreturn;}BinaryTreePrevOrder(root->left);//访问左节点printf("%c ", root->data);//打印节点BinaryTreePrevOrder(root->right);//访问右节点
}3.2.3后序遍历
后序遍历:优先操作每个节点的左节点,后操作右节点,最后操作自身。

上图按照D-B-H-E-F-C-G-A的顺序操作。
从A开始,访问A的左节点B,再访问B的左节点D,D无左右节点,操作自身,返回B节点。
访问B节点的右节点E,再访问E的左节点H,H无左右节点, 操作自身,返回E节点。
E节点操作自身,返回B节点。
B节点操作自身,返回A节点,再访问A节点的右节点C,访问C的左节点F。
F无左右节点,操作自身,返回C节点,访问C节点的右节点G。
G无左右节点,操作自身,返回C节点。
C节点操作自身,返回A节点。
A节点操作自身,访问结束。
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");//如果节点为空打印Nreturn;}BinaryTreePrevOrder(root->left);//访问左节点BinaryTreePrevOrder(root->right);//访问右节点printf("%c ", root->data);//打印节点
}3.2.4层序遍历
层序遍历:按照二叉树的每一层,一层一层的从左向右操作。
实现二叉树的层序遍历需要用到队列的知识。
队列是一个有着先进先出原则的链表,先进的元素永远比后进的元素先出来。通过队列的规则,只要二叉树的每一个节点出队列时将其左右孩子节点入队列即可完成二叉树的层序遍历。

上图的操作顺序是A-B-C-D-E-F-G-H
A节点入队列,A节点出队列,将A的左右子节点BC入队列。
此时队列中有B-C,将B出队列,B的左右子节点DE入队列。
此时队列中有C-D-E,将C出队列,C的左右子节点FG入队列。
此时队列中有D-E-F-G,将D出队列,D无子节点。
此时队列中有E-F-G,将F出队列,F的左节点H入队列。
此时队列中有F-G-H,均无子节点,一个一个出队列即可。
队列头文件代码
#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<assert.h>
#include<string.h>
#include<stdlib.h>
typedef struct BinTreeNode* QDataType;
// 链式结构:表示队列
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;
// 队列的结构
typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);
队列代码
#include"1.h"// 初始化队列
void QueueInit(Queue* q)
{assert(q);//断言队列是否存在q->phead = NULL;//将头节点的置为空q->ptail = NULL;//将尾节点置为空q->size = 0;//将队列大小初始化为0
}// 队尾入队列
void QueuePush(Queue* pq, QDataType x)
{assert(pq);//断言队列是否存在QNode* newnode = (QNode*)malloc(sizeof(QNode));//创建临时变量if (newnode == NULL)//判断变量是否创建成功{perror("malloc fail");return;}newnode->data = x;//将要入队列的值给临时变量newnode->next = NULL;//将临时变量的指向下一个节点的指针置空if (pq->ptail)//如果尾队列存在,则队列中含有数据{pq->ptail->next = newnode;//将原本尾队列指向下一个节点的指针指向临时变量pq->ptail = newnode;//将临时变量设为尾节点}else//尾队列不存在,则队列为空{pq->phead = pq->ptail = newnode;//将头节点和尾节点都设为临时变量}pq->size++;//队列大小加1
}// 队头出队列
void QueuePop(Queue* q)
{assert(q);//断言队列是否存在assert(q->phead != NULL);//断言队列的头节点是否为空if (q->phead->next == NULL)//队列头节点的下一个节点为空,则队列中只有一个元素{free(q->phead);//释放头节点q->phead = q->ptail = NULL;//将头节点和尾节点置空}else//队列中不止1个元素{QNode* next = q->phead->next;//创建临时变量指向头节点的下一个节点free(q->phead);//是否头节点q->phead = next;//将头节点的下一个节点设为头节点}q->size--;//队列大小减1
}// 获取队列头部元素
QDataType QueueFront(Queue* q)
{assert(q);//断言队列是否存在assert(q->phead != NULL);//断言队列的头节点是否为空return q->phead->data;//返回队列头节点的数据
}// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{assert(q);//断言队列是否存在assert(q->ptail != NULL);//断言队列的尾节点是否为空return q->ptail->data;//返回队列尾节点的数据
}// 获取队列中有效元素个数
int QueueSize(Queue* q)
{assert(q);//断言队列是否存在return q->size;//返回队列的大小
}// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{assert(q);//断言队列是否存在return q->size == 0;//判断队列的大小是否为0
}// 销毁队列
void QueueDestroy(Queue* q)
{assert(q);//断言队列是否存在QNode* cur = q->phead;//定义临时节点等于头节点while (cur)//如果头节点不为空{QNode* next = cur->next;//定义临时节点指向头节点的下一个节点free(cur);//释放头节点cur = next;//将下一个节点当作头节点}q->phead = NULL;//将头节点指针置空q->ptail = NULL;//将尾节点指针置空q->size = 0;//将队列大小置为0
}二叉树头文件
#pragma once
#include<stdio.h>
#include<string.h>
#include<assert.h>
#include<stdlib.h>
typedef int BTDataType;//方便后面改变二叉树中的数据类型typedef struct BinaryTreeNode
{BTDataType data;//二叉树存储数据的节点struct BinaryTreeNode* left;//左孩子节点struct BinaryTreeNode* right;//右孩子节点
}BTNode;//重命名#include"1.h"// 通过前序遍历的数组"ABD##E#H##CF##G##"构建 二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);二叉树代码
#include"tree.h"
BTNode* BuyNode(BTDataType a)//a是要创建的值
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));//定义临时变量扩容if (newnode == NULL){printf("malloc fail");//扩容失败return NULL;}newnode->data = a;newnode->left = NULL;newnode->right = NULL;return newnode;
}
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)//二叉树一般需要手动扩建
{BTNode* n1 = BuyNode('A');BTNode* n2 = BuyNode('B');BTNode* n3 = BuyNode('C');BTNode* n4 = BuyNode('D');BTNode* n5 = BuyNode('E');BTNode* n6 = BuyNode('F');BTNode* n7 = BuyNode('G');BTNode* n8 = BuyNode('H');n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;n5->left = n8;return n1;
}// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{assert(root);free(root);}// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 :BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* ret1= BinaryTreeFind(root->right, x);if (ret1){return ret1;}BTNode* ret2=BinaryTreeFind(root->left , x);if (ret2){return ret2;}return NULL;
}// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");//如果节点为空打印Nreturn;}printf("%c ", root->data);//打印节点BinaryTreePrevOrder(root->left);//访问左节点BinaryTreePrevOrder(root->right);//访问右节点
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N ");//如果节点为空打印Nreturn;}BinaryTreePrevOrder(root->left);//访问左节点printf("%c ", root->data);//打印节点BinaryTreePrevOrder(root->right);//访问右节点
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");//如果节点为空打印Nreturn;}BinaryTreePrevOrder(root->left);//访问左节点BinaryTreePrevOrder(root->right);//访问右节点printf("%c ", root->data);//打印节点
}
// 层序遍历
void TreeLevelOrder(BTNode* root)
{Queue q;//定义临时节点QueueInit(&q);//创建临时节点if (root)//如果节点不为空{QueuePush(&q, root);//节点入队列}while (!QueueEmpty(&q))//如果队列不为空{BTNode* front = QueueFront(&q);//获取队头元素QueuePop(&q);//队头元素出队列if (front)//如果节点存在{printf("%d ", front->data);//打印节点数据// 带入下一层QueuePush(&q, front->left);//左孩子节点入队列QueuePush(&q, front->right);//右孩子节点入队列}else{printf("N ");//不存在打印N}}printf("\n");QueueDestroy(&q);//销毁临时节点,防止空间泄露
}相关文章:

C语言:二叉树的构建
目录 一、二叉树的存储 1.1 顺序存储 1.2 链式存储 二、二叉树的顺序结构及实现 2.1堆的概念及结构 2.2堆的构建 2.3堆的插入 2.4堆顶的删除 2.5堆的完整代码 三、二叉树的链式结构及实现 3.1链式二叉树的构建 3.2链式二叉树的遍历 3.2.1前序遍历 …...

软件测试工程师面试汇总功能测试篇
Q:一、进行测试用例设计的时候用到的方法有哪些? A:最常使用的测试用例设计方法包括等价类划分法、边界值分析方法、场景法、错误推测法。其中,最容易 发现错误的是边界值法,使用最多的是场景法。以注册为例:首先从需求确定用户名…...

javaAPI1
API application pragramming interface 应用程序编程接口 除java.lang包以外,其他包中的类在使用时需要导入 建包 package com.abc.javabean; 导包格式,import 包名.类名 API使用技巧 1,先看关键字 2,看参数列表 3,看返回值类型 String 封装字符串和处理字符串的类…...

案例研究|DataEase实现物业数据可视化管理与决策支持
河北隆泰物业服务有限责任公司(以下简称为“隆泰物业”)创建于2002年,总部设在河北省高碑店市,具有国家一级物业管理企业资质,通过了质量体系、环境管理体系、职业健康安全管理体系等认证。自2016年至今,隆…...
Android Studio Iguana | 2023.2.1 补丁 1
Android Studio Iguana | 2023.2.1 Canary 3 已修复的问题Android Gradle 插件 问题 295205663 将 AGP 从 8.0.2 更新到 8.1.0 后,任务“:app:mergeReleaseClasses”执行失败 问题 298008231 [Gradle 8.4][升级] 由于使用 kotlin gradle 插件中已废弃的功能&#…...

iOS17 隐私协议适配详解
1. 背景 网上搜了很多文章,总算有点头绪了。其实隐私清单最后做出来就是一个plist文件。找了几个常用三方已经配好的看了看,比着做就好了。 WWDC23 中关于隐私部分的更新(WWDC23 隐私更新官网),其中提到了第三方 SDK 的…...
LeetCode 每日一题 Day 116-122
2580. 统计将重叠区间合并成组的方案数 给你一个二维整数数组 ranges ,其中 ranges[i] [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。 你需要将 ranges 分成 两个 组(可以为空…...

linux离线安装jenkins及使用教程
本教程采用jenkins.war的方式离线安装部署,在线下载的方式会遇到诸多问题,不宜采用 基本环境: 1.jdk环境,Jenkins是java语言开发的,因需要jdk环境。 2.git/svn客户端,因一般代码是放在git/svn服务器上的&a…...
NXP-S32DS软件安装
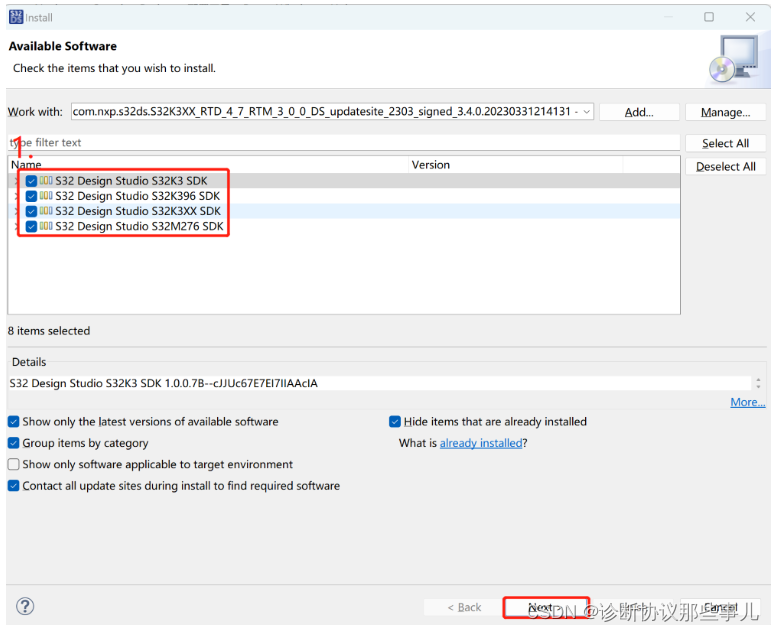
文章目录 一、安装包获取二、S32DS安装三、芯片插件安装 一、安装包获取 登录NXP官网,进入软件目录https://www.nxp.com/ 下载S32DS软件和RTD驱动库,并安装S32DS软件。 单击“S32DS.3.5_b220726_win32.x86_64.exe”下载该软件 点击“License Keys”&…...
26版SPSS操作教程(初级第十五章)
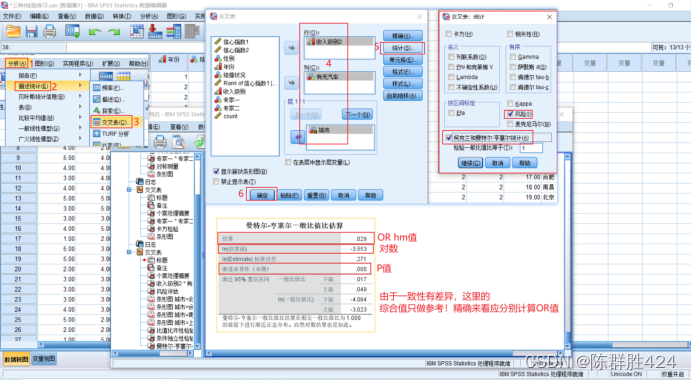
前言 #由于导师最近布置了学习SPSS这款软件的任务,因此想来平台和大家一起交流下学习经验,这期推送内容接上一次第十四章的学习笔记,希望能得到一些指正和帮助~ 粉丝及官方意见说明 #针对官方爸爸的意见说的推送缺乏操作过程的数据案例文件…...
docker部署实用的运维开发手册
下载镜像 docker pull registry.cn-beijing.aliyuncs.com/wuxingge123/reference:latestdocker-compose部署 vim docker-compose.yml version: 3 services:reference:container_name: referenceimage: registry.cn-beijing.aliyuncs.com/wuxingge123/reference:latestports:…...

Oracle VM(虚拟机)性能监控工具
Oracle VM是一个独立的虚拟化环境,由 Oracle 提供支持和设计,旨在为运行虚拟机提供轻量级、安全的基于服务器的平台。Oracle VM 能够在受支持的虚拟化环境中部署操作系统和应用软件,Oracle VM 将用户和管理员与底层虚拟化技术隔离开来&#x…...
1.8 python 模块 time、random、string、hashlib、os、re、json
ython之模块 一、模块的介绍 (1)python模块,是一个python文件,以一个.py文件,包含了python对象定义和pyhton语句 (2)python对象定义和python语句 (3)模块让你能够有逻辑地…...

iOS苹果签名共享签名是什么以及如何获取?
哈喽,大家好呀,咕噜淼淼又来和大家见面啦,最近有很多朋友都来向我咨询共享签名iOS苹果IPA共享签名是什么,针对这个问题,淼淼来解答一下大家的疑惑并告诉大家iOS苹果ipa共享签名需要如何获取。 现在苹果签名在市场上的…...

python爬虫下载音乐
本文使用创作助手。 你可以使用Python的requests库来实现爬虫下载音乐。以下是一个简单的示例代码: import requestsdef download_music(url, file_path):response requests.get(url)with open(file_path, wb) as file:file.write(response.content)print(f"…...

HarmonyOS实战开发-一次开发,多端部署-视频应用
介绍 随着智能设备类型的不断丰富,用户可以在不同的设备上享受同样的服务,但由于设备形态不尽相同,开发者往往需要针对具体设备修改或重构代码,以实现功能完整性和界面美观性的统一。OpenHarmony为开发者提供了“一次开发&#x…...
关于v114之后的chromedriver及存放路径
使用selenium调用浏览器时,我一直调用谷歌浏览器,可浏览器升级后,就会再次遇到以前遇到过的各种问题,诸如:1、怎么关闭浏览器更新;2、去哪儿下载chromedriver;3、114版本之后的驱动去哪儿下载&a…...
http模块 服务器端如何响应(获取)静态资源?
一、静态资源与动态资源介绍: (1)静态资源 内容长时间不改变的资源。eg:图片、视频、css js html文件、字体文件... (2)动态资源 内容经常更新的资源。eg:百度首页、淘宝搜索列表... 二、服…...
基于PHP的校园招聘管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的校园招聘管理系统 一 介绍 此校园招聘管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为个人用户,企业和管理员三种。 技术栈:phpmysqlbootstrapphpstudyvscode 二…...

LLMs 可能在 2 年内彻底改变金融行业
在艾伦图灵研究所(The Alan Turing Institute)最新的一项研究中,我们看到了大型语言模型(Large Language Models,LLMs)的一种可能性。它有望通过检测欺诈行为、生成财务洞察以及自动化客户服务,…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
