小于n的最大数 Leetcode 902 Numbers At Most N Given Digit Set
这两个问题的本质就是一个棵树,然后根据n对树做剪枝。难点在于剪的时候边界条件有些坑,get_lower_largest_digit_dic是这两个题目的共同点
题目一: 小于n的最大数
算法题目:小于n的最大数
问题描述:给一个数组nums=[5,4,8,2],给一个n=5416, 让你从nums中选出一些元素,使得组成的数字是小于n的最大数,比如这个例子应该返回5288
这个题其实就是回溯一步,但是讨论的情况有点绕,细节可以看代码
class Solution:def get_num(self, candidates, num):max_str = str(max(list(candidates)))num_str = str(num)def get_lower_largest_digit_dic(candidates):dic={}prev = Nonefor i in range(10):dic[str(i)] = previf i in candidates:prev = str(i)return diclower_largest_digit_dic = get_lower_largest_digit_dic(candidates)i,l = 0,len(num_str)res_str_arr = ['0' for i in range(l)]while(i<l):if int(num_str[i]) in candidates and i<l-1:# 第一阶段,相等的一直往后填res_str_arr[i] = num_str[i]i += 1else:# 第二阶段:遇到最后一个,或者没有相等的(也分为几种情况),统一填为lower_largest_digit,然后后面统一填最大digit = lower_largest_digit_dic[num_str[i]]while digit == None and i > 0: #一直找不到,一直回溯i -= 1digit = lower_largest_digit_dic[num_str[i]]# 按照while不成功的情况讨论下if i == 0 and digit == None and l == 1:return Noneif i == 0 and digit == None and l > 1:res_str_arr[0] = '0'else:res_str_arr[i] = digitfor j in range(i+1,l):res_str_arr[j] = max_strreturn int(''.join(res_str_arr))if __name__ == '__main__':s = Solution()print(s.get_num({1,2,9,4}, 2533)) # 2499print(s.get_num({1,2,5,4}, 2543)) # 2542print(s.get_num({1,2,5,4}, 2541)) # 2525print(s.get_num({1,2,9,4}, 2111)) # 1999print(s.get_num({5,9}, 5555)) #999
题目二: 最大为 N 的数字组合
来自https://leetcode.com/problems/numbers-at-most-n-given-digit-set/
Given an array of digits which is sorted in non-decreasing order. You can write numbers using each digits[i] as many times as we want. For example, if digits = [‘1’,‘3’,‘5’], we may write numbers such as ‘13’, ‘551’, and ‘1351315’.
Return the number of positive integers that can be generated that are less than or equal to a given integer n.
Example 1:
Input: digits = [“1”,“3”,“5”,“7”], n = 100
Output: 20
Explanation:
The 20 numbers that can be written are:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.
Example 2:
Input: digits = [“1”,“4”,“9”], n = 1000000000
Output: 29523
Explanation:
We can write 3 one digit numbers, 9 two digit numbers, 27 three digit numbers,
81 four digit numbers, 243 five digit numbers, 729 six digit numbers,
2187 seven digit numbers, 6561 eight digit numbers, and 19683 nine digit numbers.
In total, this is 29523 integers that can be written using the digits array.
Example 3:
Input: digits = [“7”], n = 8
Output: 1
Constraints:
1 <= digits.length <= 9
digits[i].length == 1
digits[i] is a digit from ‘1’ to ‘9’.
All the values in digits are unique.
digits is sorted in non-decreasing order.
1 <= n <= 109
其实和题目一思路很相似,但是边界条件容易错:
class Solution:def atMostNGivenDigitSet(self, digits: List[str], n: int) -> int:def get_lt_digit_cnt_dic(digits_set):dic = {}prev = 0for i in range(0,10):stri = str(i)dic[stri] = previf stri in digits_set:prev += 1return dicdigits_set = set(digits)lt_digit_cnt_dic = get_lt_digit_cnt_dic(digits_set)dl = len(digits)nl = len(str(n))factorial = [1 for i in range(nl)]for i in range(1,nl):factorial[i] = factorial[i-1]*dlres1 = sum(factorial[i] for i in range(1,nl))res2,i = 0,0strn = str(n)while i<nl:lt_digit_cnt = lt_digit_cnt_dic[strn[i]]res2 += lt_digit_cnt * factorial[nl-(i+1)]if (strn[i] not in digits_set):breaki+=1# 这个条件容易漏掉,例如digits =["3","4","8"], n = 4if i == nl and strn[nl-1] in digits_set:res2 += 1# print(res1)return res1+res2
相关文章:

小于n的最大数 Leetcode 902 Numbers At Most N Given Digit Set
这两个问题的本质就是一个棵树,然后根据n对树做剪枝。难点在于剪的时候边界条件有些坑,get_lower_largest_digit_dic是这两个题目的共同点 题目一: 小于n的最大数 算法题目:小于n的最大数 问题描述:给一个数组nums[5…...

Leetcode刷题-数组(二分法、双指针法、窗口滑动)
数组 1、二分法 704. 二分查找 - 力扣(LeetCode) 需要注意区间的问题。首先在最外面的循环判断条件是left<right。那就说明我们区间规定的范围就是【left,right】 属于是左闭右闭!!!!!&…...

STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (b)
继续上篇博文:STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (a)-CSDN博客 往下写, 为什么:当GPIO_InitStructure.GPIO_PinGPIO_Pin_0 ; 时,其实就是将对应的该引脚的寄存器地…...

数据仓库——事实表
数据仓库基础笔记思维导图已经整理完毕,完整连接为: 数据仓库基础知识笔记思维导图 事实表 事务事实表 事务事实表用于跟踪事件,通过存储事实和与之关联的维度细节,允许单独或聚集地研究行为。粒度稀疏性包含可加事实 无事实的…...

人工智能常用的编程语言有哪些?
人工智能常用的编程语言包括Python、Java、C、R、Lisp和Prolog等。具体选择取决于项目需求、技术背景和性能要求。 Python是AI领域的明星语言,由于其简洁易懂的语法、丰富的库支持以及庞大的社区资源,适用于机器学习、深度学习和自然语言处理等领域。 …...

【Leetcode每日一题】模拟 - 提莫攻击(难度⭐)(45)
1. 题目解析 题目链接:495. 提莫攻击 2.算法原理 一、分情况讨论 要计算中毒的总时长,我们需要考虑时间点之间的差值,并根据这些差值来确定中毒的实际持续时间。 情况一:差值大于等于中毒时间 假设你的角色在时间点A中毒&#…...
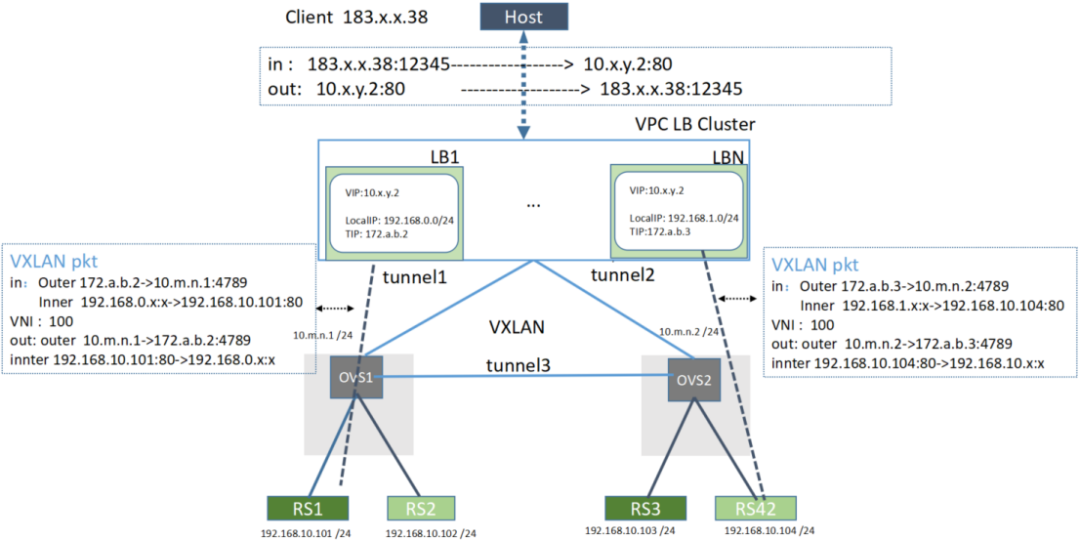
OPPO云VPC网络实践
1 OPPO 云网络现状 随着OPPO业务的快速发展,OPPO云规模增长迅速。大规模虚拟实例的弹性伸缩、低延时需求对网络提出了诸多挑战。原有基于VLAN搭建的私有网络无法解决这些问题,给网络运维和业务的快速上线带来了挑战。 梳理存在的主要问题如下…...
找到所有数组中消失的数字)
力扣(数组)找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 示例 1: 输入:nums [4,3,2,7,8,2,3,1] 输出:[5,6]示例 2&am…...
每日面经分享(Spring Boot: part3 Service层)
SpringBoot Service层的作用 a. 封装业务逻辑:Service层负责封装应用程序的业务逻辑。Service层是控制器(Controller)和数据访问对象(DAO)之间的中间层,负责处理业务规则和业务流程。通过将业务逻辑封装在S…...

k8s的pod访问service的方式
背景 在k8s中容器访问某个service服务时有两种方式,一种是把每个要访问的service的ip注入到客户端pod的环境变量中,另一种是客户端pod先通过DNS服务器查找对应service的ip地址,然后在通过这个service ip地址访问对应的service服务 pod客户端…...

shell脚本发布docker-nginx vue2 项目示例
docker、git、node.js安装略过。 使git pull或者git push不需要输入密码操作方法 nginx安装在docker容器里面,参见:https://blog.csdn.net/HSJ0170/article/details/128631155 姊妹篇(宿主机nginx,非docker-nginx)&am…...
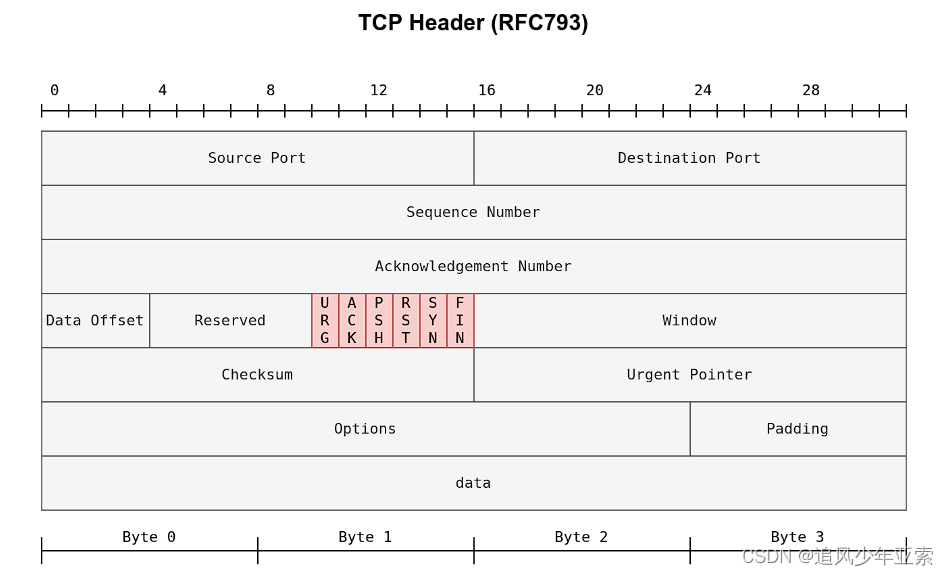
【THM】Nmap Basic Port Scans(基本端口扫描)-初级渗透测试
介绍 本房间是Nmap系列的第二个房间(网络安全简介模块的一部分)。 1.Nmap实时主机发现 2.Nmap基本端口扫描 3.Nmap高级端口扫描 4.Nmap后端口扫描 在之前的房间里,我们专注于发现在线系统。到目前为止,我们已经介绍了Nmap扫描的三个步骤: 枚举目标发现活动主机反向-…...

Groovy结合Java在生产中的落地实战
Groovy简介 Groovy是用于Java虚拟机的一种敏捷的动态语言,是一种成熟的面向对象编程语言,又是一种纯粹的脚本语言。Groovy运行在JVM环境上,在语法上兼具java 语言和脚本语言特点,大大简化了语法。同时又具有闭包和动态语言中的其…...

达梦数据库 创建外部表 [-7082]:外部表数据错误.
1:定义 外部表,是指不存在于数据库中的表。通过向达梦提供描述外部表的元数据,可以把一 个操作系统文件当成一个只读的数据库表,就像这些数据存储在一个普通数据库表中一样来 进行访问。 外部表的数据存储在操作系统中࿰…...
XUbuntu22.04之激活Linux最新Typora版本(二百二十五)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

JavaScript简介
目录 概要: 说明: 学习JS的原因: JS可以干什么: 了解JavaScript: 前言: JavaScript的历史: JavaScript与ECMAScript: 如何运行JavaScript以及JavaScrip的特点: …...

使用PaddleX实现的智慧农业病虫检测项目
目录 1. 数据集解压 2.检查数据集的图片是否均可读取 3. 查看数据集的类别信息...
算法学习——LeetCode力扣图论篇1(797. 所有可能的路径、200. 岛屿数量、695. 岛屿的最大面积)
算法学习——LeetCode力扣图论篇1 797. 所有可能的路径 797. 所有可能的路径 - 力扣(LeetCode) 描述 给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特…...

【IP组播】PIM-SM的RP、RPF校验
目录 一:PIM-SM的RP 原理概述 实验目的 实验内容 实验拓扑 1.基本配置 2.配置IGP 3.配置PIM-SM和静态RP 4.配置动态RP 5.配置Anycast RP 二: RPF校验 原理概述 实验目的 实验内容 实验拓扑 1.基本配置 2.配置IGP 3.配置PIM-DM 4.RPF校…...

前端代码规范-命名规范
命名规则 camelCase(小驼峰式命名法 —— 首字母小写)PascalCase(大驼峰式命名法 —— 首字母大写)kebab-case(短横线连接式)Snake(下划线连接式) 项目名称 项目名 全部采用小写方…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
