门控循环单元(GRU)
概述
门控循环单元(Gated Recurrent Unit, GRU)由Junyoung Chung等人于2014年提出,原论文为《Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling》。GRU是循环神经网络(Recurrent Neural Network, RNN)的一种,和LSTM(Long-Short Term Memory)一样,也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。其优势就在于,在有和LSTM相似的表现的情况下,比LSTM更简单,更容易训练或计算。
详解
重置门和更新门
我们首先介绍重置门(Reset Gate)和更新门(Update Gate)。所谓门就是一种控制单元,用来控制一个事物是有还是无。它们被设计成(0,1)区间中的向量来方便进行凸组合。所谓凸组合就是加权平均。
重置门用于控制前一个隐状态在当前时间步骤的计算中保留多少历史信息。重置门的输出接近于0表示较多地忽略前一个隐状态的信息,而接近于1表示较多地保留前一个隐状态的信息。
更新门用于控制当前时间步骤的候选隐状态(candidate hidden state)对最终的隐状态更新的贡献程度。更新门的输出接近于0表示较少地更新当前时间步骤的隐状态,而接近于1表示较多地更新当前时间步骤的隐状态。
这些门并不是人为指定的,而是机器通过当前时间步的输入和前一个隐状态进行学习得到的。下图描述了门控循环单元中的重置门和更新门的输入,输入是由当前时间步的输入和前一时间步的隐状态给出。两个门的输出是由使用sigmoid激活函数的两个全连接层给出。
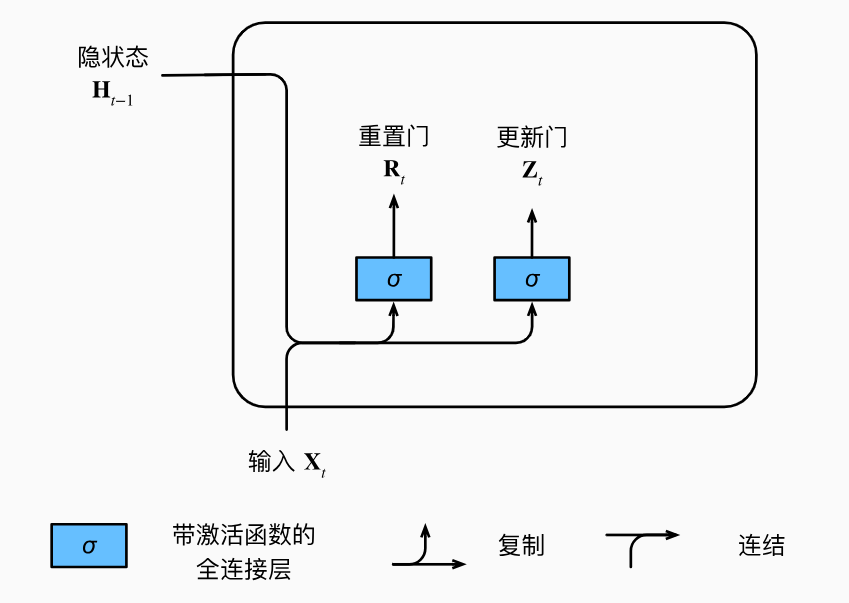
图中,输入和隐状态分别通过两个不同的带激活函数的全连接层得到两个门的值。这两个门将在后面发挥它们的控制效果,现在先来看一下他们的数学表达。对于给定的时间步 t t t,假设输入是一个小批量 X t ∈ R n × d \mathbf{X}_t\in\mathbb{R}^{n\times d} Xt∈Rn×d(样本个数n,输入个数d), 上一个时间步的隐状态是 H t − 1 ∈ R n × h \mathbf{H}_{t-1}\in\mathbb{R}^{n\times h} Ht−1∈Rn×h(隐藏单元个数h)。那么,重置门 R t ∈ R n × h \mathbf{R}_{t}\in\mathbb{R}^{n\times h} Rt∈Rn×h和更新门 Z t ∈ R n × h \mathbf{Z}_{t}\in\mathbb{R}^{n\times h} Zt∈Rn×h的计算如下所示:
R t = σ ( X t W x r + H t − 1 W h r + b r ) , Z t = σ ( X t W x z + H t − 1 W h z + b z ) , \begin{gathered} \mathbf{R}_{t} =\sigma(\mathbf{X}_t\mathbf{W}_{xr}+\mathbf{H}_{t-1}\mathbf{W}_{hr}+\mathbf{b}_r), \\ \mathbf{Z}_t =\sigma(\mathbf{X}_t\mathbf{W}_{xz}+\mathbf{H}_{t-1}\mathbf{W}_{hz}+\mathbf{b}_z), \end{gathered} Rt=σ(XtWxr+Ht−1Whr+br),Zt=σ(XtWxz+Ht−1Whz+bz),
其中,W权重参数,b是偏置参数。
候选隐状态
接下来,重置门 R t \mathbf{R}_{t} Rt就要发挥它的控制作用了。前面我们说到,重置门和更新门都被设计成(0,1)区间的向量。只要将它们和被控制对象做一个简单的乘法(按元素乘),就能发挥它们的控制作用。重置门中的项接近于0表示较多地忽略前一个隐状态的信息,而接近于1表示较多地保留前一个隐状态的信息。然后,我们就可以很容易理解候选隐状态 H ~ t ∈ R n × h \tilde{\mathbf{H}}_t\in\mathbb{R}^{n\times h} H~t∈Rn×h的计算了:
H ~ t = tanh ( X t W x h + ( R t ⊙ H t − 1 ) W h h + b h ) \tilde{\mathbf{H}}_t=\tanh(\mathbf{X}_t\mathbf{W}_{xh}+(\mathbf{R}_t\odot\mathbf{H}_{t-1})\mathbf{W}_{hh}+\mathbf{b}_h) H~t=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh)
其中,W权重参数,b是偏置参数, 符号 ⊙ \odot ⊙是Hadamard积(按元素乘积)运算符。 在这里,我们使用tanh非线性激活函数来确保候选隐状态中的值保持在区间(−1,1)中。
候选隐状态将之前的历史信息和当前时间步的输入进行了结合,GRU的记忆能力就体现在这里。候选隐状态的计算有点类似普通的RNN,只不过多了一个重置门和前一个时间步的隐状态做乘法。当重置门打开时,即重置门为1时,计算候选隐状态的过程就相当于普通的RNN了。有了这个重置门,GRU就可以灵活控制需要保留多少历史信息,不至于像普通RNN那样历史信息过度传递或过度保留,从而避免模型在处理长序列或长期依赖关系时出现梯度消失或梯度爆炸的问题。
下图说明了应用了重置门之后的计算流程。
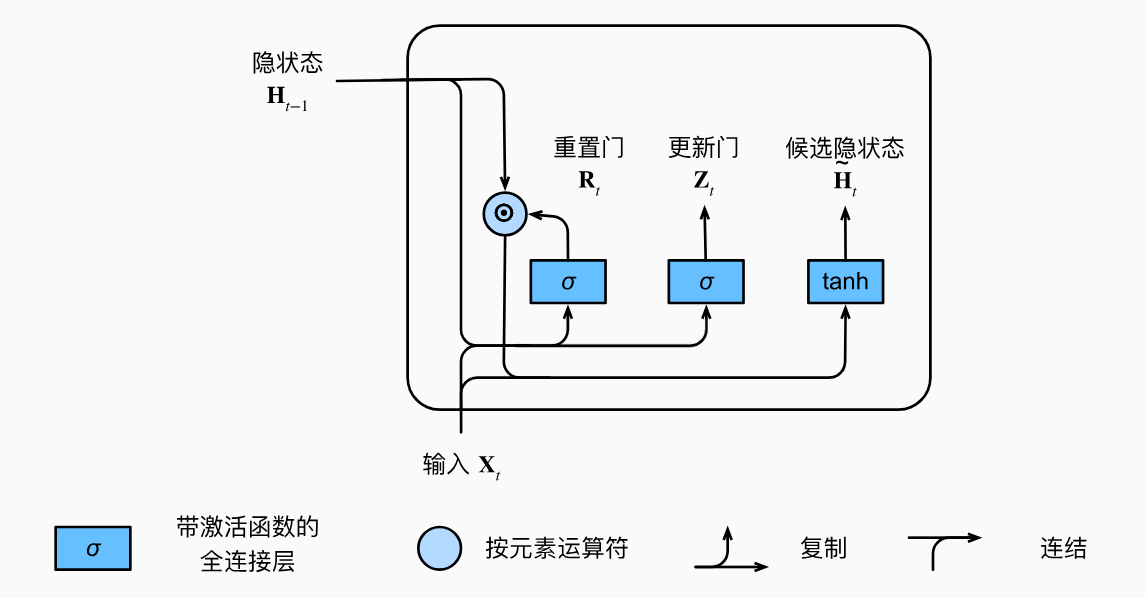
图中,在上一步的基础上,计算出重置门的值后,将其和前一个时间步的隐状态做乘法,然后和当前输入 X t \mathbf{X}_t Xt一起输入进一个带激活函数的全连接层得到候选隐状态。
隐状态
上述的计算结果只是候选隐状态,我们仍然需要结合更新门 Z t \mathbf{Z}_{t} Zt的效果。 这一步确定新的隐状态 H t ∈ R n × h \mathbf{H}_t\in\mathbb{R}^{n\times h} Ht∈Rn×h在多大程度上来自旧的状态 H t − 1 \mathbf{H}_{t-1} Ht−1和新的候选状态 H ~ t \tilde{\mathbf{H}}_t H~t。更新门 Z t \mathbf{Z}_{t} Zt仅需要在 H t − 1 \mathbf{H}_{t-1} Ht−1和 H ~ t \tilde{\mathbf{H}}_t H~t之间进行按元素的凸组合就可以实现这个目标。这就得出了门控循环单元的最终更新公式:
H t = Z t ⊙ H t − 1 + ( 1 − Z t ) ⊙ H ~ t \mathbf{H}_t=\mathbf{Z}_t\odot\mathbf{H}_{t-1}+(1-\mathbf{Z}_t)\odot\mathbf{\tilde{H}}_t Ht=Zt⊙Ht−1+(1−Zt)⊙H~t
每当更新门 Z t \mathbf{Z}_{t} Zt接近1时,模型就倾向只保留旧状态。此时,来自 X t \mathbf{X}_t Xt的信息基本上被忽略,从而有效地跳过了依赖链条中的时间步 t t t。相反,当 Z t \mathbf{Z}_{t} Zt接近0时,新的隐状态 H t \mathbf{H}_t Ht就会接近候选隐状态 H ~ t \tilde{\mathbf{H}}_t H~t。这些设计可以帮助我们处理循环神经网络中的梯度消失问题,并更好地捕获时间步距离很长的序列的依赖关系。例如,如果整个子序列的所有时间步的更新门都接近于1,则无论序列的长度如何,在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。
下图说明了应用了更新门之后的计算流程。
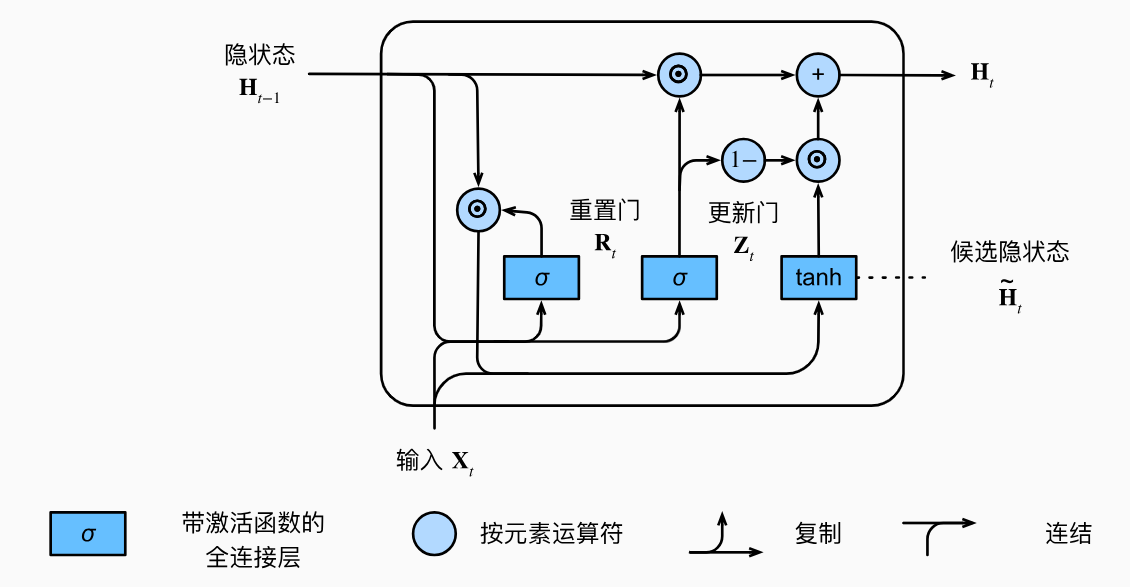
图中,在上一步的基础上,前一个时间步的隐状态和更新门的乘积再加上候选隐状态和 1 − Z t 1-\mathbf{Z}_t 1−Zt的乘积得到当前时间步的隐状态。
总之,门控循环单元具有以下两个显著特征:
- 重置门有助于捕获序列中的短期依赖关系;
- 更新门有助于捕获序列中的长期依赖关系。
最终输出
GRU的最终输出通常与隐状态相关联。可以根据任务的具体要求,将隐状态传递给其他层或将其用作最终输出。例如,在语言模型中,可以将隐状态传递给全连接层进行分类或生成。
总结
- 门控循环神经网络可以更好地捕获时间步距离很长的序列上的依赖关系。
- 重置门有助于捕获序列中的短期依赖关系。
- 更新门有助于捕获序列中的长期依赖关系。
- 重置门打开时,门控循环单元包含基本循环神经网络;更新门打开时,门控循环单元可以跳过子序列。
相关文章:

门控循环单元(GRU)
概述 门控循环单元(Gated Recurrent Unit, GRU)由Junyoung Chung等人于2014年提出,原论文为《Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling》。GRU是循环神经网络(Recurrent Neural Network, …...

789. 数的范围 (二分学习)左端大右,右端小左
题目链接https://www.acwing.com/file_system/file/content/whole/index/content/4317/ 当求左端点时,条件是a【mid】大于等于x,并把右端点缩小。 当求右端点时,条件是a【mid】小于等于x,并把左端点扩大。 1.确定一个区间&…...

docker logs 查找日志常用命令
docker logs 是什么 docker logs 是 Docker 命令行工具提供的一个命令,用于查看容器的日志输出。它可以显示容器在运行过程中生成的标准输出(stdout)和标准错误输出(stderr),帮助用户诊断容器的行为和排查…...

百卓Smart管理平台 importexport.php SQL注入漏洞复现(CVE-2024-27718)
0x01 产品简介 百卓Smart管理平台是北京百卓网络技术有限公司(以下简称百卓网络)的一款安全网关产品,是一家致力于构建下一代安全互联网的高科技企业。 0x02 漏洞概述 百卓Smart管理平台 importexport.php 接口处存在SQL注入漏洞,攻击者除了可以利用 SQL 注入漏洞获取数据…...

PHP教程_PHP5函数str_replace替换字符串中的字符
PHP教程_PHP5函数str_replace替换字符串中的字符 PHP (PHP: Hypertext Preprocessor) 即 “超文本预处理器”, 是在服务器端执行的脚本语言, 尤其适用于Web开发并可嵌入HTML中。 PHP 语法学习了 C语言, 吸纳 Java 和 Perl 多个语言的特色发展出自己的特色语法, 并根据它们的长…...
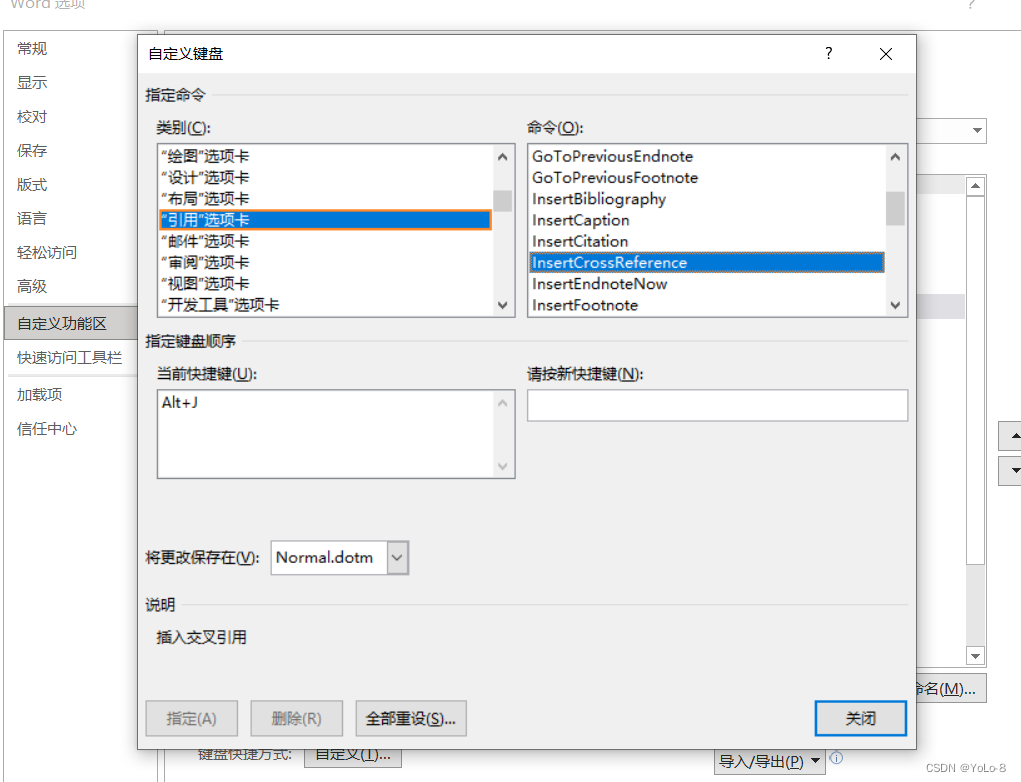
Word的”交叉引用“和”插入题注“快捷键设置
Word的”交叉引用“和”插入题注“快捷键设置 在MSWord2021中,可以自定义设置快捷键。方法如下:文件-选项-自定义功能区-键盘快捷方式(自定义)。具体过程如图所示。 最后,按照上述流程将插入题注(Insert…...
小白从0学习ctf(web安全)
文章目录 前言一、baby lfi(bugku-CTF)1、简介2、解题思路1、解题前置知识点2、漏洞利用 二、baby lfi 2(bugku-CTF)1.解题思路1、漏洞利用 三、lfi(bugku CTF)1、解题思路1、漏洞利用 总结 前言 此文章是…...

【嵌入式开发 Linux 常用命令系列 7.4 -- awk 处理文件名,去除后缀只保留文件名】
请阅读【嵌入式开发学习必备专栏 】 文章目录 awk 处理文件名,去除后缀只保留文件名 awk 处理文件名,去除后缀只保留文件名 在 shell 中, 可以使用 awk 来处理文件名,去除其后缀。下面是一个示例命令,它会将带有后缀的…...

Linux重点思考(中)--端口/静态内存/负载/日志
这里写目录标题 知道的linux常用命令:查看指定端口进程netstat -pantunetstat -pantu|grep 22 静态运行内存free硬盘物理内存df和du当前负载uptime查看日志awk统计文件每一行单词sed 替换文件单词 知道的linux常用命令:查看指定端口进程 netstat -pantu…...
【Go】五、流程控制
文章目录 1、if2、switch3、for4、for range5、break6、continue7、goto8、return 1、if 条件表达式左右的()是建议省略的if后面一定要有空格,和条件表达式分隔开来{ }一定不能省略if后面可以并列的加入变量的定义 if count : 20;count < 30 {fmt.Println(&quo…...

数据开发-面试真题。
1. 自我介绍 2.在培训班的学过的项目经历 3.之前的工作经历,以及薪资 4.开始讲之前的项目经历 5.技术面试官开始提问。 kafka中进行数据分层,怎么从kafka中实时查询到相关的数据,一条或几条 6.java中的集合,以及io流 7.给定…...
如何使用免费的ChatGpt3.5
如何使用免费的ChatGpt 最近免费的gpt3.5很多都不怎么行了实在是太给力了尾声 最近免费的gpt3.5很多都不怎么行了 原因是什么呢?因为openai已经取消了免费的5刀赠送,那么这些人手上的免费的sses-key 用完后,就基本上全军覆没了,再…...

Kafka硬核干货
目录 Kafka Kafka Producer Kafka Consumer Consumer Offset Log Manager 如何实现高吞吐、低延迟...
分享几个可以免费使用的GPT网站吧
1. ChatGAI ChatGAI是一个界面简洁的AI平台,提供App和网页版,每日均有免费使用机会。 2. ChatGPT 本网站向大家开放了ChatGPT 3.5和4.0版本的免费体验,特别适合新用户。每天都有免费次数,响应迅速,注册便捷࿰…...

MySQL进阶-----前缀索引、单例与联合索引
目录 前言 一、前缀索引 1. 语法 2. 如何选择前缀长度 3. 前缀索引的查询流程 二、单列索引与联合索引 三、索引设计原则 前言 本期是MySQL进阶篇当中索引的最后一期内容,这里我们主要接着上一期继续讲解前缀索引、单例与联合索引。(上一期链接&…...
HTTP——Cookie
HTTP——Cookie 什么是Cookie通过Cookie访问网站 我们之前了解了HTTP协议,如果还有小伙伴还不清楚HTTP协议,可以点击这里: https://blog.csdn.net/qq_67693066/article/details/136895597 我们今天来稍微了解一下HTTP里面一个很小的部分&…...

Scala大数据开发
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl Scala简述 在此,简要介绍 Scala 的基本信息和情况。 Scala释义 Scala 源自于英语单词scalable,表示可伸缩的、可扩展的含义。 Scala作者 Scala编…...

windows无法使用hadoop报错:系统找不到路径
在windows下安装hadoop-3.1.4,进行环境变量配置后,打开window命令行窗口测试hadoop命令,报错,如图所示: 方案:由于JAVA_HOME路径有空格导致,可修改hadoop下\etc\hadoop\hadoop_env.cmd文档中set JAVA_HOME以…...
从0配置React
在本地安装和配置React项目,您可以使用create-react-app这个官方推荐的脚手架工具。以下是安装React的步骤,包括安装Node.js、使用create-react-app创建React应用,以及启动开发服务器。 下载安装node.js运行以下命令,验证Node.js…...

File和IO流
1. File类常用方法 1.1 获取基本属性 • public String getName() :获取名称 • public String getPath() :获取路径 • public String getAbsolutePath():获取绝对路径 • public File getAbsoluteFile():获取绝对路径表示…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
