算法沉淀——动态规划篇(子数组系列问题(上))
算法沉淀——动态规划篇(子数组系列问题(上))
- 前言
- 一、最大子数组和
- 二、环形子数组的最大和
- 三、乘积最大子数组
- 四、乘积为正数的最长子数组长度
前言
几乎所有的动态规划问题大致可分为以下5个步骤,后续所有问题分析都将基于此
-
1.、状态表示:通常状态表示分为基本分为以下两种,其中更是以第一种为甚。
以i为结尾,dp[i] 表示什么,通常为代求问题(具体依题目而定)以i为开始,dp[i]表示什么,通常为代求问题(具体依题目而定)
-
2、状态转移方程
*以上述的dp[i]意义为以i位置为分界, 通过最近一步来分析和划分问题,由此来得到一个有关dp[i]的状态转移方程。 -
3、dp表创建,初始化
- 动态规划问题中,如果直接使用状态转移方程通常会伴随着
越界访问等风险,所以一般需要初始化。而初始化最重要的两个注意事项便是:保证后续结果正确,不受初始值影响;下标的映射关系。 - 而
初始化一般分为以下两种:直接初始化开头的几个值。一维空间大小+1,下标从1开始;二维增加一行/一列。
- 动态规划问题中,如果直接使用状态转移方程通常会伴随着
-
4、填dp表、填表顺序:根据状态转移方程来确定填表顺序。
-
5、确定返回值
一、最大子数组和
【题目链接】:53. 最大子数组和
【题目】:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
&emdp;子数组是数组中的一个连续部分。
【示例】:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
【分析】:
我们可以定义dp[i]表示以i为结尾,最大连续子数组和。此时连续子数组长度分为1和大于1,分别对应如下情况:
- 如果dp[i-1]大于0,此时最大连续子数组和为dp[i-1] + nums[i]。长度大于1。
- 如果dp[i-1] <= 0,此时最大的连续子数组和就是nums[i]本身。长度为1.
所以我们可以得到状态转移方程为:dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1])。
但显然当i为0时,状态转移方程不适用。这里我们给出的方法时dp表空间额外增加1。同时为了保证在使用状态转移方程,新增空间对后续填表结果不产生印象。我们将dp[0]初始化为0即可。
【代码编写】:
class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> dp(n + 1);int ret = INT_MIN;for(int i = 1; i <= n; i++){dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);ret = max(ret, dp[i]);}return ret;}
};
二、环形子数组的最大和
【题目链接】:918. 环形子数组的最大和
【题目】:
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
&emsp子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], …, nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
【示例】:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
提示:
n == nums.length
1 <= n <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
【分析】:
显然如果我们"死板"按照题目所说的环形数组进行分析,会感到无从下手。所以我们可以换一种思路:我们对数组被偷元素是否包含首尾,进行分类讨论。从而将环形数组问题转化称求普通子数组的最大和问题!
分类情况:
-
首位元素都被选,此时我们将原问题转化成求普通数组中子数组的最小和。最后用整个数组的和减去最小和,间接求出该情况最大值。
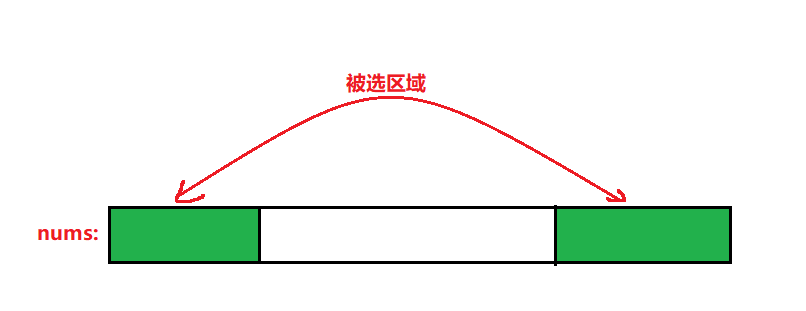
-
首位元素不全都被选。此时原问题转化成普通数组中子数组的最大和。
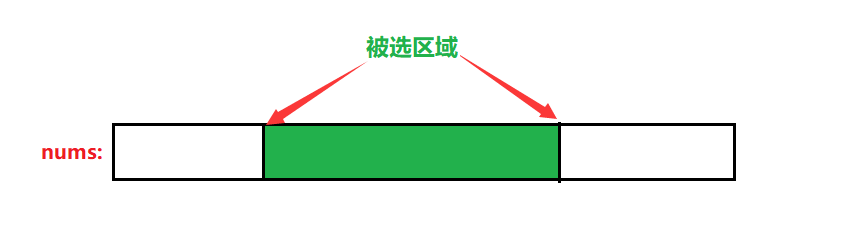
如何求普通数组最大子数组和、最小子数组和:
这里我们可以定义fi]表示以i位置为结尾的子数组最大和,g[i]表示以i位置为结尾的子数组最小和。
状态转移方程推导:
- 以i位置为结尾的子数组最大和分两种情况:如果f[i-1] >0, 此时最大子数组和为f[i-1] + nums[i]。否则最大子数组和为nums[i]本身。所以状态转移方程为:
f[i] = max(nums[i], dp[i-1] + nums[i])。 - 同理,以i位置为结尾的子数组最小和分两种情况:如果f[i-1] <0, 此时最小子数组和为f[i-1] + nums[i]。否则最小子数组和为nums[i]本身。所以状态转移方程为:
g[i] = min(g[i-1]+ nums[i], nums[i])
细节处理:
显然不管是求f[i]还是g[i],当i为0时,状态转移方程失效。这里各位办法是给f、g都额外新增一个空间。最后从左往右依次填表即可。
如果数组中元素全为负数时,此时子数组和最大值一定为负数。但此时我们发现g[i]最终求得的子数组最小和就是整个数组和,此时数组和减子数组最小和的最终结果为0。需要单独处理

【代码编写】:
class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {//数组和int sum = 0;for(auto x : nums){sum += x;}int n = nums.size();vector<int> f(n + 1);//普通数组最大连续子数组和auto g = f;//普通数组最小连续子数组和int fmax = INT_MIN, gmin = INT_MAX;//分别统计f中最大值,g中最小值for(int i = 1; i <= n; i++){f[i] = max(nums[i - 1], f[i - 1] + nums[i - 1]);fmax = max(fmax, f[i]);g[i] = min(nums[i - 1], g[i - 1] + nums[i - 1]);gmin = min(gmin, g[i]);}return sum == gmin ? fmax : max(fmax, sum - gmin);//判断数组元素是否全为负数}
};
三、乘积最大子数组
【题目链接】:152. 乘积最大子数组
【题目】:
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
&emsp测试用例的答案是一个 32-位 整数。
【示例】:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
【分析】:
我们可以定义f[i]表示以i为结尾的最大子数组乘积,g[i]表示以i为结尾的最小子数组乘积。
状态转移方程推导
-
以i为结尾的子数组长度可能为1,或大于1。对于大于1的情况,如果nums[i]>0,此时最大子数组乘积为g[i-1]*nums[i];如果nums[i]<0,此时最大子数组乘积为g[i-1]*nums[i]。我们仅需直接求得3种情况的最大值即可,即状态转移方程为:
f[i] = max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]))。
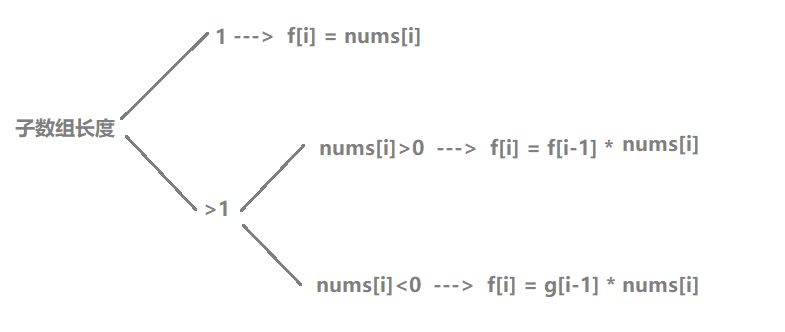
-
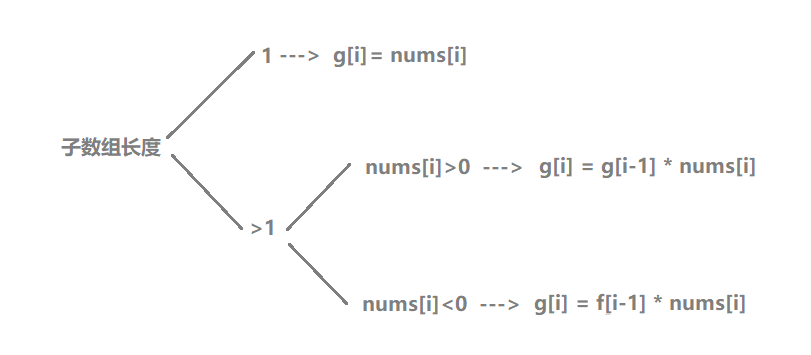
同理对于g[i]来说,也存在如下几种情况。最终可得状态转移方程为
g[i] = min(nums[i - 1], min(g[i - 1] * nums[i - 1], f[i - 1] * nums[i - 1]));
细节处理:
当i=0时,f、g的状态转移方程不适用。我们可以为f、g额外增加1个空间。同时为了防止新增结果对后续填表造成影响,我们将g[0]、f[0]初始化为1。
【代码编写】
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1);//f[i]表示以i为结尾的子数组的最大乘积auto g = f;//g[i]表示以i为结尾的子数组的最小乘积int ret = INT_MIN;f[0] = 1, g[0] = 1;for(int i = 1; i <= n; i++){f[i] = max(nums[i - 1], max(f[i - 1] * nums[i - 1], g[i - 1] * nums[i - 1]));g[i] = min(nums[i - 1], min(g[i - 1] * nums[i - 1], f[i - 1] * nums[i - 1]));ret = max(ret, f[i]);}return ret;}
};
四、乘积为正数的最长子数组长度
【题目链接】:1567. 乘积为正数的最长子数组长度
【题目】:
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
【示例】:
输入:nums = [-1,-2,-3,0,1]
输出:2
解释:乘积为正数的最长子数组是 [-1,-2] 或者 [-2,-3] 。
【分析】:
我们定义f[i]表示以i为结尾,乘积为正的子数组最长长度;g[i]表示以i为结尾,乘积为负的子数组最长长度。
状态转移方程推导:
我们可以从最后一个元素nums[i[入手,此时分为以下几种情况:
- 最长子数组长度可能为1,或大于1,具体如下:
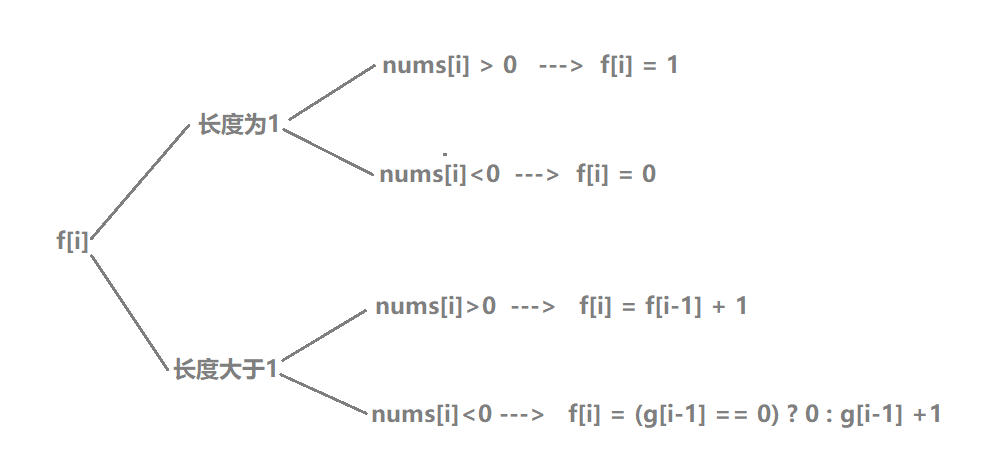
将上述情况仅需合并后,可得:
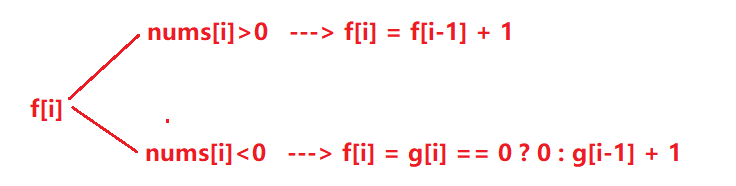
- 同理,g[i]的情况如下:
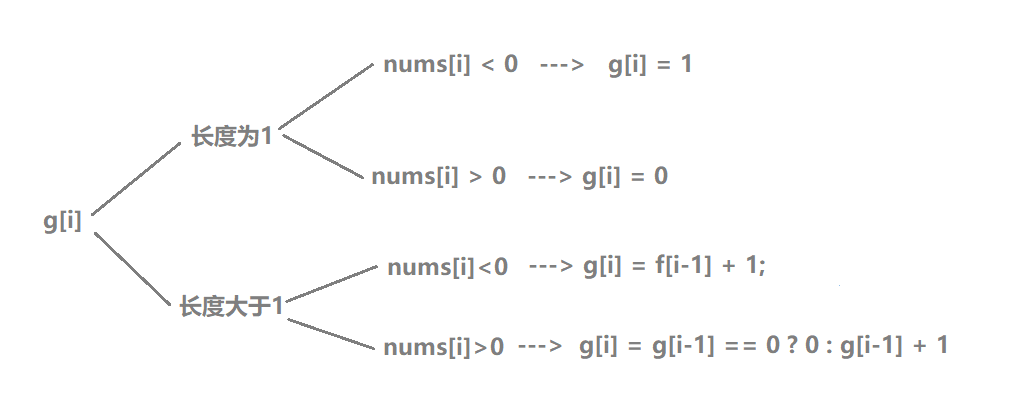
合并后,可得:

细节处理:
显然当i为0时,f、g的状态转移方程都失效。所以我们给f、g额外增加一个空间。为了保证新增空间对后续填表结果不造成印象,我们将f[0]、g[0]初始化为0。最后从左往右填表即可。
【代码编写】:
class Solution {
public:int getMaxLen(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1);//f[i]: 以i为结尾的,乘积为正的最长子数组长度auto g = f;//g[i]: 以i为结尾的,乘积为负的最长子数组长度int ret = INT_MIN;for(int i = 1; i <= n; i++){if(nums[i - 1] > 0){f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;}else if(nums[i - 1] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}ret = max(ret, f[i]);}return ret;}
};
相关文章:

算法沉淀——动态规划篇(子数组系列问题(上))
算法沉淀——动态规划篇(子数组系列问题(上)) 前言一、最大子数组和二、环形子数组的最大和三、乘积最大子数组四、乘积为正数的最长子数组长度 前言 几乎所有的动态规划问题大致可分为以下5个步骤,后续所有问题分析都…...
通知中心架构:打造高效沟通平台,提升信息传递效率
随着信息技术的快速发展,通知中心架构作为一种关键的沟通工具,正逐渐成为各类应用和系统中必不可少的组成部分。本文将深入探讨通知中心架构的意义、设计原则以及在实际场景中的应用。 ### 什么是通知中心架构? 通知中心架构是指通过集中管…...
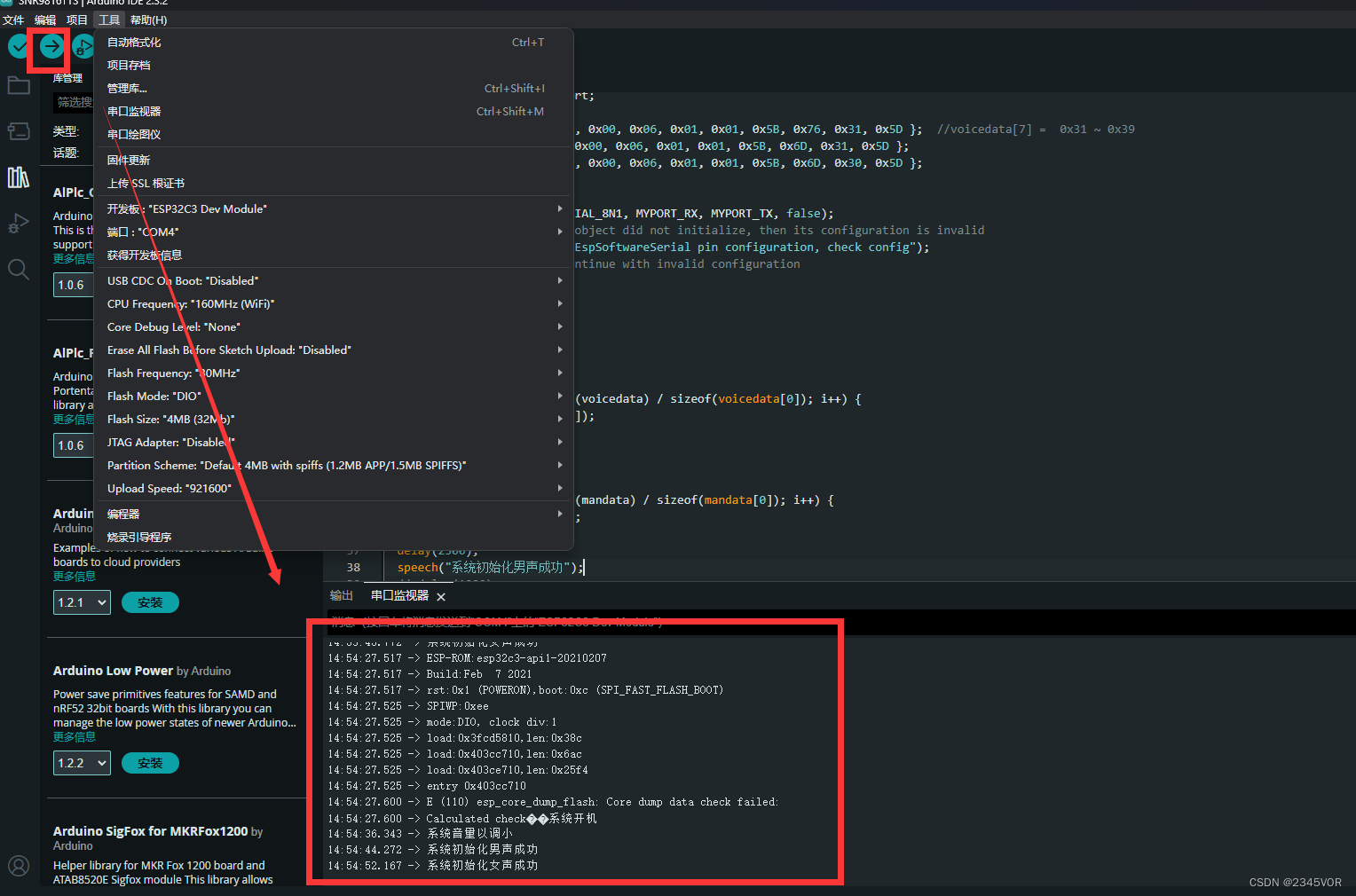
【Arduino使用SNR9816TTS模块教程】
【Arduino使用SNR9816TTS模块教程】 1.前言2. 硬件连接3. Arduino代码3.1 环境配置3.2 Arduino源码 4. 调试步骤5. 总结 1.前言 在今天的教程中,我们将详细介绍如何使用Arduino IDE开发ESP32C3与汕头新纳捷科技有限公司生产的SNR9816TTS中文人声语音合成模块进行交…...
)
牛客练习赛123(A,B,C,D)
牛客挑战赛,练习赛和小白月赛周赛不是一种东西。这玩意跟CF的div12差不多难度。而且找不到题解。所以决定不等题解补题了,直接写题解了。 比赛链接 光速签到下班,rk。感觉E可能能补掉,看情况补吧。 B题感觉之前考了两次&#x…...
docker部署-RabbitMq
1. 参考 RabbitMq官网 docker官网 2. 拉取镜像 这里改为自己需要的版本即可,下面容器也需要同理修改 docker pull rabbitmq:3.12-management3. 运行容器 docker run \ --namemy-rabbitmq-01 \ -p 5672:5672 \ -p 15672:15672 \ -d \ --restart always \ -…...
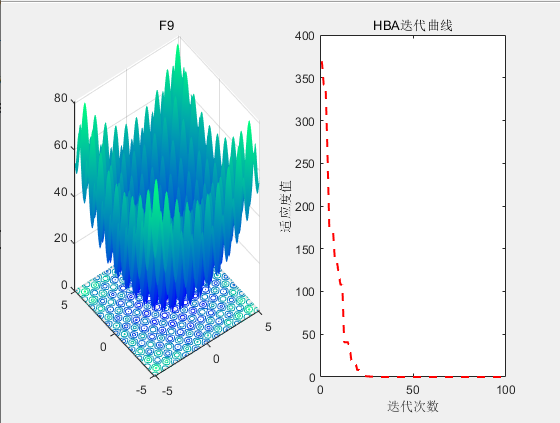
【智能算法】蜜獾算法(HBA)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2021年,FA Hashim等人受到自然界中蜜獾狩猎行为启发,提出了蜜獾算法((Honey Badger Algorithm,HBA)。 2.算法原理 2.1算法思想 蜜獾以其…...
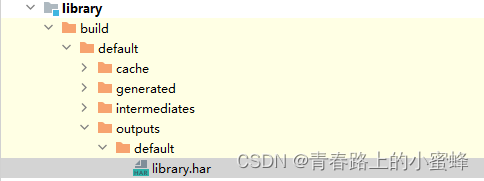
9、鸿蒙学习-开发及引用静态共享包(API 9)
HAR(Harmony Archive)是静态共享包,可以包含代码、C库、资源和配置文件。通过HAR可以实现多个模块或多个工程共享ArkUI组件、资源等相关代码。HAR不同于HAP,不能独立安装运行在设备上,只能作为应用模块的依赖项被引用。…...

[Pytorch]:PyTorch中张量乘法大全
在 PyTorch 中,有多种方法可以执行张量之间的乘法。这里列出了一些常见的乘法操作: 总结: 逐元素乘法:*ortorch.mul()矩阵乘法:ortorch.mm()ortorch.matmul()点积:torch.Tensor.dot()批量矩阵乘法ÿ…...

【软考】防火墙技术
目录 1. 概念2. 包过滤防火墙3. 应用代理网关防火墙4. 状态检测技术防火墙 1. 概念 1.防火墙(Firewall)是建立在内外网络边界上的过滤封锁机制,它认为内部网络是安全和可信赖的,而外部网络是不安全和不可信赖的。2.防火墙的作用是防止不希望的、未经授权…...

OpenHarmony实战:Makefile方式组织编译的库移植
以yxml库为例,其移植过程如下文所示。 源码获取 从仓库获取yxml源码,其目录结构如下表: 表1 源码目录结构 名称描述yxml/bench/benchmark相关代码yxml/test/测试输入输出文件,及测试脚本yxml/Makefile编译组织文件yxml/.gitat…...

嵌入式C语言--GPT通用定时器
嵌入式C语言–GPT通用定时器 嵌入式C语言--GPT通用定时器 嵌入式C语言--GPT通用定时器一. GPT基本概念二. GPT的作用三. GPT通道的四个状态四. Continuous/One-Shot模式3.1)Continuous模式3.2)One-Shot模式 一. GPT基本概念 GPT即General Purpose Timer…...

『Apisix系列』破局传统架构:探索新一代微服务体系下的API管理新范式与最佳实践
一、『Apisix安装部署』 🚀 1.1 手把手教你从零部署APISIX高性能API网关 二、『Apisix入门篇』 🚀 2.1 从零到一掌握Apache APISIX:架构解析与实战指南 三、『Apisix进阶篇』 🚀 3.1 动态负载均衡:APISIX的实战演练…...
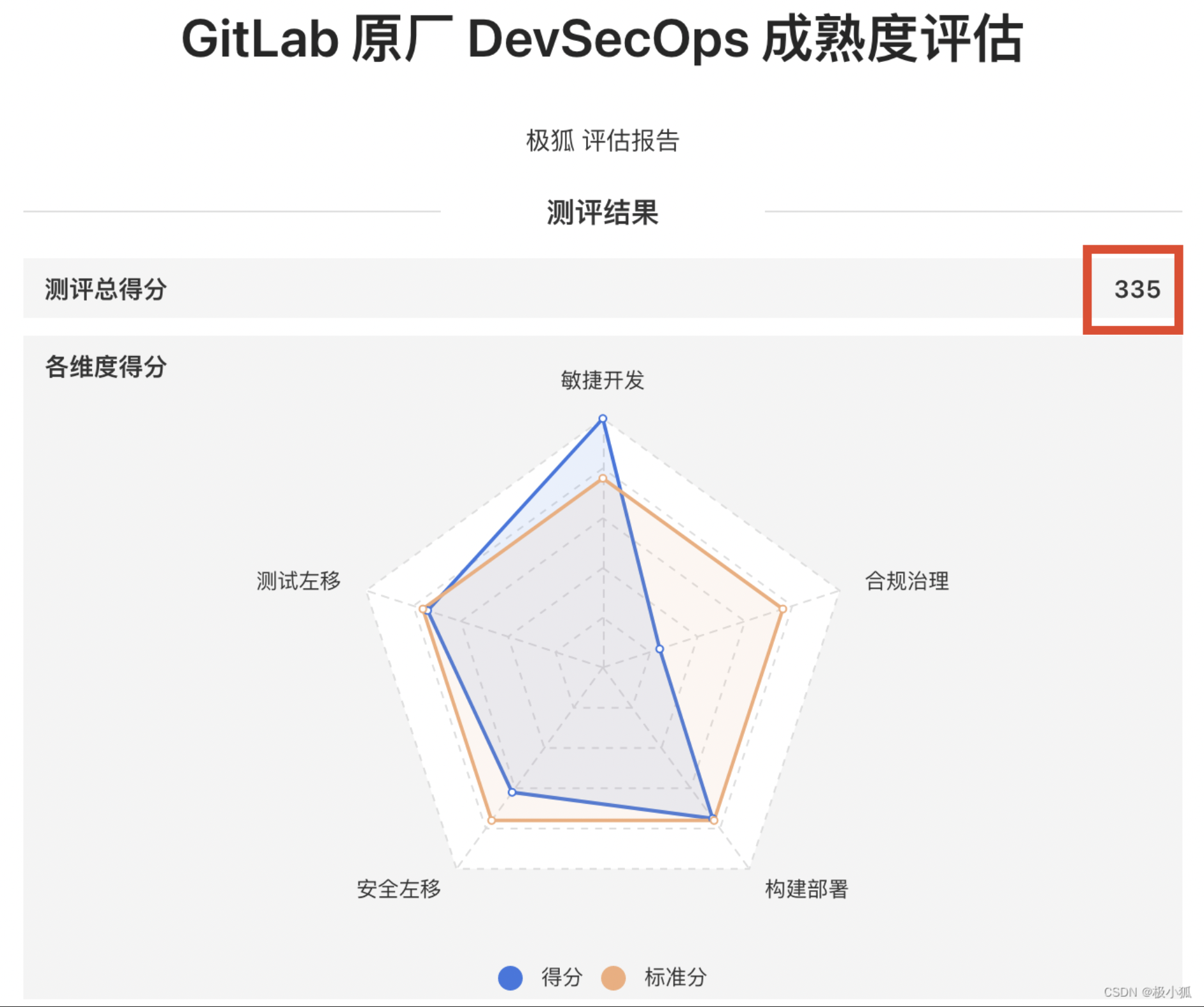
如何在极狐GitLab 自定义 Pages 域名、SSL/TLS 证书
本文作者:徐晓伟 GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 本文主要讲述了在极狐GitLab 用户…...

React Native 应用打包
引言 在将React Native应用上架至App Store时,除了通常的上架流程外,还需考虑一些额外的优化策略。本文将介绍如何通过配置App Transport Security、Release Scheme和启动屏优化技巧来提升React Native应用的上架质量和用户体验。 配置 App Transport…...

单链表就地逆置
算法思想:构建一个带头结点的单链表L,然后访问链表中的每一个数据结点,将访问到的数据结点依此插入到L的头节点之后。 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> typedef int ElemType; typedef s…...
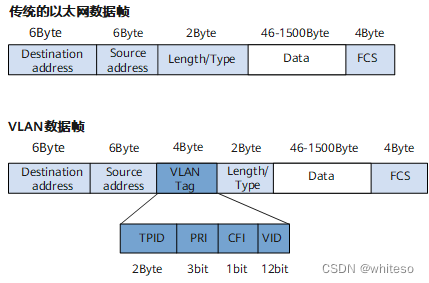
MTU/TCPMSS/VLAN/ACCESS/TRUNK/HYBRID
MTU RFC标准定义以太网的默认MTU值为1500 最小64字节是为了保证最极端的冲突能被检测到,64字节是能被检测到的最小值;最大不超过1518字节是为了防止过长的帧传输时间过长而占用共享链路太长时间导致其他业务阻塞。所以规定以太网帧大小为64~1518字节&am…...

Spring Boot的基础知识和应用
在快速发展的软件开发领域,Spring Boot已经成为了一个广受欢迎的框架,它极大地简化了Spring应用的初始搭建以及开发过程。Spring Boot遵循“约定优于配置”的原则,通过默认配置减少了开发者的配置工作量,使得开发者能够更专注于业…...

【Linux】详解动静态库的制作和使用动静态库在系统中的配置步骤
一、库的作用 1、提高开发效率,让开发者所有的函数实现不用从零开始。 2、隐藏源代码。 库其实就是所有的.o文件用特定的方式进行打包形成一个文件,各个.o文件包含了源代码中的机器语言指令。 二、动态库和静态库的制作和使用 2.1、静态库的制作和使用…...
)
开源模型应用落地-qwen1.5-7b-chat-LoRA微调(二)
一、前言 预训练模型提供的是通用能力,对于某些特定领域的问题可能不够擅长,通过微调可以让模型更适应这些特定领域的需求,让它更擅长解决具体的问题。 本篇是开源模型应用落地-qwen-7b-chat-LoRA微调(一)进阶篇,学习通义千问最新1.5系列模型的微调方式。 二、术语介绍 …...

【现代企业管理】企业组织结构和组织文化的理论与实践——以华为为例
一、前言 管理是科学和艺术的统一体,它是企业成长的保证。企业管理中,管理者面对的往往不是一个完整的系统,而是各种不具有整体规律性的零碎信息的总和,因此进行信息的整合和研究是管理的重点和关键。 组织管理作为管理的四大职…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
