第十三届蓝桥杯大赛软件赛省赛CC++大学B组
第十三届蓝桥杯大赛软件赛省赛CC++ 大学 B 组
文章目录
- 第十三届蓝桥杯大赛软件赛省赛CC++ 大学 B 组
- 1、九进制转十进制
- 2、顺子日期
- 3、刷题统计
- 4、修建灌木
- 5、x进制减法
- 6、统计子矩阵
- 7、积木画
- 8、扫雷
- 9、李白打酒加强版
- 10、砍竹子
1、九进制转十进制

计算器计算即可。2999+29+2。
2、顺子日期

简单的枚举一下2022年的日期即可,注意遇到20220123,判断为一个即可。
#include<iostream>#define ll long long
using namespace std;
int ans=0;
int d[]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);for(int i=1;i<=12;i++){for(int j=1;j<=d[i];j++){int date[]={2,i/10,i%10,j/10,j%10};for(int k=0;k<3;k++){if(date[k]+1==date[k+1]&&date[k+1]+1==date[k+2]){ans++;break;}}}}cout<<ans;return 0;
}
3、刷题统计

分析:
这一题我本来用的是cmath里的ceil函数,但是提交之后我发现只能过掉70%,并没有全部通过。
随后我手写了ceil函数的功能,然后就可以100%通过了。
后来我就发现ceil函数原型是float ceilf (float x); 题意是1e18,肯定就会出现精度问题了,真的要记住这问题了,遇到特大数尽量手心函数,不要用库函数,可能就会出现问题。
#include<iostream>
#include<cmath>
#define ll long long
using namespace std;
ll a,b,n;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>a>>b>>n;ll x=(5*a+2*b);ll y=(n/x);// 坐满了几周,7*y ll z=(n%x);// 还剩的题数 if(z<=5*a){if(z%a==0){z=z/a;}else{z=z/a+1;}cout<<7*y+z;}else{if((z-5*a)%b==0){z=(z-5*a)/b;}else{z=(z-5*a)/b+1;}cout<<7*y+5+z;}return 0;
}
4、修建灌木



这一题直接暴力模拟过程即可,对于案例n=3,我们模拟过程会发现一个规律,那就是在1~n中最高的树是对称的而且最高的树的值都是这两个对称位置步长的2倍。
#include<iostream>
#define ll long long
using namespace std;
int n;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;/*n=3未剪 修剪后 位置111 -> 011 1122 -> 101 2212 -> 210 3321 -> 301 2412 -> 012 1123 -> 103 2214 -> 210 3 可以看到出现了循环情况,也就说从左向右和从右向左,的最大值是就是步长的2倍 */for(int i=1;i<=n;i++){cout<<max(i-1,n-i)*2<<"\n";}return 0;
}
5、x进制减法



没想到啊,感觉脑袋被踢了。
代码示例:
#include<iostream>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
const ll mod = 1000000007,N = 1e5+10;
ll n,ma,mb,a[N],b[N],p[N];
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;// 从高位县向低位输入,避免造成位数不相同 cin>>ma;for(ll i=ma;i>=1;i--)cin>>a[i];cin>>mb;for(ll i=mb;i>=1;i--)cin>>b[i];/*x进制类比一下 十进制 比如 123 就是 1*10*10+2*10+3那么x进制的:每一位的进制:11 5 2每一位的数字:10 4 1那么这个x进制对应的十进制不就是:10*5*2+4*2+1 */// A >= B // 进制: 11 5 2 // 10 4 0 10*5*2+4*2+0=108// 1 2 0 1*5*2+2*2+0=14 108-14=94// 所以说最小的数位上的进制应该就是a[i]和b[i]这个数位的值+1 // 也就是说正好要进位的时候能得到最小值// 我们就使用p[i]来储存每个位上应该是什么进制 for(ll i=1;i<=ma;i++){p[i]=max((ll)2,max(a[i],b[i])+1);}p[0]=1;ll ans=0;for(int i=ma;i>=1;i--){ ans=(ans+a[i]-b[i])*p[i-1]%mod;}cout<<ans;return 0;
}
6、统计子矩阵


分析:
我直接想到的就是二维前缀和解决这个问题,去拿区间的值和k判断即可。
写的时候运行的结果一直不对,后来才发现是公式记错了,所以说记公式很重要。
区间的形式求值得公式是:res=prefix[x2][y2]-prefix[x2][y1-1]-prefix[x1-1][y2]+prefix[x1-1][y1-1] 。
但是直接暴力解决的话,只能过70%,其它的超时。优化的方法自行搜索。
#include<iostream>
#include<cstring>
#define ll long long
#define pii pair<ll,ll>
using namespace std;
const int N = 5e2+10;
ll n,m,k,mp[N][N],prefix[N][N],ans=0;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>k;memset(prefix,0,sizeof(prefix));memset(mp,0,sizeof(mp));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){ cin>>mp[i][j];prefix[i][j]=prefix[i-1][j]+prefix[i][j-1]+mp[i][j]-prefix[i-1][j-1];}for(int x1=1;x1<=n;x1++){for(int y1=1;y1<=m;y1++){for(int x2=x1;x2<=n;x2++){for(int y2=y1;y2<=m;y2++){// s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]ll res=prefix[x2][y2]-prefix[x2][y1-1]-prefix[x1-1][y2]+prefix[x1-1][y1-1];if(res<=k)ans++;}} }} cout<<ans;return 0;
}
7、积木画
8、扫雷


简单的枚举判断一下就行了。
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int N = 105;
int n,m;
int mp[N][N],ans[N][N];
int dx[]={0,0,1,-1,1,-1,1,-1};
int dy[]={1,-1,0,0,1,-1,-1,1};
bool isnmp(int x,int y){return x<0||x>=n||y<0||y>=m;
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=0;i<n;i++)for(int j=0;j<m;j++)cin>>mp[i][j];memset(ans,'0',sizeof(ans));for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(mp[i][j]==1){ans[i][j]=9; }else{int rs=0;for(int k=0;k<8;k++){int nx=i+dx[k],ny=j+dy[k];if(isnmp(nx,ny))continue;if(mp[nx][ny]==1){rs++;}}ans[i][j]=rs;}}} for(int i=0;i<n;i++){for(int j=0;j<m;j++)cout<<ans[i][j]<<" ";cout<<"\n";}return 0;
}
9、李白打酒加强版
10、砍竹子
相关文章:

第十三届蓝桥杯大赛软件赛省赛CC++大学B组
第十三届蓝桥杯大赛软件赛省赛CC 大学 B 组 文章目录 第十三届蓝桥杯大赛软件赛省赛CC 大学 B 组1、九进制转十进制2、顺子日期3、刷题统计4、修建灌木5、x进制减法6、统计子矩阵7、积木画8、扫雷9、李白打酒加强版10、砍竹子 1、九进制转十进制 计算器计算即可。2999292。 2、…...
zookeeper监听集群节点的实现zkclient组件实现方案(Java版)
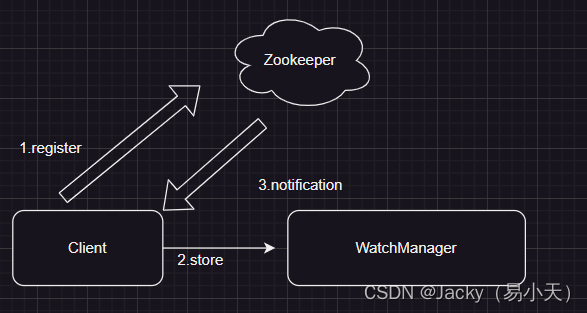
ZooKeeper Watcher 机制 client 向zookeeper 注册监听client注册的同时会存储一个WatchManager对象向zookeeper发生改变则notification client 并发送一个WatchManager对象,然后client再更新该对象 package com.jacky.zk.demo;import org.I0Itec.zkclient.IZkChildListener;…...
【ArduinoQuartus】在小脚丫STEP CYC10上安装PulseRain Reindeer并在软核上运行基础功能
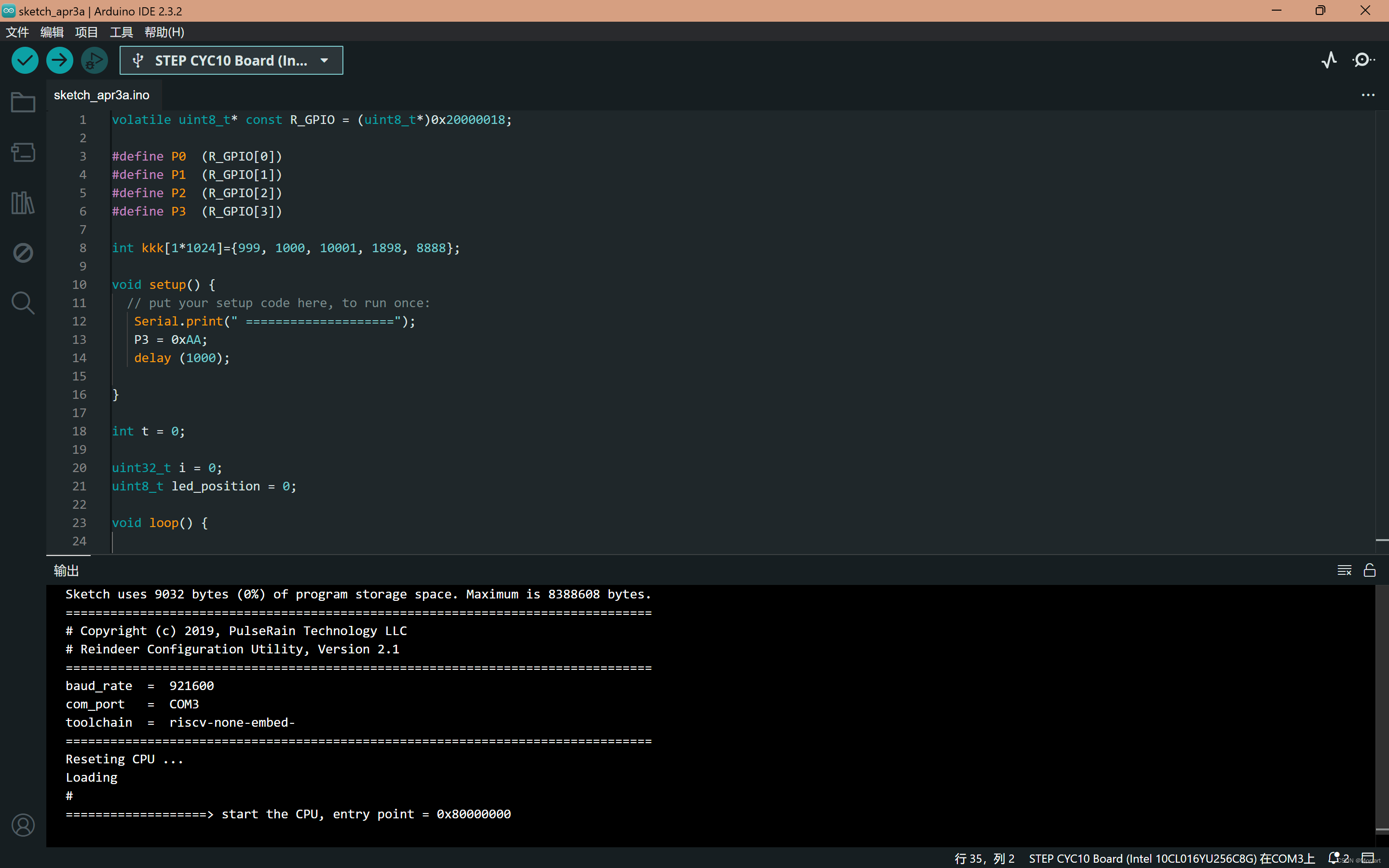
【Arduino&Quartus】在小脚丫STEP CYC10上安装PulseRain Reindeer并在软核上运行基础功能 一、将Reindeer软核下载到STEP CYC10(一)下载PulseRain Reindeer软核(二)配置Reindeer软核到开发板1.将sof文件转换为jic文件2.将jic文…...

【电路笔记】-逻辑与门
逻辑与门 文章目录 逻辑与门1、概述2、2 输入晶体管与门3、数字与门类型4、7408 四路 2 输入与门逻辑与门是一种数字逻辑电路,仅当其所有输入均为高电平时,其输出才会变为高电平至逻辑电平 1。 1、概述 数字逻辑与门的输出状态仅在其任何输入处于逻辑电平“0”时再次返回“低…...

蓝桥杯练习——拼出一个未来
选中 index.html 右键启动 Web Server 服务(Open with Live Server),让项目运行起来。接着,打开环境右侧的【Web 服务】,就可以在浏览器中看到如下效果: 目标 完善 js/index.js 的 TODO 部分,实…...
stm32f103c8t6学习笔记(学习B站up江科大自化协)-SPI
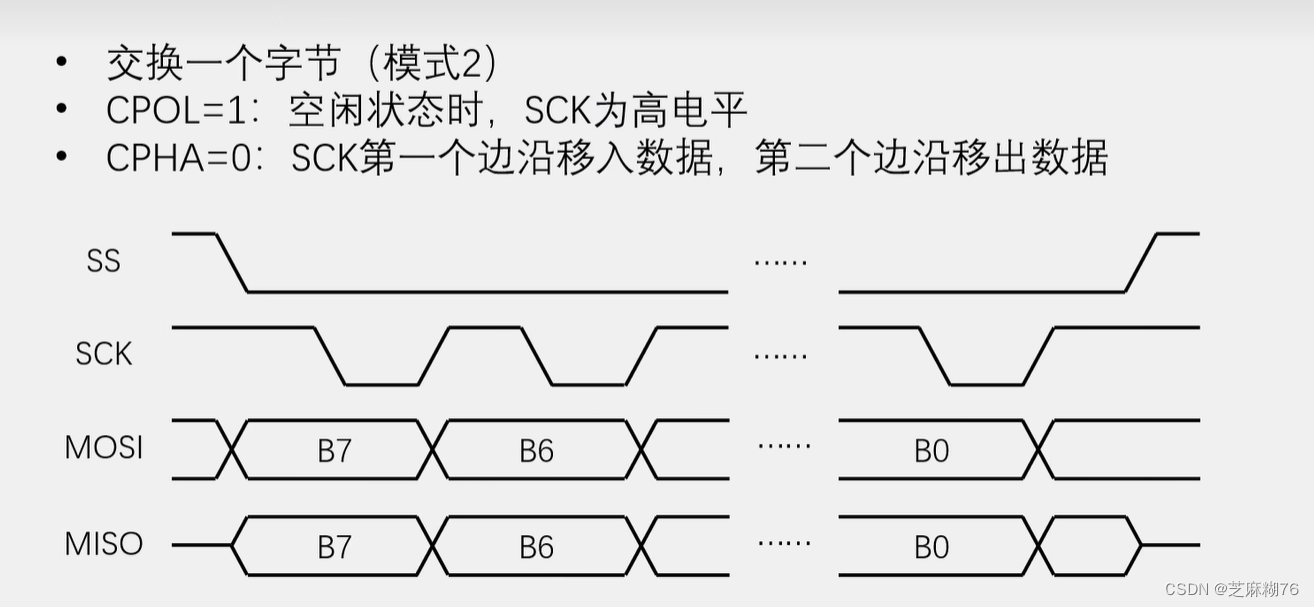
SPI通信 SPI,(serial peripheral interface),字面翻译是串行外设接口,是一种通用的数据总线,适用于主控和外挂芯片之间的通信,与IIC应用领域非常相似。 IIC无论是在硬件电路还是在软件时序设计…...

云计算的安全需求
目录 一、概述 二、云安全服务基本能力要求 三、信息安全服务(云计算安全类)资质要求 3.1 概述 3.2 资质要求内容 3.2.1 组织与管理要求 3.2.2 技术能力要求 四、云安全主要合规要求 4.1 安全管理机构部门的建立 4.2 安全管理规范计划的编制 4…...

【C++】编程规范之表达式原则
表达式中变量的位置 在编写表达式时,将变量放置在右边,可以提高代码的可读性和可理解性。这种做法符合自然语言的阅读习惯,使得代码更易于理解。 // Good if (5 x) {// do something }// Avoid if (x 5) {// do something }不变量和资源申…...

Python人工智能基础知识:理解神经网络与机器学习的基本概念
人工智能(Artificial Intelligence,AI)是当今科技领域的热门话题之一,而神经网络和机器学习作为AI的两个重要分支,在解决各种问题中发挥着重要作用。本文将详细介绍神经网络和机器学习的基本概念,帮助读者更…...
10_MVC
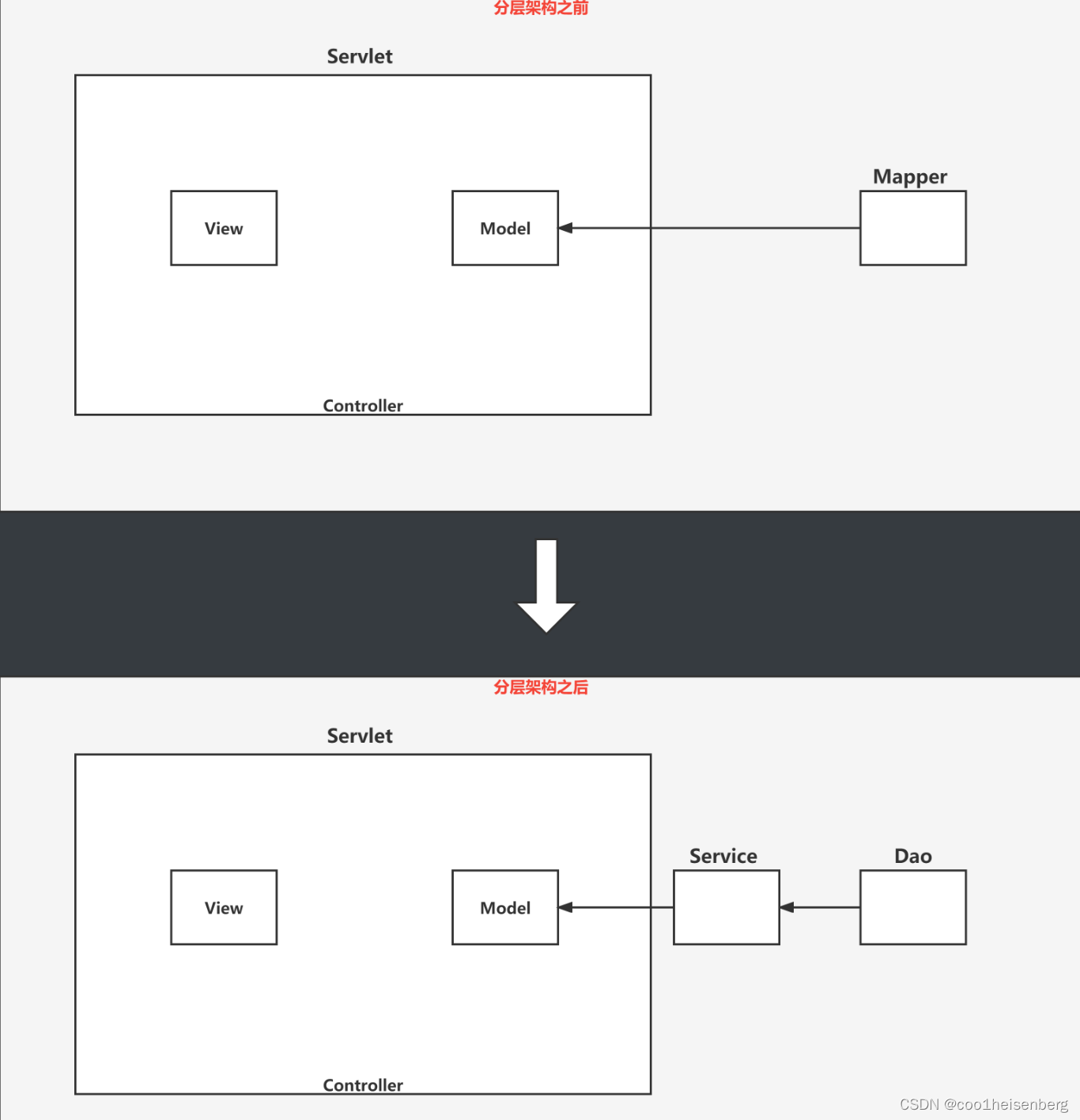
文章目录 JSON常用的JSON解析Jackson的常规使用指定日期格式 MVC设计模式MVC介绍前后端分离案例(开发与Json相关接口) 三层架构三层架构介绍 JSON JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式,是存…...

【Java多线程(4)】案例:设计模式
目录 一、什么是设计模式? 二、单例模式 1. 饿汉模式 2. 懒汉模式 懒汉模式-第一次改进 懒汉模式-第二次改进 懒汉模式-第三次改进 一、什么是设计模式? 设计模式是针对软件设计中常见问题的通用解决方案。它们提供了一种被广泛接受的方法来解决…...

时序预测 | Matlab实现CPO-BiLSTM【24年新算法】冠豪猪优化双向长短期记忆神经网络时间序列预测
时序预测 | Matlab实现CPO-BiLSTM【24年新算法】冠豪猪优化双向长短期记忆神经网络时间序列预测 目录 时序预测 | Matlab实现CPO-BiLSTM【24年新算法】冠豪猪优化双向长短期记忆神经网络时间序列预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现CPO-BiLST…...
|Spring和Spring Boot之间有什么关联和区别)
java面试题(4)|Spring和Spring Boot之间有什么关联和区别
文章目录 Spring和Spring Boot的有什么关联?Spring和Spring Boot有什么区别?如何快速区分某个项目采用的是 Spring 还是 Spring Boot? Spring和Spring Boot的有什么关联? Spring Boot是建立在Spring框架之上的,因此它…...
Spring Boot中前端通过请求接口下载后端存放的Excel模板
导出工具类 package com.yutu.garden.utils;import com.baomidou.mybatisplus.core.toolkit.ObjectUtils; import org.apache.commons.io.IOUtils; import org.apache.poi.hssf.util.HSSFColor; import org.apache.poi.xssf.usermodel.XSSFWorkbook; import org.slf4j.Logger;…...
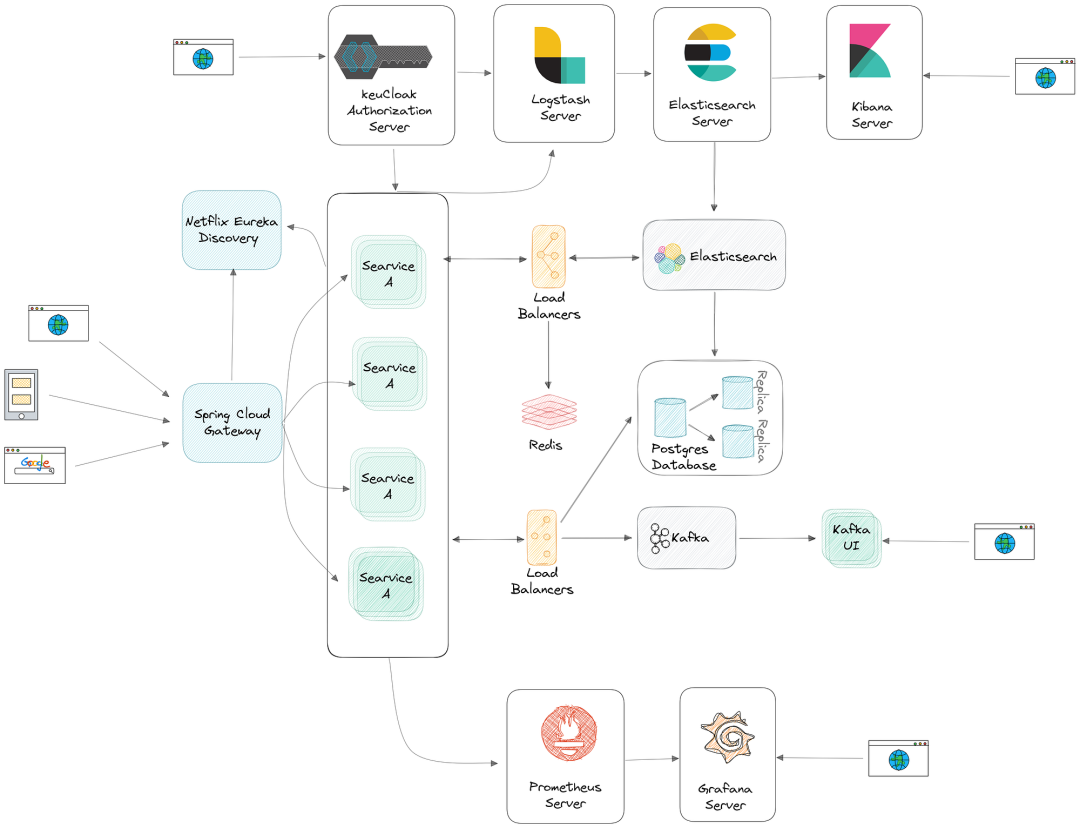
构建企业级微服务平台:实现可扩展性、弹性和高效性
在软件开发的快速发展领域中,企业不断努力构建健壮、可扩展和高效的系统。随着微服务架构的出现,再加上云原生技术的应用,创建敏捷且具有弹性的平台的可能性是无限的。在本指南中,我们将深入探讨使用强大的工具和技术组合…...

存内计算技术在边缘计算、物联网设备中的应用及前景
存内计算技术简介 存内计算技术是一种新兴的计算范式,其核心理念是将存储和计算功能集成在同一硬件单元中。这种技术的优势在于能够在存储单元内部直接进行计算操作,从而减少数据在存储器和处理器之间的传输,提高计算效率。 以下是存内计算技…...

C#使用Selenium驱动Chrome浏览器
1.Selenium库依赖安装 Selenium WebDriver是Selenium项目的一部分,用于模拟用户在Web应用程序中的交互操作。它支持多种浏览器,如Chrome、Firefox、IE等,且与各种编程语言(如Java、Python、C#等)兼容,具有…...
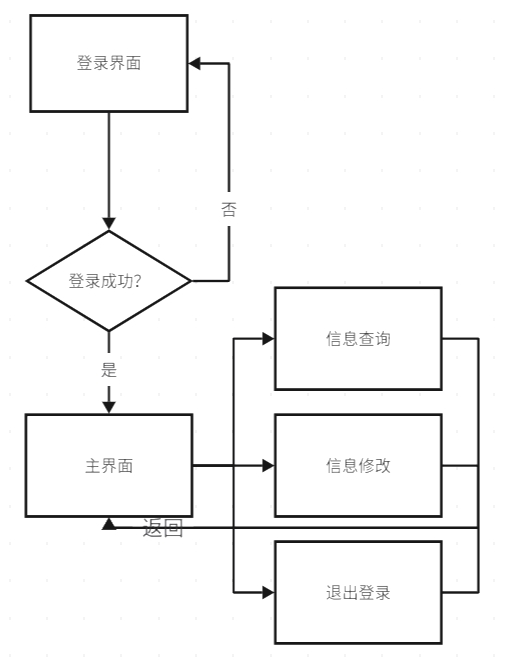
【软件工程】详细设计(二)
这里是详细设计文档的第二部分。前一部分点这里 4. 学生端模块详细设计 学生端模块主要由几个组件构成:学生登录界面,成绩查询界面等界面。因为学生端的功能相对来说比较单一,因此这里只给出两个最重要的功能。 图4.1 学生端模块流程图 4.…...

数据质量决定大模型能力,景联文科技提供高质量大模型数据
随着大模型的深入发展,各类资源要素的配置状态已悄然变化。其中,数据的价值已被提升到一个新高度。 大模型往往拥有庞大的参数和复杂的网络结构,需要大量的数据来学习和优化。数据的质量和数量直接决定了模型的训练效果。若数据不足或质量不佳…...

大话设计模式之状态模式
状态模式是一种行为设计模式,它允许对象在其内部状态发生变化时改变其行为。在状态模式中,对象将其行为委托给当前状态对象,从而在不同的状态下执行不同的行为,而不必在对象自身的代码中包含大量的条件语句。 通常,状…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
