力扣经典150题第一题:合并两个有序数组
目录
- 合并两个有序数组问题详解与解决方法
- 1. 介绍
- 2. 问题描述
- 3. 解题思路
- 4. 算法实现
- 5. 复杂度分析
- 6. 测试和验证
- 7. 扩展
- 如何处理特殊情况和边界条件?
- 如何处理数组中可能存在的重复元素?
- 如何优化算法以减少内存使用或提高执行效率?
- 8. 总结
- 9. 参考文献
合并两个有序数组问题详解与解决方法
1. 介绍
在编程面试中,合并两个有序数组是一个经典的问题。它要求将两个有序数组合并为一个新的有序数组。本篇博客将深入讨论这个问题,并提供解决方法。
2. 问题描述
- 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length ==m+n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
3. 解题思路
合并两个有序数组的一种简单方法是先将两个数组合并,然后进行排序。但这种方法的时间复杂度为 O((m+n)log(m+n)),不够高效。我们可以采用双指针法来解决这个问题,时间复杂度为 O(m+n)。
4. 算法实现
public class MergeSortedArray {public void merge(int[] nums1, int m, int[] nums2, int n) {int index1 = m - 1, index2 = n - 1, indexMerge = m + n - 1;while (index1 >= 0 || index2 >= 0) {if (index1 < 0) {nums1[indexMerge--] = nums2[index2--];} else if (index2 < 0) {nums1[indexMerge--] = nums1[index1--];} else if (nums1[index1] > nums2[index2]) {nums1[indexMerge--] = nums1[index1--];} else {nums1[indexMerge--] = nums2[index2--];}}}
}
5. 复杂度分析
- 时间复杂度:O(m+n),其中 m 和 n 分别为两个数组的长度。
- 空间复杂度:O(1),没有使用额外的空间。
6. 测试和验证
public class Main {public static void main(String[] args) {MergeSortedArray solution = new MergeSortedArray();int[] nums1 = {1, 2, 3, 0, 0, 0};int[] nums2 = {2, 5, 6};int m = 3, n = 3;solution.merge(nums1, m, nums2, n);System.out.println(Arrays.toString(nums1)); // [1, 2, 2, 3, 5, 6]}
}
7. 扩展
- 如何处理特殊情况和边界条件?
- 如何处理数组中可能存在的重复元素?
- 如何优化算法以减少内存使用或提高执行效率?
如何处理特殊情况和边界条件?
- 空数组处理: 需要考虑到两个数组中可能有一个或两个为空的情况,此时不需要进行合并操作,直接返回另一个数组即可。
- 数组长度不足处理: 如果数组长度不足以容纳合并后的所有元素,需要提前扩展数组的长度。
如何处理数组中可能存在的重复元素?
- 跳过重复元素: 在合并过程中,如果遇到重复的元素,可以根据需要选择跳过还是保留重复的元素。
如何优化算法以减少内存使用或提高执行效率?
- 使用辅助数组: 可以使用额外的数组来保存合并后的结果,然后再将结果拷贝回原数组。这样做的好处是可以避免在原数组上频繁操作,从而提高执行效率。
- 空间复杂度优化: 如果原数组
nums1的空间足够大,可以直接在原数组上进行合并操作,而不需要额外的空间。这样可以节省内存使用,但要注意原数组的长度问题。 - 时间复杂度优化: 如果两个数组长度差异较大,可以先判断两个数组中是否有一个为空或者其中一个数组的最后一个元素小于另一个数组的第一个元素,这种情况下不需要进行合并操作,直接返回即可,从而减少不必要的比较和移动操作,优化算法的执行效率。
通过对这些扩展问题的思考和解决,可以进一步完善合并两个有序数组的算法,使之更加健壮和高效。
8. 总结
本篇博客详细介绍了合并两个有序数组的问题,提供了双指针法的解决方法,并给出了Java代码实现。通过对算法的分析和测试验证,我们可以清晰地理解这个问题及其解决方法,希望对读者有所帮助。
9. 参考文献
- LeetCode官方网站
- 《算法导论》
- 《程序员面试金典》
通过这样的完整结构,读者可以全面了解合并两个有序数组的问题,掌握解决方法,并进一步深入学习和探索相关知识。
相关文章:

力扣经典150题第一题:合并两个有序数组
目录 合并两个有序数组问题详解与解决方法1. 介绍2. 问题描述3. 解题思路4. 算法实现5. 复杂度分析6. 测试和验证7. 扩展如何处理特殊情况和边界条件?如何处理数组中可能存在的重复元素?如何优化算法以减少内存使用或提高执行效率? 8. 总结9.…...
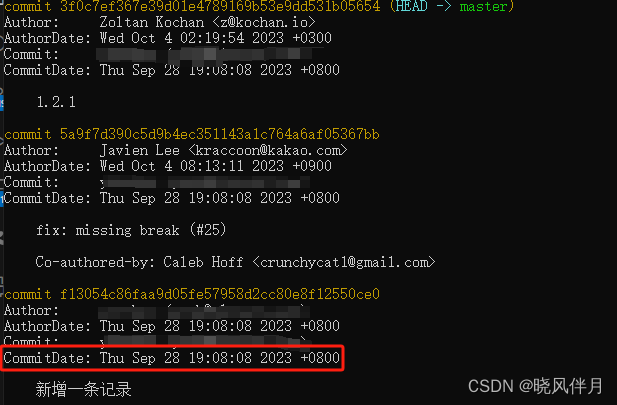
Git:日志修改
一、问题描述 有小伙伴提出一个需求,为了满足某种需要,需要在Git日志中增加一条提交记录,并且需要指定提交时间。 比如,以下面这个only-allow项目为例,想在它的Git日志2023/9/26 19:08:08前插入一条2023/9/28 19:08:0…...
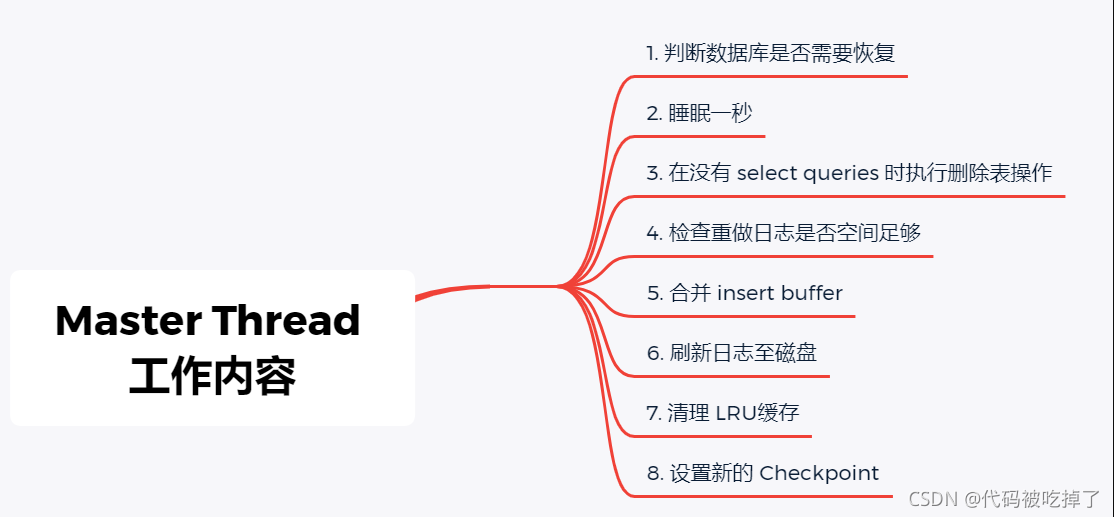
【数据库】MySQL InnoDB存储引擎详解 - 读书笔记
MySQL InnoDB存储引擎详解 - 读书笔记 InnoDB 存储引擎概述InnoDB 存储引擎的版本InnoDB 体系架构内存缓冲池LRU List、Free List 和 Flush List重做日志缓冲(redo log buffer)额外的内存池 存储结构表空间系统表空间独立表空间通用表空间undo表空间临时…...

GPT-2原理-Language Models are Unsupervised Multitask Learners
文章目录 前言GPT-1优缺点回顾GPT-1实验结果分析GPT-1缺陷分析 GPT-2训练数据OpenAI的野心预训练/微调的训练范式训练数据选择 模型结构和参数(更大的GPT-1)模型预训练训练参数 输入数据编码 总结 前言 首先强调一下,在看这篇文章之前&#…...

逆向案例十二——看准网企业信息json格式的信息
网址:【全国公司排行|排名榜单|哪家好】-看准网 打开开发者工具——刷新——网络——XHR——下滑页面加载新的页面——找到数据包 发现参数加密,返回的数据也进行了加密 按关键字在下方搜索 kiv进入第一个js文件 ctrlf打开文件里面的搜索框继续搜kiv找到…...
docker安装jenkins 2024版
docker 指令安装安装 docker run -d --restartalways \ --name jenkins -uroot -p 10340:8080 \ -p 10341:50000 \ -v /home/docker/jenkins:/var/jenkins_home \ -v /var/run/docker.sock:/var/run/docker.sock \ -v /usr/bin/docker:/usr/bin/docker jenkins/jenkins:lts访问…...

输入url到页面显示过程的优化
浏览器架构 线程:操作系统能够进行运算调度的最小单位。 进程:操作系统最核心的就是进程,他是操作系统进行资源分配和调度的基本单位。 一个进程就是一个程序的运行实例。启动一个程序的时候,操作系统会为该程序创建一块内存&a…...
部署hive)
Linux(centos7)部署hive
前提环境: 已部署完hadoop(HDFS 、MapReduce 、YARN) 1、安装元数据服务MySQL 切换root用户 # 更新密钥 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysqL-2022 # 安装Mysql yum库 rpm -Uvh http://repo.mysql.com//mysql57-community-release-el7-7.noarch.rpm # yu…...

LeetCode | 数组 | 双指针法 | 27. 移除元素【C++】
题目链接 1. 题目描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑…...

【Apache Doris】周FAQ集锦:第 2 期
【Apache Doris】周FAQ集锦:第 2 期 SQL问题数据操作问题运维常见问题其它问题关于社区 欢迎查阅本周的 Apache Doris 社区 FAQ 栏目! 在这个栏目中,每周将筛选社区反馈的热门问题和话题,重点回答并进行深入探讨。旨在为广大用户和…...

jQuery(二)
文章目录 1.jQuery操作节点1.查找节点,修改属性1.基本介绍2.切换图片案例 2.创建节点1.基本介绍2.内部插入3.外部插入4.小结1.插入方法说明2.两种插入方法的区别 5.插入元素实例6.移动元素实例 3.删除节点1.基本介绍2.代码实例 4.复制节点1.基本介绍2.代码实例 5.替…...

MIT6.828 实验环境安装教程
Thanks:mit6.828环境搭建 - 人云我不亦云的文章 - 知乎 https://zhuanlan.zhihu.com/p/489921553 sudo make && make install install -d -m 0755 "/share/qemu" install: 无法创建目录 “/share”: 权限不够 make: *** [Makefile:382:…...

一文彻底搞清 Iterator(遍历器)概念及用法
目录 一、由来及意义 二、具体实现流程 三、具有默认 Iterator 接口的数据结构 四、调用 Iterator 接口的场合 五、总结 一、由来及意义 Javascript中表示“集合”的数据结构,主要是 Array、Object、Map、Set 这四种数据集合,除此之外,…...
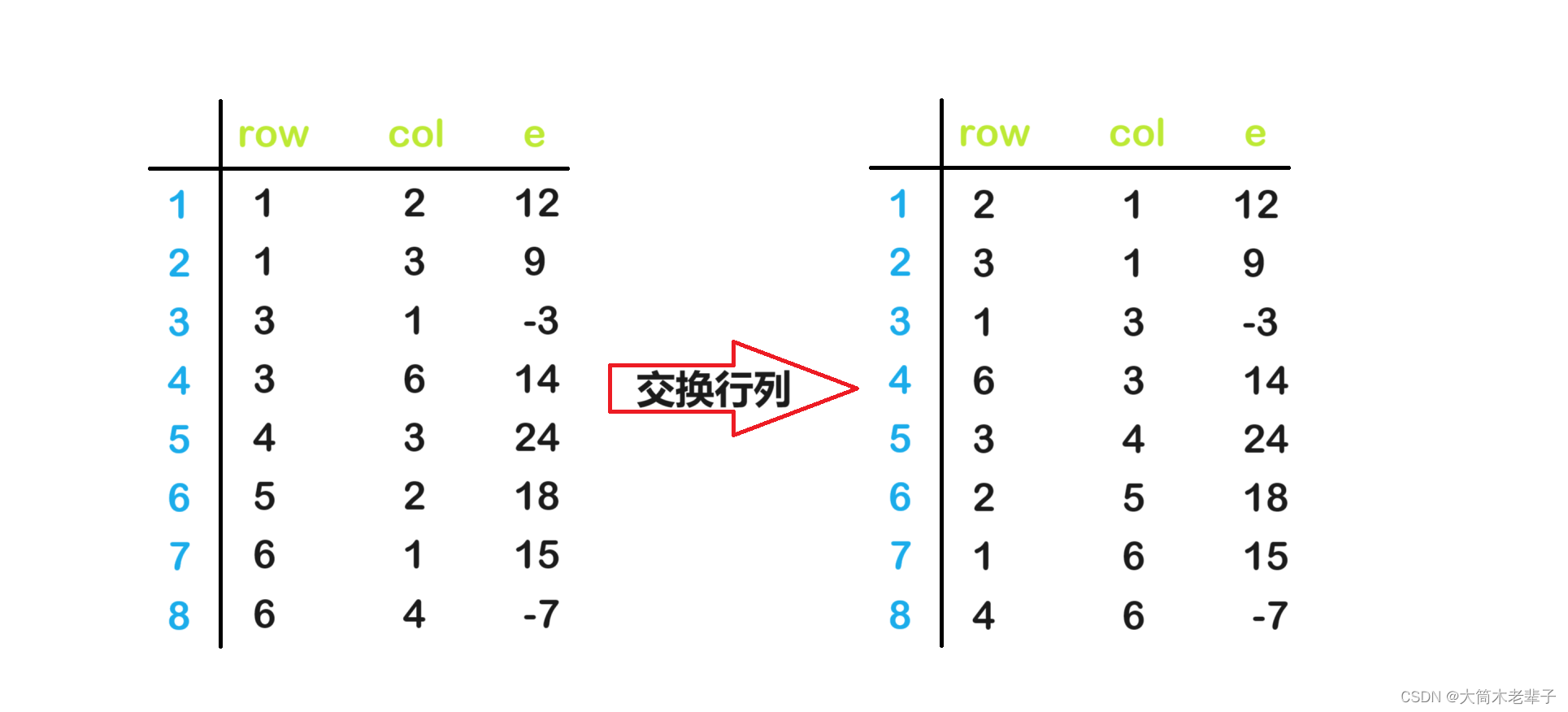
稀疏矩阵的三元组表表示法及其转置
1. 什么是稀疏矩阵 稀疏矩阵是指矩阵中大多数元素为零的矩阵。 从直观上讲,当元素个数低于总元素的30%时,这样的矩阵被称为稀疏矩阵。 由于该种矩阵的特点,我们在存储这种矩阵时,如果直接采用二维数组,就会十分浪费…...

docker安装rabbitMQ,并且创建账号
# 创建docker容器启动,挂到后台运行 docker run -d --name rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq:3.13-management # 打开防火墙 sudo firewall-cmd --zonepublic --add-port5672/tcp --permanent sudo firewall-cmd --zonepublic --add-port15672/tcp --permanent s…...

wireshark解析grpc/protobuf的方法
1,wireshark需要安装3.20以上 下载地址:https://www.wireshark.org/ 2,如果版本不对,需要卸载,卸载方法: sudo rm -rf /Applications/Wireshark.app sudo rm -rf $HOME/.config/wireshark sudo rm -rf /…...
软件测试用例(2)
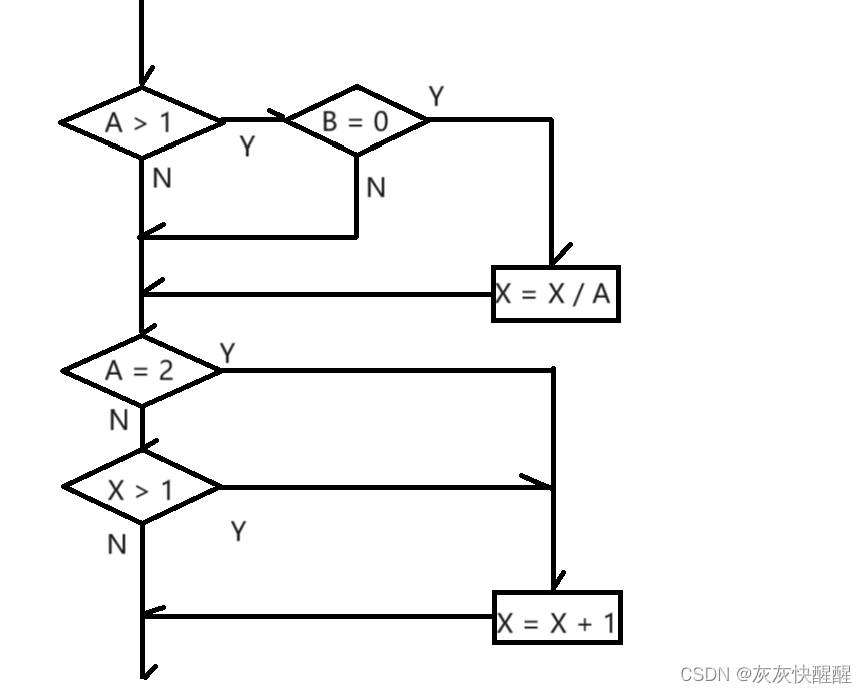
具体的设计方法 -- 黑盒测试 因果图 因果图是一种简化的逻辑图, 能直观地表明程序的输入条件(原因)和输出动作(结果)之间的相互关系. 因果图法是借助图形来设计测试用例的一种系统方法, 特别适用于被测试程序具有多种输入条件, 程序的输出又依赖于输入条件的各种情况. 因果图…...

集群式无人机仿真环境和数据集
仿真环境和数据集 Quick StartAcknowledgementsSwarmSim Quick Start Compiling tests passed on 20.04 with ros installed. You can just execute the following commands one by one. # Download the Simulator and run it wget https://cloud.tsinghua.edu.cn/library/34…...
IPSec VPN
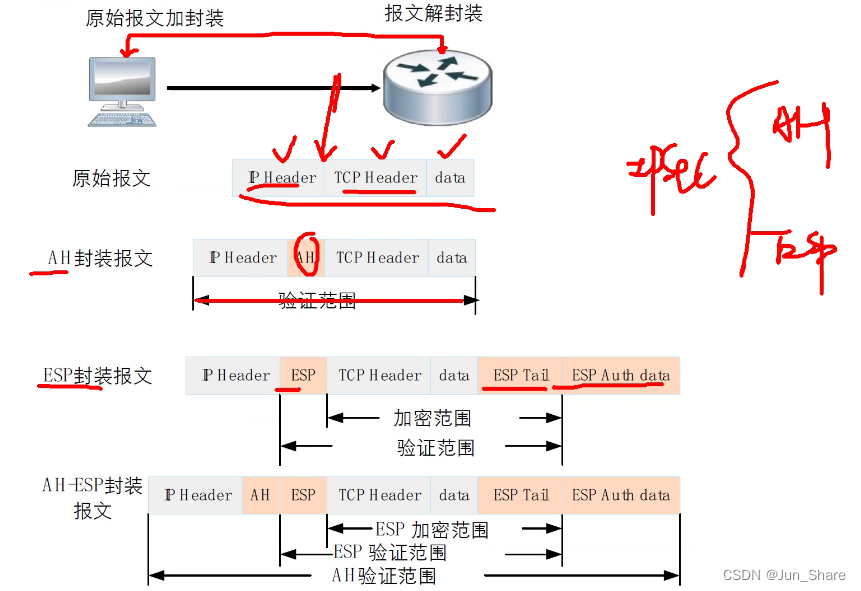
IP Security,IP安全 1、特点 L3的VPN 缺:不支持组播、配置复杂、延迟增加、资源消耗较多 优:具备访问控制、密码学四个维度、抗重放打击 2、组件 ①安全协议 1)验证头技术(AH) IP协议号51 提供数据完整性检查,身份验证,抗重放攻击 无法做数据的机密性 AH的完…...
docker部署nacos,单例模式(standalone),使用内置的derby数据库,简易安装
文章目录 前言安装创建文件夹docker指令安装docker指令安装-瘦身版 制作docker-compose.yaml文件查看页面 前言 nacos作为主流的服务发现中心和配置中心,广泛应用于springcloud框架中,现在就让我们一起简易的部署一个单例模式的nacos,版本可…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
