C++实现二叉搜索树的增删查改(非递归玩法)
文章目录
- 一、二叉搜索树的概念结构和时间复杂度
- 二、二叉搜索树的插入
- 三、二叉搜索树的查找
- 四、二叉搜索树的删除(最麻烦,情况最多,一一分析)
- 3.1首先我们按照一般情况下写,不考虑特殊情况下
- 4.1.1左为空的情况(与右为空的情况差不多)
- 4.1.2两边都不为空的情况下
- 4.1其次我们考虑极端情况,如果刚好是整体树的根要删除
- 五、二叉搜索树的中序遍历
- 六、二叉搜索树的拷贝构造函数,析构函数,赋值操作
- 6.1 赋值操作(比较简单)
- 6.2拷贝构造
- 6.3析构函数
- 七、全部源码展现(递归玩法的代码也传进来了,下次讲解)

先赞后看,养成习惯!!!^ _ ^<3 ❤️ ❤️ ❤️
码字不易,大家的支持就是我坚持下去的动力。点赞后不要忘了关注我哦!
所属专栏:C++进阶
一、二叉搜索树的概念结构和时间复杂度
二叉搜索树(Binary Search Tree)又称二叉排序树(Binary Sort Tree),是一种特殊类型的二叉树,它所有的根节点大于左子树的节点,小于右子树的节点,对二叉搜索树进行中序遍历,即可得到有序的数列。二叉搜索树的时间复杂度由树的高度决定,其搜索、插入和删除的时间复杂度均为 O(log n),其中 n 是节点数。在最坏的情况下,仍然会有 O(n)的时间复杂度。
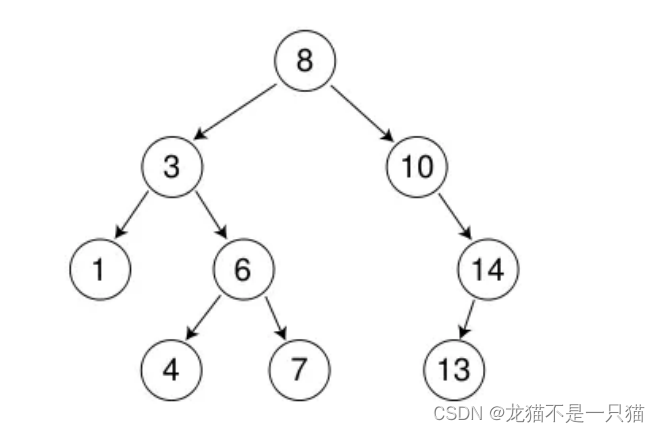
二、二叉搜索树的插入
首先定义一个命名空间作用域,在域中进行插入操作,构造一个二叉树的节点,对节点进行初始化构造
namespace key
{template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;BSTreeNode(const K& key):left(nullptr), right(nullptr),_key(key){}Node* left;Node* right;K _key;};template<class K>class BSTree{public:bool Insert(const K& key){Node* root = new Node(key);if (_root == nullptr){_root = root;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > root->_key){parent = cur;cur = cur->left;}else if (cur->_key < root->_key){parent = cur;cur = cur->right;}else{return false;}}if (parent->_key < root->_key)parent->right = root;elseparent->left = root;return true;}
}
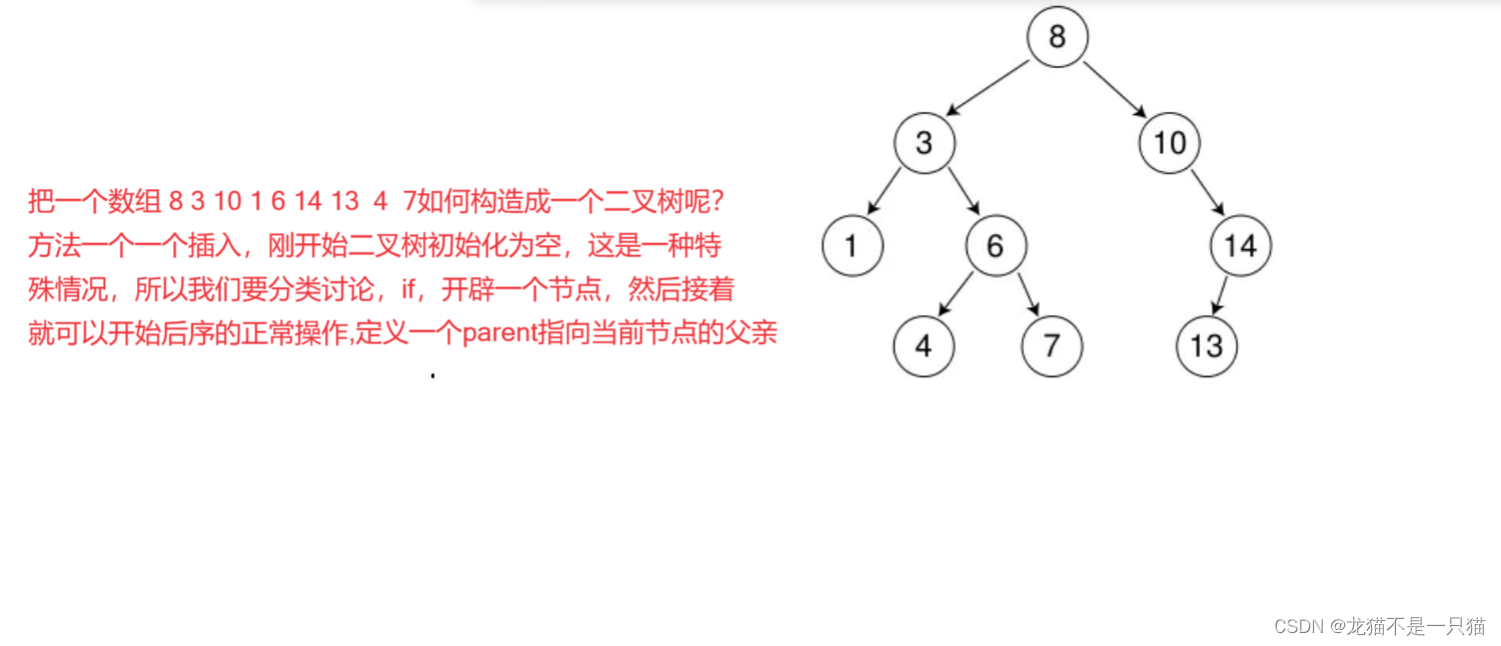
代码图解:
三、二叉搜索树的查找
查找非常简单按照流程找就行了
typedef BSTreeNode<K> Node;
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->right;}else if (cur->_key > key){cur = cur->left;}else{return true;}}return false;
}
四、二叉搜索树的删除(最麻烦,情况最多,一一分析)
3.1首先我们按照一般情况下写,不考虑特殊情况下
bool Erase(const K& key)
{assert(_root);Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->left;}else if (cur->_key < key){parent = cur;cur = cur->right;}else{if (cur->left == nullptr){if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}delete cur;return true;}else if (cur->right == nullptr){if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}delete cur;return true;}else{Node* pminleft = cur;Node* minleft = cur->right;while (minleft->left){pminleft = minleft;minleft = minleft->left;}cur->_key = minleft -> _key;if (minleft == pminleft->left)pminleft->left = minleft->right;elsepminleft->right = minleft->right;delete minleft;return true;}}}return false;
}
代码图解(解释找到时候的情况)
4.1.1左为空的情况(与右为空的情况差不多)

4.1.2两边都不为空的情况下

4.1其次我们考虑极端情况,如果刚好是整体树的根要删除
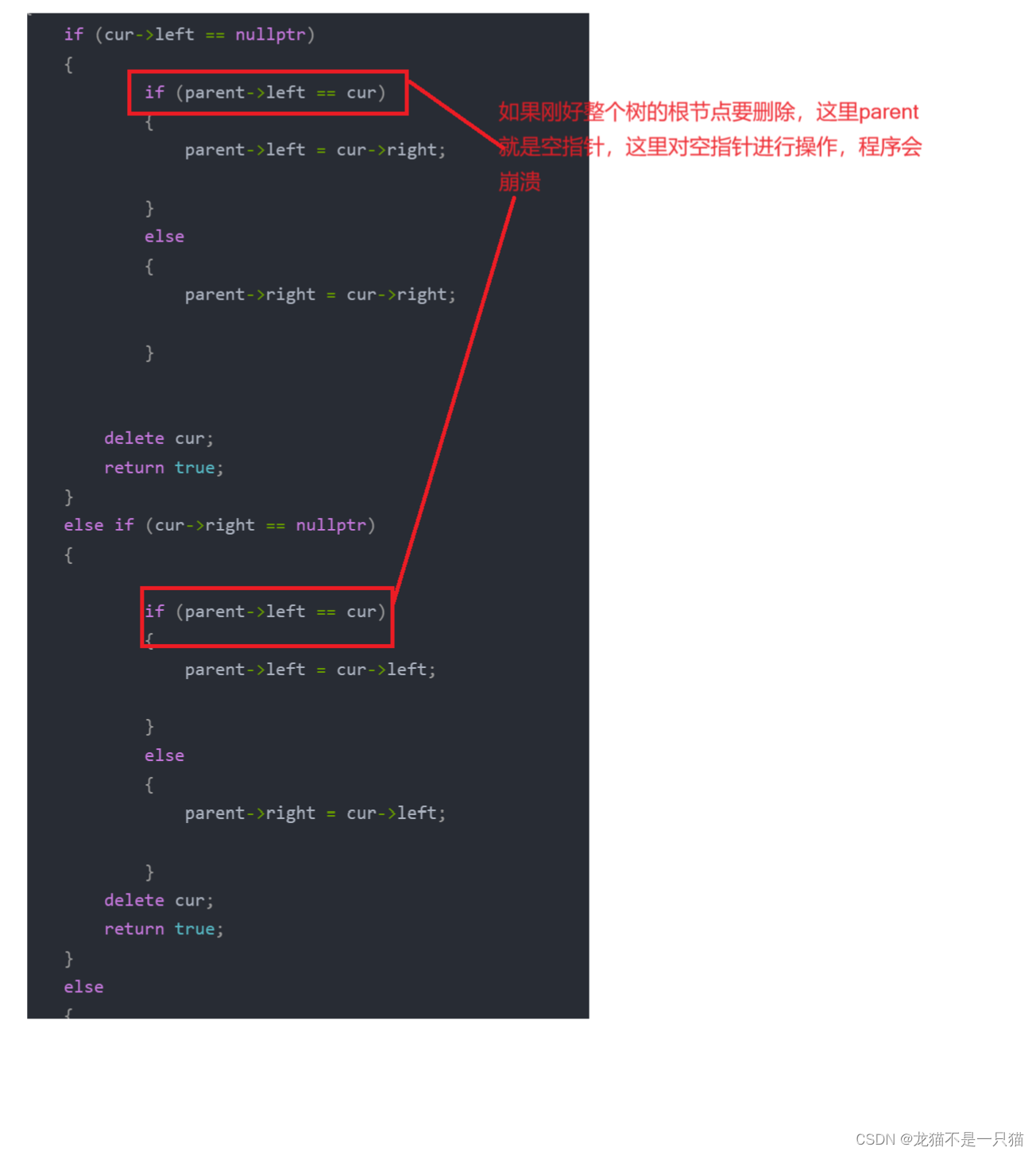
调整代码如下
if (cur->left == nullptr){if (cur == _root){_root = cur->right;}else{if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}}delete cur;return true;}else if (cur->right == nullptr){if (cur == _root){_root = cur->left;}else{if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}}delete cur;return true;
}
五、二叉搜索树的中序遍历
这里我们用了一个小技巧,就是通过类里面的函数调用类里面的私有成员
//中序遍历
void _Inorder()
{Inorder(_root);
}
private://中序遍历void Inorder(Node* root){if (root == nullptr)return;Inorder(root->left);cout << root->_key << ' ';Inorder(root->right);}Node* _root = nullptr;
六、二叉搜索树的拷贝构造函数,析构函数,赋值操作
6.1 赋值操作(比较简单)
BSTree<K>& operator=(const BSTree& root)
{swap(_root, root->_root);return *this;
}
6.2拷贝构造
BSTree(const BSTree<K>& t)
{_root = Copy(t._root);
}
Node* Copy(Node* root)
{if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->left = Copy(root->left);newroot->right = Copy(root->right);return newroot;
}
6.3析构函数
~BSTree()
{Distroy(_root);
}
void Distroy(Node* root)
{if (root == nullptr)return;Distroy(root->left);Distroy(root->right);delete root;
}
七、全部源码展现(递归玩法的代码也传进来了,下次讲解)
#pragma once
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;namespace key
{template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;BSTreeNode(const K& key):left(nullptr), right(nullptr),_key(key){}Node* left;Node* right;K _key;};template<class K>class BSTree{public://查BSTree() = default;//自动生成默认构造~BSTree(){Distroy(_root);}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(const BSTree& root){swap(_root, root->_root);return *this;}typedef BSTreeNode<K> Node;bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->right;}else if (cur->_key > key){cur = cur->left;}else{return true;}}return false;}//增bool Insert(const K& key){Node* root = new Node(key);if (_root == nullptr){_root = root;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > root->_key){parent = cur;cur = cur->left;}else if (cur->_key < root->_key){parent = cur;cur = cur->right;}else{return false;}}if (parent->_key < root->_key)parent->right = root;elseparent->left = root;return true;}//删bool Erase(const K& key){assert(_root);Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->left;}else if (cur->_key < key){parent = cur;cur = cur->right;}else{if (cur->left == nullptr){if (cur == _root){_root = cur->right;}else{if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}}delete cur;return true;}else if (cur->right == nullptr){if (cur == _root){_root = cur->left;}else{if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}}delete cur;return true;}else{Node* pminleft = cur;Node* minleft = cur->right;while (minleft->left){pminleft = minleft;minleft = minleft->left;}cur->_key = minleft -> _key;if (minleft == pminleft->left)pminleft->left = minleft->right;elsepminleft->right = minleft->right;delete minleft;return true;}}}return false;}/ //递归玩法//增bool _InsertR(const K& key){_Insert(_root,key);}bool _EraseR(const K& key){_Erase(_root, key);}bool _FindR(const K& key){_Find(_root,key);}void Distroy(Node* root){if (root == nullptr)return;Distroy(root->left);Distroy(root->right);delete root;}//中序遍历void _Inorder(){Inorder(_root);}private://中序遍历void Inorder(Node* root){if (root == nullptr)return;Inorder(root->left);cout << root->_key << ' ';Inorder(root->right);}bool _Insert(Node*& root,const K& key){if (root == nullptr){Node* newroot = new Node(key);root = newroot;return true;}if (root->_key > key){_Insert(root->left, key);}else if (root->_key < key){_Insert(root->right, key);}elsereturn false;}Node& _Find(Node*& root, const K& key){if (root == nullptr)return nullptr;if (root->_key > key){_Find(root->left);}else if (root->_key < key){_Find(root->right);}else{return root;}}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->left = Copy(root->left);newroot->right = Copy(root->right);return newroot;}bool _Erase(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key > key){return _Erase(root->left,key);}else if(root->_key < key){return _Erase(root->right ,key);}else{Node* minright = root->right;while (minright->left)minright = minright->left;swap(root->_key,minright->_key);minright->right = minright->right;delete minright;return true;}}Node* _root = nullptr;};
}

相关文章:

C++实现二叉搜索树的增删查改(非递归玩法)
文章目录 一、二叉搜索树的概念结构和时间复杂度二、二叉搜索树的插入三、二叉搜索树的查找四、二叉搜索树的删除(最麻烦,情况最多,一一分析)3.1首先我们按照一般情况下写,不考虑特殊情况下4.1.1左为空的情况ÿ…...
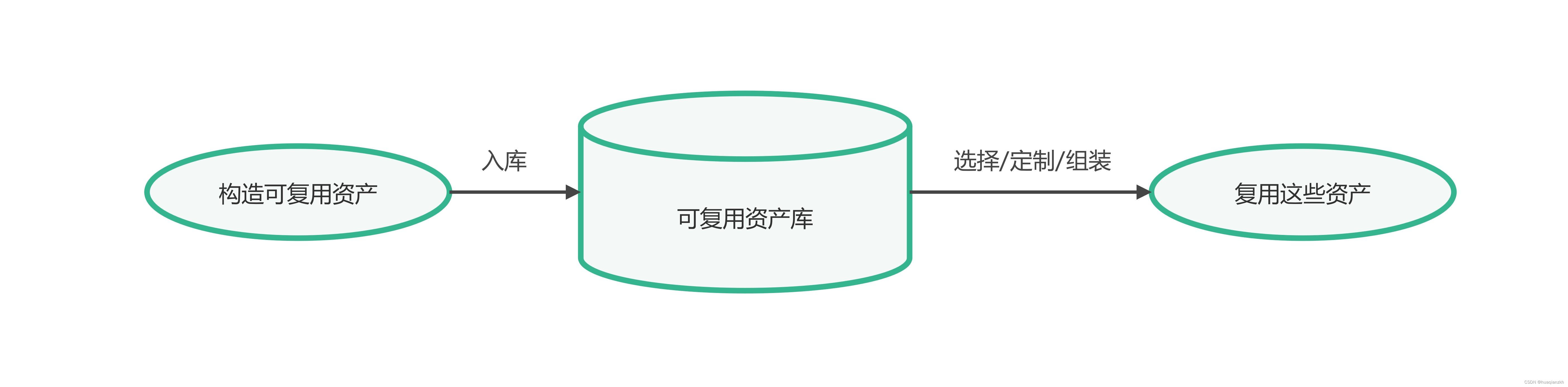
软件架构复用
1.软件架构复用的定义及分类 软件产品线是指一组软件密集型系统,它们共享一个公共的、可管理的特性集,满足某个特定市场或任务的具体需要,是以规定的方式用公共的核心资产集成开发出来的。即围绕核心资产库进行管理、复用、集成新的系统。核心…...
【初阶数据结构】——leetcode:160. 相交链表
文章目录 1. 题目介绍2. 思路1:暴力求解算法思想代码实现 3. 思路2:快慢指针算法思想代码实现 1. 题目介绍 链接: link 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点&…...

【Go】goroutine并发常见的变量覆盖案例
越过山丘 遇见六十岁的我 拄着一根白手杖 在听鸟儿歌唱 我问他幸福与否 他笑着摆了摆手 在他身边围绕着一群 当年流放归来的朋友 他说你不必挽留 爱是一个人的等候 等到房顶开出了花 这里就是天下 总有人幸福白头 总有人哭着分手 无论相遇还是不相遇 都是献给岁月的序曲 …...
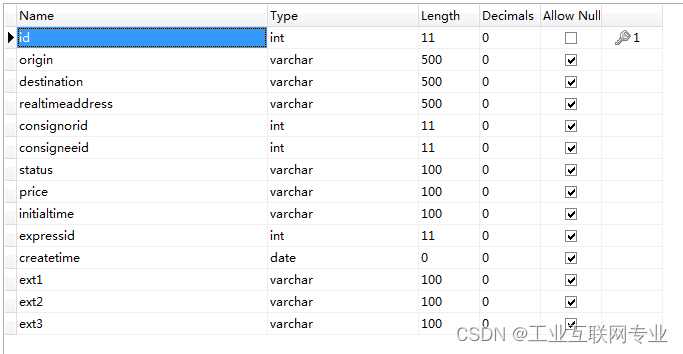
基于SSM+Jsp+Mysql的快递管理系统
开发语言:Java框架:ssm技术:JSPJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包…...

如何动态往Spring容器注册/移除bean?
几个关键点需要知道 本文不谈原理,直接上实战。 几个关键点:如何拿到Spring上下文来创建bean或移除bean?如何准备构建bean所需的BeanDefinition? 第一问:可注入bean工厂org.springframework.beans.factory.support.…...

C语言交换二进制位的奇数偶数位
基本思路 我们要先把想要交换的数的二进制位给写出来假如交换13的二进制位,13的二进制位是 0000 0000 0000 0000 0000 0000 0000 1101然后写出偶数位的二进制数(偶数位是1的) 1010 1010 1010 1010 1010 1010 1010 1010然后写出奇数位的二进…...

爬虫实战三、PyCharm搭建Scrapy开发调试环境
#一、环境准备 Python开发环境以及Scrapy框架安装,参考:爬虫实战一、Scrapy开发环境(Win10Anaconda)搭建 PyCharm安装和破解,参考:爬虫实战二、2019年PyCharm安装(激活到2100年) …...

2012年认证杯SPSSPRO杯数学建模C题(第一阶段)碎片化趋势下的奥运会商业模式全过程文档及程序
2012年认证杯SPSSPRO杯数学建模 C题 碎片化趋势下的奥运会商业模式 原题再现: 从 1984 年的美国洛杉矶奥运会开始,奥运会就不在成为一个“非卖品”,它在向观众诠释更高更快更强的体育精神的同时,也在攫取着巨大的商业价值&#…...

【Next.js】连接 MongoDB 实现基本的接口
【Next.js】连接 MongoDB 实现基本的接口 什么是 MongoDB MongoDB 是由C语言编写的,是一个基于分布式文件存储的开源数据库系统。在高负载的情况下,添加更多的节点,可以保证服务器性能。MongoDB 旨在为WEB应用提供可扩展的高性能数据存储解…...

中值滤波算法与SSE2指令集并行优化
中值滤波算法是经典图像处理中极为常见的操作,一般我们通过调用OpenCV或者是Matlab直接进行使用,以至于有种它本来就很容易实现且速度很快的错觉。近来用到中值滤波算法,因为不想用到OpenCV库或者Matlab而对其实现研究了一番,才发现其中有很多值得注意的细节。下面我们结合…...

2012年认证杯SPSSPRO杯数学建模B题(第二阶段)节能减排全过程文档及程序
2012年认证杯SPSSPRO杯数学建模 节能减排、抑制全球气候变暖 B题 白屋顶计划 原题再现: 第二阶段问题 虽然环境学家对地球环境温度的改变有许多种不同观点,但大多数科学家可以达成一个基本的共识:近年来人类的活动,尤指二氧…...
)
NOI - OpenJudge - 2.5基本算法之搜索 - 2753:走迷宫 - 超级无敌详细题解(含多个不同算法AC代码)
点赞关注吧~ 2753:走迷宫 查看提交统计提问 总时间限制: 1000ms 内存限制: 65536kB 描述 一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;有的格子是空地,可以走。 给定一个迷宫,求从左上角走到右下角最…...

什么是Redis数据一致性?如何解决?
在系统中缓存最常用的策略是:服务端需要同时维护DB和cache,并且是以DB的结果为准–Cache-Aside Pattern(缓存分离模式、旁路缓存) 读数据 单纯的读数据是不会产生数据不一致,只有并发下读和写才会存在数据不一致。 写…...

【办公软件】开发常用网站
文章目录 一、开发社区二、开发学习三、视图工具四、开发工具五、前端web开发工具六、开发接口官网 备用产看。 https://www.webhub123.com https://www.webhub123.com/#/home/detail?projectHashid59183272&ownerUserid22053727 java全栈只是体系:https://www…...

车道线检测_Canny算子边缘检测_1
Canny算子边缘检测(原理) Canny算子边缘检测是一种经典的图像处理算法,由John F. Canny于1986年提出,用于精确、可靠地检测数字图像中的边缘特征。该算法设计时考虑了三个关键目标:低错误率(即尽可能多地检…...

kubadm部署kubernetes
什么是kubernetes Kubernetes是一款应用于集群的,容器自动部署、扩展和管理的开源平台,提供了一种以容器为中心的基础架构。利用kubernetes,你可以快速高效地响应客户如下请求: 应用程序的动态、精准部署应用程序的动态扩展无缝推…...

Sqlite插入单引号和双引号,防止sql注入
1. 方法1 sqlite3_mprintf替换sprintf,%q替换%s. 1.1. 举例 修改前代码 //修改前, hello123写入失败char sql[1000]char* sql sprintf("UPDATE table SET name %s WHERE name_id %d","hello123", 1);rc sqlite3_exec(db, sql, NULL, NULL, &err…...
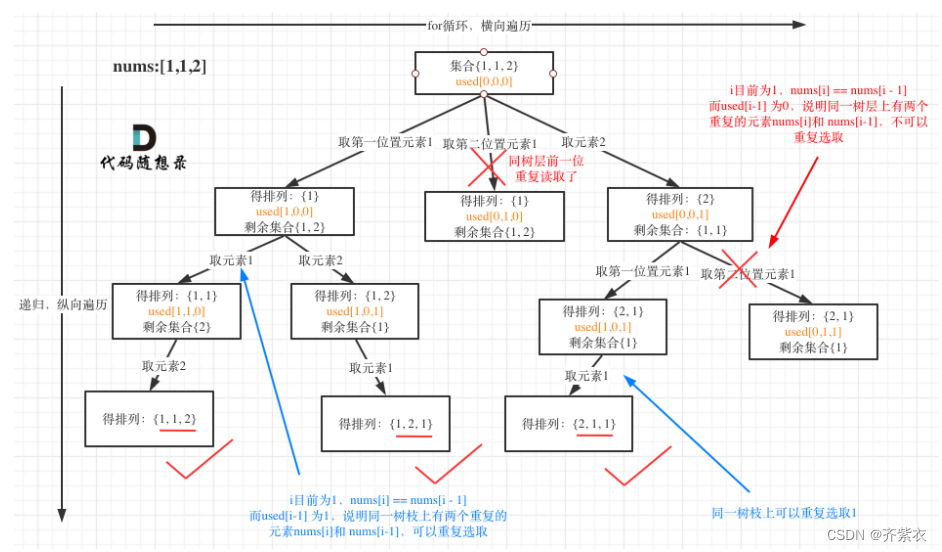
代码随想录算法训练营第二十九天(回溯5)|491. 非递减子序列、46. 全排列、47. 全排列 II(JAVA)
文章目录 491. 非递减子序列解题思路源码 46. 全排列解题思路源码 47. 全排列 II解题思路源码 总结 491. 非递减子序列 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 …...

【CANN训练营笔记】AscendCL图片分类应用(C++实现)
样例介绍 基于PyTorch框架的ResNet50模型,对*.jpg图片分类,输出各图片所属分类的编号、名称。 环境介绍 华为云AI1s CPU:Intel Xeon Gold 6278C CPU 2.60GHz 内存:8G NPU:Ascend 310 环境准备 下载驱动 wget ht…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...