NOI - OpenJudge - 2.5基本算法之搜索 - 2753:走迷宫 - 超级无敌详细题解(含多个不同算法AC代码)
点赞关注吧~
2753:走迷宫
- 查看
- 提交
- 统计
- 提问
总时间限制:
1000ms
内存限制:
65536kB
描述
一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;有的格子是空地,可以走。
给定一个迷宫,求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走,不能斜着走。
输入
第一行是两个整数,R和C,代表迷宫的长和宽。( 1<= R,C <= 40)
接下来是R行,每行C个字符,代表整个迷宫。
空地格子用'.'表示,有障碍物的格子用'#'表示。
迷宫左上角和右下角都是'.'。
输出
输出从左上角走到右下角至少要经过多少步(即至少要经过多少个空地格子)。计算步数要包括起点和终点。
样例输入
5 5 ..### #.... #.#.# #.#.# #.#..
样例输出
9
标准代码及题解
解题
简单的使用bfs或者dfs即可,因为R和C比较小,使用dfs也不会太消耗时间
代码
dfs
①平常做法,找时将地图某值设墙,找完后再设置路
(1)标准
#include <iostream>
using namespace std;
char map[45][45];
int R, C, ans = -1;
int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
void dfs(int x, int y, int step) {if (x == R - 1 && y == C - 1 && (step < ans || ans == -1)) ans = step;int xx, yy;for (int i = 0; i < 4; i++) {xx = x + dir[i][0];yy = y + dir[i][1];if (xx >= 0 && xx < R && yy >= 0 && yy < C && map[xx][yy] == '.') {map[xx][yy] = '#';dfs(xx, yy, step + 1);map[xx][yy] = '.';}}
}
int main() {cin >> R >> C;for (int i = 0; i < R; i++)for (int j = 0; j < C; j++)cin >> map[i][j];dfs(0, 0, 1);cout << ans;
}
(2)本人手写
//DFS 做法
#include <bits/stdc++.h>
using namespace std;
int r,c;//r行 c列
int maze[45][45];
int ans=-1;
int movex[4]{-1,1,0,0};//上下左右
int movey[4]{0,0,-1,1};//上下左右
void dfs(int x,int y,int step){if(x==r&&y==c&&(step<ans||ans==-1)){ans=step;}for(int i=0;i<4;i++){int X,Y;X=x+movex[i];Y=y+movey[i];if(X>0&&X<=r&&Y>0&&Y<=c&&maze[X][Y]==0){maze[X][Y]=1;dfs(X,Y,step+1);maze[X][Y]=0;}}
}
int main(){cin>>r>>c;char node;for(int i=1;i<=r;i++){for(int j=1;j<=c;j++){cin>>node;if(node=='#'){maze[i][j]=1;}else if(node=='.'){maze[i][j]=0;}}}dfs(1,1,1);//dfs(x,y,step)cout<<ans<<endl;return 0;
}
②将路径设值,如果到某处以前到过且经过的长度较小则直接略过,进行减枝,减少递归次数
#include <iostream>
using namespace std;
int R, C, map[45][45], dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; //map记录这点经过的最短步数
void dfs(int x, int y) {int xx, yy;for (int i = 0; i < 4; i++) { //四方xx = x + dir[i][0], yy = y + dir[i][1];if (xx >= 0 && xx < R && yy >= 0 && yy < C && map[x][y] + 1 < map[xx][yy]) {map[xx][yy] = map[x][y] + 1;dfs(xx, yy);}}
}
int main() {cin >> R >> C;char temp;for (int i = 0; i < R; i++)for (int j = 0; j < C; j++) {cin >> temp;map[i][j] = (temp == '.') ? 1e9 : -1;}map[0][0] = 1;dfs(0, 0);cout << map[R - 1][C - 1]; // 步数存在了map里
}
bfs
以前总是不明白为什么bfs适合找最短路径,这次好好思考了一下,可以这样理解,
bfs是从一点出发,将其相邻的各点依次加入到队列之中,然后将其相邻的队列分别求它的相邻队列
如图所示,最外层的点无论选择何种路径,最短路径的长度是已经确定了的且相等
当遇到障碍物时它仍是一层一层的进行下去
如果目标正好在一层上,那么这层所代表的距离就是最短距离,
bfs是一层一层,一圈一圈进行下去的,如果你寻找的点正好在那一圈上最短距离也就求出了,不会存在有其它道路更短的情况,因为每一圈下去都是最短路径
比如如图
有两条路径可以到达,绿色和蓝色,其中绿色较短,蓝色较长,蓝色可能会先到蓝绿交点,但他不会把绿色的路堵住,去走上面的路,而是走绿色接下来的路,因为bfs总是去寻找最短的路,如图红色的路径。
现在表达还是有些混乱,之后再更新修补
①使用队列
#include <iostream>
#include <queue>
using namespace std;
int R, C, step[45][45], dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
char map[45][45];
int main() {cin >> R >> C;for (int i = 0; i < R; i++) cin >> map[i];queue<int> q;q.push(0 * C + 0);step[0][0] = 1;while (!q.empty()) {int x = q.front() / C, y = q.front() % C;q.pop();for (int i = 0; i < 4; i++) {int xx = x + dir[i][0], yy = y + dir[i][1];if (map[xx][yy] == '.' && !step[xx][yy]) {q.push(xx * C + yy);step[xx][yy] = step[x][y] + 1;}}}cout << step[R - 1][C - 1];
}
②数组模拟队列
把队列数组设置的长些,出队列直接前面指向加一,不必真正删除
#include <iostream>
using namespace std;
int R, C, queue[2000], step[45][45], dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
char map[45][45];
int main() {cin >> R >> C;for (int i = 0; i < R; i++) cin >> map[i];step[0][0] = 1;queue[0] = 0 * C + 0;for (int i = 0, have = 0; i <= have; i++) {int x = queue[i] / C, y = queue[i] % C;for (int j = 0; j < 4; j++) {int xx = x + dir[j][0], yy = y + dir[j][1];if (map[xx][yy] == '.' && !step[xx][yy]) {queue[++have] = xx * C + yy;step[xx][yy] = step[x][y] + 1;}}}cout << step[R - 1][C - 1];
}相关文章:
)
NOI - OpenJudge - 2.5基本算法之搜索 - 2753:走迷宫 - 超级无敌详细题解(含多个不同算法AC代码)
点赞关注吧~ 2753:走迷宫 查看提交统计提问 总时间限制: 1000ms 内存限制: 65536kB 描述 一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;有的格子是空地,可以走。 给定一个迷宫,求从左上角走到右下角最…...

什么是Redis数据一致性?如何解决?
在系统中缓存最常用的策略是:服务端需要同时维护DB和cache,并且是以DB的结果为准–Cache-Aside Pattern(缓存分离模式、旁路缓存) 读数据 单纯的读数据是不会产生数据不一致,只有并发下读和写才会存在数据不一致。 写…...

【办公软件】开发常用网站
文章目录 一、开发社区二、开发学习三、视图工具四、开发工具五、前端web开发工具六、开发接口官网 备用产看。 https://www.webhub123.com https://www.webhub123.com/#/home/detail?projectHashid59183272&ownerUserid22053727 java全栈只是体系:https://www…...

车道线检测_Canny算子边缘检测_1
Canny算子边缘检测(原理) Canny算子边缘检测是一种经典的图像处理算法,由John F. Canny于1986年提出,用于精确、可靠地检测数字图像中的边缘特征。该算法设计时考虑了三个关键目标:低错误率(即尽可能多地检…...

kubadm部署kubernetes
什么是kubernetes Kubernetes是一款应用于集群的,容器自动部署、扩展和管理的开源平台,提供了一种以容器为中心的基础架构。利用kubernetes,你可以快速高效地响应客户如下请求: 应用程序的动态、精准部署应用程序的动态扩展无缝推…...

Sqlite插入单引号和双引号,防止sql注入
1. 方法1 sqlite3_mprintf替换sprintf,%q替换%s. 1.1. 举例 修改前代码 //修改前, hello123写入失败char sql[1000]char* sql sprintf("UPDATE table SET name %s WHERE name_id %d","hello123", 1);rc sqlite3_exec(db, sql, NULL, NULL, &err…...
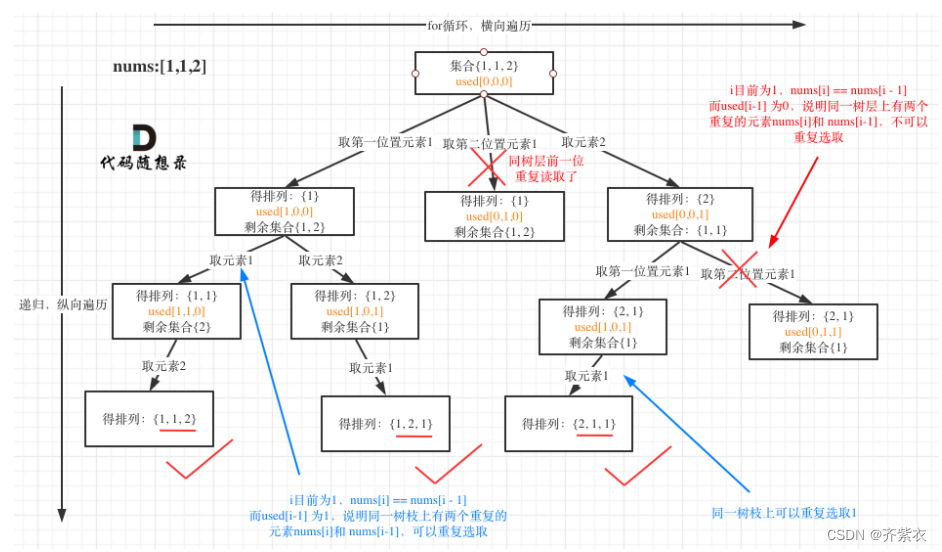
代码随想录算法训练营第二十九天(回溯5)|491. 非递减子序列、46. 全排列、47. 全排列 II(JAVA)
文章目录 491. 非递减子序列解题思路源码 46. 全排列解题思路源码 47. 全排列 II解题思路源码 总结 491. 非递减子序列 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 …...

【CANN训练营笔记】AscendCL图片分类应用(C++实现)
样例介绍 基于PyTorch框架的ResNet50模型,对*.jpg图片分类,输出各图片所属分类的编号、名称。 环境介绍 华为云AI1s CPU:Intel Xeon Gold 6278C CPU 2.60GHz 内存:8G NPU:Ascend 310 环境准备 下载驱动 wget ht…...
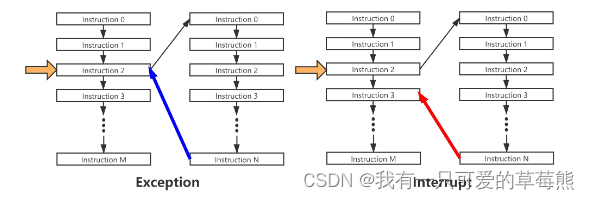
从头开发一个RISC-V的操作系统(二)RISC-V 指令集架构介绍
文章目录 前提ISA的基本介绍ISA是什么CISC vs RISCISA的宽度 RISC-V指令集RISC-V ISA的命名规范模块化的ISA通用寄存器Hart特权级别内存管理与保护异常和中断 目标:通过这一个系列课程的学习,开发出一个简易的在RISC-V指令集架构上运行的操作系统。 前提…...

uniapp/设置桌面角标/发送系统通知/动态修改桌面应用图标/展示3d模型/仿淘宝二楼
uniapp的安卓apk图标角标设置消息数量 1、主要方法: 设置角标: plus.runtime.setBadgeNumber(999) 清除角标: //plus.runtime.setBadgeNumber(0)//没有效果 plus.runtime.setBadgeNumber(-1) //有效果 2、使用在具体的生命周期 1、打开app获取…...

【Java八股学习】Redis高可用 思维导图
说明 文章内容通过学习小林Coding内的优质文章后整理而来,整理成思维导图的方式是为了帮助自己理解、记忆和复习。如若侵权请联系删除,再次对小林Coding内的优质文章表示感谢。参考文章如下: 主从复制是怎么实现的?为什么要有哨…...
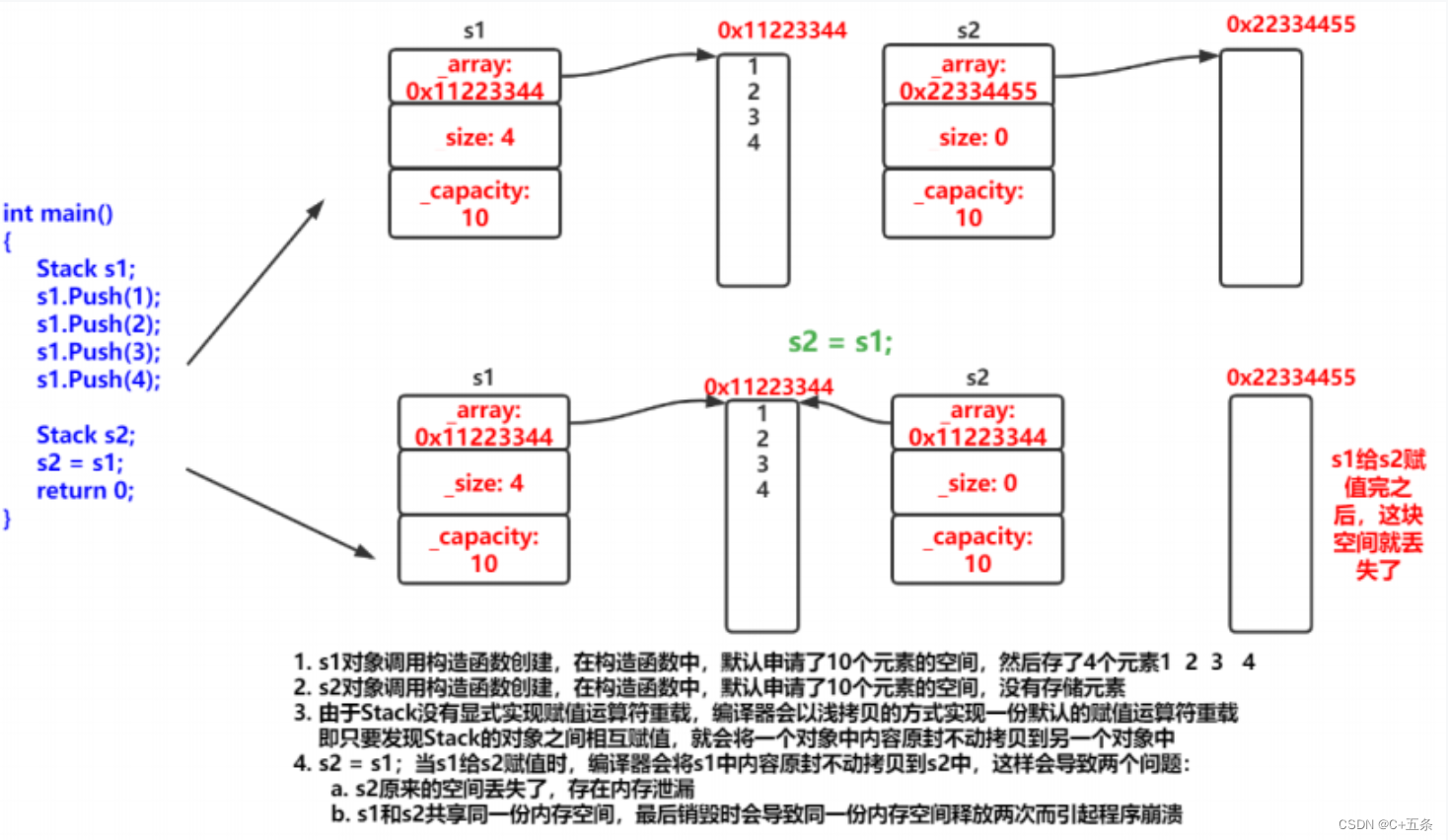
C++万物起源:类与对象(三)拷贝构造、赋值重载
目录 一、拷贝构造函数 1.1拷贝构造函数的概念与特征 1.2拷贝构造的实现 1.3默认构造函数 1.4拷贝构造函数典型调用场景 二、赋值运算符重载 2.1赋值运算符重载的格式 一、拷贝构造函数 1.1拷贝构造函数的概念与特征 在c语言语法中,我们可以将一个变量赋值给…...
)
JavaScript构造函数(new构造js对象与原型链prototype)
构造函数详解 铺垫:面向对象编程一、构造函数是什么?二、构造函数的作用?三、构造函数的执行过程?四、构造函数的返回值?五、构造函数为什么要用new关键字调用?六、构造函数的实例成员和静态成员࿱…...

【WPF应用31】WPF基本控件-ListView的详解与示例
WPF(Windows Presentation Foundation)是.NET框架的一个组成部分,它用于构建桌面应用程序的用户界面。ListView是WPF中一个非常强大的数据展示控件,它可以用来显示一系列的项,类似于Windows资源管理器中的文件列表。Li…...

【动态】江西省小型水库安全监测能力提升试点项目通过验收
近日,由北京国信华源科技有限公司和长江勘测规划设计研究有限责任公司联合承建的江西省小型水库安全监测能力提升试点项目圆满通过验收。 在项目业主单位的组织下,省项目部、特邀专家、县水利局二级项目部以及项目设计、监理、承建等单位的代表组成验收工…...
-声呐驱动)
前视声呐目标识别定位(九)-声呐驱动
前视声呐目标识别定位(一)-基础知识 前视声呐目标识别定位(二)-目标识别定位模块 前视声呐目标识别定位(三)-部署至机器人 前视声呐目标识别定位(四)-代码解析之启动识别模块 …...
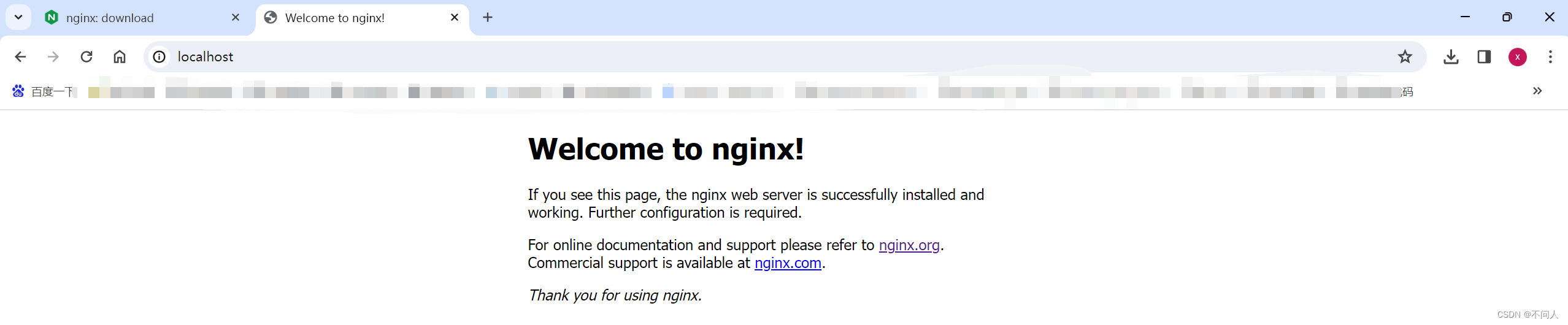
【详解】Windows系统安装Nginx及简单使用
【详解】Windows系统安装Nginx及简单使用 一、Nginx是什么? “Nginx 是一款轻量级的 HTTP 服务器,采用事件驱动的异步非阻塞处理方式框架,这让其具有极好的 IO 性能,时常用于服务端的反向代理和负载均衡。”Nginx 是一款 http 服…...

WebGPU vs. WebGL:前端图形技术的进化与数字孪生的崭新前景
在现代互联网时代,图形渲染在网页应用和数字孪生的开发中起着至关重要的作用。WebGL和WebGPU是两种前端图形技术,它们在处理图形和计算密集型任务时发挥着关键作用。本文将深入研究这两种技术,探讨它们的区别、WebGPU的优势,以及它…...

即刻体验 | 使用 Flutter 3.19 更高效地开发
我们已隆重推出全新的 Flutter 版本——Flutter 3.19。此版本引入了专为 Gemini 设计的新 Dart SDK、一个能让开发者对 Widget 动画实现精细化控制的全新 Widget,Impeller 更新带来的渲染性能提升、有助于实现深层链接的工具和对 Windows Arm64 的支持,以…...
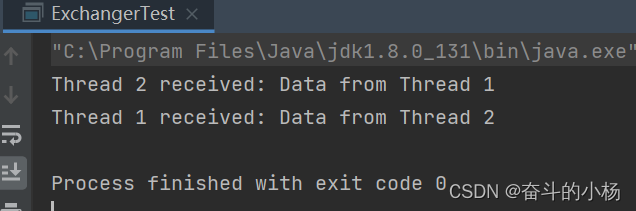
Exchanger 怎么用J.U.C
Exchanger简介 Exchanger通常用来解决以下类似场景的问题,如下:两个线程间需要交换数据的问题,在多线程编程中,经常会有这样的场景:两个线程各自持有一些数据,并且需要在某个点上交换这些数据,…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

华硕电脑,全新的超频方式,无需进入BIOS
想要追求更佳性能释放 或探索更多可玩性的小伙伴, 可能会需要为你的电脑超频。 但我们常用的不论是BIOS里的超频, 还是Armoury Crate奥创智控中心超频, 每次调节都要重启,有点麻烦。 TurboV Core 全新的超频方案来了 4不规…...
数据库管理与高可用-MySQL故障排查与生产环境优化
目录 #1.1MySQL单案例故障排查 1.1.1MySQL常见的故障排查 1.1.2MySQL主从故障排查 #2.1MySQL优化 2.1.1硬件方面的优化 2.1.2进程方面的优化 #3.1MySQL存储引擎 3.1.1 MyISAM存储引擎 3.1.2 InnoDB存储引擎 1.1MySQL单案例故障排查 1.1.1MySQL常见的故障排查 (1&…...

迁移科技3D视觉系统:重塑纸箱拆垛场景的智能革命
一、传统拆垛场景的困局与破局之道 在汽车零部件仓库中,每天有超过2万只异形纸箱需要拆垛分拣。传统人工拆垛面临三大挑战: 效率瓶颈:工人每小时仅能处理200-300件,且存在间歇性疲劳安全隐患:20kg以上重箱搬运导致年…...

Continue 开源 AI 编程助手框架深度分析
Continue 开源 AI 编程助手框架深度分析 一、项目简介 Continue 是一个模块化、可配置、跨平台的开源 AI 编程助手框架,目标是让开发者能在本地或云端环境中,快速集成和使用自定义的 LLM 编程辅助工具。它通过支持 VS Code 与 JetBrains 等主流 IDE 插件…...
