Collection与数据结构 Stack与Queue(一): 栈与Stack
1. 栈
1.1 概念
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据在栈顶。
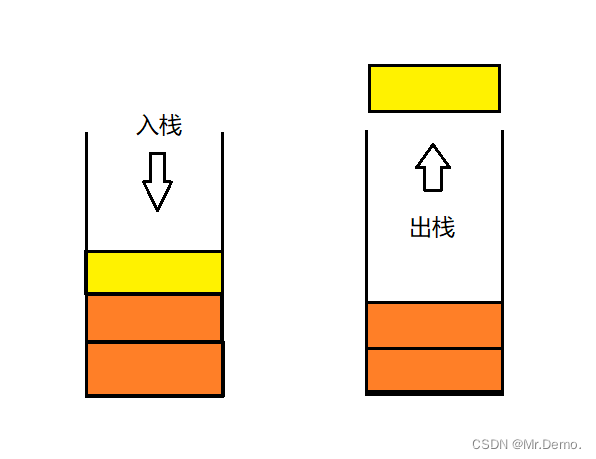
栈在现实生活中的例子:
弹夹:

羽毛球筒:

1.2 栈的使用
| 方法 | 功能 |
|---|---|
| Stack() | 构造一个空的栈 |
| E push(E e) | 将e入栈,并返回e |
| E pop() | 将栈顶元素出栈并返回 |
| E peek() | 获取栈顶元素 |
| int size() | 获取栈中有效元素个数 |
| boolean empty() | 检测栈是否为空 |
import java.util.Stack;public class Main {public static void main(String[] args) {//使用Stack中自带的方法Stack<Integer> stack = new Stack<>();stack.push(1);stack.push(2);stack.push(3);stack.push(4);//压栈System.out.println(stack.peek());System.out.println(stack.peek());//没有弹出元素,只是返回了栈顶元素System.out.println(stack.pop());System.out.println(stack.pop());//出栈System.out.println(stack.size());//计算栈中元素的个数System.out.println(stack.empty());//判断栈是否为空//使用Stack从Collection继承下来的方法Stack<Integer> stack1 = new Stack<>();stack1.add(1);stack1.add(2);stack1.add(3);stack1.add(4);//添加元素System.out.println(stack1.isEmpty());//判断是否为空}
}
运行结果:
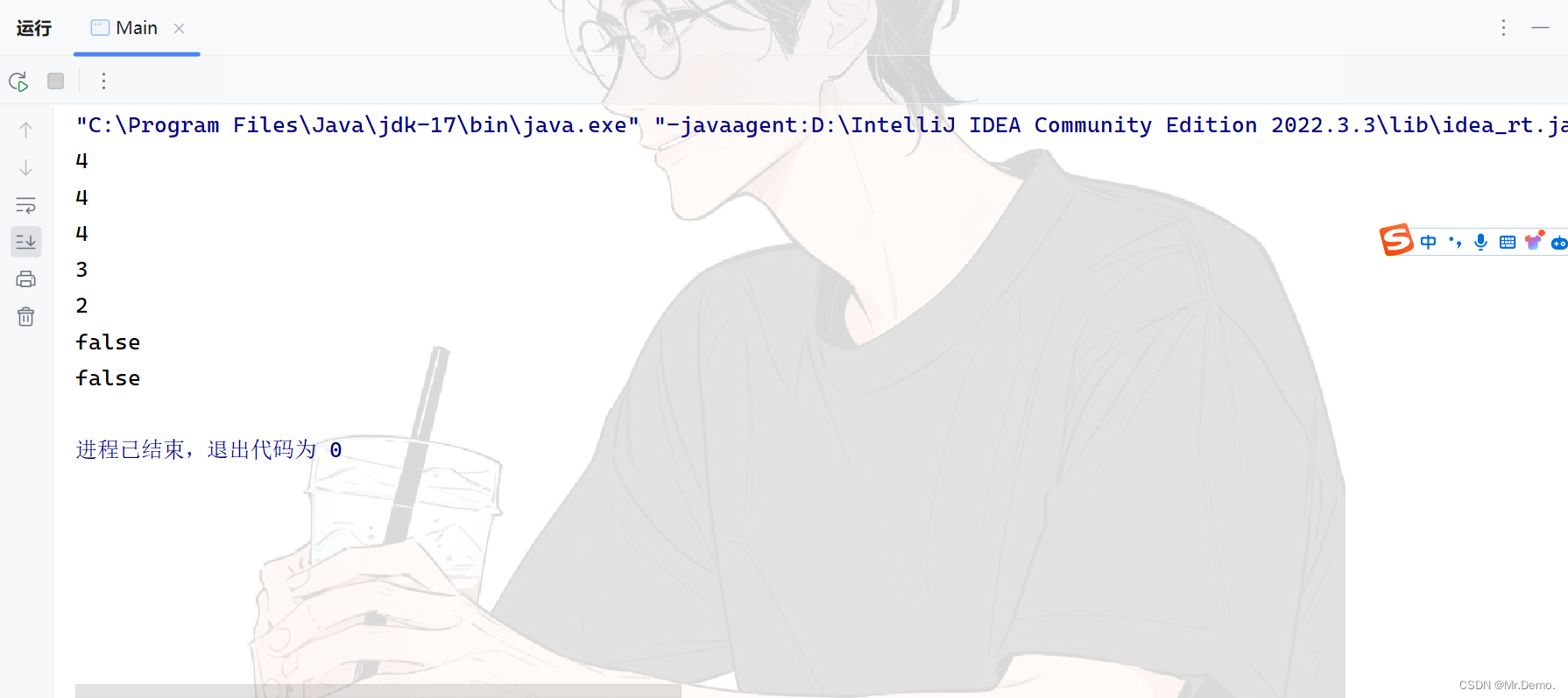
1.3 栈的模拟实现
import java.util.Arrays;public class MyStack {int[] array = new int[5];//默认容积为5int size;public void push(int x){ensureCapacity();array[size] = x;size++;}public int pop(){int e = peek();size--;return e;}public int peek(){if (!empty()){return array[size-1];}throw new EmptyExecption("Stack is empty.");}public boolean empty(){if (size == 0){return true;}return false;}public int size(){return this.size;}private void ensureCapacity(){if (this.array.length == size){this.array = Arrays.copyOf(array,array.length*2);}}
}
public class EmptyExecption extends RuntimeException{public EmptyExecption(String message) {super(message);}
}2. 栈的相关面试题
2.1 括号匹配
OJ链接

class Solution {public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (c == '(' || c == '[' || c == '{') {stack.push(c);//左括号入栈}else {if (stack.empty()){return false;//如果在匹配的时候,栈为空,说明右括号赘余}char ch2 = stack.peek();if (ch2 == '(' && c == ')'||ch2 == '[' && c == ']'||ch2 == '{' && c == '}'){stack.pop();}else {return false;//括号不匹配}}}return stack.empty();//遍历完了,栈中还有元素,说明左括号赘余}}
上述代码逻辑较为复杂,我们通过一张图来理清楚:

2.2 逆波兰表达式求值
OJ链接

class Solution2 {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for (int i = 0; i < tokens.length; i++) {String s = tokens[i];if (isOperation(s)){int x1 = stack.pop();int x2 = stack.pop();//把两个数字出栈int x = 0;if (s.equals("+")){x = x1+x2;} else if (s.equals("-")) {x = x2-x1;//注意逆波兰表达式,先从栈中弹出的放在后面} else if (s.equals("/")) {x = x2/x1;}else {x = x1*x2;}stack.push(x);//计算之后放回栈中}else {stack.push(Integer.parseInt(s));//将字符串转化为数字}}return stack.pop();//最后栈中的值就是最终的值}private boolean isOperation(String s){//判断是否为加减乘除if (s.equals("+") ||s.equals("-")||s.equals("*")||s.equals("/")){return true;}return false;}}拓展: 中缀表达式转后缀表达式,现给出中缀表达式( 1 + 2 ) * ( 3 + 4 ),转为后缀(逆波兰)表达式过程如下.
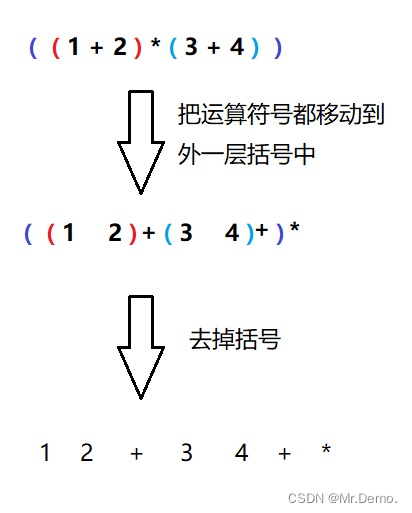
其实我们在电脑中或者是手机上经常用到的计算器就是这样的原理.计算机中的计算器是无法直接识别中缀表达式的,都是先转为后缀表达式,再进行运算的.
2.3 入栈出栈顺序匹配
OJ链接

class Solution3 {public boolean validateStackSequences(int[] pushed, int[] popped) {Stack<Integer> stack = new Stack<>();int j = 0;for (int i = 0; i < pushed.length; i++) {stack.push(pushed[i]);while (!stack.empty() &&stack.peek() == popped[j]){//每放入栈中一个元素,就和popped比较是否相等stack.pop();//如果相等,出栈j++;//popped下标向后走}}while (j < popped.length){//i把push全部遍历完之后,Stack中可能还有元素没有与popped中的匹配完成if (stack.peek() == popped[j]){stack.pop();j++;//继续匹配操作}else {return false;//一旦有一个不匹配,说明popped的出栈顺序是错误的}}return true;//全部匹配完成,返回true}}2.4 在常数时间复杂度的情况下寻找栈中最小元素
OJ链接

class MinStack {Stack<Integer> stack;Stack<Integer> stack1;public MinStack() {stack = new Stack<>();//放所有要入栈的元素stack1 = new Stack<>();//放较小元素,栈顶元素是入stack所有元素中最小的}public void push(int val) {stack.push(val);if (stack1.empty()){//如果最小栈中没有元素,就把第一个元素放入stack1.push(val);}else{if(stack1.peek() >= val){//和最小栈的栈顶元素比较大小,stack1的栈顶大于等于val的时候,入栈//等于的时候也要放入,否则pop的时候,最小栈和普通栈会不匹配stack1.push(val);}}}public void pop() {if (Objects.equals(stack.pop(), stack1.peek())){stack1.pop();//两栈元素相等的时候都弹出,否则只弹出普通栈中的元素}}public int top() {return stack.peek();//返回普通栈栈顶元素}public int getMin() {return stack1.peek();//直接返回最小栈的栈顶元素}}2.5 逆序打印列表
方法一:递归法
void printList(Node head){if(null != head){//遇到null的时候往回递归printList(head.next);//没有遇到null的时候,向后递归System.out.print(head.val + " ");}
}图解:
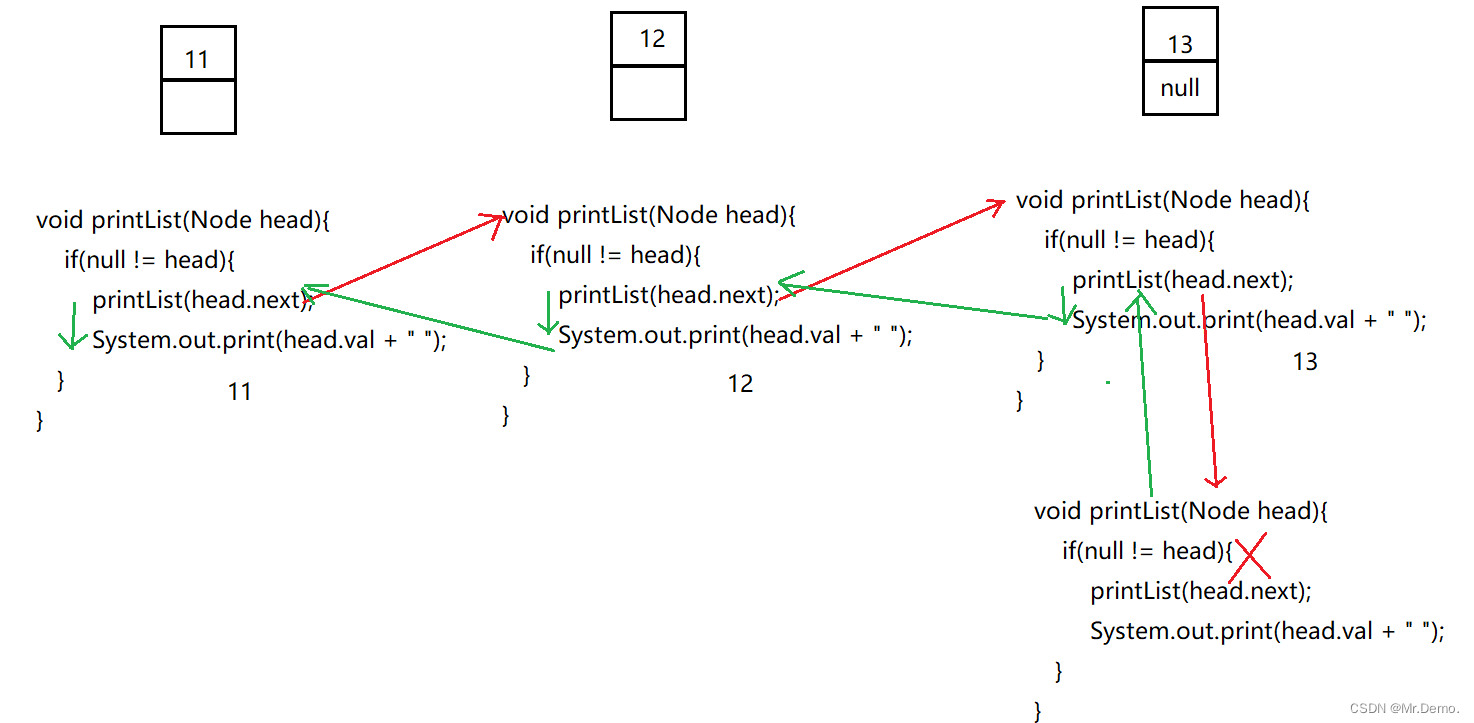
方法二:Stack法
Stack<Node> s = new Stack<>();// 将链表中的结点保存在栈中Node cur = head;while(null != cur){s.push(cur);cur = cur.next;}// 将栈中的元素出栈while(!s.empty()){System.out.print(s.pop().val + " ");}
}
从上述代码,我们可以得到一个结论,栈可以替代递归思想,在我们后期学习二叉树的时候,在非递归遍历二叉树的时候,我们会频繁地用到栈.
相关文章:

Collection与数据结构 Stack与Queue(一): 栈与Stack
1. 栈 1.1 概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压栈&…...

内部类(来自类和对象的补充)
❤️❤️前言~🥳🎉🎉🎉 hellohello~,大家好💕💕,这里是E绵绵呀✋✋ ,如果觉得这篇文章还不错的话还请点赞❤️❤️收藏💞 💞 关注💥&a…...

Android 高德地图
1.获取Key 进入高德开放平台控制台,创建一个新应用。在创建的应用上点击"添加key"按钮,在弹出的对话框中,依次输入key名称,选择服务平台为“Android平台”,输入发布版安全码 SHA1、以及 Package。 获取 S…...

代码随想录|Day31|贪心06|738.单调递增的数字
738.单调递增的数字 思路: 1. 从右向左遍历 从字符串的最后一位向前遍历,即从低位到高位进行检查。这是因为当我们修改某一位数字时,可能会影响到更低位的数字。 2. 检查并修改数字 在遍历过程中,如果发现当前位数字小于其前一位&…...

机械制造学习笔记
一、切削加工、切削运动的基本概念及刀具切削过程 切削加工: 定义:切削加工是利用切削刀具对工件进行切削,以去除多余材料并得到所需形状和尺寸的加工方法之一。应用:广泛应用于金属加工、木材加工、塑料加工等领域,是…...

Golang | Leetcode Golang题解之第3题无重复字符的最长子串
题目: 题解: func lengthOfLongestSubstring(s string) int {// 哈希集合,记录每个字符是否出现过m : map[byte]int{}n : len(s)// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动r…...
SWM341系列应用(上位机应用)
SWM341系列之上位机应用 1、分级图像和PNG、JPG的应用 现象:客户使用SWM34SVET6HMI_0.4.1版本上位机进行UI界面布局,反馈在模拟运行时(PC端)流畅,在Demo平台(设备端)运行卡顿。 分析及解决&…...
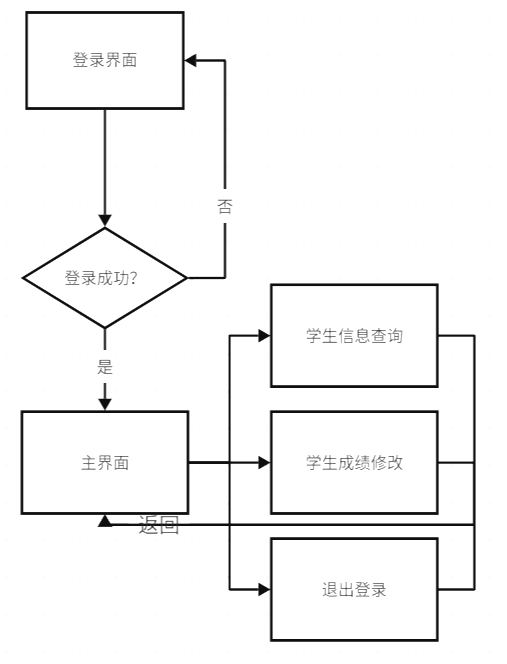
【软件工程】详细设计(一)
1. 引言 1.1 编写目的 该文档的目的是描述《学生成绩管理系统》项目的详细设计,其主要内容包括: 系统功能简介 系统详细设计简述 各个模块的实现逻辑 最小模块组件的伪代码 本文档的预期的读者是: 开发人员 项目管理人员 测试人员 …...
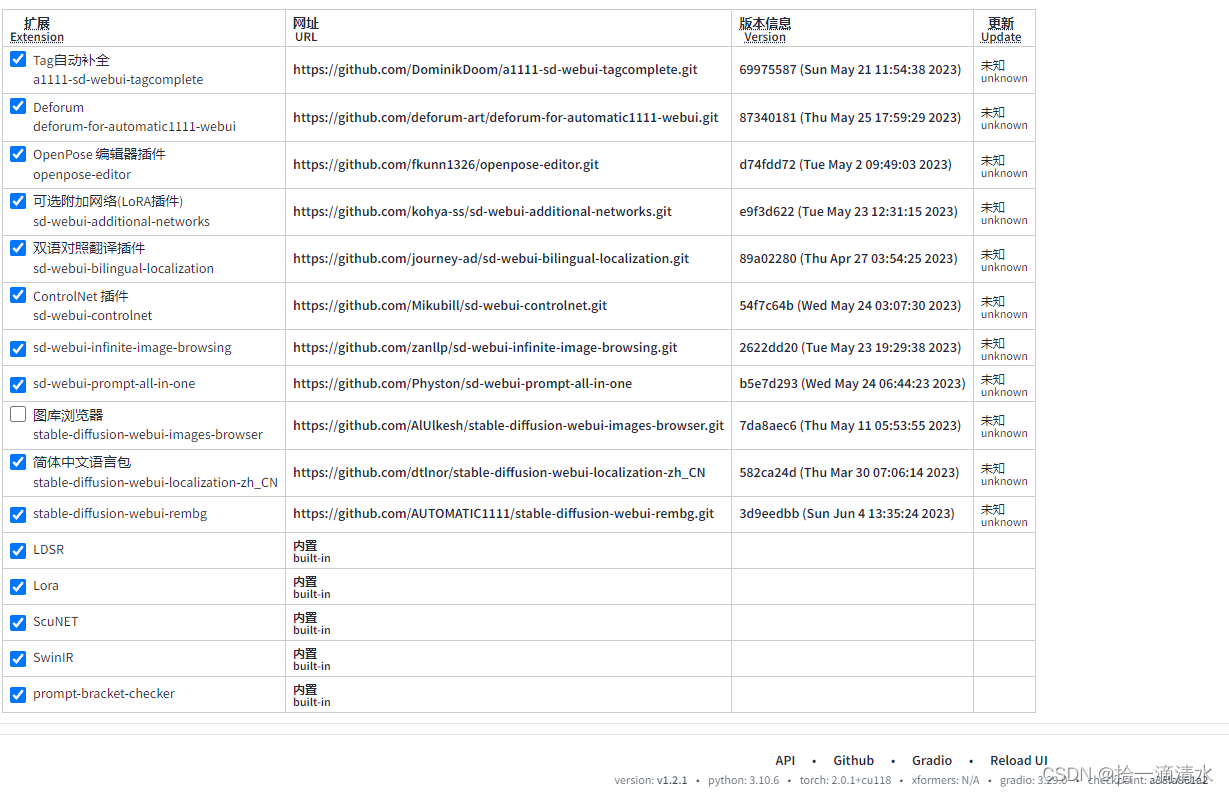
【AIGC】如何在Windows/Linux上部署stable diffusion
文章目录 整体安装步骤windows10安装stable diffusion环境要求安装步骤注意事项参考博客其他事项安装显卡驱动安装cuda卸载cuda安装对应版本pytorch安装git上的python包Q&A linux安装stable diffusion安装anaconda安装cudagit 加速配置虚拟环境挂载oss(optional…...
基于java实现的弹幕视频网站
开发语言:Java 框架:ssm 技术:JSP JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclip…...

【大数据存储】实验4 NoSQL数据库
实验4 NoSQL数据库 NoSQL数据库的安装和使用实验环境: Ubuntu 22.04.3 Jdk 1.8.0_341 Hadoop 3.2.3 Hbase 2.4.17 Redis 6.0.6 mongdb 6.0.12 mogosh 2.1.0 Redis 安装redis完成 新建终端启动redisredis-server新建一个终端redis-cli 建表操作 尝…...

从零学算法80
80. 删除有序数组中的重复项 II 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外…...
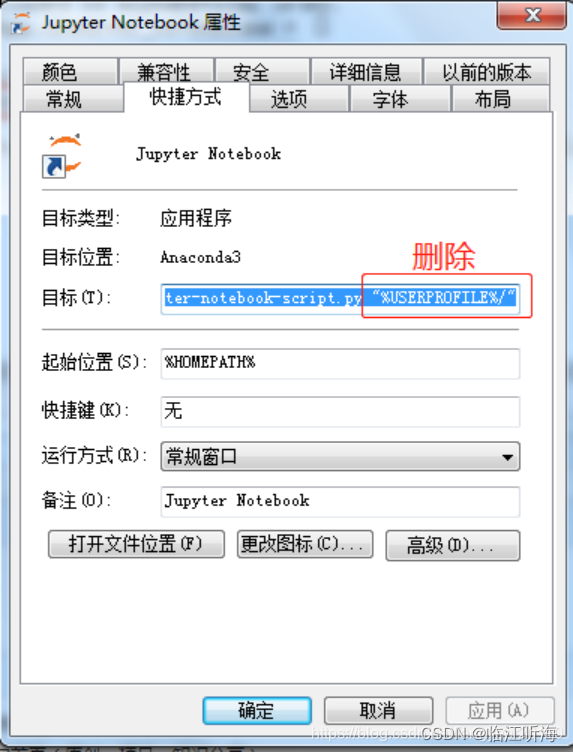
Jupyter notebook文件默认存储路径以及更改方法
初次使用Jupyter Notebook,确实好用啊!但安装Anaconda后,打开Jupyter Notebook 的时候,新建文件的默认存储路径一般在C系统盘下面的XXX目录,那么路径是什么呢?我想把文件保存到其他的文件夹下应该怎么做呢&…...
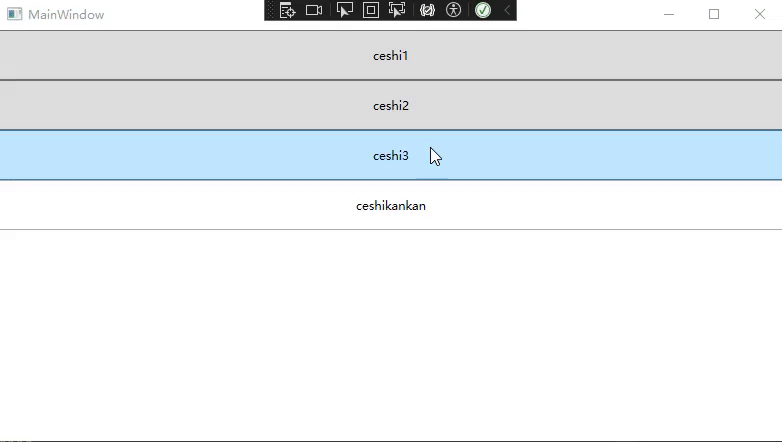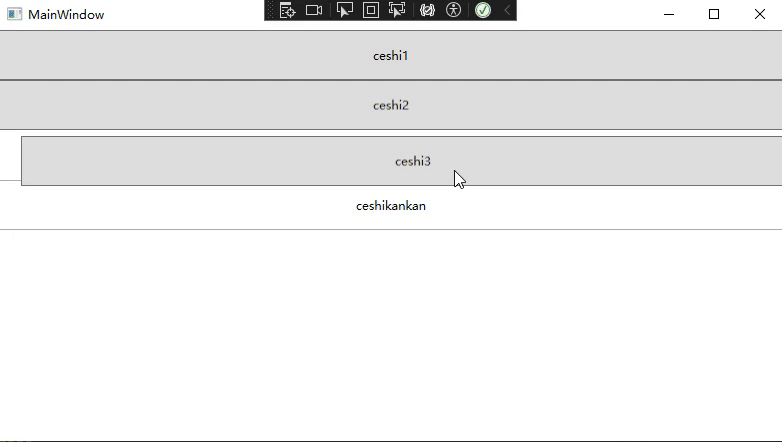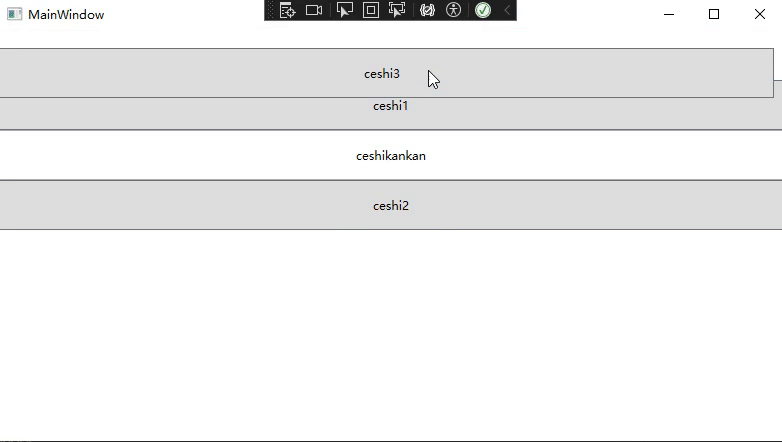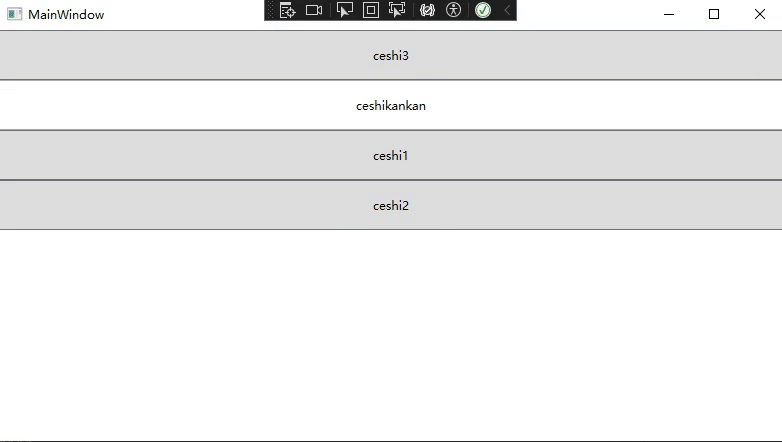
WPF中通过自定义Panel实现控件拖动
背景 看到趋时软件的公众号文章(WPF自定义Panel:让拖拽变得更简单),发现可以不通过Drag的方法来实现ListBox控件的拖动,而是通过对控件的坐标相加减去实现控件的位移等判断,因此根据文章里面的代码,边理解边…...

Centos7安装Docker与Docker-compose【图文教程】
个人记录 查看一下系统是否已经安装了Docker yum list installed | grep docker如下图代表没有安装Docker 卸载已有Docker yum remove docker docker-common docker-selinux docker-engine切换目录 cd /etc/yum.repos.d/查看当前目录所有的镜像源 ll安装yum-util与devi…...

mac电脑maven配置环境变量
1、下载maven https://maven.apache.org 2、配置环境变量 vim .bash_profile JAVA_HOME/Library/Java/JavaVirtualMachines/jdk-1.8.jdk/Contents/Home PATH$JAVA_HOME/bin:$PATH export JAVA_HOME export PATH#maven export MAVEN_HOME/Users/haines/desktop/work/java/a…...
后端返还二进制excl表格数据时候,如何实现在前端下载表格功能及出现表格打开失败的异常处理。
背景: 后端返还一个二进制流的excl表格数据,前端需要对其解析,然后可提供给客户进行下载。 思路:把二进制流数据转换给blob对象,然后利用a标签进行前端下载。 代码: 后端返还 类似如下的数据 前端代码…...
搞学术研究好用免费的学术版ChatGPT网站-学术AI
学术版ChatGPThttps://chat.uaskgpt.com/mobile/?user_sn88&channelcsdn&scenelogin 推荐一个非常适合中国本科硕士博士等学生老师使用的学术版ChatGPT, 对接了超大型学术模型,利用AI技术实现学术润色、中英文翻译,学术纠错&#…...

vue3从精通到入门9:计算属性computed
在 Vue 3 中,computed 是一个用于创建计算属性的工具,它基于组件的响应式依赖进行复杂的计算,并返回一个新的响应式引用。计算属性是 Vue 的一个核心概念,它提供了一种声明式的方式来执行基于其依赖的响应式数据的计算。 compute…...

kafka面试常见问题
1、如何判断kafka某个主题消息堆积? 要判断Kafka中某个主题的消息是否堆积,可以通过查看该主题的生产者和消费者的偏移量(offset)差异来实现。Kafka中的每条消息在主题的分区内都有一个唯一的偏移量,生产者每发送一条…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
