2024053期传足14场胜负前瞻
2024053期售止时间为4月6日(周六)21点00分,敬请留意:

本期深盘多,1.5以下赔率1场,1.5-2.0赔率8场,其他场次是平半盘、平盘。本期14场难度中等。以下为基础盘前瞻,大家可根据自身判断,复选增加防单。

1、埃弗顿 VS 伯恩利
经过连续四轮联赛的稳健表现,伯恩利队成功积累了宝贵积分,显示出保级决心和实力。尽管埃弗顿队近期成功脱离了降级区,但他们已经连续13轮联赛未能品尝胜果。考虑到双方的近期表现与状态,本轮联赛的交锋预计将以握手言和的方式告终。
2、富勒姆 VS 纽卡斯尔联
在过去的五场与富勒姆的比赛中,双方均未能取得胜利,其中四场比赛未能取得进球,这充分展示了双方实力之间的明显差距。此外,富勒姆在近两场面对保级球队的比赛中,每场失去了三个球,其后防线存在严重的问题。因此,可以预见,富勒姆在这场比赛中将面临巨大的挑战和困难。
3、狼队 VS 西汉姆联
两队在近10次交锋中各取得5场胜利,展现出势均力敌的态势。考虑到双方近期均遭遇多场不胜的困境,本场比赛双方握手言和的可能极大。

4、阿斯顿维拉 VS 布伦特福德
阿斯顿维拉在主场比赛中的表现十分出色,已经连续两场获得胜利。在这两场比赛中,他们平均每场攻入3个球,且没有失球,显示出强大的攻击力和防守能力。现在阿斯顿维拉将在联赛中迎战下游球队布伦特福德。坐拥主场之利,阿斯顿维拉有望再次取得胜利。
5、卢顿 VS 伯恩茅斯
卢顿队近期表现欠佳,连续四场联赛主场未能取得胜利,形势不容乐观。相比之下,伯恩茅斯队近期状态出色,过去五轮联赛取得了四胜一平的不败战绩。因此卢顿队在本场比赛中主场沦陷的可能较大。
6、布赖顿 VS 阿森纳
阿森纳本赛季客场作战表现优异,胜率高达60%。更为值得一提的是,球队在联赛客场比赛中平均每场能够攻入2.27个进球,展现出其强大的客场进攻能力。相比之下布赖顿近期因伤病增多导致球队实力下滑,竞争力明显减弱。综合考虑,阿森纳本场比赛有望取得胜利,顺利带走3分。

7、柏林联合 VS 勒沃库森
勒沃库森在本赛季联赛表现出色,以23胜4平的不败战绩傲视群雄,积分榜上遥遥领先。考虑到他们客场胜率高达84.62%,这一数据在本赛季德甲联赛中名列前茅,我们有理由相信他们在本场比赛中将再次展现强大的实力。尽管柏林联合在过去的交锋中占据优势,但勒沃库森依然有能力在这场比赛中取得胜利,凯旋而归。
8、弗赖堡 VS 莱比锡红牛
RB莱比锡在过去的四轮联赛中表现出色,以三胜一平的成绩保持不败,同时球队在进攻和防守两端有出色的发挥,总得分达到了11比2。此外,在过去的十次与费雷堡的交锋中,RB莱比锡也取得了六胜四平的优异战绩。综合以上因素,我们有理由相信RB莱比锡在此役中有望全取三分,继续保持其不败的战绩。
9、海登海姆VS 拜仁慕尼黑
海登海姆近期在联赛中表现欠佳,已经连续6轮未能取得胜利,其中有3场比赛更是遭遇了失利,球队整体状态陷入低迷。相对而言,拜仁慕尼黑在近的一场比赛中失利,士气受挫,急需一场胜利来提振球队士气。考虑到拜仁在双方近两次交锋中展现出了强大的进攻实力,我们有理由期待拜仁能够在这场比赛中以一场大胜来重振旗鼓,找回胜利的节奏。

10、多特蒙德 VS 斯图加特
多特蒙德在上轮客场比赛中成功击败了长期以来的劲敌拜仁,终结了多年的不胜纪录,这无疑极大地提升了球队的士气。值得进一步关注的是,多特蒙德近期在各项赛事中连续多场至少攻入2球,展现出稳定的得分能力。在本轮比赛中,他们将迎战争四的对手斯图加特。考虑到斯图加特在上轮比赛中意外地未能取得胜利,多特蒙德有望借助主场之利和士气高涨的优势,取得本场比赛的胜利。
11、罗马 VS 拉齐奥
在罗马更换主教练后,其在意甲联赛的表现引起了广泛关注。全队的精神面貌焕然一新,展现出了新的活力和斗志。即使面对实力强劲的拉齐奥,该队在意甲取得两连胜的背景下,罗马在主场也有足够的实力与之一战,保住一场平局。
12、恩波利 VS 都灵
尽管都灵的进攻表现不尽如人意,但他们凭借着坚如磐石的防守策略,在赛场上屡次抢得分数。本赛季,他们平均每场比赛仅失0.87球,这一数据在联赛中堪称上乘。面对近期表现糟糕且进攻能力有限的恩波里队,都灵有望凭借稳固的防守实现比赛胜利。

13、毕尔巴鄂竞技 VS 马洛卡
毕尔巴鄂竞技在与马洛卡的近十次交锋中表现出色,取得了五胜四平的战绩,仅有一场失利。值得一提的是,二月初的一场比赛中,他们曾以四球大胜对手。这些成绩充分展示了毕尔巴鄂竞技球员们的实力和信心。因此毕尔巴鄂竞技在本场比赛中决心要再次取得胜利,为荣誉而战。
14、里斯本竞技 VS 本菲卡
经过对两队在联赛中的整体表现进行深入分析,我们发现它们的发挥接近,均展现出显著的优势,远超过其他球队。我们有理由预测,在本场比赛中,双方可能会展开一场激烈而紧张的对决,终可能会以平局收场。
编辑:大彩虹足球(dacaihong168)
相关文章:

2024053期传足14场胜负前瞻
2024053期售止时间为4月6日(周六)21点00分,敬请留意: 本期深盘多,1.5以下赔率1场,1.5-2.0赔率8场,其他场次是平半盘、平盘。本期14场难度中等。以下为基础盘前瞻,大家可根据自身判断…...

C语言------冒泡法排序
一.前情提要 1.介绍 冒泡法排序法: 1)冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地遍历要排序的列表,一次比较相邻的两个元素,并且如果它们的顺序错误就将它们交换过来。重复这个过程直到没有需…...
学习笔记_Enum枚举类型【十三】)
C#(C Sharp)学习笔记_Enum枚举类型【十三】
什么是枚举类型 枚举类型(Enum) 是由基础整型数值类型的一组命名常量定义的值类型。枚举包含自己的值,但不能继承或传递继承。 语法 // enum enum_name // enum_name variable enum_name.enum_value// 定义一个枚举类型——例如: enum enum_name {va…...
乐知付-如何制作html文件可双击跳转到指定页面?
标题: 乐知付-如何制作html文件可双击跳转到指定页面? 标签: [乐知付, 乐知付加密, 密码管理] 分类: [网站,html] 为了便于买家理解使用链接进行付费获取密码;现开发个小工具,将支付链接转为浏览器可识别的文件,双击打开即可跳转到…...

电工技术学习笔记——直流电路及其分析方法
一、直流电路 电路的组成 1. 电压和电流的参考方向 电压(Voltage):电压是电场力对电荷产生的作用,表示为电荷单位正电荷所具有的能量。在电路中,电压通常被定义为两点之间的电势差,具有方向性,…...

详解python中的迭代
如果给定一个list或tuple,我们可以通过for循环来遍历这个list或tuple,这种遍历我们称为迭代(Iteration)。 在Python中,迭代是通过for ... in来完成的,而很多语言比如C语言,迭代list是通过下标完…...
)
机器学习模型——集成算法(三)
前面我们说了bagging算法和Boosting算法 接下来我们学习Adaboost算法 Adaboost基本概念: AdaBoost (Adaptive Boosting,自适应提升): 算法原理是将多个弱学习器进行合理的结合,使其成为一个强学习器。 Adaboost采用…...
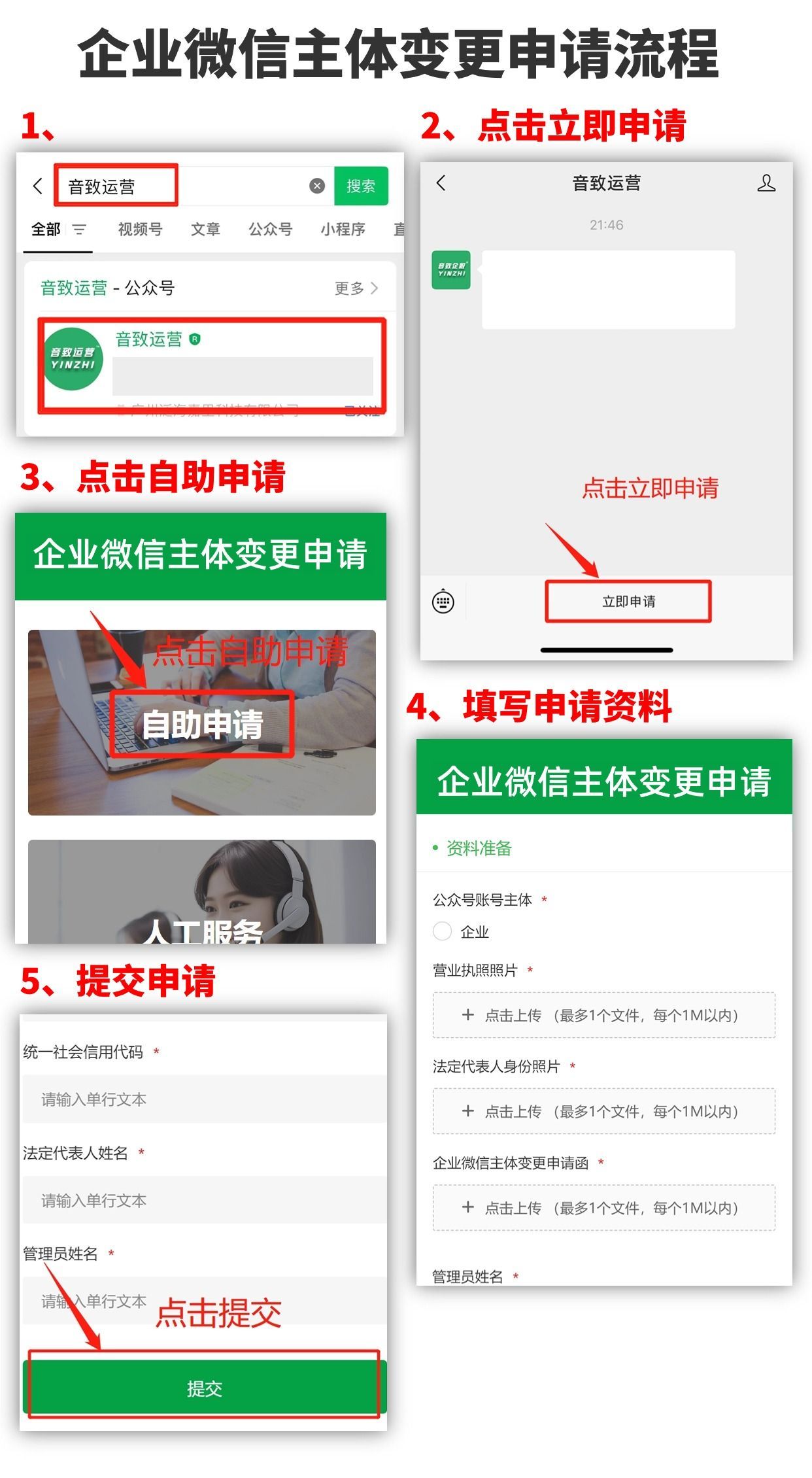
企业微信企业主体变更认证介绍
企业微信变更主体有什么作用? 说一个自己亲身经历的事情,当时我在一家教育公司做运营,公司所有客户都是通过企业微信对接的。后来行业整顿,公司不得不注销,换了营业执照打算做技能培训,但发现注销后原来的企…...

如何降低AI功耗? —— 超低功耗的仿生硬件
一、背景 仿生硬件(Bionic Hardware)这一术语通常指的是受自然界的生物系统启发而设计制造的电子或机械硬件设备,它们在功能、结构、材料、能源效率等方面模仿生物体的特性,以实现更高效、智能、自适应或环境友好的性能。在人工智…...

原型模式详解
原型模式简单的理解来说,就是复制品,用一个已经做好的成品作为原型,然后通过复制它得到新的产品。就好像细胞分裂一样。用Java来说,就是用对象创建对象,而不是通过类来创建对象。 原型模式的目的是从原型实例克隆出新的实例 ,对于那些有非常复杂的初始化过程的对象或者是…...

嵌入式开发中状态模式实现
文章目录 状态模式代码实现代码解释小结 状态模式 状态模式(State Pattern)是一种行为设计模式,它允许对象在内部状态改变时改变它的行为。在嵌入式系统中,状态模式尤其适用于那些根据外部事件或内部条件频繁改变状态并且每种状态…...

目标检测——车牌数据集
一、重要性及意义 交通安全与管理:车牌检测和识别技术有助于交通管理部门快速、准确地获取车辆信息,从而更有效地进行交通监控和执法。例如,在违规停车、超速行驶等交通违法行为中,该技术可以帮助交警迅速锁定违规车辆࿰…...

FOC算法中为啥用PWM触发ADC中断
在FOC(Field Oriented Control,场向量控制)算法中,为什么要使用PWM(Pulse Width Modulation,脉宽调制)触发ADC(Analog-to-Digital Converter,模数转换器)中断…...

2024.4.5学习记录————嵌入式学习内容
2024.4.5学习记录————嵌入式学习内容 C语言 指针,位操作,结构体字节对齐,位段,宏的高级运用 C 基础特性:类,对象,派生,继承,运算符重载,友元…...
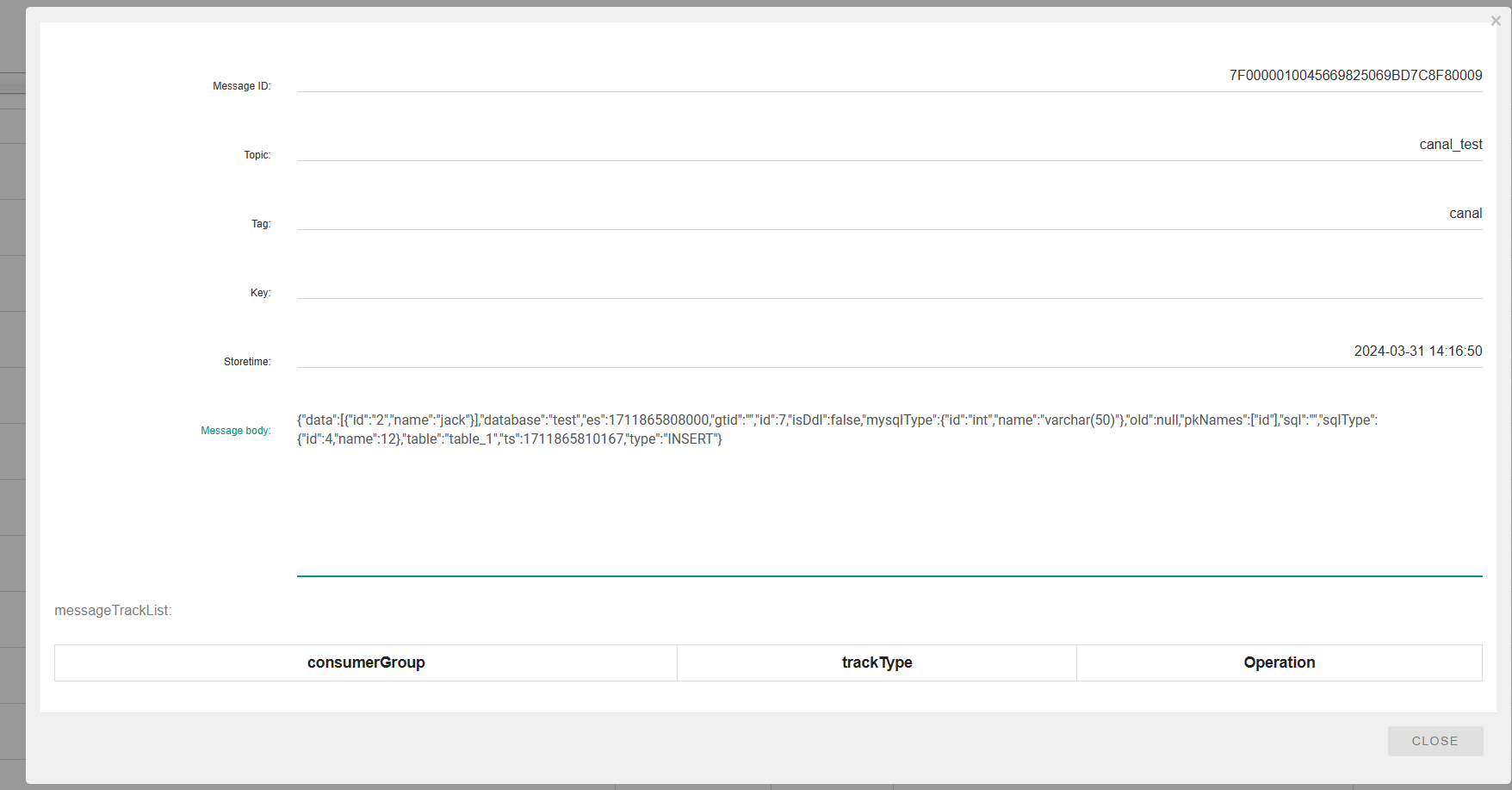
k8s 部署 canal 集群,RocketMQ 模式
k8s 部署 canal 集群,RocketMQ 模式 k8s 部署 canal 集群,RocketMQ 模式前提MySQLRocketMQ制作 canal-admin、canal-server 镜像 部署 zookeeper部署 canal-admin部署 canal-server测试 k8s 部署 canal 集群,RocketMQ 模式 前提 MySQL 开启…...

Android+OnnxRuntime+Opencv+Onnx模型操作图片擦除多余内容
今年来AI的发展非常迅速,在工业、医疗等等行业逐渐出现相应的解决方案,AI也逐渐成为各行业基础设施建设重要的一环,未来发展的大趋势,不过这也需要一个漫长的过程,需要很多技术型人才加入其中,除了工业设施的基础建设,在娱乐方向也有很多有趣的能力,不如图片/视频换背景…...

【CANoe】CAPL_E2E测试-验证报文中的CRC值是否正确
文章目录 一、背景二、CRC校验算法实现_dll制作三、CAPL脚本编写四、测试结果4.1、Write输出窗口4.2、测试报告截图一、背景 在嵌入式软件开发过程中,对于一些报文,需要实现安全发送与安全接收,这就涉及到CRC和RollingCounter。整车和MCU通讯的报文需要对方进行校验才能正确…...

Linux云计算之网络基础8——IPV6和常用网络服务
目录 一、IPV6基础 IPV6详解 IPv6数据报的基本首部 IPv6数据报的扩展首部 IPv6地址的表示方法 IPv6地址分类 网际控制报文协议ICMPv6 二、cisco基于IPV6的配置 cisco基于IPV6的配置步骤 模拟配置 三、HTML基础介绍 文档的结构 动手操作一下 四、常用网络服务介绍…...

页面刚加载的时候显示自己定义的{{***}}然后一闪而过
这时候别用插值表达式语法了,直接用v-text或者v-html就能解决这个问题 但是有个问题,如下图所示: 具体bind使用方式,如下图所示: 但是v-bind也可以进行简写,就是去掉v-bind,直接写:…...
python批量转化pdf图片为jpg图片
1.把pdf图片批量转为jpg;需要注意的是,需要先安装poppler这个软件,具体安装教程放在下面代码中了 2.代码 #poppler安装教程参考:https://blog.csdn.net/wy01415/article/details/110257130 #windows上poppler下载链接:…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
