【NC50937】货仓选址
题目
货仓选址
二分,前缀和,数学推导
思路
由题意可知货仓的位置是可以和商店的位置重合的。首先应该将商店的坐标从小到大排序,然后假设商店的坐标为 a i a_i ai,货仓的坐标为 x x x,货仓左侧第一家商店(可能和货仓重合)的坐标为 a k a_k ak,则由题意计算出的距离应该为:
d i s t = ∑ i = 0 k ( x − a i ) + ∑ i = k + 1 n − 1 ( a i − x ) = ( k + 1 ) x − ∑ i = 0 k a i + ∑ i = k + 1 n − 1 a i − ( n − 1 − k ) x dist=\sum_{i=0}^k(x-a_i)+\sum_{i=k+1}^{n-1}(a_i-x)=(k+1)x-\sum_{i=0}^ka_i+\sum_{i=k+1}^{n-1}a_i-(n-1-k)x dist=i=0∑k(x−ai)+i=k+1∑n−1(ai−x)=(k+1)x−i=0∑kai+i=k+1∑n−1ai−(n−1−k)x
根据上面的推导最直观的思路就是枚举从 a 0 → a i a_0\to a_i a0→ai 的所有坐标,然后老老实实地计算每个 d i s t dist dist 取最小值,这种思路需要用到二分,具体见代码。
这里要记录的并不是像上面那样简单模拟的思路,而是更为巧妙一些的:
假设给出的商店坐标(排好序之后)为 1 , 2 , 6 , 9 1,2,6,9 1,2,6,9
则按上面模拟的思路计算可得:
| 货仓位置 | 距离 |
|---|---|
| 1 | 14 |
| 2 | 12 |
| 3 | 12 |
| 4 | 12 |
| 5 | 12 |
| 6 | 12 |
| 7 | 14 |
| 8 | 16 |
| 9 | 18 |
为什么不枚举小于 a 0 a_0 a0 和大于 a n a_n an 的位置呢?这个问题留给读者。
由上面的表格可以得出,似乎越往商店的中部位置靠近,距离就越短。
不妨直接研究中部的商店,这里的商店数是偶数个,则研究中间的两个商店,我们会得到一个有趣的结论:
在中部的两个商店之间建立货仓的话,各商店到货仓的距离是不变的,并且距离为两两对称的商店之间的距离之和,比如例子里面的距离就是 6 − 2 + 9 − 1 = 12 6-2+9-1=12 6−2+9−1=12。
所以这题可以直接求两两对称商店的距离之差的和即可,奇数个商店数就将货仓建立在最中间的商店处即可。具体的证明这里不做记录,但是是很容易想通的。
代码
代码一:二分模拟
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
typedef long long LL;int cmp(const void* a, const void* b) { return *(int*)a - *(int*)b; }// 寻找第一个小于等于 target 的元素的下标,没有则返回 -1
int first_le(int* arr, int n, int target) {int l = 0, r = n - 1, mid = 0;while (l <= r) {mid = l + ((r - l) >> 1);if (arr[mid] <= target) {if (mid == n - 1 || arr[mid + 1] > target) {return mid;}l = mid + 1;} else {r = mid - 1;}}return -1;
}int main(void) {int n = 0;scanf("%d", &n);int a[n], i = 0;for (i = 0; i < n; i++) {scanf("%d", a + i);}qsort(a, n, sizeof(int), cmp);LL sum[n], ans = LLONG_MAX, t = 0;sum[0] = a[0];for (i = 1; i < n; i++) {sum[i] = sum[i - 1] + a[i];}for (LL x = a[0]; x <= a[n - 1]; x++) {i = first_le(a, n, x);t = (i + 1) * x - sum[i] + sum[n - 1] - sum[i] - (n - 1 - i) * x;if (t < ans) ans = t;}printf("%lld\n", ans);return 0;
}
代码二:数学推导
#include <stdio.h>
#include <stdlib.h>#define N 1000005typedef long long LL;int cmp(const void* a, const void* b) { return *(int*)a - *(int*)b; }int main(void) {int n = 0;scanf("%d", &n);int a[n], i = 0;LL ans = 0;for (i = 0; i < n; i++) {scanf("%d", a + i);}qsort(a, n, sizeof(int), cmp);for (i = n >> 1; i < n; i++) {ans += a[i] - a[n - i - 1];}printf("%lld\n", ans);return 0;
}
相关文章:

【NC50937】货仓选址
题目 货仓选址 二分,前缀和,数学推导 思路 由题意可知货仓的位置是可以和商店的位置重合的。首先应该将商店的坐标从小到大排序,然后假设商店的坐标为 a i a_i ai,货仓的坐标为 x x x,货仓左侧第一家商店&#x…...

Nginx配置使用笔记
Nginx配置使用笔记 前言 官网下载压缩包https://nginx.org/ 解压完成后当前目录cmd输入nginx指令启动 访问http://localhost:80确认启动成功 1.部署前端项目 部署前端项目到路径E:\Workspaces\Vscode\app-web 2.0配置nginx.conf文件 在nginx安装的conf目录下新建一个文件夹l…...
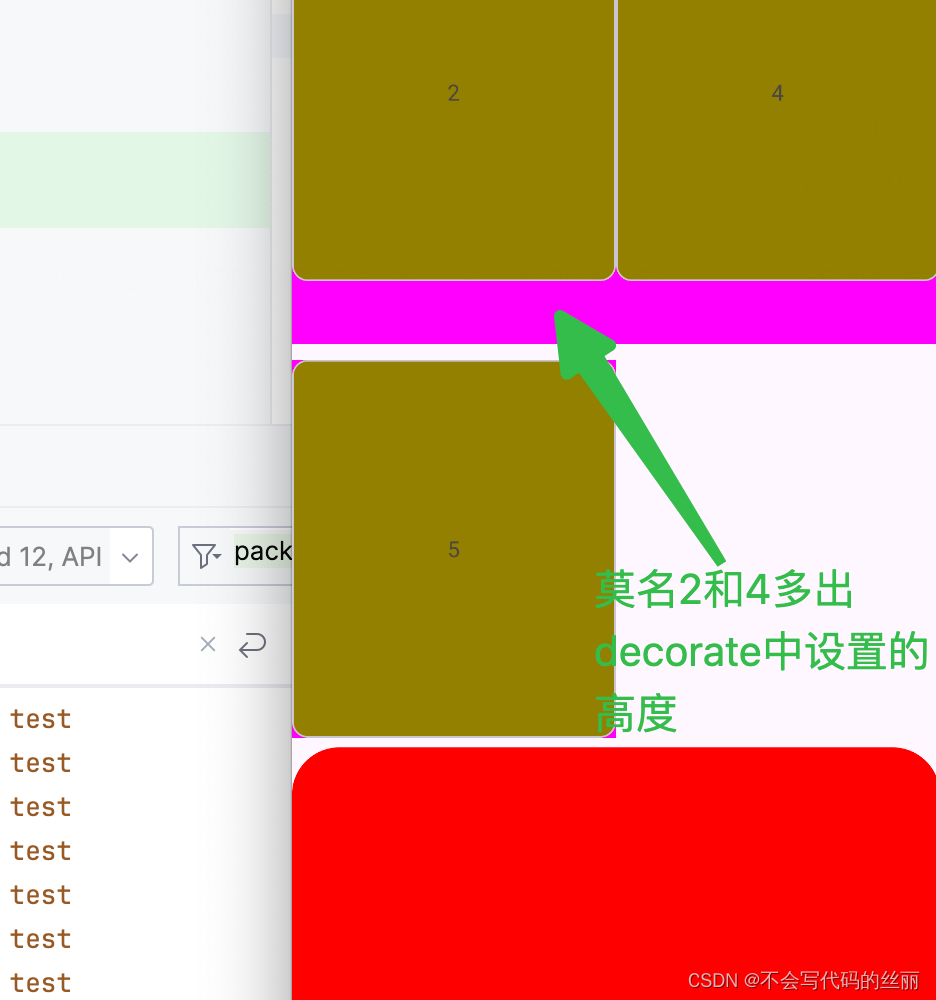
GridLayoutManager 中的一些坑
前言 如果GridLayoutManager使用item的布局都是wrap_cotent 那么会在布局更改时会出现一些出人意料的情况。(本文完全不具备可读性和说教性,仅为博主方便查找问题) 布局item: <!--layout_item.xml--> <?xml version"1.0&qu…...

算法实验二 矩阵最小路径和 LIS
算法实验课二 矩阵最小路径和 leetcode裸题 最小路径和 给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 示例 1: 输入&…...
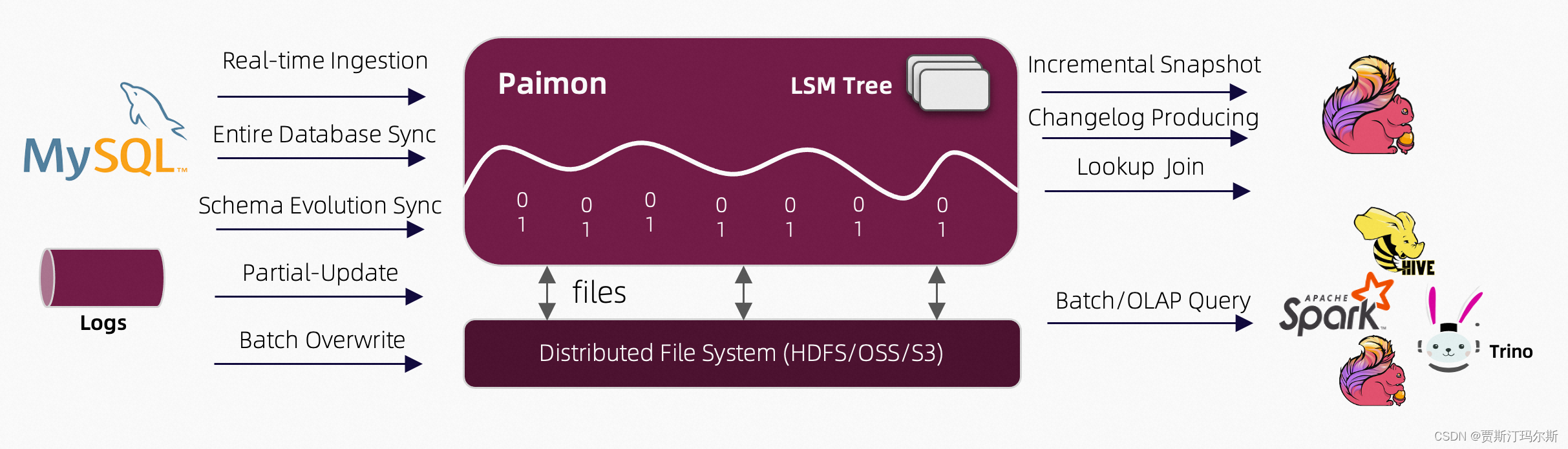
Apache Paimon实时数据糊介绍
Apache Paimon 是一种湖格式,可以使用 Flink 和 Spark 构建实时 数据糊 架构,用于流式和批处理操作。Paimon 创新地将湖格式和 LSM(日志结构合并树)结构相结合,将实时流式更新引入湖架构中。 Paimon 提供以下核心功能: 实时更新: 主键表支持大规模更新的写入,具有非常…...
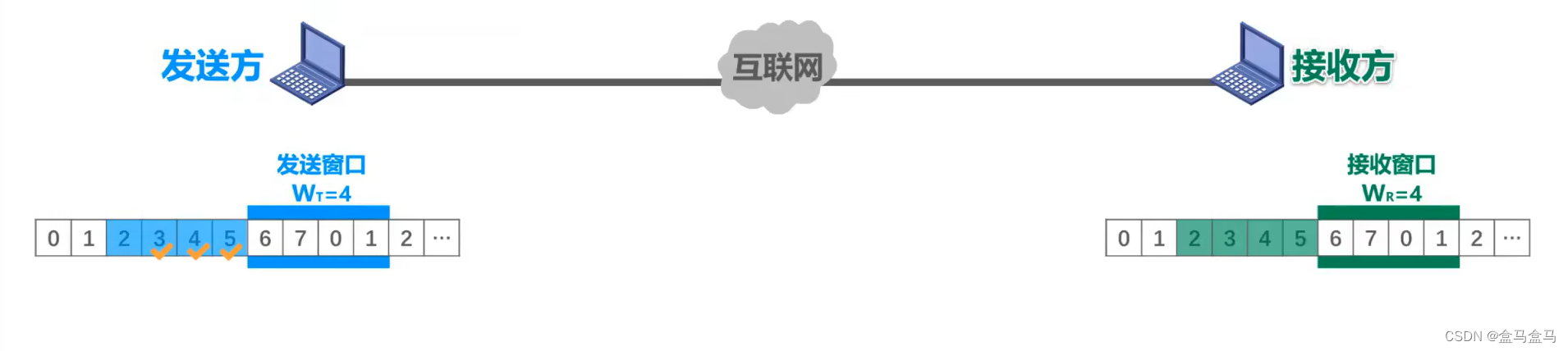
计算机网络:数据链路层 - 可靠传输协议
计算机网络:数据链路层 - 可靠传输协议 可靠传输概念停止-等待协议 SW回退N帧协议 GBN选择重传协议 SR 可靠传输概念 如下所示,帧在传输过程中受到干扰,产生了误码。接收方的数据链路层,通过真伪中的真检验序列 FCS 字段的值&…...

苍穹外卖07(缓存菜品,SpringCache,缓存套餐,添加购物车菜品和套餐多下单,查看购物车,清除购物车,删除购物车中一个商品)
目录 一、缓存菜品 1 问题说明 2 实现思路 3 代码开发:修改DishServiceImpl 4 功能测试 二、SpringCache 1. 介绍 2. 使用语法 1 起步依赖 2 使用要求 3 常用注解 4 SpEL表达式(了解备用) 5 步骤小结 3.入门案例 1 准备环境 2 使用入门 1 引导类上加…...

C语言第三十八弹---编译和链接
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 编译和链接 1、翻译环境和运行环境 2、翻译环境 2.1、预处理(预编译) 2.2、编译 2.2.1、词法分析 2.2.2、语法分析 2.2.3、语义分…...

无人售货奶柜:开启便捷生活的新篇章
无人售货奶柜:开启便捷生活的新篇章 在这个快节奏的现代生活中,科技的革新不仅为我们带来了前所未有的便利,更在不经意间改变着我们的日常。其中,无人售货技术的出现,尤其是无人售货奶柜,已经成为我们生活…...

STM32为什么不能跑Linux?
STM32是一系列基于ARM Cortex-M微控制器的产品,它们主要用于嵌入式系统中。而Linux则是一个开源的类Unix操作系统,主要面向的是桌面电脑、服务器等资源丰富的计算机。虽然理论上可以将Linux移植到STM32上运行,但是由于两者之间存在着很多技术…...
—Dubbo服务引用源码(1))
Dubbo 3.x源码(18)—Dubbo服务引用源码(1)
基于Dubbo 3.1,详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了Dubbo的服务导出的源码,在DubboBootstrapApplicationListener#startSync方法中,在调用了exportServices方法进行服务导出之后,立即调用了referServices方法…...

设计模式:工厂模式和抽象工厂模式的区别
定义 工厂模式(Factory Pattern)通常指的是工厂方法模式(Factory Method Pattern),它定义了一个创建对象的方法,由子类决定要实例化的类。工厂方法让类的实例化推迟到子类。 抽象工厂模式(Abstract Factory Pattern)提供了一个接口,用于创建相关或依赖对象的家族,而…...
)
python面试题(36~50)
36、如何取一个整数的绝对值? 这可以通过abs函数来实现。 abs(2) #> 2 abs(-2) #> 2 37、如何将两个列表组合成一个元组列表? 可以使用zip函数将列表组合成一个元组列表。这不仅仅限于使用两个列表。也适合3个或更多列表的情况。 a [a,b,c] b [1,2,3] [(k,v) fo…...
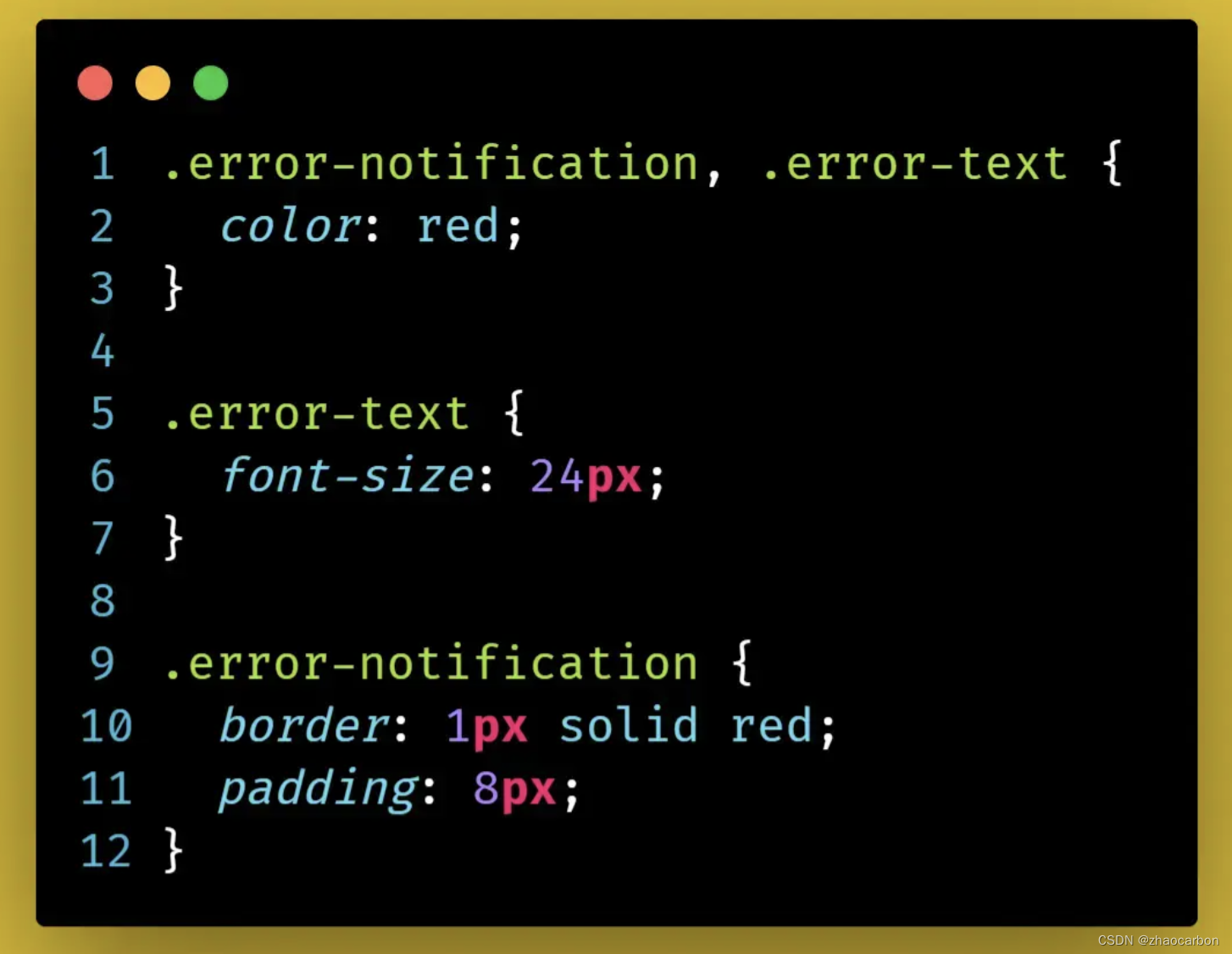
Vue 样式技巧总结与整理[中级局]
SFC(单文件组件)由 3 个不同的实体组成:模板、脚本和样式。三者都很重要,但后者往往被忽视,即使它可能变得复杂,且经常导致挫折和 bug。 更好的理解可以改善代码审查并减少调试时间。 这里有 7 个奇技淫巧…...
cesium加载.tif格式文件
最近项目中有需要直接加载三方给的后缀名tif格式的文件 <script src"https://cdn.jsdelivr.net/npm/geotiff"></script> 或者 yarn add geotiff npm install geotiff 新建tifs.js import GeoTIFF, { fromBlob, fromUrl, fromArrayBuffer } from geotif…...
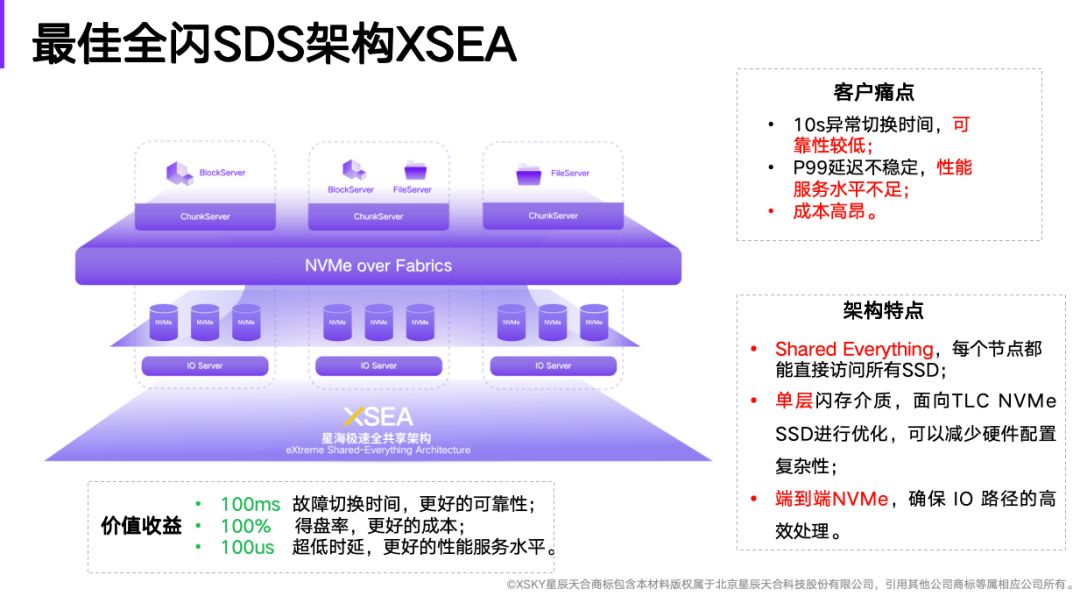
分布式全闪占比剧增 152%,2023 年企业存储市场报告发布
近日,IDC 发布了 2023 年度的中国存储市场报告。根据该报告,在 2023 年软件定义存储的市场占比进一步扩大,分布式全闪的增长尤其亮眼,其市场份额从 2022 年的 7% 剧增到 2023 年的 17.7%,增长了 152%。 01 中国企业存…...
双链表 模板))
LeetCode 707. 设计链表(单链表、(非循环)双链表 模板)
你可以选择使用单链表或者双链表,设计并实现自己的链表。 单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。 如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点…...

深入了解Flutter中Overlay的介绍以及使用
Flutter Overlay 介绍 在 Flutter 中,Overlay 是一种特殊的 Widget,它可以用来在应用程序的其他部分之上显示内容。Overlay 非常适合用于显示模态对话框、弹出菜单、工具提示等。 Overlay 的工作原理 Overlay 位于 Flutter 的渲染树之外,这…...

文本直接生成2分钟视频,即将开源模型StreamingT2V
Picsart人工智能研究所、德克萨斯大学和SHI实验室的研究人员联合推出了StreamingT2V视频模型。通过文本就能直接生成2分钟、1分钟等不同时间,动作一致、连贯、没有卡顿的高质量视频。 虽然StreamingT2V在视频质量、多元化等还无法与Sora媲美,但在高速运…...

时序预测 | Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测
时序预测 | Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测 目录 时序预测 | Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现SOM-BP自组织映射结合BP神经网络时间序列预测(完整源码…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
