静态成员主要用于提供与类本身相关的功能或数据,有什么应用场景
静态成员(包括静态方法和静态属性)在JavaScript中常用于多种应用场景,它们为类提供了与类本身直接相关而不是与实例相关的功能或数据。以下是一些常见的应用场景:
工厂方法
静态方法可以作为工厂方法,用于创建类的实例。这种方法的好处是,它不需要实例化类就可以调用,因此可以在不改变类状态的情况下创建对象。
javascript复制代码
class User { | |
constructor(name, age) { | |
this.name = name; | |
this.age = age; | |
} | |
static createUser(name, age) { | |
return new User(name, age); | |
} | |
} | |
const user = User.createUser('Alice', 30); |
工具函数
静态方法经常用作工具函数,这些函数与类实例的状态无关,而是提供某种通用的功能。
javascript复制代码
class MathUtils { | |
static sum(a, b) { | |
return a + b; | |
} | |
static multiply(a, b) { | |
return a * b; | |
} | |
} | |
const result = MathUtils.sum(2, 3); // 调用静态方法 |
配置或常量
静态属性常用于存储配置信息或常量值,这些值对类的所有实例都是相同的。
javascript复制代码
class AppConfig { | |
static API_URL = 'https://api.example.com'; | |
static VERSION = '1.0.0'; | |
} | |
console.log(AppConfig.API_URL); // 输出配置的API URL |
单例模式
静态成员可以用于实现单例模式,确保一个类只有一个实例,并提供一个全局访问点。
javascript复制代码
class Singleton { | |
static instance = null; | |
static getInstance() { | |
if (!Singleton.instance) { | |
Singleton.instance = new Singleton(); | |
} | |
return Singleton.instance; | |
} | |
// 私有构造函数,防止直接实例化 | |
private constructor() { | |
// 初始化代码... | |
} | |
} | |
const instance1 = Singleton.getInstance(); | |
const instance2 = Singleton.getInstance(); | |
console.log(instance1 === instance2); // 输出: true,证明两个引用指向同一个实例 |
类级别的状态
尽管不常见,但有时可能需要在类级别维护一些状态,而不是在实例级别。这可以通过静态属性来实现。
javascript复制代码
class Counter { | |
static count = 0; | |
static increment() { | |
Counter.count++; | |
} | |
static getCount() { | |
return Counter.count; | |
} | |
} | |
Counter.increment(); | |
Counter.increment(); | |
console.log(Counter.getCount()); // 输出: 2 |
在以上场景中,静态成员提供了一种将数据和功能与类本身关联起来的方式,而不是与类的特定实例关联。这有助于组织代码,提高代码的可读性和可维护性,并允许在不需要实例化类的情况下执行操作。
相关文章:

静态成员主要用于提供与类本身相关的功能或数据,有什么应用场景
静态成员(包括静态方法和静态属性)在JavaScript中常用于多种应用场景,它们为类提供了与类本身直接相关而不是与实例相关的功能或数据。以下是一些常见的应用场景: 工厂方法 静态方法可以作为工厂方法,用于创建类的实…...

在线考试|基于Springboot的在线考试管理系统设计与实现(源码+数据库+文档)
在线考试管理系统目录 目录 基于Springboot的在线考试管理系统设计与实现 一、前言 二、系统设计 三、系统功能设计 1、前台: 2、后台 管理员功能 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: 博主…...

C语言-----数据在内存中的存储(1)
1.整数在内存中的存储 我们之前就了解过整数的二进制写法分别有3种,分别为原码,反码,补码。整型在内存中存储的是补码。 原码,反码,补码都有自己的符号位和数值位,符号位为1时,则表示负数&…...
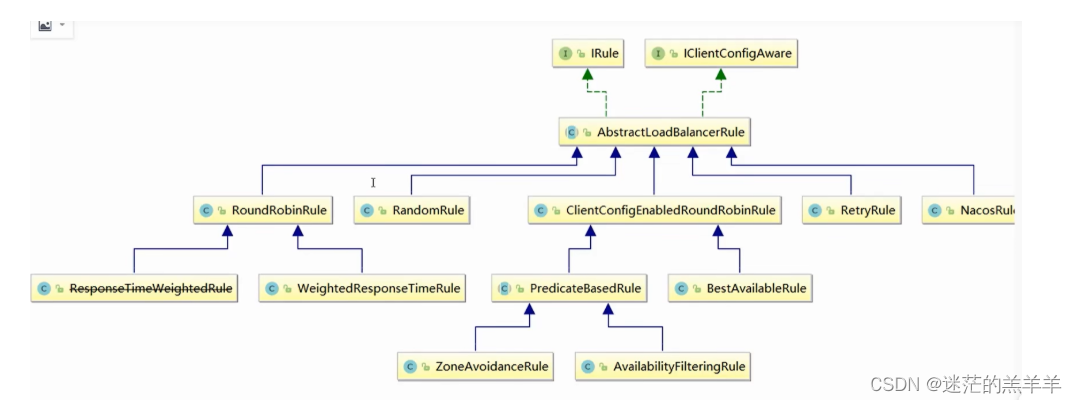
Ribbon有哪些负载均衡策略
负载均衡类都实现了IRule接口。 RandomRule:随机的选用一个实例 RoundRobinRule:轮询的使用实例 RetryRule:在轮询的基础上加了一个错误重试机制,在deadline时间内会不断的重试 WeightResponeTimeRule:根据权重去做…...

websocket多级nginx代理
在使用多层Nginx代理时,WebSocket的连接可能会遇到一些问题,因为WebSocket连接是持久化的,它需要Upgrade头部来确认升级到WebSocket协议。在多层代理的情况下,每层代理可能会修改或丢失这个Upgrade头部信息。 为了确保WebSocket能…...
【python从入门到精通】-- 第四战:语句汇总
🌈 个人主页:白子寰 🔥 分类专栏:python从入门到精通,魔法指针,进阶C,C语言,C语言题集,C语言实现游戏👈 希望得到您的订阅和支持~ 💡 坚持创作博文…...

【NC50937】货仓选址
题目 货仓选址 二分,前缀和,数学推导 思路 由题意可知货仓的位置是可以和商店的位置重合的。首先应该将商店的坐标从小到大排序,然后假设商店的坐标为 a i a_i ai,货仓的坐标为 x x x,货仓左侧第一家商店&#x…...

Nginx配置使用笔记
Nginx配置使用笔记 前言 官网下载压缩包https://nginx.org/ 解压完成后当前目录cmd输入nginx指令启动 访问http://localhost:80确认启动成功 1.部署前端项目 部署前端项目到路径E:\Workspaces\Vscode\app-web 2.0配置nginx.conf文件 在nginx安装的conf目录下新建一个文件夹l…...
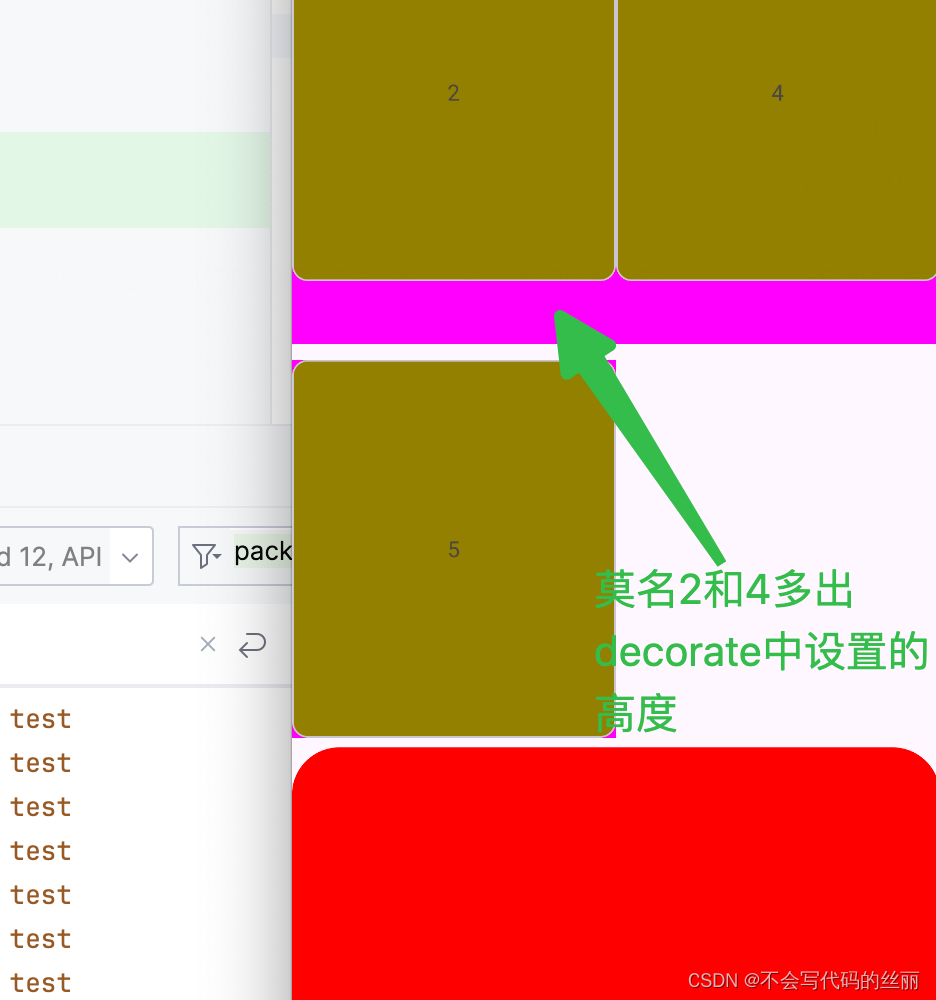
GridLayoutManager 中的一些坑
前言 如果GridLayoutManager使用item的布局都是wrap_cotent 那么会在布局更改时会出现一些出人意料的情况。(本文完全不具备可读性和说教性,仅为博主方便查找问题) 布局item: <!--layout_item.xml--> <?xml version"1.0&qu…...

算法实验二 矩阵最小路径和 LIS
算法实验课二 矩阵最小路径和 leetcode裸题 最小路径和 给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 示例 1: 输入&…...
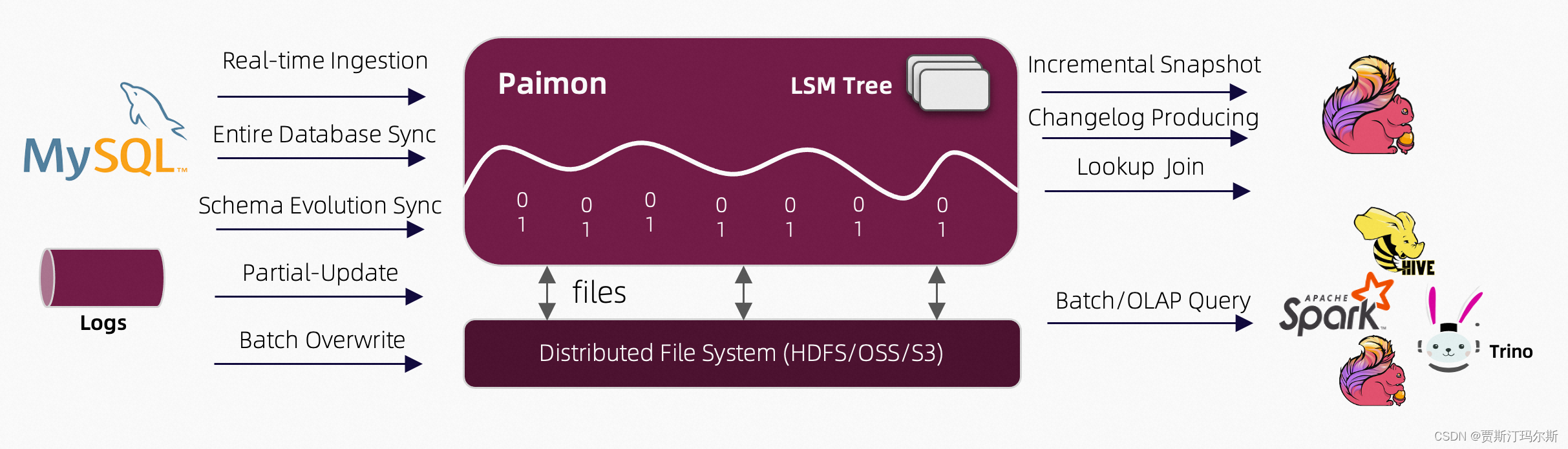
Apache Paimon实时数据糊介绍
Apache Paimon 是一种湖格式,可以使用 Flink 和 Spark 构建实时 数据糊 架构,用于流式和批处理操作。Paimon 创新地将湖格式和 LSM(日志结构合并树)结构相结合,将实时流式更新引入湖架构中。 Paimon 提供以下核心功能: 实时更新: 主键表支持大规模更新的写入,具有非常…...
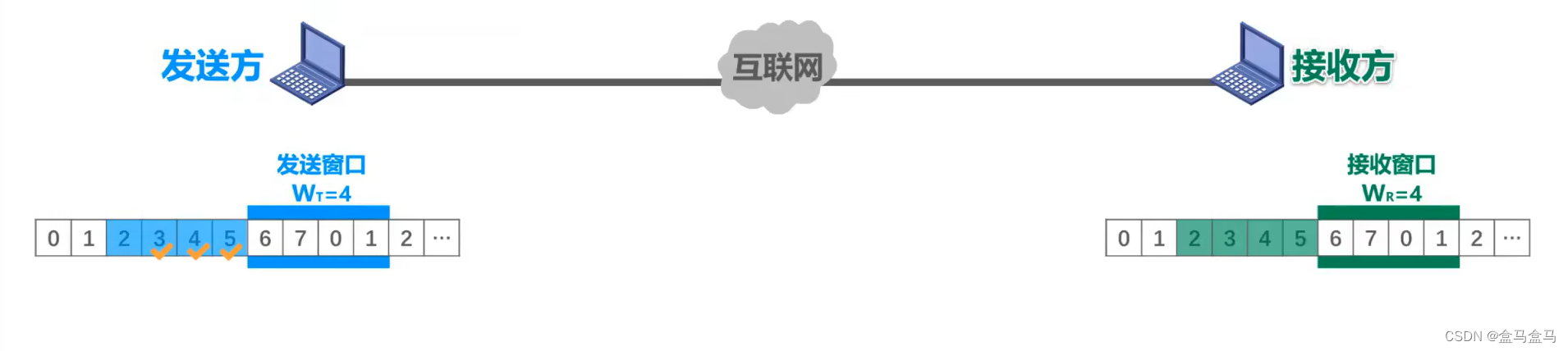
计算机网络:数据链路层 - 可靠传输协议
计算机网络:数据链路层 - 可靠传输协议 可靠传输概念停止-等待协议 SW回退N帧协议 GBN选择重传协议 SR 可靠传输概念 如下所示,帧在传输过程中受到干扰,产生了误码。接收方的数据链路层,通过真伪中的真检验序列 FCS 字段的值&…...

苍穹外卖07(缓存菜品,SpringCache,缓存套餐,添加购物车菜品和套餐多下单,查看购物车,清除购物车,删除购物车中一个商品)
目录 一、缓存菜品 1 问题说明 2 实现思路 3 代码开发:修改DishServiceImpl 4 功能测试 二、SpringCache 1. 介绍 2. 使用语法 1 起步依赖 2 使用要求 3 常用注解 4 SpEL表达式(了解备用) 5 步骤小结 3.入门案例 1 准备环境 2 使用入门 1 引导类上加…...

C语言第三十八弹---编译和链接
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 编译和链接 1、翻译环境和运行环境 2、翻译环境 2.1、预处理(预编译) 2.2、编译 2.2.1、词法分析 2.2.2、语法分析 2.2.3、语义分…...

无人售货奶柜:开启便捷生活的新篇章
无人售货奶柜:开启便捷生活的新篇章 在这个快节奏的现代生活中,科技的革新不仅为我们带来了前所未有的便利,更在不经意间改变着我们的日常。其中,无人售货技术的出现,尤其是无人售货奶柜,已经成为我们生活…...

STM32为什么不能跑Linux?
STM32是一系列基于ARM Cortex-M微控制器的产品,它们主要用于嵌入式系统中。而Linux则是一个开源的类Unix操作系统,主要面向的是桌面电脑、服务器等资源丰富的计算机。虽然理论上可以将Linux移植到STM32上运行,但是由于两者之间存在着很多技术…...
—Dubbo服务引用源码(1))
Dubbo 3.x源码(18)—Dubbo服务引用源码(1)
基于Dubbo 3.1,详细介绍了Dubbo服务的发布与引用的源码。 此前我们学习了Dubbo的服务导出的源码,在DubboBootstrapApplicationListener#startSync方法中,在调用了exportServices方法进行服务导出之后,立即调用了referServices方法…...

设计模式:工厂模式和抽象工厂模式的区别
定义 工厂模式(Factory Pattern)通常指的是工厂方法模式(Factory Method Pattern),它定义了一个创建对象的方法,由子类决定要实例化的类。工厂方法让类的实例化推迟到子类。 抽象工厂模式(Abstract Factory Pattern)提供了一个接口,用于创建相关或依赖对象的家族,而…...
)
python面试题(36~50)
36、如何取一个整数的绝对值? 这可以通过abs函数来实现。 abs(2) #> 2 abs(-2) #> 2 37、如何将两个列表组合成一个元组列表? 可以使用zip函数将列表组合成一个元组列表。这不仅仅限于使用两个列表。也适合3个或更多列表的情况。 a [a,b,c] b [1,2,3] [(k,v) fo…...
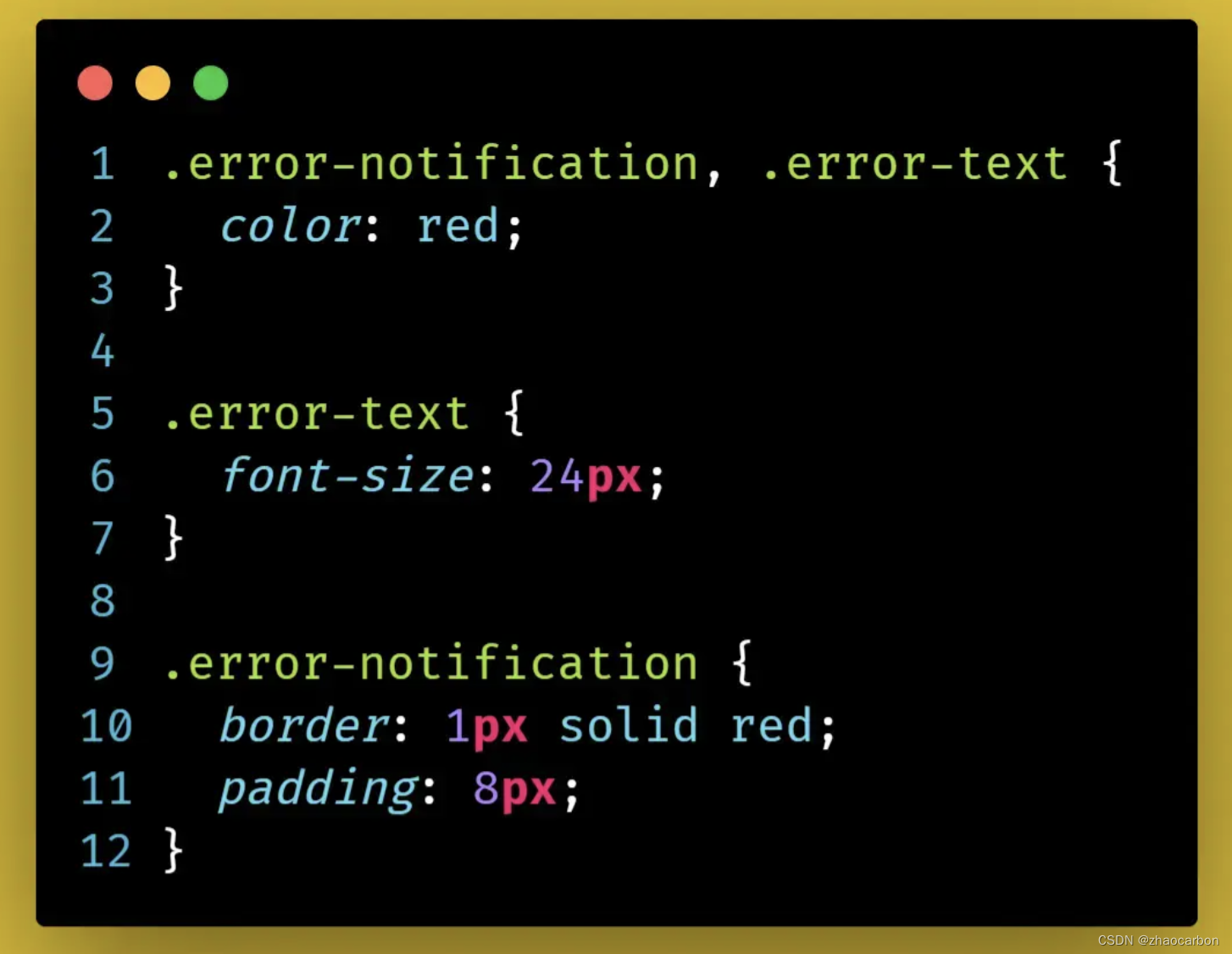
Vue 样式技巧总结与整理[中级局]
SFC(单文件组件)由 3 个不同的实体组成:模板、脚本和样式。三者都很重要,但后者往往被忽视,即使它可能变得复杂,且经常导致挫折和 bug。 更好的理解可以改善代码审查并减少调试时间。 这里有 7 个奇技淫巧…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
