数据结构刷题(十九):77组合、216组合总和III
1.组合
题目链接
过程图:先从集合中取一个数,再依次从剩余数中取k-1个数。
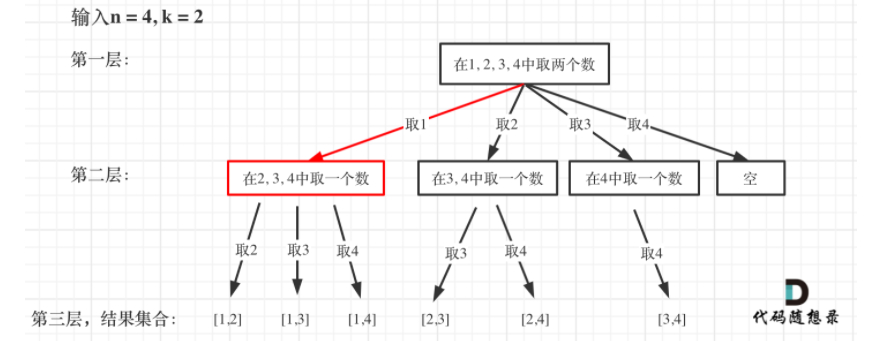
思路:回溯算法。使用回溯三部曲进行解题:
递归函数的返回值以及参数:n,k,startIndex(记录每次循环集合从哪里开始遍历的位置),其中startIndex 就是防止出现重复的组合。比如从1开始了循环,则使用startindex=2,让startindex作为下次循环的开始。
还有全局变量:一个是用来存放一个符合条件的结果path,一个用来存放所有符合条件的结果集合result。
回溯函数终止条件:path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合,在图中path存的就是根节点到叶子节点的路径
单层搜索的过程:for循环用来横向遍历,递归的过程是纵向遍历。
(1)for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
(2)递归函数不断调用自己往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
(3)递归函数下面部分就是回溯的操作了,撤销本次处理的结果。
最终结果代码:
class Solution {// 存放单个结果path, 存放所有结果resList<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {combineHelper(n, k, 1);return res;}// startindex就是循环开始位置private void combineHelper(int n, int k, int startindex) {// 终止条件 if (path.size() == k){res.add(new ArrayList<>(path));return;}// 单层逻辑for (int i = startindex; i <= n ; i++ ){path.add(i);combineHelper(n, k, i + 1);path.removeLast();}}
}剪枝优化:
(1)假设n = 4,k = 4,就四个数,还求四个数的组合,那必然只有一个组合,从2开始for循环再找其他数没有意义。所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置,在循环中i就是循环的起始位置。也就是说for循环的开始位置到结束位置一共的元素个数<k时,就不需要判断了。
(2)过程:
已经选择的元素个数:path.size();
还需要的元素个数为: k - path.size();
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历。也就是说 n - (k - path.size()) + 1是最晚的起始位置,如果超过了这个位置找元素,path的元素个数不可能到达k个。这里面+1是闭区间的意思。
最终优化后的代码:
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {combineHelper(n, k, 1);return res;
}private void combineHelper(int n, int k, int startindex) {if (path.size() == k){res.add(new ArrayList<>(path));return;}for (int i = startindex; i <= n - (k - path.size()) + 1; i++ ){path.add(i);combineHelper(n, k, i + 1);path.removeLast();}
}2.组合总和III
题目链接
过程图:和上一题组合类似,仍然是先取某个值,然后再从其他数中k-1个进行组合。
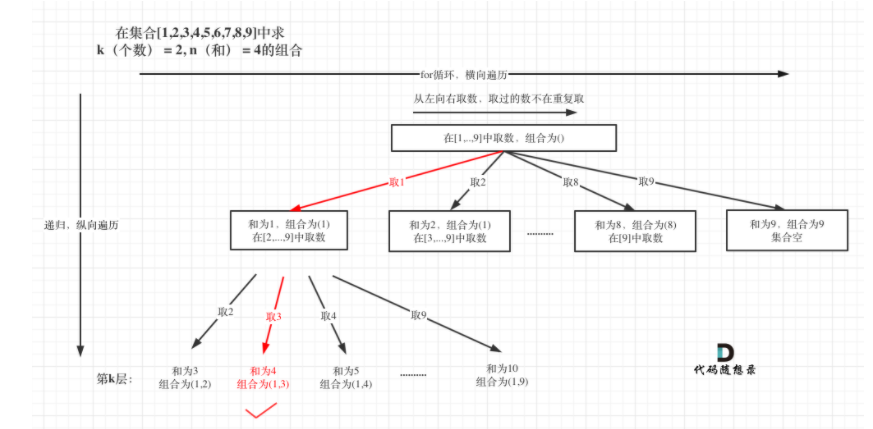
思路:回溯三部曲。
确定递归函数参数:题目中的n和k,sum(已经收集的元素的总和也就是path里元素的总和),startIndex为下一层for循环搜索的起始位置。
确定终止条件:path.size() 和 k相等且sum=n
单层搜索过程: path收集每次选取的元素,sum来统计path里元素的总和。别忘了回溯。
3.代码:
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum3(int k, int n) {backTracking(n, k, 1, 0);return result;}// targetSum就是n, sum是和private void backTracking(int targetSum, int k, int startIndex, int sum) {// 减枝if (sum > targetSum) {return;}if (path.size() == k) {if (sum == targetSum) result.add(new ArrayList<>(path));return;}// 减枝 9 - (k - path.size()) + 1for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {path.add(i);sum += i;backTracking(targetSum, k, i + 1, sum);//回溯path.removeLast();//回溯sum -= i;}}
}相关文章:

数据结构刷题(十九):77组合、216组合总和III
1.组合题目链接过程图:先从集合中取一个数,再依次从剩余数中取k-1个数。思路:回溯算法。使用回溯三部曲进行解题:递归函数的返回值以及参数:n,k,startIndex(记录每次循环集合从哪里开始遍历的位…...
PyQt 做美*女GIF设置桌面,每天都很爱~
人生苦短,我用python 要说程序员工作的最大压力不是来自于工作本身, 而是来自于需要不断学习才能更好地完成工作, 因为程序员工作中面对的编程语言是在不断更新的, 同时还要学习熟悉其他语言来提升竞争力… 好了,学习…...

[渗透测试笔记] 54.日薪2k的蓝队hw中级定级必备笔记系列篇3之域渗透黄金票据和白银票据
前文链接 [渗透测试笔记] 52.告别初级,日薪2k的蓝队hw中级定级必备笔记 [渗透测试笔记] 53.日薪2k的蓝队hw中级定级必备笔记2 文章目录 Kerberos认证协议NTLM认证协议Kerberos和NTLM比较黄金票据原理黄金票据条件复现过程白银票据原理白银票据条件复现过程黄金票据和白银票据…...

【异常】Spring Cloud Gateway网关自定义过滤器无法获取到请求体body的内容?不存在的!
一、需求说明 项目要使用到网关SpringCloud Gateway进行验签,现在定义了一个过滤器ValidateSignFilter, 我希望,所以过网关SpringCloud Gateway的请求,都能够校验一下请求头,看看是否有Sign这个字段放在请求头中。 二、异常说明 但是,我遇到了SpringCloud Gateway网关…...
)
CNN 卷积神经网络对染色血液细胞分类(blood-cells)
目录 1. 介绍 2. 加载数据 3. 可视化 3.1 显示单幅图像 3.2 显示多幅图像...
Kubernetes学习(三)Service
Service对象 为什么需要Service 每个Pod都有自己的IP地址,但是在Deployment中,在同一时刻运行的Pod集合可能与稍后运行该应用程序的Pod集合不同。 这就导致了一个问题:如果一组Pod(称为后端)为集群内其他Pod&#x…...
)
数学小课堂:古德-图灵折扣估计法和插值法(防范黑天鹅事件的方法)
文章目录 引言I 黑天鹅事件产生的原因1.1 置信度1.2 数据的稀疏性1.3 零概率问题II 防范黑天鹅事件的方法2.1 古德-图灵折扣估计法2.2 插值法引言 防范黑天鹅事件的方法 古德-图灵折扣估计法:它主要是解决零概率的事件古德的方法虽然解决了零概率的问题,但是依然没有解决数据…...

redis getshell方法
前言 参考文章 https://paper.seebug.org/1169 https://blog.csdn.net/weixin_55843787/article/details/123829606 https://blog.csdn.net/chenglanqi6606/article/details/100909518 Redis是什么 Redis是一款基于键值对的NoSQL数据库,它的值支持多种数据结构 …...
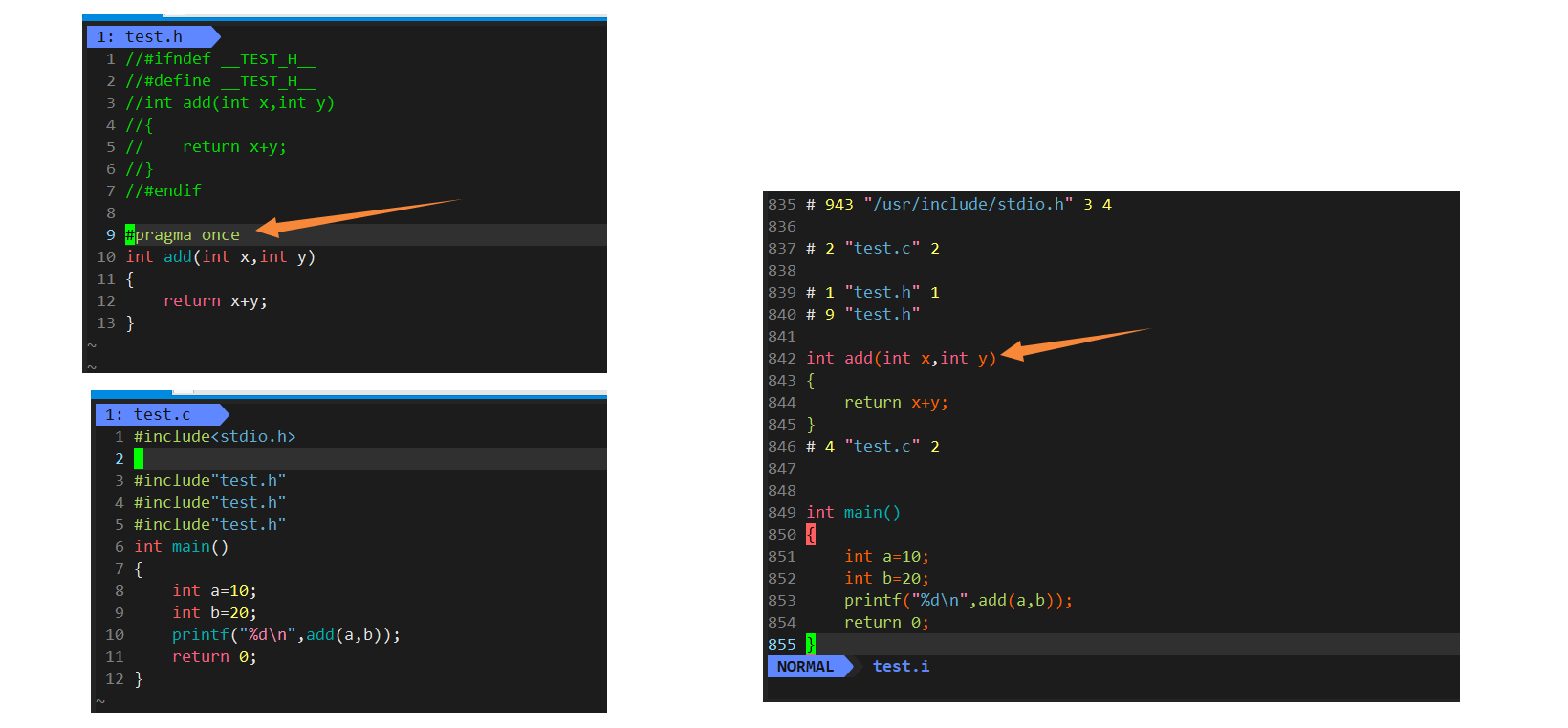
【ONE·C || 程序编译简述】
总言 C语言:程序编译相关。 文章目录总言1、程序的翻译环境和运行环境1.1、简述1.2、翻译环境:程序编译与链接1.2.1、简介:程序如何从.c文件形成.exe可执行程序1.2.2、过程说明1.3、运行环境2、预处理详解2.1、预定义符号2.2、#define2.…...

MGAT: Multimodal Graph Attention Network for Recommendation
模型总览如下: 图1:多模态图注意力网络背景:本论文是对MMGCN(Wei et al., 2019)的改进。MMGCN简单地在并行交互图上使用GNN,平等地对待从所有邻居传播的信息,无法自适应地捕获用户偏好。 MMGCN…...
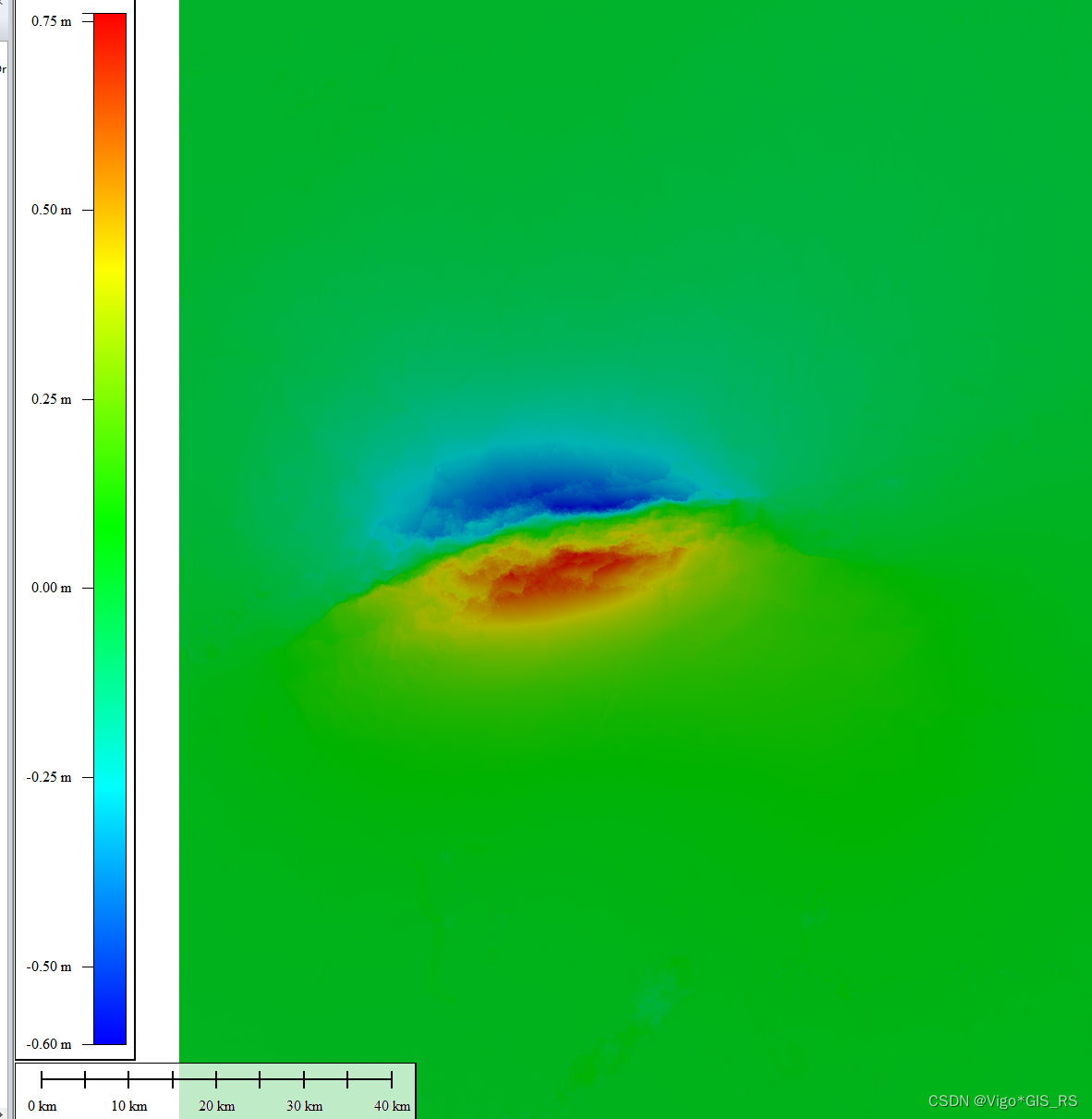
在SNAP中用sentinel-1数据做InSAR测量,以门源地震为例
在SNAP中用sentinel-1数据做InSAR0 写在前面1 数据下载2 处理步骤2.1 split2.2 apply orbit 导入精密轨道2.3 查看数据的时空基线base line2.4 back-geocoding 配准2.5 Enhanced Spectral Diversity2.6 Deburst2.7 Interogram Formation 生成干涉图2.8 Multilook 多视2.9 Golds…...
MySQL常用函数
什么是函数? 函数是指一段可以直接被另一段程序调用的程序或代码。 字符串函数 函数功能CONCAT(S1,S2,…Sn)字符串拼接,将S1,S2,… Sn拼接成一个字符串LOWER(str)将字符串str全部转为小写LOWER(str)将字符串str全部转为小写LPAD(…...

51单片机数字电子钟开题报告
目录 选题背景 初步设计方案 芯片的选型 编译环境 关键问题 策略 方案 参考文献 选题背景 数字电子钟是一种受到越来越多人喜爱的钟表,其准确性和稳定性成为设计和研发的重要考虑因素。在现代社会,时间的准确性对于各行各业都非常重要࿰…...

day7 HTTP协议
HTTP协议 什么是协议? 协议实际上是某些人,或者某些组织提前制定好的一套规范,大家都按照这个规范来,这样可以做到沟通无障碍。协议就是一套规范,就是一套标准。由其他人或其他组织来负责制定的。我说的话你能听懂&…...
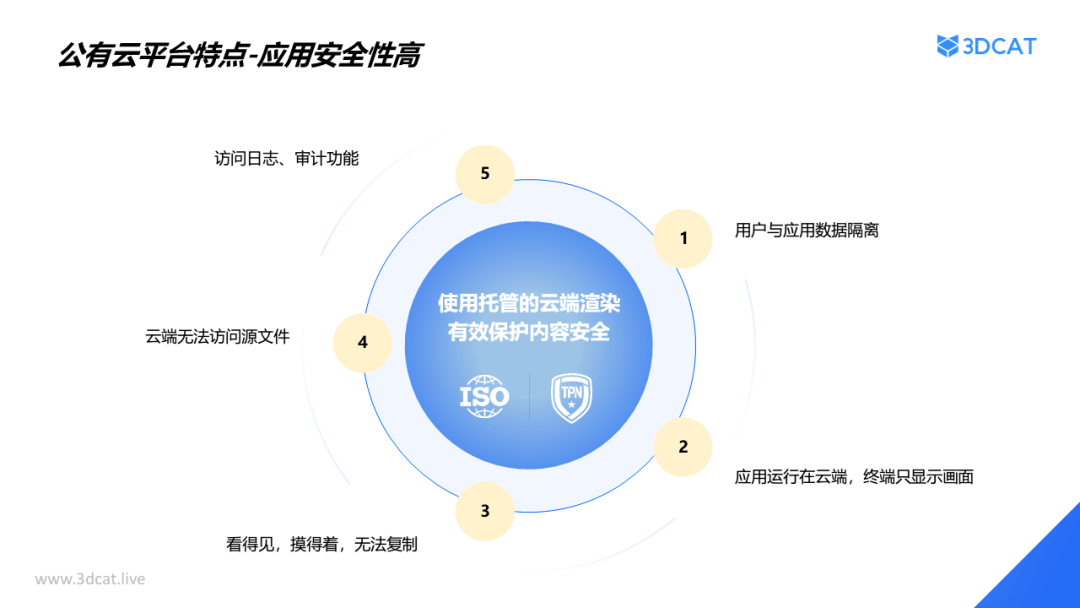
3DCAT+一汽奥迪:共建线上个性化订车实时云渲染方案
近年来,随着5G网络和云计算技术的不断发展,交互式3D实时云看车正在成为一种新的看车方式。与传统的到4S店实地考察不同,消费者可以足不出户,通过网络与终端设备即可实现全方位展示、自选汽车配色、模拟效果、快捷选车并进行个性化…...
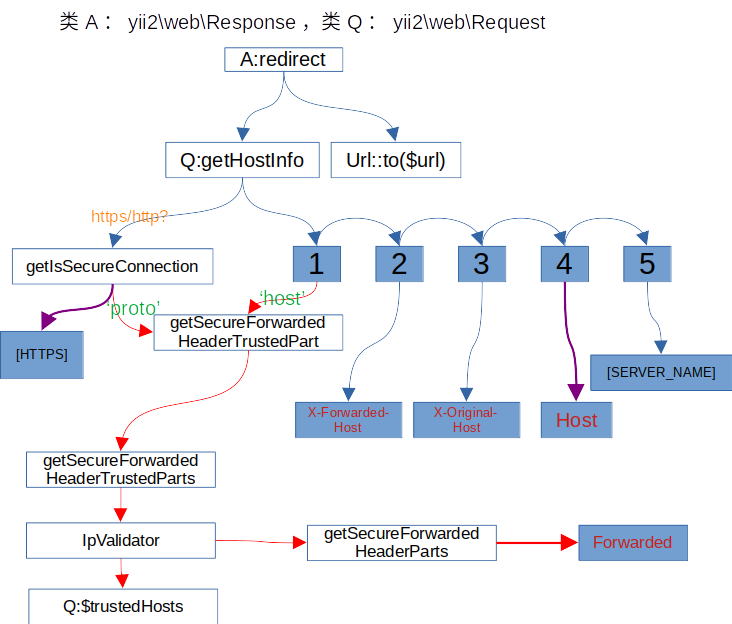
yii2项目使用frp https2http插件问题
yii2内网项目,使用frp进行内网穿透,使用 https2http插件把内网服务器http流量转成https,会存在一个问题:当使用 $this->redirect(...) 或 $this->goHome() (其实用的也是前者)等重定向时,…...

关于 interface{} 会有啥注意事项?下
我们一起来回顾一下上一次说到的 interface{} 可以用来做多态 接口类型分为空接口类型和非空接口类型,他们的底层数据结构不太一样 这里顺便说一下,用来作态需要满足这样的条件: 首先得有父类指针指向子类的对象这个接口还必须是非空接口…...
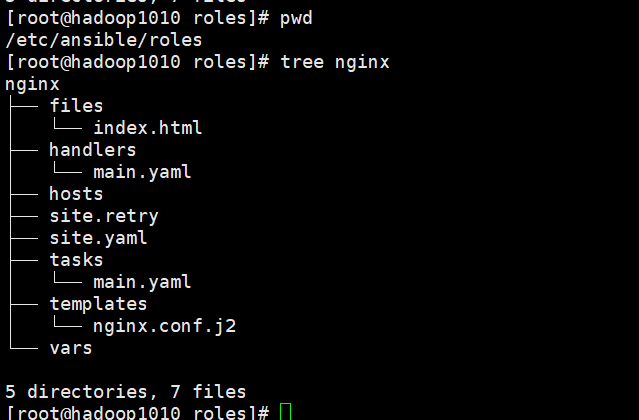
ansible组件介绍和简单playbook测试
一、ansible inventory 在大规模的配置管理工作中,管理不同业务的机器,机器的信息都存放在ansible的inventory组件里面。在工作中,配置部署针对的主机必须先存放在Inventory里面,然后ansible才能对它进行操作。默认的Ansible的in…...
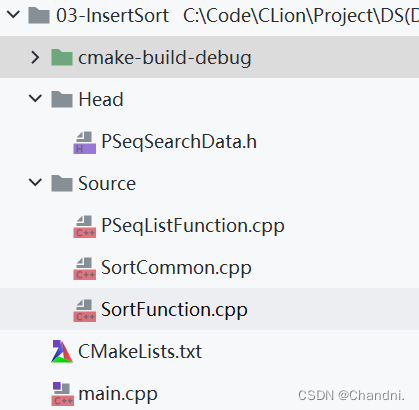
[数据结构]:13-插入排序(顺序表指针实现形式)(C语言实现)
目录 前言 已完成内容 插入排序实现 01-开发环境 02-文件布局 03-代码 01-主函数 02-头文件 03-PSeqListFunction.cpp 04-SortCommon.cpp 05-SortFunction.cpp 结语 前言 此专栏包含408考研数据结构全部内容,除其中使用到C引用外,全为C语言代…...
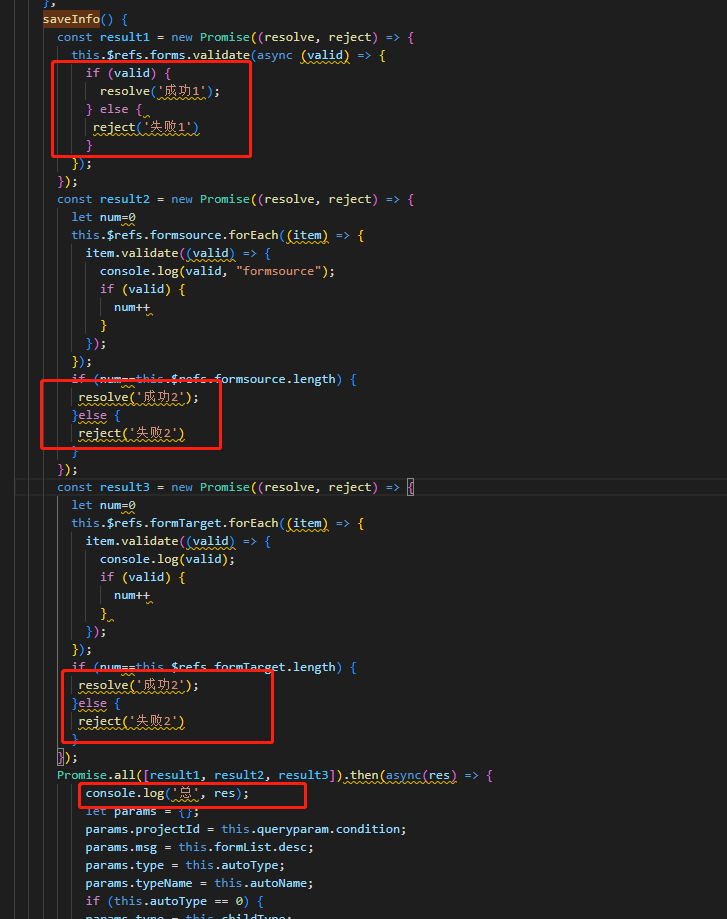
es6 new Promise
Promise 是一个构造函数,本身身上有 all、reject、resolve 这几个方法,原型上有 then、catch 等方法。所以 Promise new 出来的对象确定就有 then、catch 方法。Promise 的构造函数接收一个参数,是函数,而且传入两个参数ÿ…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
