剑指 Offer 43. 1~n 整数中 1 出现的次数
摘要
剑指 Offer 43. 1~n 整数中 1 出现的次数
一、数学思维解析
将1~ n的个位、十位、百位、...的1出现次数相加,即为1出现的总次数。
设数字n是个x位数,记n的第i位为ni,则可将n写为 nxnx−1⋯n2n1:
- 称" ni" 为 当前位 ,记为 cur ,
- 将" ni−1ni−2⋯n2n1 " 称为 低位 ,记为low ;
- 将" nxnx−1⋯ni+2ni+1 " 称为高位 ,记为high 。
- 将10i称为位因子 ,记为digit。
某位中1出现次数的计算方法:根据当前位 cur值的不同,分为以下三种情况:
当 cur=0时: 此位1的出现次数只由高位 high决定,计算公式为:high×digit:

当cur=1时: 此位1的出现次数由高位high和低位low决定,计算公式为:high×digit+low+1

当cur=2,3,⋯ ,9时: 此位1的出现次数只由高位 high决定,计算公式为:(high+1)×digit:

package Math;/*** @Classname JZ43整数中1出现的次数* @Description TODO* @Date 2023/3/7 20:55* @Created by xjl*/
public class JZ43整数中1出现的次数 {/*** @description 整数中1出现的次数 * @param: n* @date: 2023/3/7 20:56* @return: int* @author: xjl*/public int countDigitOne(int n) {int digit = 1, res = 0;int high = n / 10, cur = n % 10, low = 0;while (high != 0 || cur != 0) {if (cur == 0) {res += high * digit;} else if (cur == 1) {res += high * digit + low + 1;} else {res += (high + 1) * digit;}low += cur * digit;cur = high % 10;high /= 10;digit *= 10;}return res;}
}
复杂度分析:
- 时间复杂度O(logn): 循环内的计算操作使用O(1)时间;循环次数为数字n的位数,即log10n,因此循环使用O(logn)时间。
- 空间复杂度 O(1) : 几个变量使用常数大小的额外空间。
二、暴力解析
一般是超时的选择
/*** @description 相当于的暴力求解的顺序* @param: n* @date: 2023/3/7 21:15* @return: int* @author: xjl*/public int countDigitOne2(int n) {String result = "";for (int i = 1; i <= n; i++) {result += String.valueOf(i);}int count = 0;for (int i = 0; i < result.length(); i++) {if (result.charAt(i) == '1') {count++;}}return count;}复杂度分析:
- 时间复杂度O(n): 循环内的计算操作使用O(1)时间;循环次数为数字n的位数,即log10n,因此循环使用O(logn)时间。
- 空间复杂度 O(n) : 几个变量使用常数大小的额外空间。
博文参考
《leetcode》
相关文章:

剑指 Offer 43. 1~n 整数中 1 出现的次数
摘要 剑指 Offer 43. 1~n 整数中 1 出现的次数 一、数学思维解析 将1~ n的个位、十位、百位、...的1出现次数相加,即为1出现的总次数。 设数字n是个x位数,记n的第i位为ni,则可将n写为 nxnx−1⋯n2n1: 称" …...

如何成为程序员中的牛人/高手?
目录 一、牛人是怎么成为牛人的? 二、关于牛人的一点看法 三、让程序员与业务接壤,在开发团队中“升级” 四、使用低代码平台 目标效果 五、最后 祝伟大的程序员们梦想成真、码到成功! 一、牛人是怎么成为牛人的? 最近在某…...
云原生时代顶流消息中间件Apache Pulsar部署实操之轻量级计算框架
文章目录Pulsar Functions(轻量级计算框架)基础定义工作流程函数运行时处理保证和订阅类型窗口函数定义窗口类型滚动窗口滑动窗口函数配置函数示例有状态函数示例窗口函数示例自定义函数开发定义原生语言接口示例Pulsar函数SDK示例Pulsar Functions(轻量级计算框架) 基础定义 …...
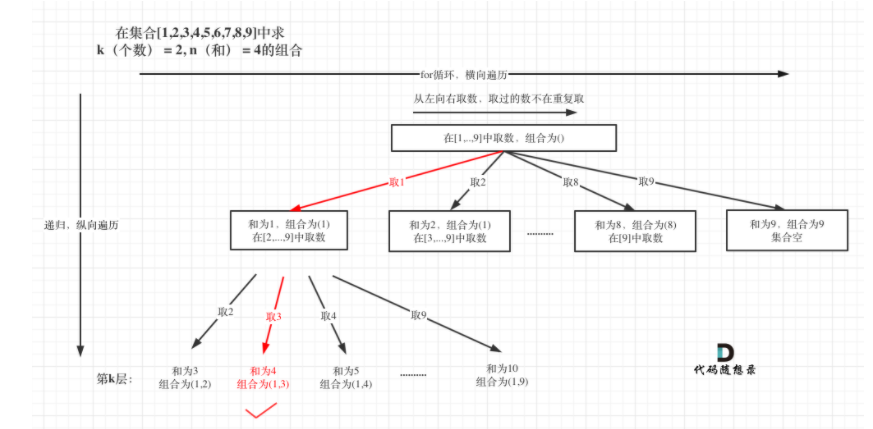
数据结构刷题(十九):77组合、216组合总和III
1.组合题目链接过程图:先从集合中取一个数,再依次从剩余数中取k-1个数。思路:回溯算法。使用回溯三部曲进行解题:递归函数的返回值以及参数:n,k,startIndex(记录每次循环集合从哪里开始遍历的位…...
PyQt 做美*女GIF设置桌面,每天都很爱~
人生苦短,我用python 要说程序员工作的最大压力不是来自于工作本身, 而是来自于需要不断学习才能更好地完成工作, 因为程序员工作中面对的编程语言是在不断更新的, 同时还要学习熟悉其他语言来提升竞争力… 好了,学习…...

[渗透测试笔记] 54.日薪2k的蓝队hw中级定级必备笔记系列篇3之域渗透黄金票据和白银票据
前文链接 [渗透测试笔记] 52.告别初级,日薪2k的蓝队hw中级定级必备笔记 [渗透测试笔记] 53.日薪2k的蓝队hw中级定级必备笔记2 文章目录 Kerberos认证协议NTLM认证协议Kerberos和NTLM比较黄金票据原理黄金票据条件复现过程白银票据原理白银票据条件复现过程黄金票据和白银票据…...

【异常】Spring Cloud Gateway网关自定义过滤器无法获取到请求体body的内容?不存在的!
一、需求说明 项目要使用到网关SpringCloud Gateway进行验签,现在定义了一个过滤器ValidateSignFilter, 我希望,所以过网关SpringCloud Gateway的请求,都能够校验一下请求头,看看是否有Sign这个字段放在请求头中。 二、异常说明 但是,我遇到了SpringCloud Gateway网关…...
)
CNN 卷积神经网络对染色血液细胞分类(blood-cells)
目录 1. 介绍 2. 加载数据 3. 可视化 3.1 显示单幅图像 3.2 显示多幅图像...
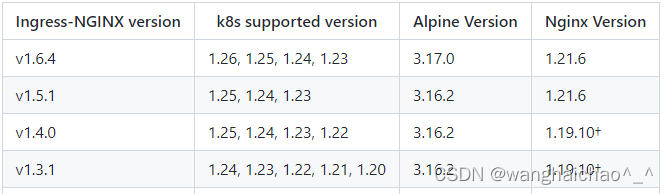
Kubernetes学习(三)Service
Service对象 为什么需要Service 每个Pod都有自己的IP地址,但是在Deployment中,在同一时刻运行的Pod集合可能与稍后运行该应用程序的Pod集合不同。 这就导致了一个问题:如果一组Pod(称为后端)为集群内其他Pod&#x…...
)
数学小课堂:古德-图灵折扣估计法和插值法(防范黑天鹅事件的方法)
文章目录 引言I 黑天鹅事件产生的原因1.1 置信度1.2 数据的稀疏性1.3 零概率问题II 防范黑天鹅事件的方法2.1 古德-图灵折扣估计法2.2 插值法引言 防范黑天鹅事件的方法 古德-图灵折扣估计法:它主要是解决零概率的事件古德的方法虽然解决了零概率的问题,但是依然没有解决数据…...

redis getshell方法
前言 参考文章 https://paper.seebug.org/1169 https://blog.csdn.net/weixin_55843787/article/details/123829606 https://blog.csdn.net/chenglanqi6606/article/details/100909518 Redis是什么 Redis是一款基于键值对的NoSQL数据库,它的值支持多种数据结构 …...
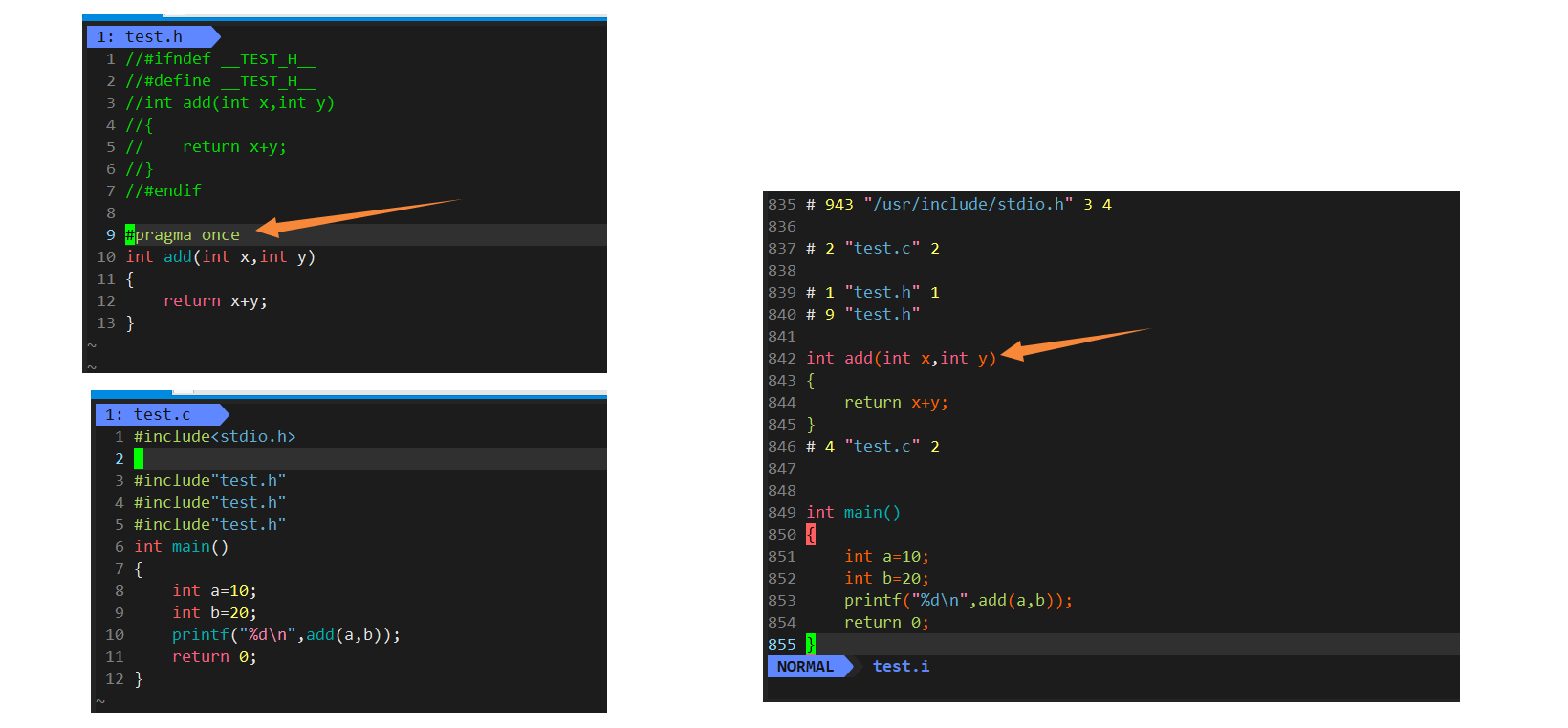
【ONE·C || 程序编译简述】
总言 C语言:程序编译相关。 文章目录总言1、程序的翻译环境和运行环境1.1、简述1.2、翻译环境:程序编译与链接1.2.1、简介:程序如何从.c文件形成.exe可执行程序1.2.2、过程说明1.3、运行环境2、预处理详解2.1、预定义符号2.2、#define2.…...

MGAT: Multimodal Graph Attention Network for Recommendation
模型总览如下: 图1:多模态图注意力网络背景:本论文是对MMGCN(Wei et al., 2019)的改进。MMGCN简单地在并行交互图上使用GNN,平等地对待从所有邻居传播的信息,无法自适应地捕获用户偏好。 MMGCN…...
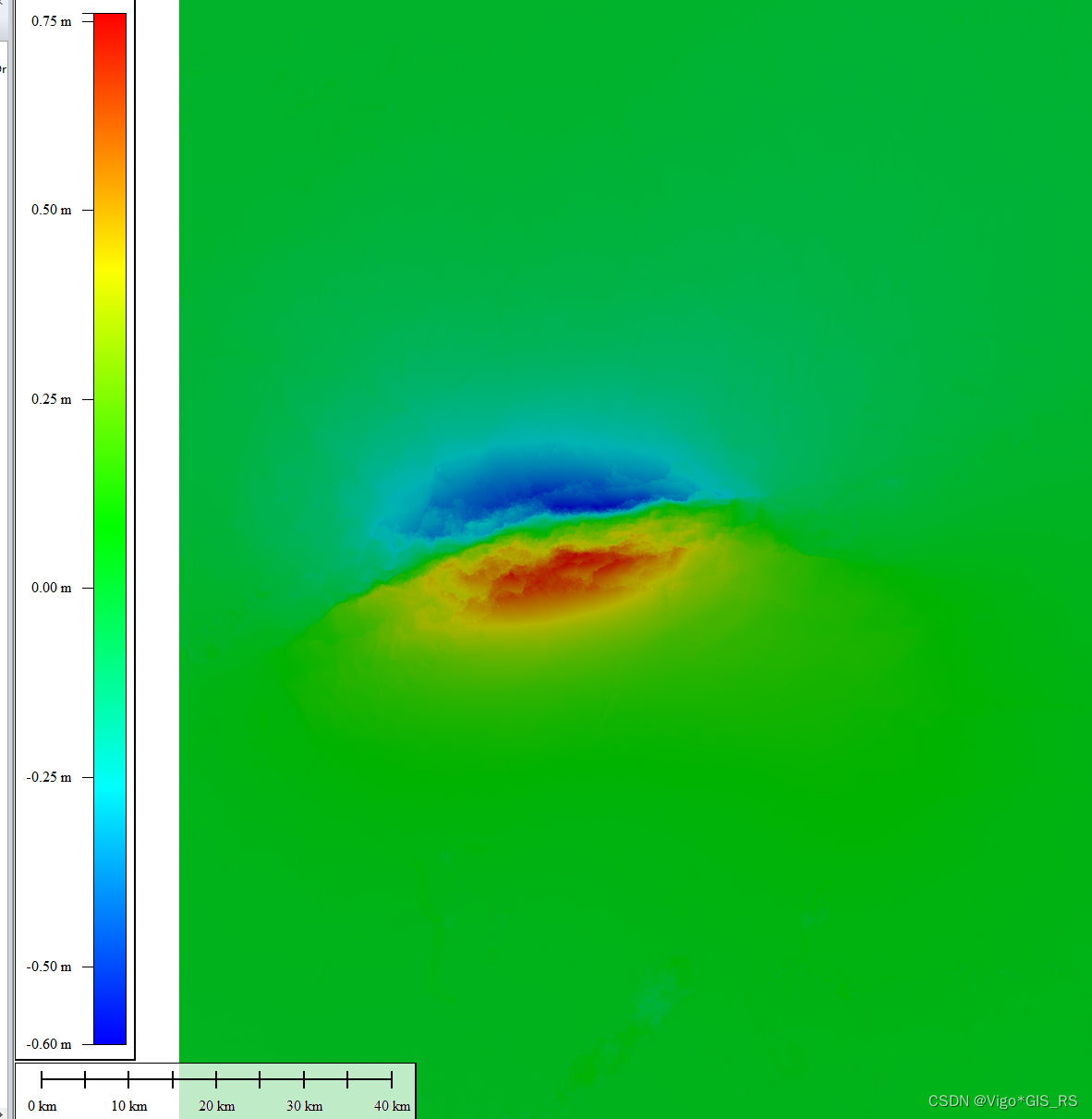
在SNAP中用sentinel-1数据做InSAR测量,以门源地震为例
在SNAP中用sentinel-1数据做InSAR0 写在前面1 数据下载2 处理步骤2.1 split2.2 apply orbit 导入精密轨道2.3 查看数据的时空基线base line2.4 back-geocoding 配准2.5 Enhanced Spectral Diversity2.6 Deburst2.7 Interogram Formation 生成干涉图2.8 Multilook 多视2.9 Golds…...
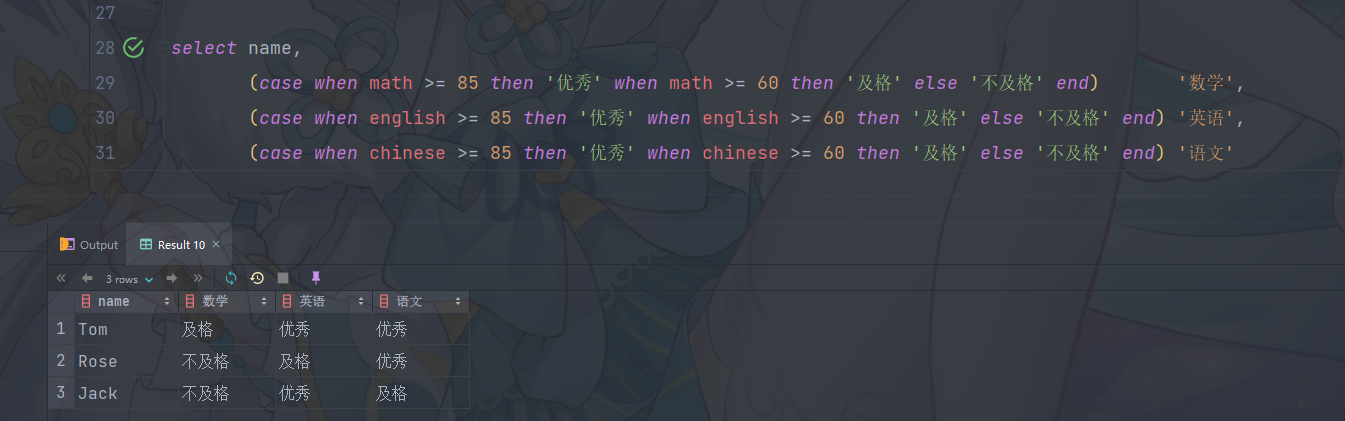
MySQL常用函数
什么是函数? 函数是指一段可以直接被另一段程序调用的程序或代码。 字符串函数 函数功能CONCAT(S1,S2,…Sn)字符串拼接,将S1,S2,… Sn拼接成一个字符串LOWER(str)将字符串str全部转为小写LOWER(str)将字符串str全部转为小写LPAD(…...

51单片机数字电子钟开题报告
目录 选题背景 初步设计方案 芯片的选型 编译环境 关键问题 策略 方案 参考文献 选题背景 数字电子钟是一种受到越来越多人喜爱的钟表,其准确性和稳定性成为设计和研发的重要考虑因素。在现代社会,时间的准确性对于各行各业都非常重要࿰…...

day7 HTTP协议
HTTP协议 什么是协议? 协议实际上是某些人,或者某些组织提前制定好的一套规范,大家都按照这个规范来,这样可以做到沟通无障碍。协议就是一套规范,就是一套标准。由其他人或其他组织来负责制定的。我说的话你能听懂&…...
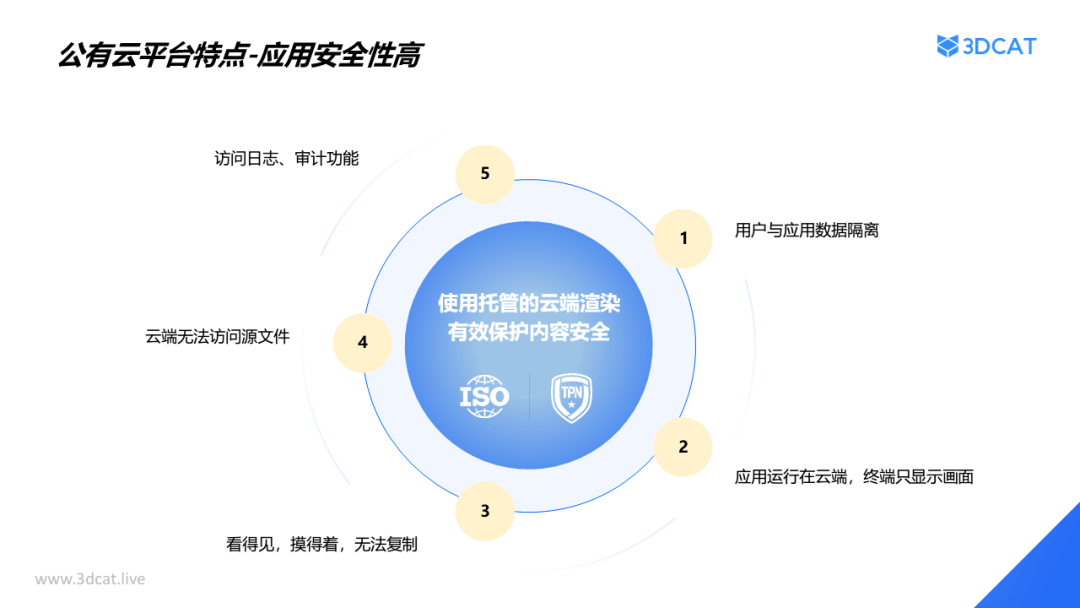
3DCAT+一汽奥迪:共建线上个性化订车实时云渲染方案
近年来,随着5G网络和云计算技术的不断发展,交互式3D实时云看车正在成为一种新的看车方式。与传统的到4S店实地考察不同,消费者可以足不出户,通过网络与终端设备即可实现全方位展示、自选汽车配色、模拟效果、快捷选车并进行个性化…...
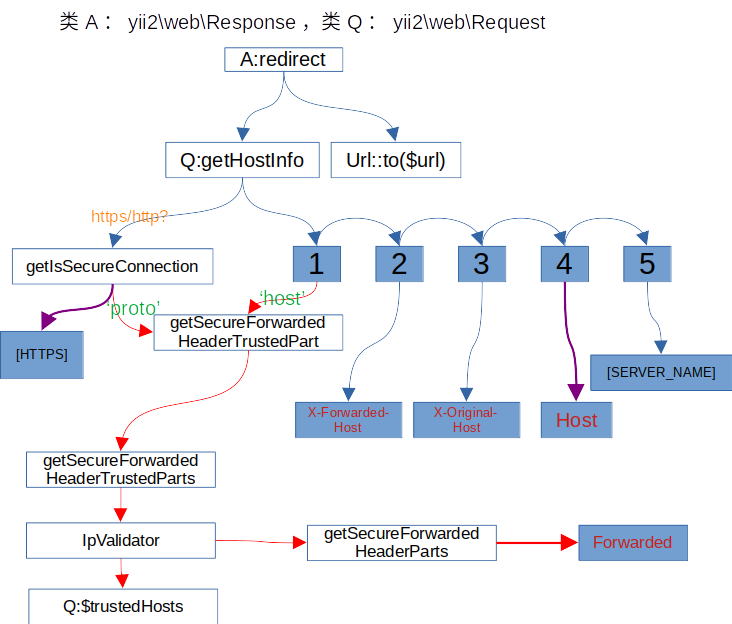
yii2项目使用frp https2http插件问题
yii2内网项目,使用frp进行内网穿透,使用 https2http插件把内网服务器http流量转成https,会存在一个问题:当使用 $this->redirect(...) 或 $this->goHome() (其实用的也是前者)等重定向时,…...

关于 interface{} 会有啥注意事项?下
我们一起来回顾一下上一次说到的 interface{} 可以用来做多态 接口类型分为空接口类型和非空接口类型,他们的底层数据结构不太一样 这里顺便说一下,用来作态需要满足这样的条件: 首先得有父类指针指向子类的对象这个接口还必须是非空接口…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
