C++:AVL树
AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下,时间复杂度为O(N);
两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。AVL树,即是高度平衡的二叉搜索树。
一棵AVL树是一棵平衡二叉搜索树,也能是一棵空树。
AVL树的性质:
①它的左右子树都是AVL树
②左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
③如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在log_2N,搜索的时间复杂度是log_2N。
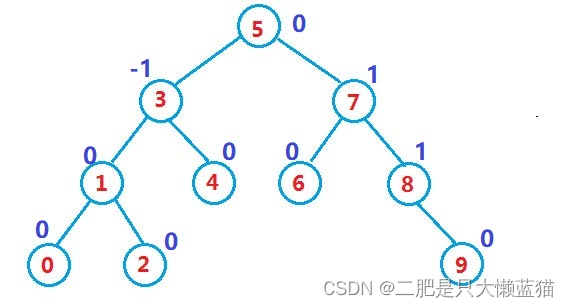
AVL树的定义:
AVL树的定义中:①拥有键值对。②多加一个双亲节点,用于调整平衡二叉树。③增加平衡因子,用于判断插入或删除后,是否还是一棵AVL树。
template<class K,class V>
struct AVLTreeNode
{pair<K, V> _kv;//键值对AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};
AVL树的插入
AVL树的插入分成两步:第一步是按照二叉搜索树的方式来新增节点。第二步是是调整节点,使其成为一棵平衡的二叉搜索树。
先展示代码,我们分析以下思路:
1.首先按照二叉搜索树的方式来新增节点,但这需要新增一个双亲指针,方便后续在调节节点。因此,在新增节点的最后部分的代码中,我们需要让cur->_parent指向双亲节点parent。
2.完成二叉搜索树的创建后,开始去判断各个节点的平衡因子。
①当平衡因子_bf等于0的时候,说明parent节点一边高一边矮,新增的这个节点填上了矮的地方,这种情况就不需要更新了,直接beak掉。
②当平衡因子_bf等于1或者-1的时候,说明parent原本的平衡因子是0,parent两边一样高,新增了节点之后,有一边变高了。这种情况需要继续往上走。
③当平衡因子_bf等于2或-2的时候,说明之前parent->_bf == 1 或者 -1,现在插入严重不平衡,违反规则,此时需要原地旋转,即以当前节点为轴旋转。
随后将重点分析:当平衡因子是2或-2的时候,说明需要通过旋转调节节点。那该如何去旋转呢?
bool Insert(const pair<K, V>& kv){//一开始是一棵空树if (_root == nullptr){_root = new Node(kv);return true;}//一开始不是空树Node* parent = nullptr;Node* cur = _root;//寻找插入的地方,是左子树还是右子树while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//找到插入的位置后,即确认了是在左子树还是右子树cur = new Node(kv);//确定是在父节点的左还是右if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子,判断插入后的树,是否是一棵AVL树while (parent){//插入的是在父节点的左边,即是左孩子if (cur == parent->_left){parent->_bf--;//一般是右-左,因此,如果是插入在左边,那就是减一}else //是右孩子{parent->_bf++;}//更新完平衡因子后,判断是否是一棵AVL树//如果平衡因子是0,任何节点的平衡因子都没被改变if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){//如果平衡因子是1或-1,那么就说明,父节点往上的节点的平衡因子有可能被改变了cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转//右单旋----高出来的那一部分按下去!if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if(parent->_bf==2 && cur->_bf== 1)//左单旋{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1) //先左旋后右旋{RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1) //先右旋再左旋{RotateRL(parent);}}else //不排除在创建一棵AVL树的时候,代码写错了{assert(false);}}return true;}旋转节点
旋转的要求:
⭐让这颗子树左右高度之差不超过1
⭐旋转过程中继续保持他是搜索树
⭐更新调整孩子节点的平衡因子
⭐让这颗子树的高度跟插入前保持一致。因为这样就不会对上层的平衡因子造成影响,此时就可以结束对这棵树的更新旋转。
旋转的情况有四种:
①新节点插入较高左子树的左侧---左左:右单旋
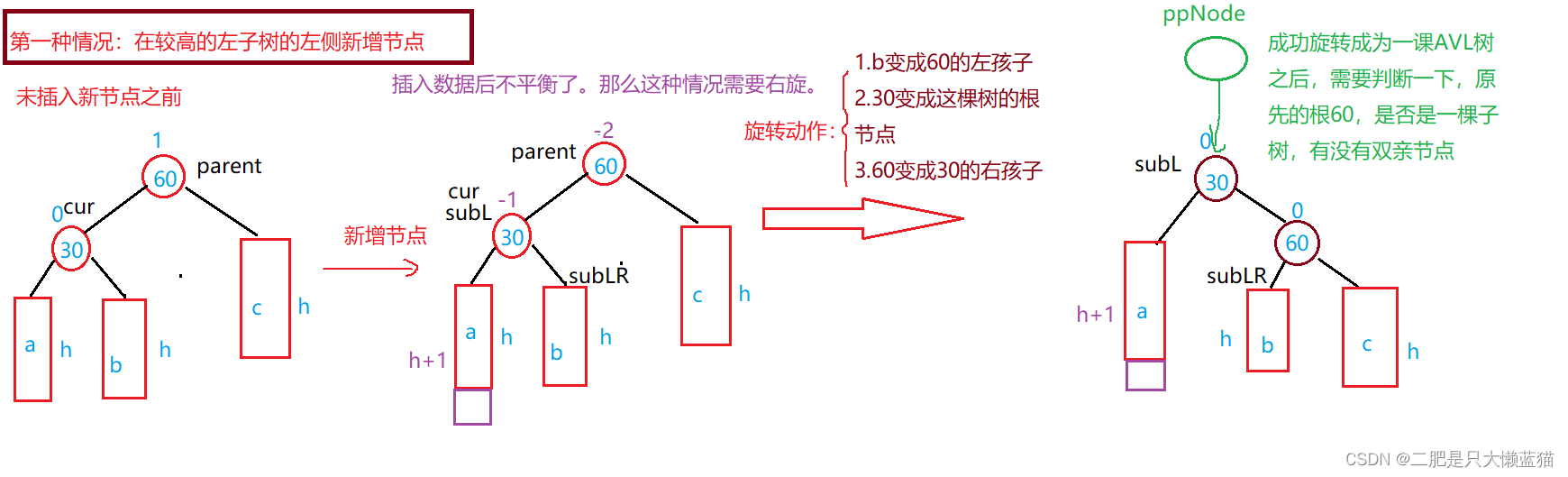
这种情况是新增的节点位于比较高的左子树的左侧的某个位置上,此时在往上检查平衡因子发现值为60的节点是平衡因子为-2,说明左子树的高度是比右子树高的(这里选择右减左),所以当我们的判断条件if(parent->_bf==-2 && cur->_bf == -1)成立时,就表示着符合当前情况。所以,我们需要将60的节点的平衡因子减小,那就是将它按下去!以60的节点为轴旋转:
⭐旋转的动作:因为b是30节点的右孩子,根据二叉搜索树的性质,b子树所有的值肯定是大于30,小于60的,而且60节点需要下来,说明60节点是要成为30节点的右孩子的,因此b子树就需要成为60节点的左孩子了。
⭐当然,我们需先判断一下,30节点的右孩子是否为空,即30节点没有右孩子。如果没有右孩子,那么就不能让它指向60节点的左孩子。
⭐然而,我们旋转的这颗树,可能是一颗子树,因此需要判断一下60节点的双亲节点是否为空,如果为空,说明它不是子树,此时就可以让_root指向subL,成为新的根,然后subL的双亲节点置为nullptr,因为subL->parent原本是指向60节点的。
⭐如果不为空,那就说明它是一棵子树,那么就让60节点的双亲节点的左或右孩子点指向30节点,30节点的双亲指向60原先的双亲节点。
右单旋的代码如下:
void RotateR(Node* parent){//一开始,例子中的60节点便是parent//先创建指向30节点的指针和指向b节点的指针Node* subL = parent->_left;Node* subLR = subL->_right;//这一步是让60节点的左孩子指向b节点parent->_left = subLR;//这一步判断b节点是否为空,如果不为空,那么就让它的双亲节点指向60节点(本来是指向subL的)if (subLR){subLR->_parent = parent;}//上面两步成功将b节点改链接到60节点上去//先保存60节点的双亲节点Node* ppNode = parent->_parent;//让30节点subL的右孩子指向60节点,即60节点链接到了30节点subL的右孩子上subL->_right = parent;//60节点的双亲节点指向30节点subLparent->_parent = subL;//判断60节点原本的双亲节点是否为空//为空if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else //不为空,说明是一棵子树{if (ppNode->_left == parent) //如果parent是原先的双亲节点的左孩子{ppNode->_left = subL; }else //如果parent是原先的双亲节点的右孩子{ppNode->_right = subL;}//链接后,再让成为新根后的30节点subL的双亲节点指向ppNodesubL->_parent = ppNode;}//最后将30节点subL和60节点parent的平衡因子修改//subL->_bf = parent->_bf = 0;//此时,右单旋完成//因为旋转的要求是让这颗子树的高度跟插入前保持一致//那就说明,此时完成旋转的这树,不会对上层的平衡因子造成影响,此时就可以结束对这棵树的更新旋转}②新节点插入较高右子树的右侧---右右:左单旋

这种情况是新增的节点位于比较高的右子树的右侧的某个位置上,此时在往上检查平衡因子发现值为30的节点是平衡因子为2,说明右子树的高度是比左子树高的(这里选择右减左),所以当我们的判断条件if(parent->_bf==2 && cur->_bf == 1)成立时,就表示着符合当前情况。所以,我们需要将30的节点的平衡因子减小,那就是将它按下去!以30的节点为轴旋转:
⭐旋转的动作:因为b是60节点的左孩子,根据二叉搜索树的性质,b子树所有的值肯定是大于30,小于60的,而且30节点需要下来,说明30节点是要成为60节点的左孩子孩子的,因此b子树就需要成为30节点的右孩子了。
⭐同样的,我们需先判断一下,60节点的左孩子是否为空,即60节点没有左孩子。如果没有左孩子,那么就不能让它指向30节点的右孩子。
⭐同样的,需要盘点一下是否是一棵子树。因此需要判断一下30节点的双亲节点是否为空,如果为空,说明它不是子树,此时就可以让_root指向subR,成为新的根,然后subR的双亲节点置为nullptr,因为subR->parent原本是指向30节点的。
⭐如果不为空,那就说明它是一棵子树,那么就让30节点的双亲节点的左或右孩子点指向60节点,60节点的双亲指向30原先的双亲节点。
左单旋代码如下:
void RotateL(Node* parent){//创建60节点subR,右右是左旋嘛Node* subR = parent->_right;//创建指向b节点的指针subRLNode* subRL = subR->_left;//先让parent的右孩子节点指向subRL。parent->_right = subRL;//判断subRL是否为空,不为空,那就让subRL的父节点指向parentif (subRL){subRL->_parent = parent;}//上面步骤成功将b节点链接到了parent上//先把parent的父节点保存起来,不管存在不存在Node* ppNode = parent->_parent;//接下来就是把parent按下了,成为subR的左孩子,让subR成为新根subR->_left = parent;parent->_parent = subR;//让subR成为新根if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left = parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}//修改平衡因子parent->_bf = subR->_bf = 0;}③新节点插入较高左子树的右侧---左右:先左单旋再右单旋
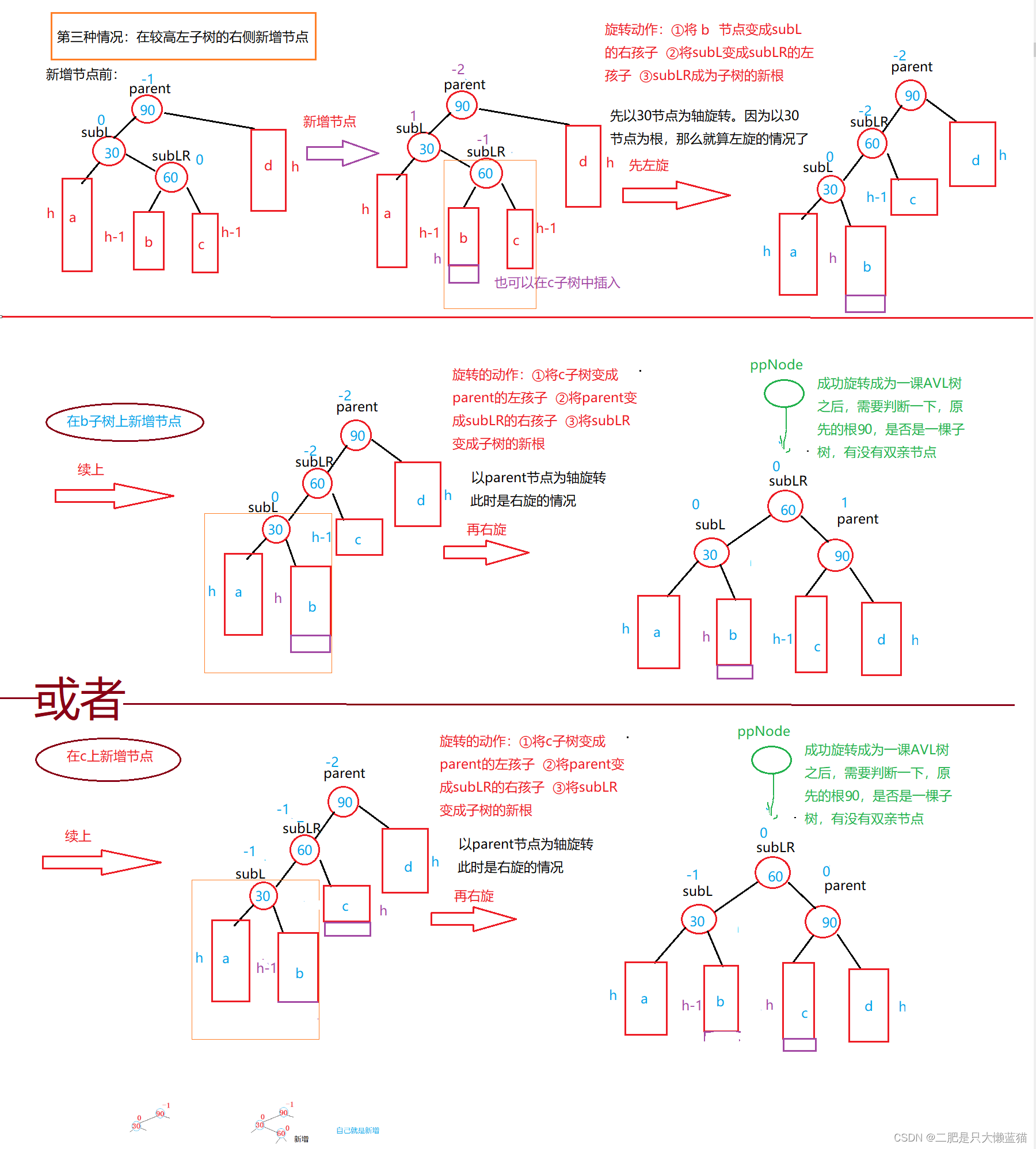
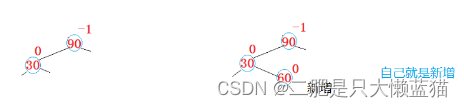
这种情况是新增的节点位于比较高的左子树的右侧的某个位置上,此时在往上检查平衡因子发现值为parent节点的平衡因子为-2,说明左子树的高度是比右子树高的(这里选择右减左),所以当我们的判断条件if(parent->_bf==-2 && cur->_bf == 1)成立时,就表示着符合当前情况。这种情况采取的旋转方式是先左旋后右旋。左旋的轴是subL节点,右旋的轴就是parent节点。
此时,我们复用左单旋和右单旋的情况即可。但是需要注意的是,尽管在右单旋和左单旋中,已经对平衡因子进行了修改,但我们通过画图可以看出来,修改过的平衡因子并不符合实际上的值,因此我们需要重新修改一遍。
代码如下:
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//记录调整节点之前,subLR的平衡因子,因为subLR最后是新根//开始调整RotateL(parent->_left);RotateR(parent);//修改平衡因子if (bf == -1)//说明是在左子树上新增节点,即图中的b子树{parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1)//说明是在右子树c上新增节点{parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if(bf==0)//说明subLR自己就是新增的节点{parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}④新节点插入较高右子树的左侧---右左:先右单旋再左单旋
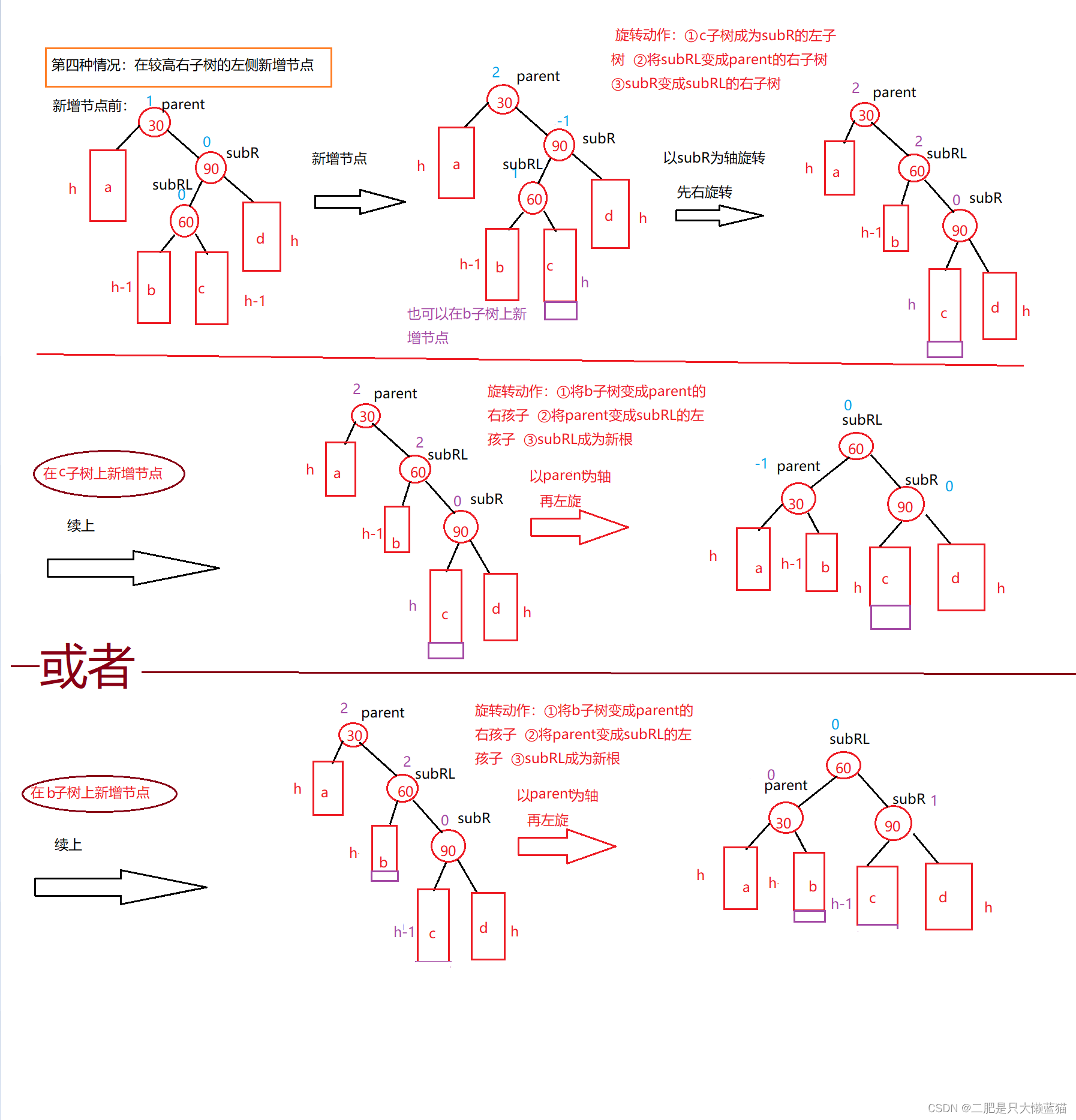
这种情况是新增的节点位于比较高的右子树的左侧的某个位置上,此时在往上检查平衡因子发现值为parent节点的平衡因子为2,说明右子树的高度是比左子树高的(这里选择右减左),所以当我们的判断条件if(parent->_bf==2 && cur->_bf == -1)成立时,就表示着符合当前情况。这种情况采取的旋转方式是先右旋后左旋。右旋的轴是subR节点,左旋的轴就是parent节点。
此时,我们复用左单旋和右单旋的情况即可。但是需要注意的是,尽管在右单旋和左单旋中,已经对平衡因子进行了修改,但我们通过画图可以看出来,修改过的平衡因子并不符合实际上的值,因此我们需要重新修改一遍。
代码如下:
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//记录调整节点之前,subRL的平衡因子,因为subRL最后是新根RotateR(parent->_right);RotateL(parent);if (bf == 1) //在右子树上新增节点{parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1) //在左子树上新增节点{parent->_bf = 0;subR->_bf = -1;subRL->_bf = 0;}else if (bf == 0) //说明subRL本身就是那个新增的节点{parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}总结:
假如以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑:
①pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR。
当pSubR的平衡因子为1时,执行左单旋
当pSubR的平衡因子为-1时,执行右左双旋
②pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL
当pSubL的平衡因子为-1是,执行右单旋
当pSubL的平衡因子为1时,执行左右双旋
旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
验证AVL树
由于AVL树是在二叉搜索树的基础上加了平衡性后得到的树,因此需要确认一棵树是AVL树,那么就需要以下两步:
1.先确定是否是一棵二叉搜索树:如果中序遍历可得到一个有序的序列,就说明为二叉搜索树。
2.验证其是否平衡:①每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)。②节点的平衡因子是否计算正确。
代码如下:
①中序遍历:
void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ": " << root->_kv.second << endl;_Inorder(root->_right);}②计算高度:
int Height(Node* root){if (root == nullptr){return 0;}//先计算左子树的高度int ln = Height(root->_left);//然后计算右子树的高度int rn = Height(root->_right);return ln > rn ? ln + 1 : rn + 1;}③验证平衡:
bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(Node* root){if (root == nullptr)return true;//计算当前节点root的平衡因子int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);//如果不同,那就将当前节点的值打印出来,并提升异常if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}//通过递归,验证每一个节点的平衡因子是否符合return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);}AVL树性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即log_2 (N)。
但是如果要对AVL树做一些结构修改的操作,性能非常低下,因为做修改就很大可能需要进行旋转,每一次旋转都是比较消耗性能的!
相关文章:

C++:AVL树
AVL树的概念 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下,时间复杂度为O(N); 两位俄罗斯的数学家G.M.Ade…...
Docker中安装Oracle-12c
前言 MySQL和Oracle是开发中常用到的两个关系型数据库管理系统,接上一期内容,这一期在Docker中完成oracle-12c的安装和配置。 安装oracle-12c 1、拉取oracle-12c镜像 启动Docker Desktop后在cmd窗口中执行docker search oracle命令,搜索O…...

教你如何用Python分析出选注双色球号码
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 又到了学Python时刻~ 数据集介绍 找从19年到现在的开奖历史数据,我们首先要把这个历史数据拿到, 拿到我们再进行做分析,分析每个号码出现的频率是多少, 哪个多&#x…...

elasticsearch映射及字段类型
查询映射关系类型上对字段的类型进行映射,我们前面知道可以通过get方法请求_mapping查询指定类型的映射关系:此语句可以查询get-together索引下的group类型的映射关系更新映射关系使用put方法可以更新类型的映射这里指定了new-events类型的字段映射关系&…...
)
1493围圈报数(队列)
题目描述 有n个人依次围成一圈,从第1个人开始报数,数到第m个人出列,然后从出列的下一个人开始报数,数到第m个人又出列,…,如此反复到所有的人全部出列为止。…...
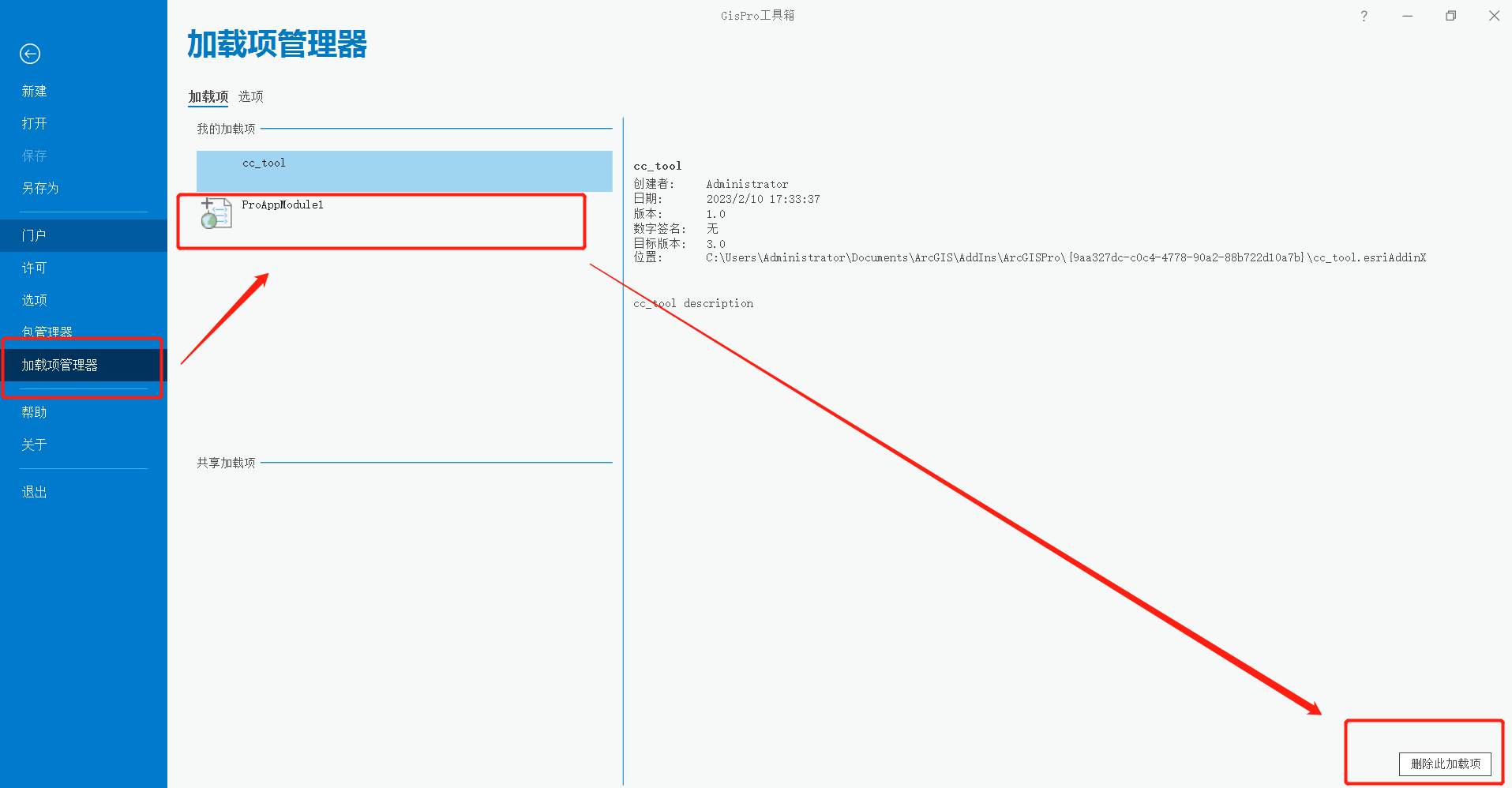
【ArcGIS Pro二次开发】(2):创建一个Add-in项目
Add-In即模块加载项,是一种能够快速扩展桌面应用程序功能的全新扩展方式。 一、创建新项目 1、打开VS2002,选择创建新项目。 2、在搜索框中输入“arcgis pro”,在搜索结果中选择【ArcGIS Pro 模块加载项】创建项目,注意选择语言应…...
浏览器缓存是如何提升网站访问速度的
提升速度,降低负载 浏览器访问一个页面时,会请求加载HTML、CSS和JS等静态资源,并把这些内容渲染到屏幕上。 对浏览器来说,如果页面没有更新,每次都去请求服务器是没有必要的。所以,把下载的资源缓存起来&…...

Linux中几个在终端中有趣的命令
uhh…最近我不知道该更新些什么,所以就更新Linux几个很有趣的命令 文章目录前言1.命令:sl安装 sl输出2. 命令:telnet命令:fortune安装fortune4.命令:rev(反转)安装rev5. 命令:factor…...

快来来试试SpringBoot3 中的新玩意~
你还在用OpenFeign嘛?快来试试 SpringBoot3 中的这个新玩意!声明式HTTP调用 1、由来 Spring Boot3 去年底就已经正式发布,我也尝了一把鲜,最近有空会和小伙伴们慢慢聊聊 Spring Boot3 都给我们带来了哪些新东西。 今天我们就先…...

【寻人启事】达坦科技持续招人ing
❤️一起来探索前沿科技,做有意思的事情~ 我们是谁 达坦科技(DatenLord)专注于打造新一代开源跨云存储平台。通过软硬件深度融合的方式打通云云壁垒,实现无限制跨云存储、跨云联通,建立海量异地、异构…...

【C/C++基础练习题】简单函数练习题
🍉内容专栏:【C/C要打好基础啊】 🍉本文内容:简单函数使用练习题(复习之前写过的实验报告) 🍉本文作者:Melon西西 🍉发布时间 :2023.2.11 目录 1.给定某个年…...

【代码随想录训练营】【Day11】第五章|栈与队列|20. 有效的括号|1047. 删除字符串中的所有相邻重复项|150. 逆波兰表达式求值
20. 有效的括号 题目详细:LeetCode.20 由题可知,有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一个对应的相同类型的左括号。 那么,我们可以利用栈后进先出的特点&#x…...

基于云原生分布式存储ceph实现k8s数据持久化
文章目录1、初始化集群1.1 集群机器配置1.2 配置主机名1.3 配置hosts文件1.4、配置互信1.5、关闭防火墙1.6、关闭selinux1.7、配置Ceph安装源1.8、配置时间同步1.9、安装基础软件包2、安装ceph集群2.1 安装ceph-deploy2.2 创建monitor节点2.3 安装ceph-monitor2.4 部署osd服务2…...

SpringMVC获取请求参数
SpringMVC获取请求参数 通过ServletAPI获取 将HttpServletRequest作为控制器方法的形参,此时HttpServletRequest类型的参数表示封装了当前请求的报文对象。 RequestMapping("/testServletAPI") // request表示当前请求 public String testServletAPI(H…...

详解浏览器从输入URL到页面展示的过程
用户发出 URL 请求到页面开始解析的这个过程,就叫做导航。 1. 用户输入 当用户在地址栏中输入一个查询关键字时,地址栏会判断输入的关键字是搜索内容,还是请求的 URL。 当用户输入关键字并键入回车之后,这意味着当前页面即将要…...

【吉先生的Java全栈之路】
吉士先生Java全栈学习路线🧡第一阶段Java基础: 在第一阶段:我们要认真听讲,因为基础很重要!基础很重要!基础很重要!!! 重要的事情说三遍。在这里我们先学JavaSE路线;学完之后我们要去学第一个可视化组件编程《GUI》;然后写个《贪吃蛇》游戏耍…...

第二章 Opencv图像处理基本操作
目录1.读取图像1-1.imread()方法2.显示图像2-1.imshow()方法2-2.waitKey()方法2-3.destroyAllWindows()方法2-4.小总结3.保存图像3-1.imwrite()方法4.查看图像属性4-1.常见的三个图像属性1.读取图像 要对一幅图像进行处理,第一件事就是要读取这幅图像。 1-1.imread(…...
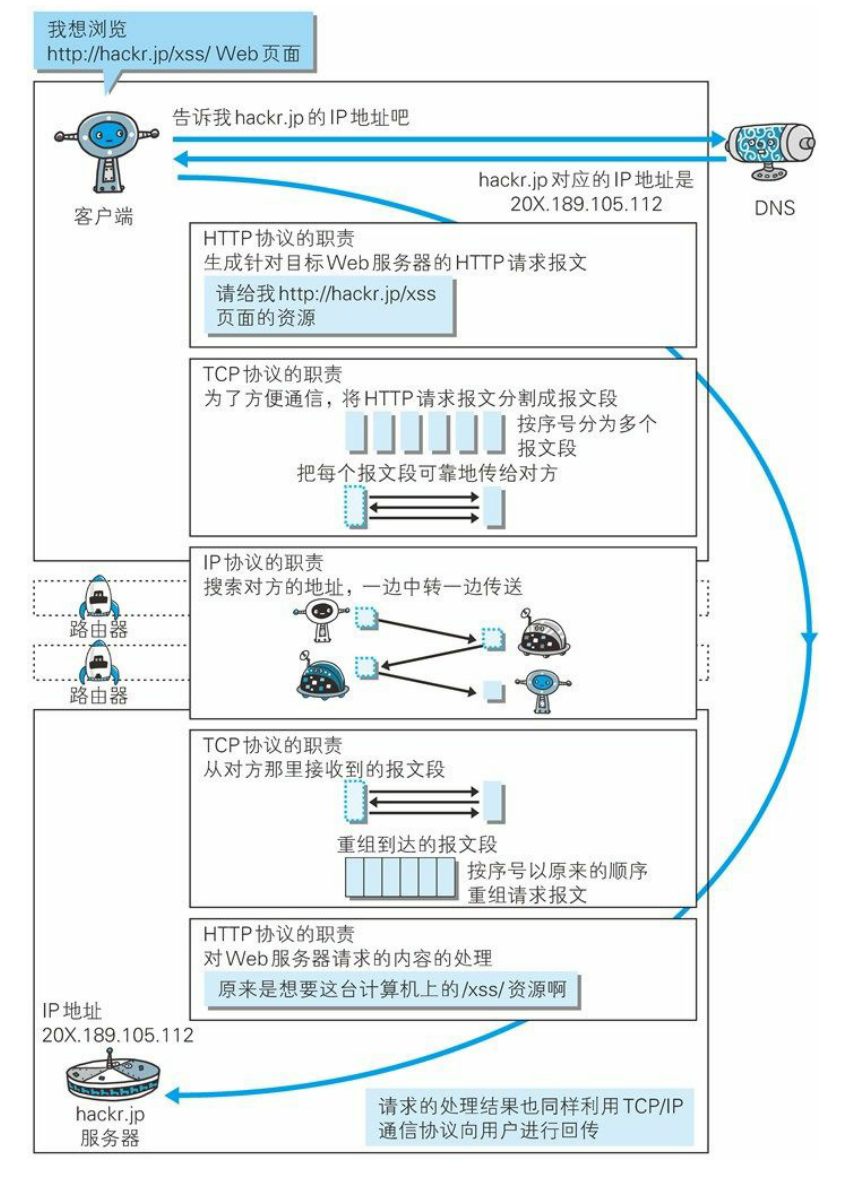
字节一面:在浏览器地址栏输入一个 URL 后回车,背后发生了什么?
近段时间,有小伙伴面试字节,说遇到一个面试题: 在浏览器地址栏输入一个 URL 后回车,背后发生了什么? 这里尼恩给大家做一下系统化、体系化的梳理,使得大家可以充分展示一下大家雄厚的 “技术肌肉”…...
推荐3dMax三维设计十大插件
3dMax是一款功能非常强大的三维设计软件,但无论它的功能多么强大,也不可能包含所有三维方面的功能,这时候,第三方插件可以很好的弥补和增强3dMax的基本功能,下面就给大家介绍十款非常不错的3dMax插件。 森林包…...
Arduino IDE 2.0.6中 ESP32开发环境搭建笔记
Arduino IDE 2.0.6中 ESP32开发环境搭建 Arduino IDE2.0 已上线一段时间,以后ESP32的学习转至新的IDE中 ,需对开发环境进行。 Arduino IDE2.0与1.0有很大差异。原来环境搭建方法已完全不同。下文主要记录环…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
