包子凑数【蓝桥杯】/完全背包
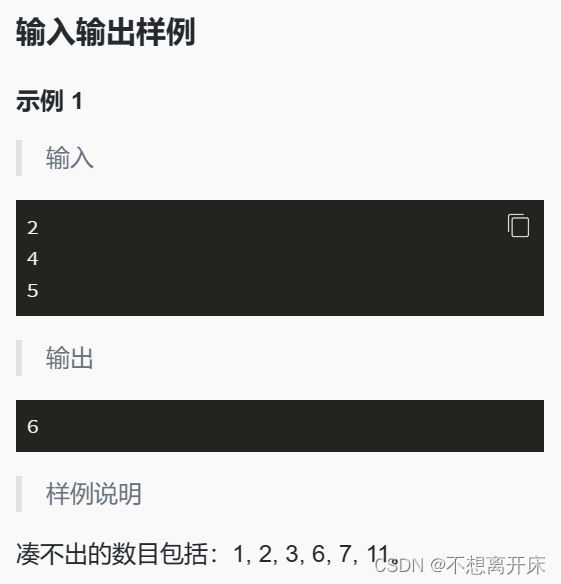
包子凑数



完全背包
完全背包问题和01背包的区别就是,完全背包问题每一个物品能取无限次。
思路:当n个数的最大公约数不为1,即不互质时,有无限多个凑不出来的,即n个数都可以表示成kn,k为常数且不为1。当n个数的最大公约数为1,到了某个数之后就全都可以凑出来。
根据本题的数据,可以直接遍历到10010就行
#include<iostream>
using namespace std;
//dp[i]表示i这个数可不可以被凑出来
int dp[10010];
//欧几里得算法求最大公约数
int gcd(int a,int b)
{return (b==0)?a:gcd(b,a%b);
}
int main()
{int n;cin>>n;int a[n],g;for(int i=0;i<n;i++) {cin>>a[i];if(i==0) g=a[i];else g=gcd(g,a[i]);}if(g!=1){cout<<"INF"<<endl;return 0;}dp[0]=1;//完全背包for(int i=0;i<n;i++){for(int j=a[i];j<10010;j++){dp[j]=max(dp[j],dp[j-a[i]]);}}int ans=0;for(int i=0;i<10010;i++){if(!dp[i]) ans++;}cout<<ans<<endl;return 0;
}
相关文章:

包子凑数【蓝桥杯】/完全背包
包子凑数 完全背包 完全背包问题和01背包的区别就是,完全背包问题每一个物品能取无限次。 思路:当n个数的最大公约数不为1,即不互质时,有无限多个凑不出来的,即n个数都可以表示成kn,k为常数且不为1。当n个…...

口语 4.6
drop the gun :逃避 radically 极大程度地 vastly cognition:认知能力 flaw缺陷 flawless:没有缺陷 interface:接口,交流处 retain:保留 down the rabbit hole:进入未知领域了 wrap your head aro…...

使用Docker 部署jenkins 实现自动化部署
使用Docker部署jenkins实现自动化部署ruoyi-vue docker jenkinsJava jenkinsfilevue jenkinsfileDockerfile 部署脚本Java Dockerfilenginx Dockerfilenginx-dev.conf 使用docker部署Jenkins,项目: https://gitee.com/y_project/RuoYi-Vue 作为部署项目示范 docker…...
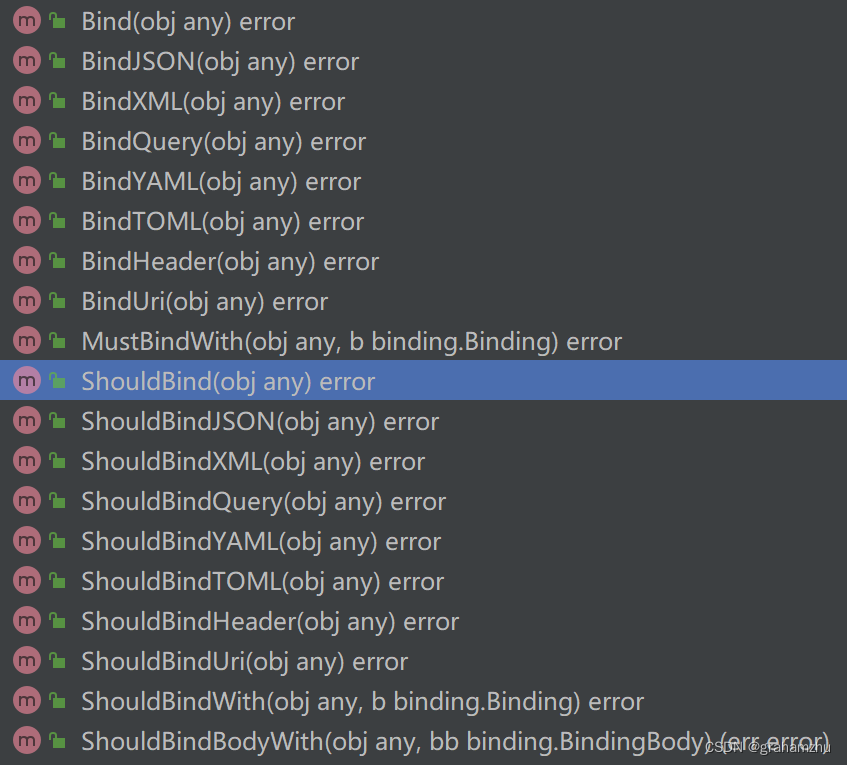
golang语言系列:Web框架+路由 之 Gin
云原生学习路线导航页(持续更新中) 本文是golang语言学习系列,本篇对Gin框架的基本使用方法进行学习 1.Gin框架是什么 Gin 是一个 Go (Golang) 编写的轻量级 http web 框架,运行速度非常快,如果你是性能和高效的追求者…...

春招百题--堆
一、堆的定义 二、堆(优先队列) 堆通常用于实现优先队列(priority_queue),大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构。 堆的…...

全志A40i android7.1 移植wifi驱动的一般流程
一,问题分析 一般情况下移植一款模组,会涉及到驱动,firmware, hal层,方案端的适配。 下面以RTL8723ds为例详细列出移植的通用步骤。 二,移植步骤 1. 移植Wi-Fi驱动 从RTL原厂或者已经支持的其他把内核版本中获取驱动…...
)
Qt——Qt绘图之QPainter的使用总结(使用paintEvent实现旋转图片效果)
【系列专栏】:博主结合工作实践输出的,解决实际问题的专栏,朋友们看过来! 《项目案例分享》 《极客DIY开源分享》 《嵌入式通用开发实战》 《C++语言开发基础总结》 《从0到1学习嵌入式Linux开发》 《QT开发实战》 《Android开发实战》...

Day83:服务攻防-开发组件安全JacksonFastJson各版本XStreamCVE环境复现
目录 J2EE-组件Jackson-本地demo&CVE 代码执行 (CVE-2020-8840) 代码执行 (CVE-2020-35728) J2EE-组件FastJson-本地demo&CVE FastJson < 1.2.24 FastJson < 1.2.47 FastJson < 1.2.80 (利用条件比较苛刻) J2EE-组件XStream-靶场&CVE …...

【QT+QGIS跨平台编译】056:【pdal_kazhdan+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
点击查看专栏目录 文章目录 一、pdal_kazhdan介绍二、pdal下载三、文件分析四、pro文件五、编译实践一、pdal_kazhdan介绍 pdal_kazhdan 是 PDAL(Point Data Abstraction Library)相关的 Kazhdan 算法的实现。PDAL 是一个用于处理和分析点云数据的开源库,而 Kazhdan 算法通常…...

泰坦尼克号幸存者数据分析
泰坦尼克号幸存者数据分析 1、泰坦尼克号数据集2、数据集加载与概览3、泰坦尼克号幸存者数据分析4、哪些人可能成为幸存者? 1、泰坦尼克号数据集 泰坦尼克号的沉没是世界上最严重的海难事故之一,造成了大量的人员伤亡。这是一艘号称当时世界上最大的邮轮…...
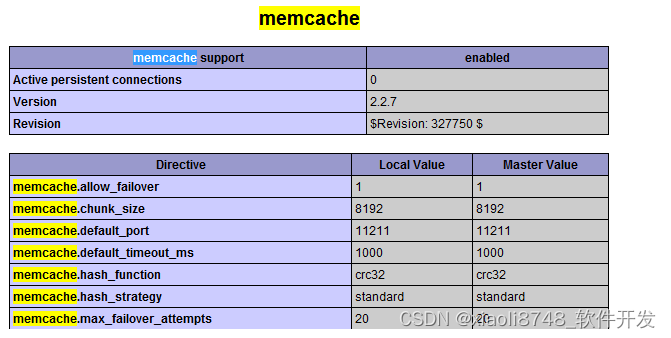
Memcached 教程之 PHP 连接 Memcached 服务(十)
PHP 连接 Memcached 服务 在前面章节中我们已经介绍了如何安装 Memcached 服务,接下来我们为大家介绍 PHP 如何使用 Memcached 服务。 PHP Memcache 扩展安装 PHP Memcache 扩展包下载地址:PECL :: Package :: memcache,你可以下载最新稳定…...
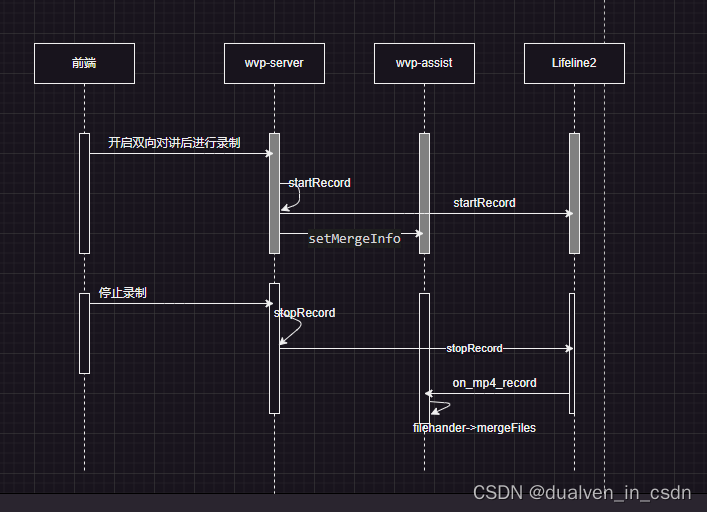
【zlm】音视频流与音频流合并的设计
目录 设想一 设想二 方案三 关键技术 测试语句 测试脚本 参考文档 设想一 //开始录制_option.mp4_save_path custom_path;_option.mp4_max_second max_second;vector<Track::Ptr> mytracks getTracks();auto src MediaSource::find( DEFAULT_VHOST, "1&quo…...

typescript的工作流
先coding code.ts代码,由tsc编译code.ts生成code.js格式 npm install —save-dev lite-server 是用来安装轻量级的服务器,只是用来开发的一个服务器,真正到生产环境中时可能会使用类似于Apache的server或者汤姆猫一类的服务器,安…...

MATLAB下载与安装详细教程:从官方获取到成功启动
引言 MATLAB(MATrix LABoratory)作为一款全球知名的高级数值计算与数据分析平台,以其强大的矩阵运算能力、丰富的内置函数库以及直观易用的图形用户界面,深受科研人员、工程师和学生群体的青睐。无论是进行复杂的数学建模、信号处…...

【随笔】Git 高级篇 -- 分离 HEAD(十一)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...
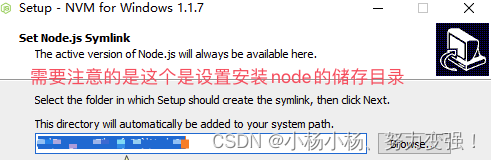
mac、windows 电脑安装使用多个版本的node
我们为啥要安装多个不同版本的node? 开发旧项目时,使用低版本Nodejs。开发新项目时,需使用高版本Node.js。可使用n同时安装多个版本Node.js,并切换到指定版本Node.js。 mac电脑安装 一、全局安装 npm install -g n 二、mac电脑…...
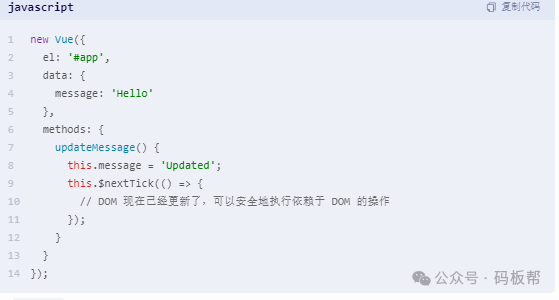
vue 浅解watch cli computed props ref vue slot axios nexttick devtools说明使用
Vue.js 是一个强大的前端框架,它提供了很多有用的功能和工具。你提到的这些特性(watch、cli、computed、props、ref、slot、axios、nextTick、devtools)在 Vue 中各自扮演着不同的角色。下面我会逐一解释这些特性如何在 Vue 中使用࿱…...
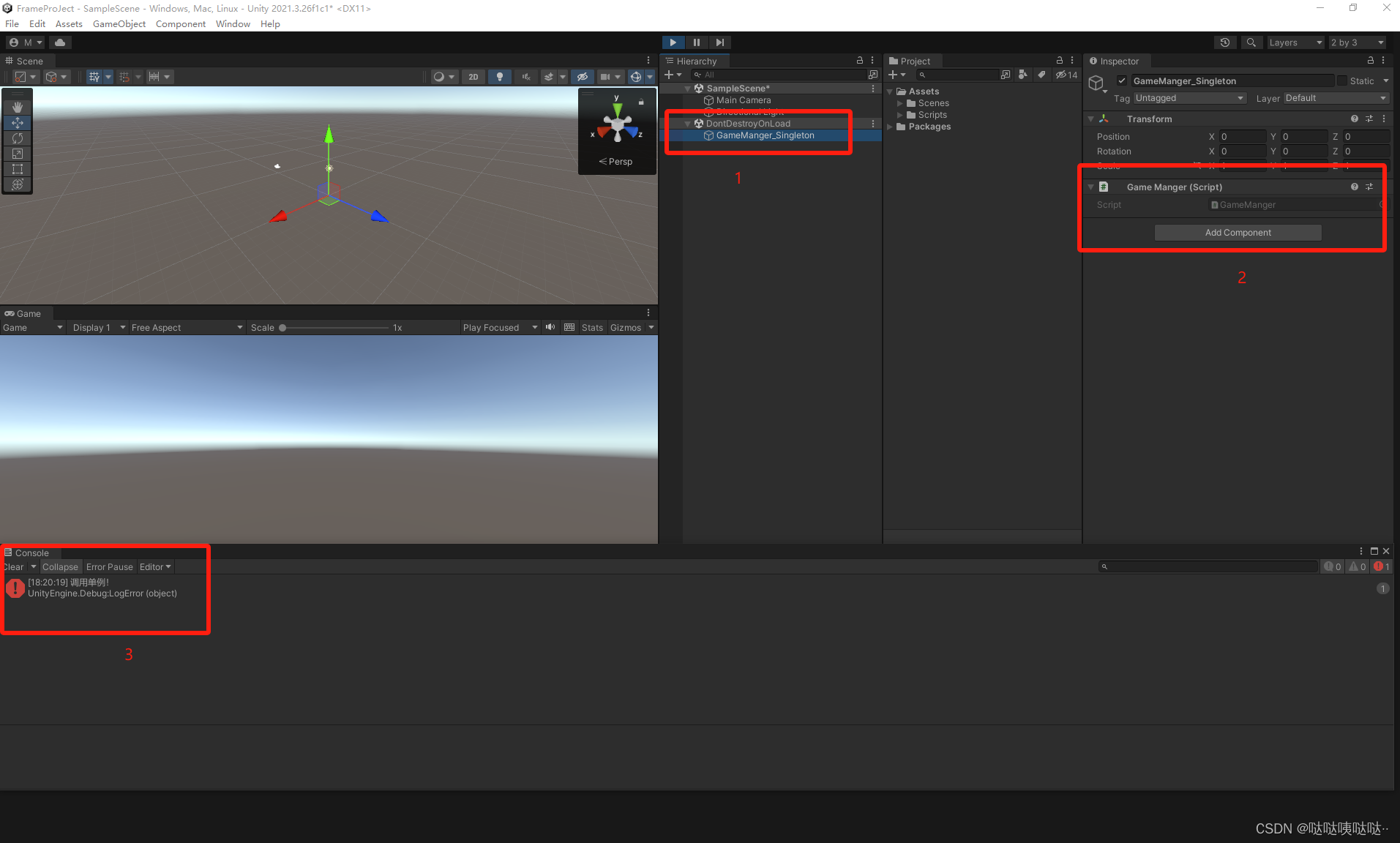
Unity自定义框架(1)-----------单例模式
前言: Unity作为一款强大的游戏开发引擎,其基础框架的设计对于项目的结构和性能有着重要的影响。其中,单例模式是一种常用的设计模式,用于确保一个类只有一个实例,并提供一个全局访问点。 什么是单例模式?…...
04-自媒体文章-自动审核
自媒体文章-自动审核 1)自媒体文章自动审核流程 1 自媒体端发布文章后,开始审核文章 2 审核的主要是审核文章的内容(文本内容和图片) 3 借助第三方提供的接口审核文本 4 借助第三方提供的接口审核图片,由于图片存储到minIO中&…...

LeetCode-热题100:763. 划分字母区间
题目描述 给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。 返回一个表示每个字符串片段的长度的列表。…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
