逻辑优化基础-bi-decomposition
简介
bi-decomposition是逻辑综合中用于简化布尔函数的一种技术。其思想是将函数分成两个较小的函数,每个函数仅取决于所选变量的一个值。这些较小的函数可以使用简单的逻辑门(如AND、OR和NOT门)来实现,然后组合以获得原始函数的输出。这可能会导致原始布尔函数的更简单和更有效的实现。
bi-decomposition的过程涉及选择一个变量进行分割,根据该变量的值创建两个函数,然后使用以下恒等式将原始函数表示为这些较小函数的组合:
F = F1B + F0B'
其中F是原始函数,F1是选定变量为1时的函数,F0是选定变量为0时的函数,B是选定的变量。这个恒等式是代数的分配律的布尔版本,它允许我们将原始函数F表示为两个较小函数的和,每个函数仅取决于所选变量的一个值。
一旦我们使用较小函数表达了原始函数,我们就可以使用简单的逻辑门来实现这些较小函数,然后将它们组合以获得原始函数的输出。这可能会导致原始布尔函数的更简单和更有效的实现,因为较小的函数可能使用更少的逻辑门更容易实现。
bi-decomposition是逻辑综合中简化和优化布尔函数的一种强大技术。当原始函数复杂且难以使用直接方法实现时,一般可以尝试使用bi-decomposition。
示例
假设考虑这样一个布尔函数:
F(A, B, C, D) = A'B + AB'C + BCD
应用bi-decomposition到该函数的第一步是选择一个变量进行分割。让我们选择变量B进行分割,这意味着我们基于B的值创建两个函数:一个函数其中B为1(我们称其为F1),另一个函数其中B为0(我们称其为F0)。这些函数可以写成:
F1(B=1) = A'C + CD
F0(B=0) = A'
接下来,我们需要找到一种用F1和F0的方式来表达原始函数F的方法。我们可以使用以下恒等式:
F = F1B + F0B'
在这种情况下,我们可以写成:
F = (A'C + CD)B + A'B'
这就是相对于变量B的F的 bi-decomposition。同理我们也可以得到基于变量 C的 bi-decomposition 表达式:
F(A, B, C, D) = A'B + AB'C + BCDF1(C=1) = A'B + AB' + BD
F0(C=0) = A'BF = F1C + F0C' = (A'B + AB' + BD)C + A'BC'
实际上,如果我们再调用一个rewrite算法,还可以变换为以下形式:
F = F1C + F0C' = (A^B + BD)C + A'BC'
以上是对于 bi-decomposition的基础介绍,欢迎指正错误。
相关文章:

逻辑优化基础-bi-decomposition
简介 bi-decomposition是逻辑综合中用于简化布尔函数的一种技术。其思想是将函数分成两个较小的函数,每个函数仅取决于所选变量的一个值。这些较小的函数可以使用简单的逻辑门(如AND、OR和NOT门)来实现,然后组合以获得原始函数的…...

Modbus转profinet网关连接1200PLC在博图组态与驱动器通讯程序案例
本案例给大家介绍由兴达易控modbus转profinet网关连接1200PLC在博图软件无需编程,实现1200Profinet转modbus与驱动器通讯的程序案例 硬件连接:1200PLC一台;英威腾DA180系列驱动器一台;兴达易控modbus转profinet网关一台 下面就是…...

Android ART虚拟机 启动和初始化
前言 之前整理了一系列Dalvik虚拟机的关于堆内存和GC的文章,轮到对ART内存进行分析优化了,继续整理输出一波,本篇为ART虚拟机系列的第一篇,介绍ART虚拟机的启动和初始化。 #mermaid-svg-8iNdLFTpOHLgRjHA {font-family:"tre…...

宇视科技一二三面
一面 1、自我介绍 2、堆和栈的区别,堆在数据结构中是如何表示的 3、有用过Linux吗?虚拟空间中用户态是3G,假如计算机的内存是4G,为什么计算机可以运行这些进程 4、虚拟地址到物理地址的映射过程 5、进程间的通信方式 6、共享内存…...
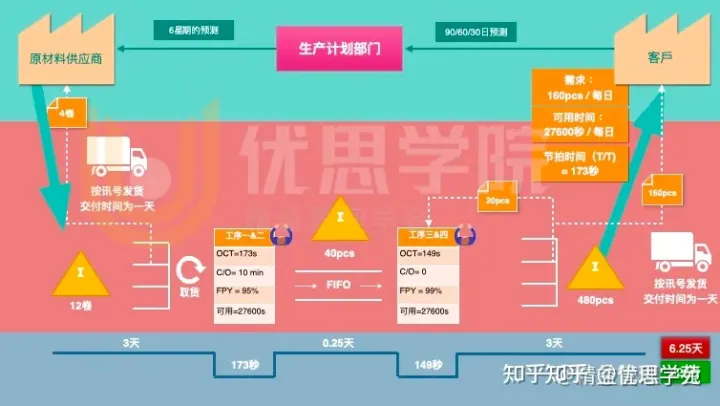
优思学院|盘点,精益生产25个工具!【必需收藏】
精益生产方法需要一种全面的方法才能有效实施。精益这个概念是每个接触产品供应链的人都要实践的,无论是在计划方面还是在分析方面。 精益生产工具有助于持续改进生产效率和产品或服务质量。精益工具是要减少 Muda (浪费),从生产过…...

Linux中将多块新硬盘合并成一个,挂载到/mysqldata目录下
需求: 将两块空硬盘合并为“一块”,挂载到指定目录(/data)下,达到在一个目录使用2块硬盘所有空间的效果。 使用 fdisk -l 命令查看当前系统中的硬盘,如下图: 系统中存在两块未分配的硬盘&#…...

Git的SSH密钥配置
Git的SSH密钥配置简记Githttps和ssh的区别基本需求SSH密钥类型ED25519 SSH 密钥RSA SSH 密钥查看您是否有现有的 SSH 密钥对设置流程设置user name和emailssh密钥配置检查是否存在ssh Key创建新的ssh key将ssh密钥添加到您的Git帐户验证您是否可以连接使用Git有一段时间了&…...

C++回顾(九)——多继承
9.1 多继承 9.1.1 概念 一个类有多个直接基类的继承关系称为多继承(多个父类)多继承声明语法 class 派生类名 : 访问控制 基类名1 , 访问控制 基类名2 , … , 访问控制 基类名n {数据成员和成员函数声明 };类 C 可以根据访问控制同时…...

交流约瑟夫森效应
定理 根据约瑟夫森效应的基本方程,当隧道结两端施加恒定电压V0V_0V0时,结两边超导体波函数的位相差为 Δϕ2eℏV0tΔϕ0\begin{align} \Delta\phi\frac{2e}{\hbar}V_0t\Delta\phi_0 \end{align} Δϕℏ2eV0tΔϕ0 得到超导电流密度为 JsJcs…...
大数据项目实战之数据仓库:用户行为采集平台——第3章 用户行为日志
第3章 用户行为日志 3.1 用户行为日志概述 用户行为日志的内容,主要包括用户的各项行为信息以及行为所处的环境信息。收集这些信息的主要目的是优化产品和为各项分析统计指标提供数据支撑。收集这些信息的手段通常为埋点。 目前主流的埋点方式,有代码…...
centos6下为Rstudio安装多版本R
之前的R版本太旧,不少包装不上,需要安装新版本的R: R --version R version 3.6.0 (2019-04-26) -- "Planting of a Tree"于是下载最新版R: 因为没有证书,需要加上最后面的参数. wget https://mirrors.tuna.tsinghua.edu.cn/CRAN/src/base/R-4/R-4.2.2.tar.gz --no…...

TCL 拥抱云原生,实现 IT 成本治理优化
作者:行疾 TCL 工程师团队基于阿里云企业云原生 IT 成本治理方案沉淀了一套成熟的 IT 企业成本治理流程与系统,通过阿里云容器服务提供的开箱即用的成本洞察、资源智能画像等功能,进行业务成本拆分、闲置资源可视化发现,并制定弹性…...
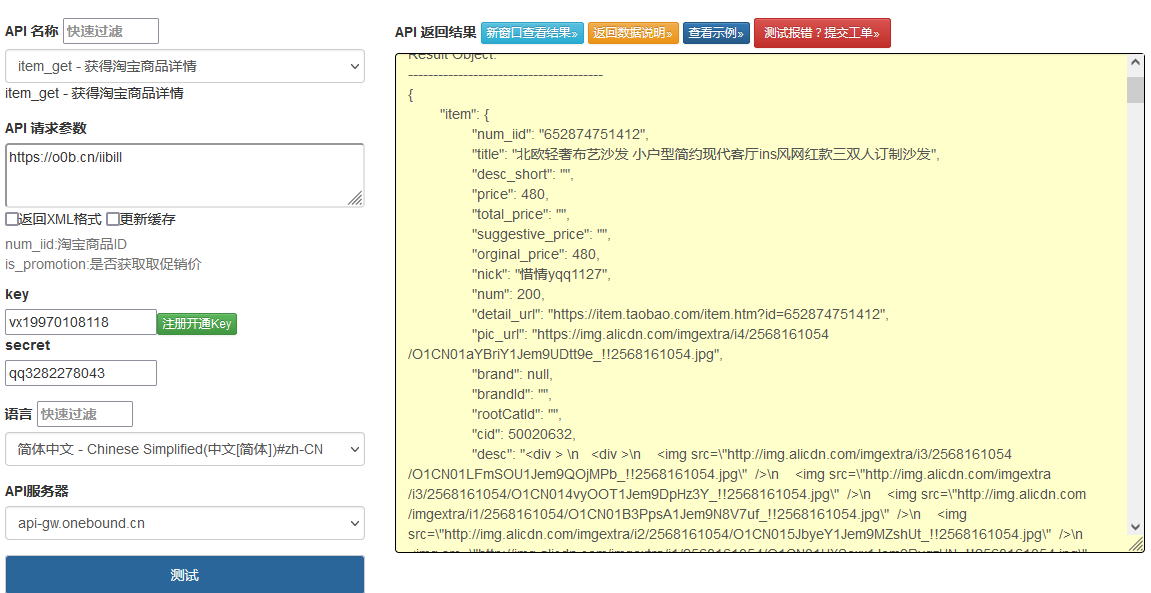
什么是API接口
API接口是指应用程序接口,是一种让不同的应用程序之间进行数据交互的方式。在现代软件开发中,API接口已经成为了必不可少的一部分。它们让开发者们可以将不同的功能组合在一起,同时也让不同的应用程序之间可以相互连接和通讯。API接口的作用A…...
基于单片机的波形发生器设计
单片机可以用来设计各种类型的波形发生器,下面是一种基于单片机的波形发生器设计方案。所需材料:单片机:可以选择常见的Atmel AVR单片机,如ATmega328P等。调制器:可以使用AD9833或AD9851等常用的调制器。时钟ÿ…...
)
phpmyadmin SQL注入 (CVE-2020-5504)
文章目录 0x01 漏洞介绍0x02 影响版本0x03 漏洞编号0x04 漏洞查询0x05 漏洞环境0x06 漏洞复现方法一:写入shell方法二:报错注入0x07 修复建议免责声明摘抄0x01 漏洞介绍 phpMyAdmin是phpMyAdmin团队的一套免费的、基于Web的MySQL数据库管理工具。该工具能够创建和删除数据库,…...
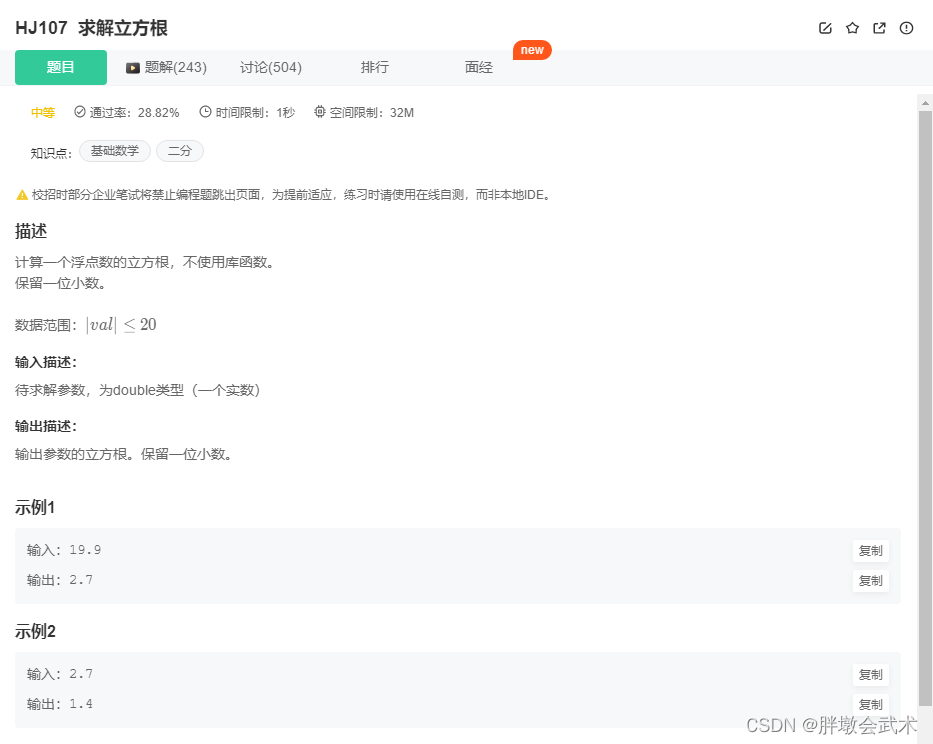
华为机试题:HJ107 求解立方根(python)
文章目录(1)题目描述(2)Python3实现(3)知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。1.1、input() 与 list(input()) 的区别、及其相互转换方…...

论文公式符号规范
参考自1,记录论文公式的符号规范: 1.变量和公式符号表达 物理量 物理量符号用英文斜体字母或希腊斜体字母,表示物理量大小用数字加单位,单位使用正体。 例如: m10.05gx10.12ζ35.36mVm10.05 \mathrm{~g} \quad x10…...

哈工大面向服务的软件系统 期末开卷提纲
引言本课程期末考试为开卷,博主2022年期末卷面94/100,总分92.9排名第2/82,现分享复习提纲以供学弟学妹们参考。本提纲仅供参考,切勿进行其他目的的使用。基于2021秋季考试题的思考一、Spring Boot的优点是:1. 非常快速…...
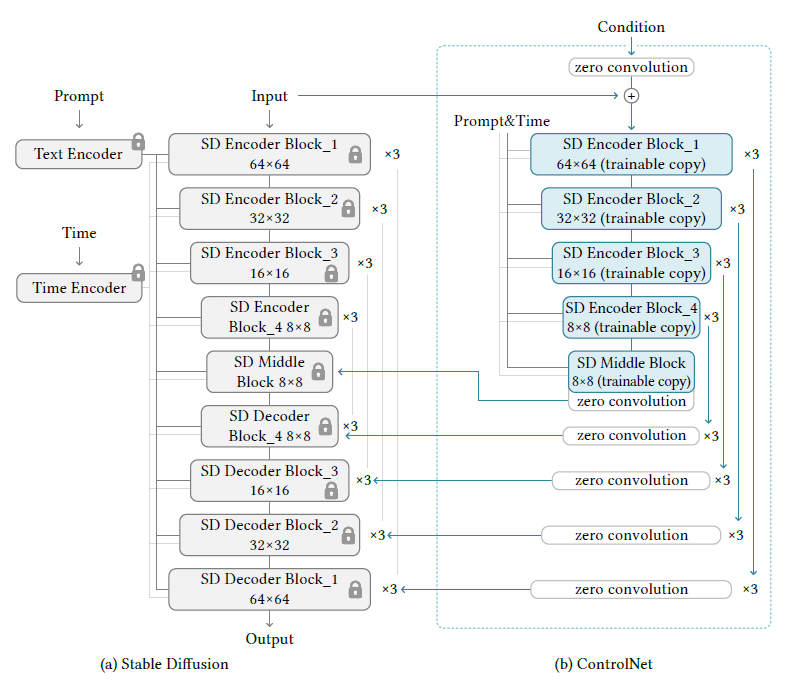
Adding Conditional Control to Text-to-Image Diffusion Models
安全验证 - 知乎知乎,中文互联网高质量的问答社区和创作者聚集的原创内容平台,于 2011 年 1 月正式上线,以「让人们更好的分享知识、经验和见解,找到自己的解答」为品牌使命。知乎凭借认真、专业、友善的社区氛围、独特的产品机制…...
C++从头再来:知识点速通
1. 关于scanf 1.1 读入数字 scanf 的返回值表示成功输入的变量个数,当输入结束时,scanf将无法再次读取数据,返回0 # include <stdio.h> # include <math.h> # include <time.h># define M 1000000; // compute the max,…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
