[蓝桥杯 2019 国 C] 数正方形
[蓝桥杯 2019 国 C] 数正方形
题目描述
在一个 N × N N \times N N×N 的点阵上,取其中 4 4 4 个点恰好组成一个正方形的 4 4 4 个顶点,一共有多少种不同的取法?
由于结果可能非常大,你只需要输出模 1 0 9 + 7 10^9 + 7 109+7 的余数。
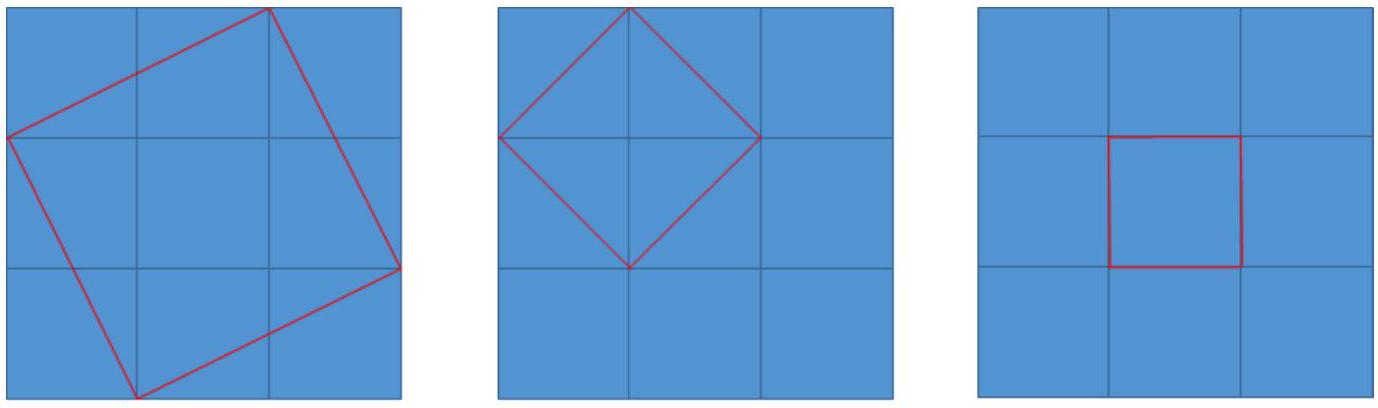
如上图所示的正方形都是合法的。
输入格式
输入包含一个整数 N N N。
输出格式
输出一个整数代表答案。
样例 #1
样例输入 #1
4
样例输出 #1
20
提示
对于所有评测用例, 2 ≤ N ≤ 1 0 6 2 ≤ N ≤ 10^6 2≤N≤106。
蓝桥杯 2019 年国赛 C 组 G 题
分析一:
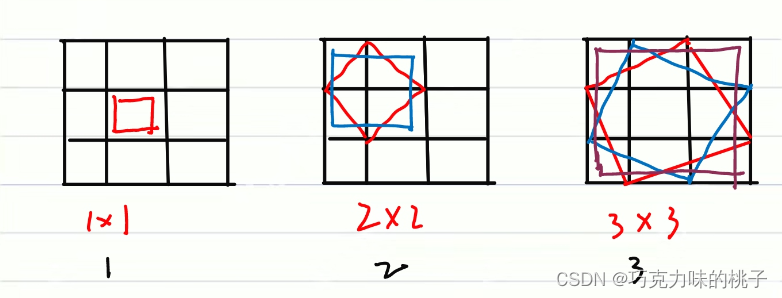
对于N*N的正方形,它放置小正方形的情况为N
分析二:
我们下一步要求题目给的N*N正方形可以分成几个1×1,2×2,3×3
(n-i+1)(n-i+1)
n:正方形的边长
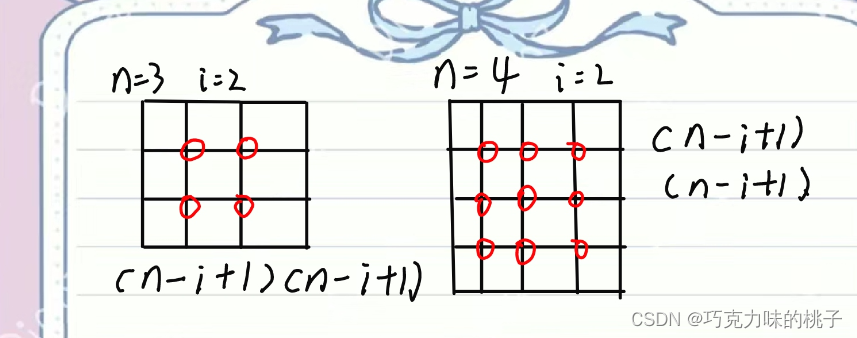
eg.对于3×3的正方形,求2×2的个数 :(3-2+1)×(3-2+1)
分析三:
题目输入的N是点数,而不是边长
边长:N-1
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n;
const int k=1e9+7;
int ans=0;
signed main()
{cin>>n;n--;for(int i=1;i<=n;i++){int m=(n-i+1)*(n-i+1);ans=(ans+m*i)%k;}cout<<ans;return 0;
}
相关文章:

[蓝桥杯 2019 国 C] 数正方形
[蓝桥杯 2019 国 C] 数正方形 题目描述 在一个 N N N \times N NN 的点阵上,取其中 4 4 4 个点恰好组成一个正方形的 4 4 4 个顶点,一共有多少种不同的取法? 由于结果可能非常大,你只需要输出模 1 0 9 7 10^9 7 1097 的…...
Redis: 配置文件详解(Redis.conf)
文章目录 一、Units二、INCLUDES三、NETWORK四、GENERAL五、SECURITY六、LIMITS 一、Units 单位,配置大小单位,开头定义了一些基本的度量单位,只支持bytes,不支持bit,大小写不敏感 二、INCLUDES 包含,多…...
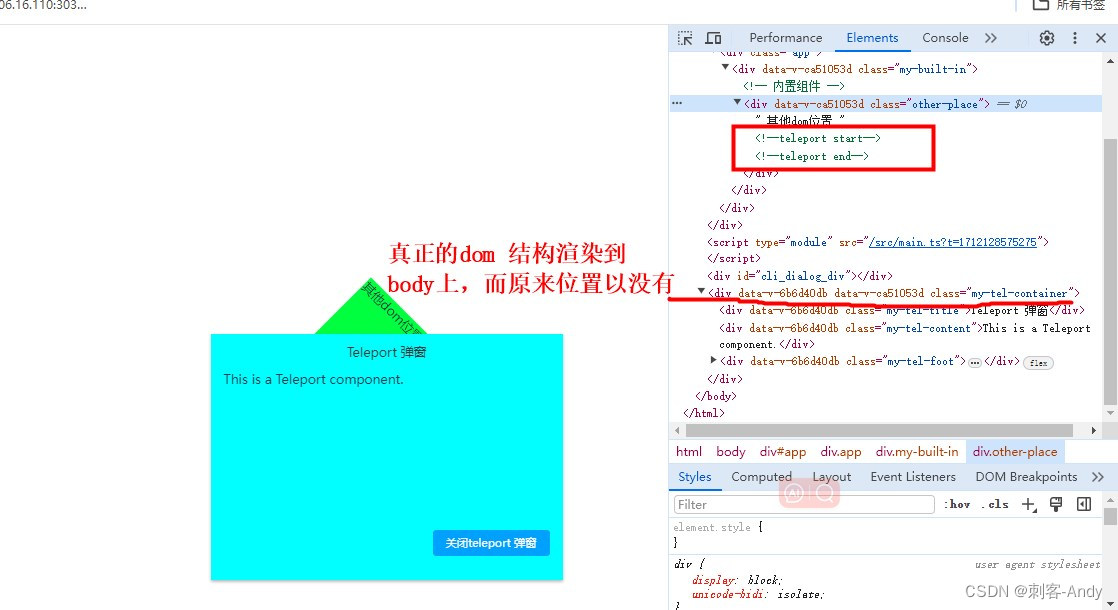
学习vue3第十四节 Teleport 内置组件介绍
<Teleport></Teleport> 作用目的: 用于将指定的组件或者元素传送到指定的位置; 通常是自定义的全局通用弹窗,绑定到 body 上,而不是在当前元素上面; 使用方法: 接收两个参数 to: 要将目标传…...

mybatis模糊查询查不到数据
排除SQL语句本身存在错误,字段名称不匹配,编码格式问题后,若使用%方式查询,一开始使用单引号查询不到数据,把改成",可以查询到数据 疑问:看别人的代码,使用单引号也可以查询到数据,原因未知...
)
Python语法总结:not(常出现错误)
0、not是什么 在python中not是逻辑判断词,用于布尔型True和False之前 a not Ture # a False b not False # b True1、not的用法 (1)判断语句 if not a:# 如果a是False,执行的语句(2)判断元素是否在…...

深入理解WebSocket:实时双向通信的利器
一、介绍 1.1 基础概念介绍 单工通信:数据传输只允许在一个方向上传输,只能一方发送数据,另一方接收数据并发送。半双工:数据传输允许两个方向上的传输,但在同一时间内,只可以有一方发送或接收数据。全双…...

Gateway是什么?(SpringCloudAlibaba组件)
1、网关介绍 **网关(Gateway)又称网间连接器、协议转换器。网关在传输层上以实现网络互连,是最复杂的网络互连设备,仅用于两个高层协议不同的网络互连。**网关的结构也和路由器类似,不同的是互连层。网关既可以用于广域网互连,也可…...

阿里巴巴拍立淘API新功能揭秘:图片秒搜商品,实现智能化个性化购物新体验
在数字化快速发展的今天,智能化和个性化已经成为购物体验中不可或缺的元素。为了满足消费者日益增长的购物需求,阿里巴巴中国站不断推陈出新,其中拍立淘API的新功能——图片秒搜商品,无疑为智能化个性化购物体验开创了新的篇章。 …...

蚓链为移动实体经济加油!
在当今数字化时代,数据已成为企业宝贵的资产之一。如何利用数据资产为可移动实体经济创造更多的增值机会呢?蚓链将为你揭示 11种行之有效的方法! 1. 个性化服务:根据客户数据,提供量身定制的产品和服务,满…...

MySQL 核心模块揭秘 | 12 期 | 创建 savepoint
回滚操作,除了回滚整个事务,还可以部分回滚。部分回滚,需要保存点(savepoint)的协助。本文我们先看看保存点里面都有什么。 作者:操盛春,爱可生技术专家,公众号『一树一溪』作者&…...
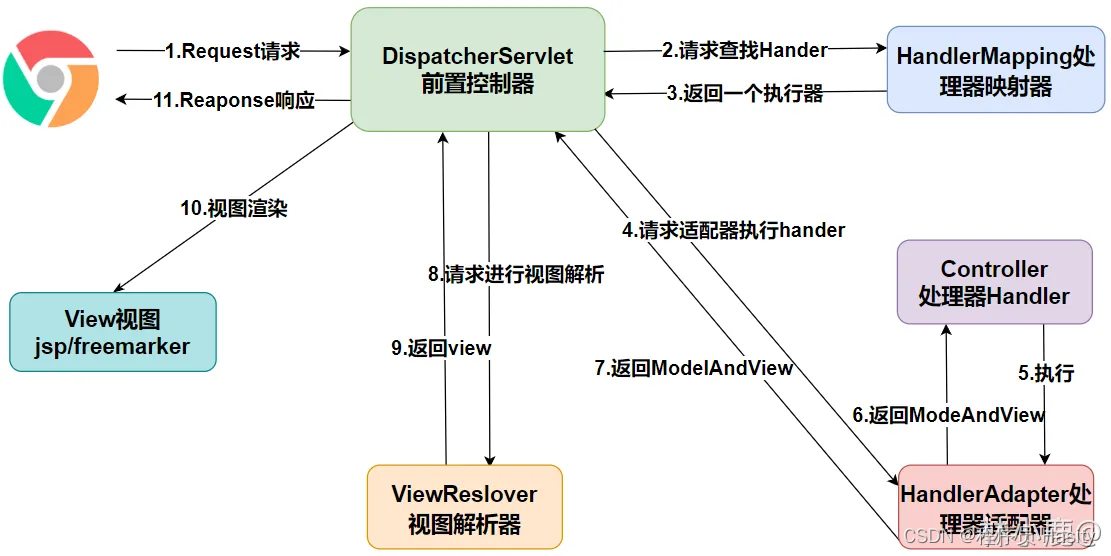
SpringMVC --- 老杜
1、什么是SpringMVC? SpringMVC是一个基于Java实现了MVC设计模式的请求驱动类型的轻量级Web框架,通过把Model,View,Controller分离,将web层进行职责解耦,把复杂的web应用分成逻辑清晰的及部分,…...
算法解决8数码问题)
详细介绍如何利用 A star(A*)算法解决8数码问题
文章目录 1. A star(A*)算法简介2. 利用A*解决8数码问题(含Python代码)2.1 什么是8数码问题2.2 A*算法中的开放列表和关闭列表2.3 A*算法解决8数码问题过程2.3.1 计算节点(棋盘顺序)间距离2.3.2 交换数字生成新的节点2.3.3 A*主求解程序1. A star(A*)算法简介 A ∗ A^*…...
如何锁定鼠标光标在水平、垂直或45度对角线模式下移动 - 鼠标水平垂直移动锁定器简易教程
在我们进行精细工作例如如创建图标和图形设计时,通常需要我们对鼠标移动进行精确控制。一旦向左或向右轻微移动,都可能导致设计出错。若出现不必要的错误,我们极有可能不得不重新开始,这会令人感到非常沮丧。这种情况下࿰…...

在 Docker 部署的 MySQL 容器内安装和使用 vim
在 Docker 部署的 MySQL 容器内安装和使用 vim 文章目录 在 Docker 部署的 MySQL 容器内安装和使用 vim步骤一:进入 MySQL 容器步骤二:更新软件源和安装 vim步骤三:验证 vim 安装步骤四:使用 vim 进行文件编辑步骤五:保…...

人工智能|深度学习——基于Xception实现戴口罩人脸表情识别
一、项目背景 近年来,随着人工智能技术的不断发展,人脸表情识别已经成为了计算机视觉领域中的重要研究方向之一。然而,在当前的疫情形势下,佩戴口罩已经成为了一项必要的防疫措施,但是佩戴口罩会遮挡住人脸的部分区域&…...

【HTML】简单制作一个动态3D正方体
目录 前言 开始 HTML部分 JS部分 CSS部分 效果图 总结 前言 无需多言,本文将详细介绍一段代码,具体内容如下: 开始 首先新建文件夹,创建两个文本文档,其中HTML的文件名改为[index.html],JS的文件名改…...
Linux 常用指令及其理论知识
个人主页:仍有未知等待探索-CSDN博客 专题分栏:http://t.csdnimg.cn/Tvyou 欢迎各位指教!!! 目录 一、理论知识 二、基础指令 1、ls指令(列出该目录下的所有子目录和文件) 语法: …...

论文阅读——Sat2Vid
Sat2Vid: Street-view Panoramic Video Synthesis from a Single Satellite Image 提出了一种新颖的方法,用于从单个卫星图像和摄像机轨迹合成时间和几何一致的街景全景视频。 即根据单个卫星图像和给定的观看位置尽可能真实地、尽可能一致地合成街景全景视频序列。…...

js怎样判断status
相信大家都知道Switch开关吧,他有两种状态,通常用1/2表示,开启时为true,关闭时为false,那么我们该怎样判断他是否为开启还是关闭你? 我们可以声明一个变量,让它等于status,判断它是否等于1/2&…...
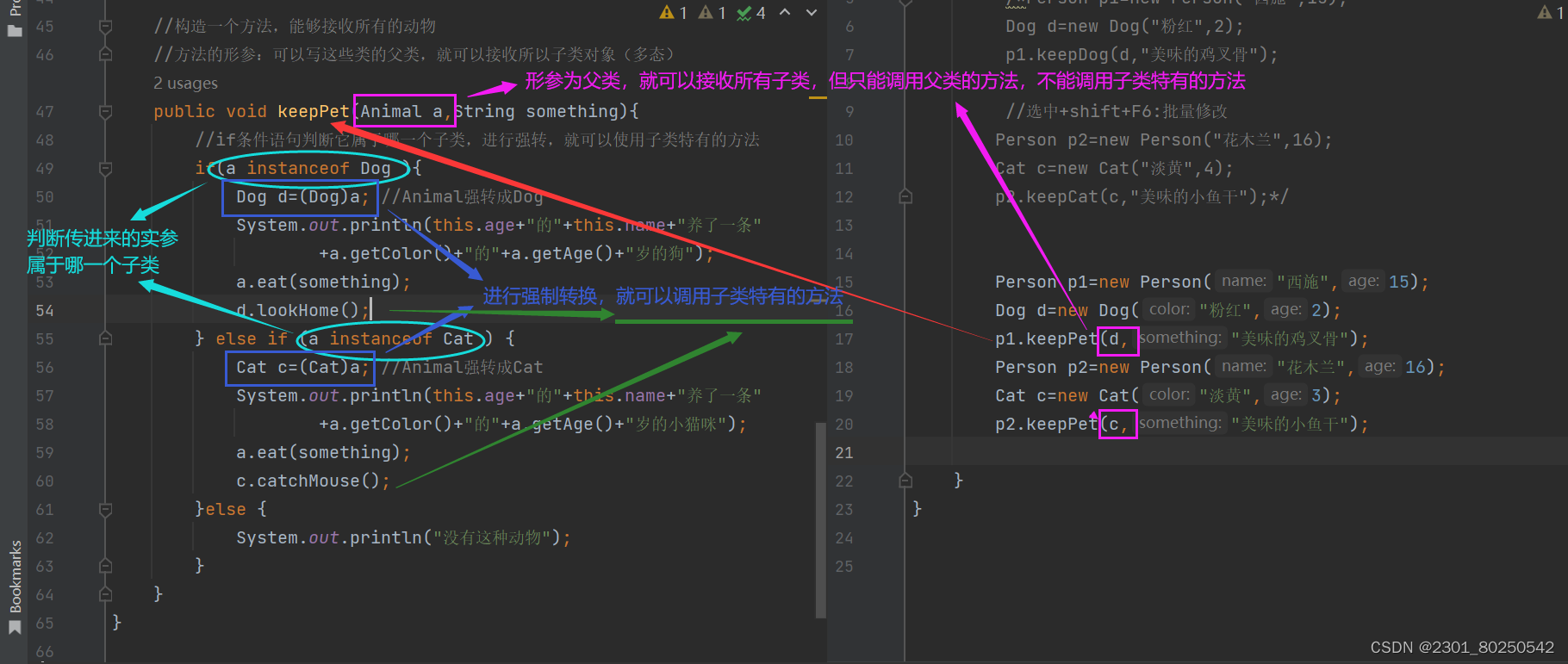
多态.Java
(1)什么是多态? 同类型的对象,表现出不同的形态。前者指父类,后者指不同的子类 说简单点,就是父类的同一种方法,可以在不同子类中表现出不同的状态,或者说在不同子类中可以实现不同…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
