【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树
22. 括号生成
数字
n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。示例 1:
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1 输出:["()"]
提示:
1 <= n <= 8
【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树
定义dfs递归函数,将叶子节点填充到ret中。
定义 ret 记录结果。
定义path表示树节点。
定义left,right表示当前树节点的左右括号数量。用来正确进入到下一个子树中。
任何情况下 left>=right必须满足才是有效的形式。
如果需要添加左括号,left<=n,left+1<=n,left<n。
如果需要添加右括号,left>=right,left>=right+1,left>right。
以上是正确进入子树的规则。
递归函数dfs内部逻辑,将path树所有叶子节点填充到ret,相当于将左子树叶子节点填充到ret,右子树叶子节点填充到ret。
if (left < n) { path.push_back('('); left++; dfs(); path.pop_back(); left--; }
这一整个代码表示左子树递归。因为是模拟树所以必须时时刻刻维护path,left,right的定义。因为这些变量都与树的定义有关。
if (left > right) { path.push_back(')'); right++; dfs(); path.pop_back(); right--; }
这一整个代码表示右子树递归。因为是模拟树所以必须时时刻刻维护path,left,right的定义。因为这些变量都与树的定义有关。
递归函数的出口,当path.size() == 2 * n,此时是叶子节点,将path添加到ret中。
class Solution {
public:int left, right;string path;vector<string> ret;int n;vector<string> generateParenthesis(int _n) {n = _n;dfs();return ret;}void dfs() {if (path.size() == 2 * n) {ret.push_back(path);return;}if (left < n) {path.push_back('(');left++;dfs();path.pop_back();left--;}if (left > right) {path.push_back(')');right++;dfs();path.pop_back();right--;}}
};77. 组合
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
示例 2:
输入:n = 1, k = 1 输出:[[1]]
提示:
1 <= n <= 20
1 <= k <= n
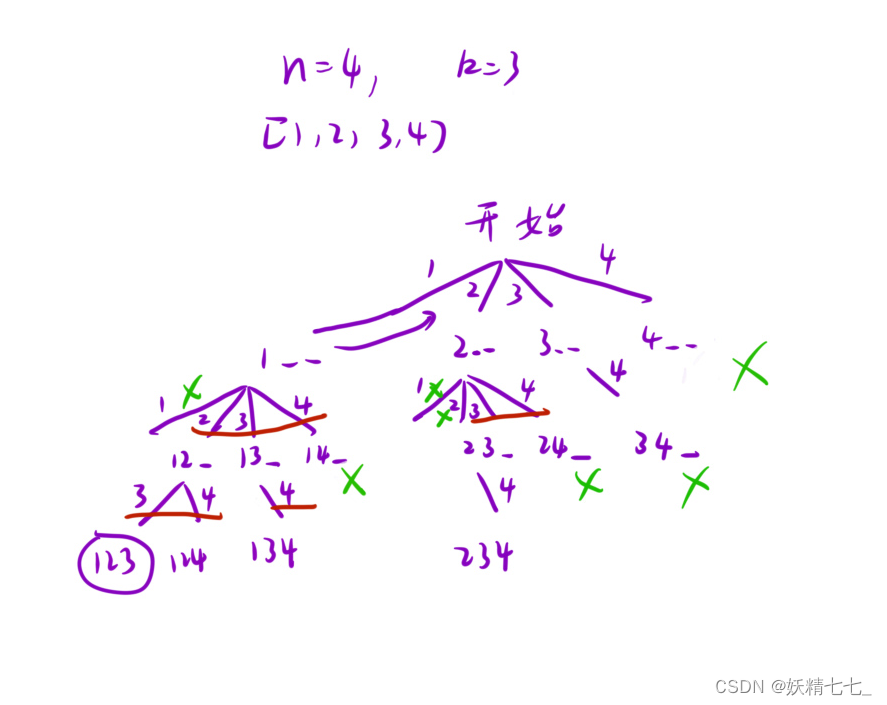
定义dfs递归函数,将path树叶子节点填充到ret中。
思考模拟树需要定义的变量。
定义path表示树的根节点。
定义pos表示子树开始遍历的下标。
定义ret记录结果。
小技巧,将n和k定义成全局变量,就不用每次都传入递归函数中。
递归函数的内部逻辑,将所有子树的叶子节点填充到 ret 中。
for (int i = pos; i <= n; i++) { path.push_back(i); int temp = pos; pos = i + 1; dfs(); path.pop_back(); pos = temp; }
for 循环中的所有代码表示一个子树的递归,用for循环变量所有的子树。
遍历下一个子树的时候,需要维护path和pos的定义。因为是模拟树所以必须时时刻刻维护path,pos的定义。因为这些变量都与树的定义有关。
递归出口,当path.size() == k时,表示是叶子节点,此时将path填充到ret中。
class Solution {
public:vector<vector<int>> ret;vector<int> path;int pos = 1;int n, k;vector<vector<int>> combine(int _n, int _k) {n = _n;k = _k;dfs();return ret;}void dfs() {if (path.size() == k) {ret.push_back(path);return;}for (int i = pos; i <= n; i++) {path.push_back(i);int temp = pos;pos = i + 1;dfs();path.pop_back();pos = temp;}}
};494. 目标和
给你一个非负整数数组
nums和一个整数target。向数组中的每个整数前添加
'+'或'-',然后串联起所有整数,可以构造一个 表达式 :
例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
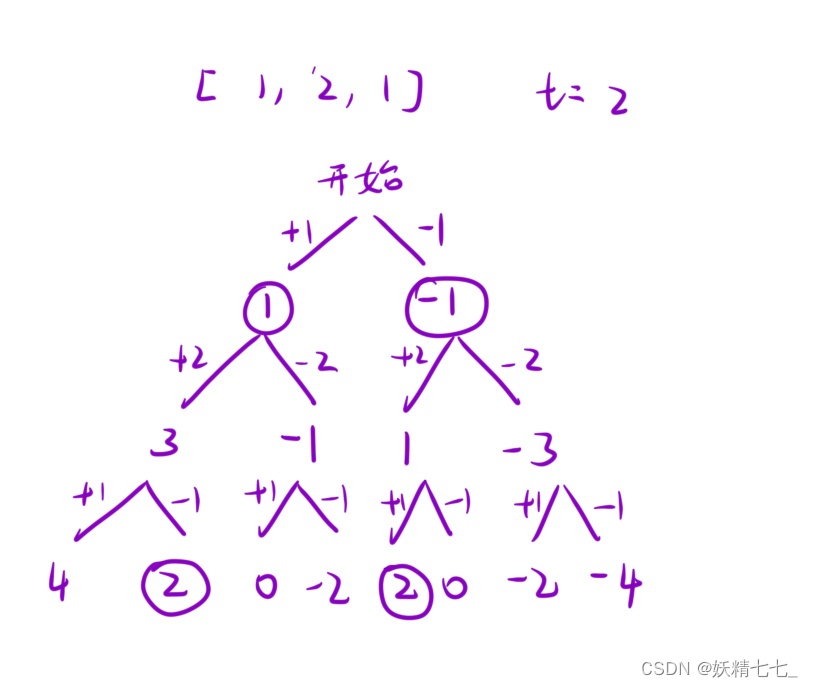
定义dfs将树叶子节点符合要求的计数。
定义path表示树根节点。
定义pos表示nums下一个应该遍历下标,也就是子树的可能性。
上面的定义模拟树。
定义ret记录结果。
定义target表示目标和,定义为全局变量。
递归函数dfs内部逻辑,将左子树叶子节点符合要求的计数,将右子树叶子节点符合要求的计数。
递归左右子树的时候需要时时刻刻维护path和pos。
path += nums[pos]; pos++; dfs(nums); pos--; path -= nums[pos];
递归左子树。因为是模拟树所以必须时时刻刻维护path,pos的定义。因为这些变量都与树的定义有关。
path -= nums[pos]; pos++; dfs(nums); pos--; path += nums[pos];
递归右子树。因为是模拟树所以必须时时刻刻维护path,pos的定义。因为这些变量都与树的定义有关。
递归函数的出口,当pos == nums.size()表示是叶子节点,同时path==target表示是符合要求的情况,此时ret++。
class Solution {
public:int ret;int path;int pos;int target;int findTargetSumWays(vector<int>& nums, int _target) {target=_target;dfs(nums);return ret;}void dfs(vector<int>& nums) {if (pos == nums.size()) {if (path == target)ret++;return;}path += nums[pos];pos++;dfs(nums);pos--;path -= nums[pos];path -= nums[pos];pos++;dfs(nums);pos--;path += nums[pos];}
};利用临时变量的性质自动维护树的定义。
此时就不需要手动维护树的定义。
手动维护树的定义需要进行操作,此时临时变量空间仅仅是int类型的,所以相对于手动维护,时间会快一点。
如果临时变量是vector类型效率可能会减低,因为每次都需要开辟vector的空间。此时用全局变量手动维护可能会更好一点。
int 类型可以不使用全局变量,利用临时变量自动维护,此时效率可能会变快。因为加减操作也是需要时间的。
class Solution {
public:int ret;int target;int findTargetSumWays(vector<int>& nums, int _target) {target = _target;dfs(nums, 0, 0);return ret;}void dfs(vector<int>& nums, int pos, int path) {if (pos == nums.size()) {if (path == target)ret++;return;}dfs(nums, pos + 1, path + nums[pos]);dfs(nums, pos + 1, path - nums[pos]);}
};结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树
22. 括号生成 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((())࿰…...

QT智能指针
一.概述 Qt智能指针是一种能够在不需要手动管理内存的情况下,自动释放资源的指针。它们是C11的std::shared_ptr的一种扩展,可以用于管理Qt对象,尤其是那些不是QObject的对象。 使用智能指针可以避免内存泄露和悬垂指针等问题,同时…...

C++笔记之pkg-config详解,以及g++、gcc编译时使用pkg-config
C++笔记之pkg-config详解,以及g++、gcc编译时使用pkg-config —— 2024-04-05 code review 文章目录 C++笔记之pkg-config详解,以及g++、gcc编译时使用pkg-config1.pkg-config详解`pkg-config` 的基本用法在 `g++`/`gcc` 编译时使用 `pkg-config`注意事项2.示例C++,普通编译…...
[Apple Vision Pro]开源项目 Beautiful Things App Template
1. 技术框架概述: - Beautiful Things App Template是一个为visionOS设计的免费开源软件(FOSS),用于展示3D模型画廊。 2. 定位: - 该模板作为Beautiful Things网站的延伸,旨在为Apple Vision Pro用户…...
 笔记)
Qt Remote Objects (QtRO) 笔记
简介 Qt Remote Objects (QtRO) 是 Qt 的一个进程间通信模块。 术语 Source 是指提供服务或提供功能供其他程序使用的对象,是 RPC 中的被调用端。 Replica 是指 Source 对象的代理对象,用于 RPC 中的调用端,对 Replica 的调用请求将被转发…...

Unity类银河恶魔城学习记录12-6.5 p128.5 Create item by Craft源代码
此章节在原视频缺失,此过程为根据源代码推断而来,并非原视频步骤 Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩…...
UE4_如果快速做出毛玻璃效果_假景深
UE4_如果快速做出毛玻璃效果_假景深 2022-08-20 15:02 一个SpiralBlur-SceneTexture材质节点完成效果,启用半透明材质通过修改BlurAmount数值大小调整效果spiralBlur-SceneTexture custom节点,HLSL语言float3 CurColor 0;float2 BaseUV MaterialFloa…...
c# wpf LiveCharts 绑定 简单试验
1.概要 c# wpf LiveCharts 绑定 简单试验 2.代码 <Window x:Class"WpfApp3.Window2"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schem…...
【Kafka】Kafka安装、配置、使用
【Kafka】安装Kafka 1. 安装Kafka2. Kafka使用2.0 集群分发脚本xsync(重要)2.0.1 scp命令2.0.2 rsync远程同步工具2.0.3 写一个集群分发脚本xsync (Shell 脚本) 2.1 Zookeeper安装2.2 对Kafka进行分发2.2.1 执行同步脚本2.2.2 三台云主机配置Kafka环境变量 1. 安装Kafka Kafka…...
2024HW-->Wireshark攻击流量分析
在HW中,最离不开的,肯定是看监控了,那么就要去了解一些wireshark的基础用法以及攻击的流量!!!! 1.Wireshark的基本用法 比如人家面试官给你一段流量包,你要会用 1.分组详情 对于我…...

Lafida多目数据集实测
Lafida 数据集 paper:J. Imaging | Free Full-Text | LaFiDa—A Laserscanner Multi-Fisheye Camera Dataset 官网数据:https://www.ipf.kit.edu/english/projekt_cv_szenen.php 官网:KIT-IPF-Software and Datasets - LaFiDa 标定数据下载&…...

excel wps中编码格式转换
EXCEL报表:另存为CSV格式,转换成UTF-8编码 - 简书 (jianshu.com) 经验证管用...

【游戏分析】非游戏领空追字符串来源
通过NPC名称找NPC数组 扫描 NPC名字 ASIC型 发现全部都有后缀 那么采用 字节集的方式去扫描 也是扫不到 说明:不是ASIC型字符串 扫描 NPC名字 Unicode型 没有结果 那么转换成字节集去扫描 终于发现结果了 把结果挨个修改字符串 发现 其中两个是可以用的 22和23 …...

golang 数组和切片
区别 1.数组长度固定,切片长度可变 2.数组是深拷贝,切片是浅拷贝,切片是引用类型 扩容规则 不同版本不一样 https://www.jb51.net/article/280481.htm#_lab2_2_1 go1.18 1.如果期望容量大于当前容量的两倍就会使用期望容量; 2.如…...
物联网实战--入门篇之(九)安卓QT--开发框架
目录 一、QT简介 二、开发环境 三、编码风格 四、设计框架 五、总结 一、QT简介 QT是一款以C为基础的开发工具,已经包含了很多常用的库,除了基本的GUI以外,还有网络、数据库、多媒体、进程通信、串口、蓝牙等常用库,开发起来…...
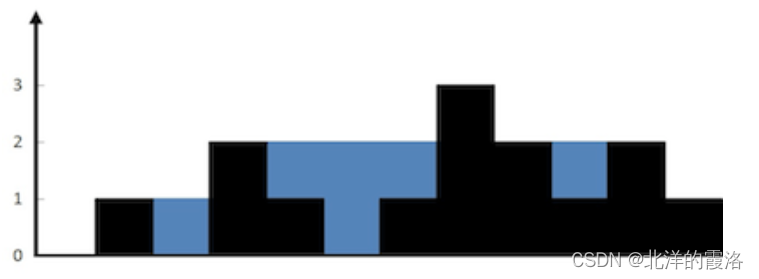
【leetcode面试经典150题】16.接雨水(C++)
【leetcode面试经典150题】专栏系列将为准备暑期实习生以及秋招的同学们提高在面试时的经典面试算法题的思路和想法。本专栏将以一题多解和精简算法思路为主,题解使用C语言。(若有使用其他语言的同学也可了解题解思路,本质上语法内容一致&…...

互联网面经
腾讯视频 代码:反转链表,单例模式 RAII,哪里用到 Web服务器怎样处理请求 get\post流程 项目使用的还是http1.0吗;http2.0:二进制、首部压缩、主动推送;Https Epoll/select/poll ET/LT 进程地址空间。3…...

xss介绍及作用
XSS(Cross-Site Scripting)是一种常见的网络安全漏洞,它允许攻击者向网站注入恶意的客户端脚本代码,从而在用户的浏览器中执行这些代码。 XSS攻击的原理是攻击者将恶意脚本插入到网页中的用户输入数据中,当其他用户访…...
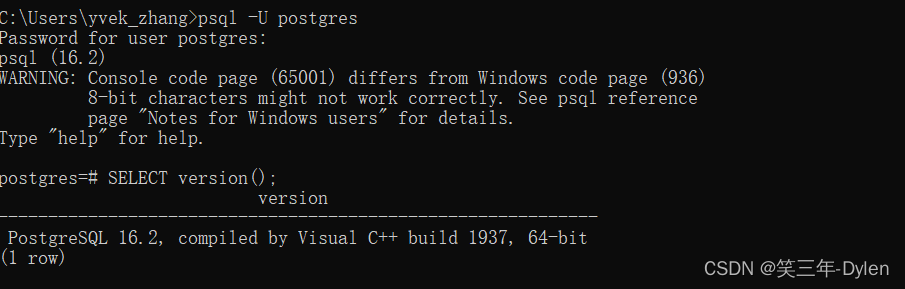
PostgreSQL入门到实战-第二弹
PostgreSQL入门到实战 PostgreSQL安装之Windows官网地址PostgreSQL概述Windows上安装PostgreSQL更新计划 PostgreSQL安装之Windows 官网地址 声明: 由于操作系统, 版本更新等原因, 文章所列内容不一定100%复现, 还要以官方信息为准 https://www.postgresql.org/PostgreSQL概…...

3-【PS让图片动起来】系列1-【导入素材】
【问题介绍】仅做图片,现在很难吸引用户视线,越来越多地图片需要动起来增添意境,比如春日樱花花瓣掉落、冬季雪花纷纷,今天来学学怎么用PS的时间轴,让图片动起来~ 如下图,一副冬日雪景图,想给画…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
