【面试经典150 | 动态规划】交错字符串
文章目录
- 写在前面
- Tag
- 题目来源
- 解题思路
- 方法一:动态规划
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【动态规划】【字符串】
题目来源
97. 交错字符串
解题思路
方法一:动态规划
首先进行特判,记字符串 s1 的长度、字符串 s2 的长度、字符串 s3 的长度分别为 m、n 和 t。如果 m + n != t,那么 s3 一定无法由 s1 和 s2 交错组成。
定义状态
在 m + n = t 时,定义 f[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 字符是否能交错组成 s3 的前 i+j 个字符。
转移关系
如果 s1 的第 i 个字符和 s3 的第 i+j 个字符相同,那么 s1 的前 i 个字符和 s2 的前 j 字符是否能交错组成 s3 的前 i+j 个字符 取决于 s1 的前 i-1 个字符和 s2 的前 j 字符是否能交错组成 s3 的前 i+j-1 个字符,即有:
KaTeX parse error: Expected 'EOF', got '&' at position 22: …j] = f[i-1][j] &̲ (s_1[i-1] == s…
同理,如果 s2 的第 j 个字符和 s3 的第 i+j 个字符相同,那么 s1 的前 i 个字符和 s2 的前 j 字符是否能交错组成 s3 的前 i+j 个字符 取决于 s1 的前 i 个字符和 s2 的前 j-1 字符是否能交错组成 s3 的前 i+j-1 个字符,即有:
KaTeX parse error: Expected 'EOF', got '&' at position 22: …j] = f[i][j-1] &̲ (s_2[j-1] == s…
base case
边界条件为 f[0][0] = true。
最后返回
最终返回 f[m][n],表示字符串 s3 是否可以右字符串 s1 和 s2 交错形成。
朴素实现代码
class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m = s1.size(), n = s2.size(), t = s3.size();if (m + n != t) return false;vector<vector<int>> f(m+1, vector<int>(n+1, false));f[0][0] = true; // base case 空字符串可以交错形成空字符串for (int i = 0; i <= m; ++i) {for (int j = 0; j <= n; ++j) {int p = i + j - 1;if (i > 0) {f[i][j] |= f[i-1][j] && (s1[i-1] == s3[p]);}if (j > 0) {f[i][j] |= f[i][j-1] && (s2[j-1] == s3[p]);}}}return f[m][n];}
};
使用滚动数组优化空间复杂度。 因为这里数组 f 的第 i 行只和第 i−1 行相关,所以我们可以用滚动数组优化这个动态规划,这样空间复杂度可以变成 O ( m ) O(m) O(m)。
空间优化代码
class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m = s1.size(), n = s2.size(), t = s3.size();if (m + n != t) return false;vector<int> f(n+1, false);f[0] = true; // base case 空字符串可以交错形成空字符串for (int i = 0; i <= m; ++i) {for (int j = 0; j <= n; ++j) {int p = i + j - 1;if (i > 0) {f[j] &= (s1[i-1] == s3[p]);}if (j > 0) {f[j] |= f[j-1] && (s2[j-1] == s3[p]);}}}return f[n];}
};
复杂度分析
时间复杂度: O ( m n ) O(mn) O(mn), m m m 为字符串 s1 的长度, n n n 为字符串 s2 的长度。
空间复杂度:按行进行滚动数组优化后的空间复杂度为 O ( m ) O(m) O(m),朴素动态规划的时间复杂度为 O ( m n ) O(mn) O(mn)。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【面试经典150 | 动态规划】交错字符串
文章目录 写在前面Tag题目来源解题思路方法一:动态规划 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行…...
:中介者模式)
设计模式(17):中介者模式
核心: 如果一个系统中对象之间的联系呈现网状结构,对象之间存在大量多对多关系,导致关系及其复杂,这些对象称为“同事对象”。我们可以引入一个中介者对象,使各个同事对象只跟中介者对象打交道,将复杂的网…...
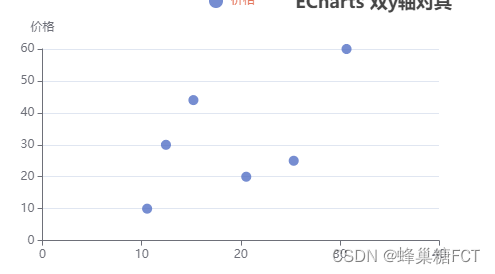
echart 折线图或散点图当横坐标为小数位时,若想显示整数该如何处理?
如图当前是这样的: 横坐标刻度目前是小数位,如果直接将小数位取整则会失去精度,所以我们要做的是刻度即是整数,又能显示小数位对应的数值; 思路就是直接手动设置刻度:设置xAxis的min,max,splitNumber,同时不…...
一套C#自主版权+应用案例的手麻系统源码
手术麻醉信息管理系统源码,自主版权应用案例的手麻系统源码 手术麻醉信息管理系统包含了患者从预约申请手术到术前、术中、术后的流程控制。手术麻醉信息管理系统主要是由监护设备数据采集子系统和麻醉临床系统两个子部分组成。包括从手术申请到手术分配,…...
31.2k star, 免费开源的白板绘图工具 tldraw
31.2k star, 免费开源的白板绘图工具 tldraw 分类 开源分享 项目名: tldraw -- 无限画布白板 Github 开源地址: https://github.com/tldraw/tldraw 在线测试地址: tldraw 文档地址: tldraw SDK tldraw 是一款开源免费的无限画布白板&…...
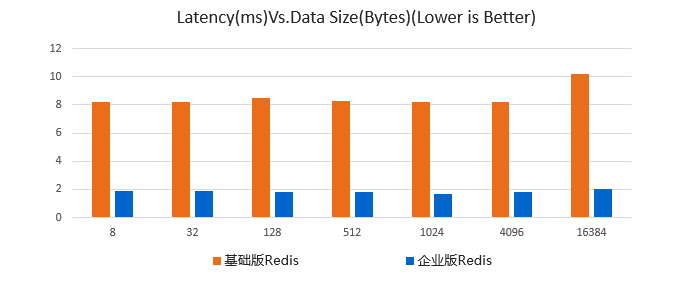
Redis开源协议调整,我们怎么办?
2024年3月20日, Redis官方宣布,从 Redis 7.4版本开始,Redis将获得源可用许可证 ( RSALv2 ) 和服务器端公共许可证 ( SSPLv1 ) 的双重许可,时间点恰逢刚刚完成最新一轮融资,宣布的时机耐人寻味。 Redis协议调整,对云计算…...

干了三年外包。。。忘了什么是CICD。。。
干了三年外包。。。忘了什么是CICD。。。 CI/CD(持续集成与持续交付) 是一种软件开发实践,它可以帮助我们更快地交付高质量的软件产品。CI/CD的核心思想是将软件开发过程中的各个阶段自动化,从而减少人工干预,提高开发效率和产品质量。本文将…...

【LeetCode】454. 四数相加 II
目录 题目 思路 代码 题目 题目链接:. - 力扣(LeetCode) 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1…...
)
搜索(DFS BFS)
DFS 常规DFS: 二叉树前序,中序,后序遍历-CSDN博客 void postorderTraversal(root)初始化一个空列表 arrfind访问总树(root,arr)return arrvoid find(temp, arr)if temp 为空return // 调用顺序由前中后序决定find递归访问左子树find递归访问右子树arr加入当前节点…...

koc和kol是什么意思?
一、koc和kol是什么意思? koc和kol是专业术语。KOC是关键意见消费者的意思,是Key Opinion Consumer的缩写;KOL是关键意见领袖的意思,是Key Opinion Leader的缩写。 1、关键意见领袖kol “关键意见领袖”通俗地讲是达人。这些人…...
基于vscode Arduino插件开发Arduino项目
基于vscode Arduino插件开发arduino项目 插件配置问题记录1. 指定编译输出文件夹2. 编译下载时不输出详细信息3. 输出端口信息乱码4. 通过串口输出中文,vscode对应的串口助手上会显示乱码(未解决) 插件配置 环境:Arduino插件版本…...
AI 驱动强大是视频转换处理软件
由 AI 驱动的视频工具包。 增强、转换、录制和编辑视频AI 驱动的顶级视频工具包。 不论是老旧、低质、噪声或模糊的影片/图像,都能升级至 4K,稳定抖动的影片,提升帧率至 120/240fps,并能以全面 GPU 加速进行转换、压缩、录制和编辑…...
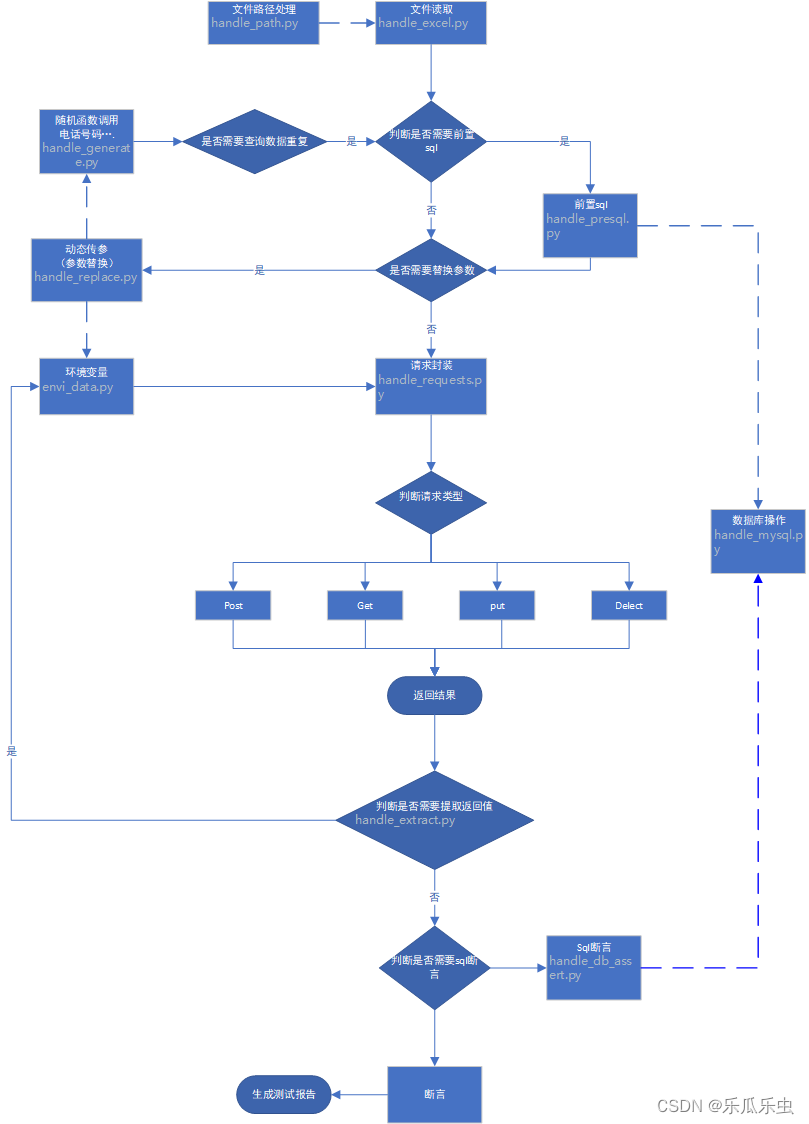
Python+requests+Pytest+logging+allure+pymysql框架详解
一、框架目录结构 1)tools目录用来放公共方法存储,如发送接口以及读取测试数据的方法,响应断言 数据库断言 前置sql等方法;2)datas目录用例存储接口用例的测试数据,我是用excel来存储的数据,文件数据 图片数据等;3)testcases目录用来存放测试用例,一个python文件对应…...

菜鸟笔记-Numpy函数-full/random.randint/random.choice
full函数 numpy.full 是 NumPy 库中的一个函数,它用于创建一个具有指定形状、数据类型和填充值的数组。此函数非常有用,因为它允许你快速生成一个具有相同值的数组,而无需手动设置每个元素。 1函数介绍 numpy.full(shape, fill_value, dty…...
)
蓝桥杯每日一题:牛的学术圈I(二分,双指针)
由于对计算机科学的热爱,以及有朝一日成为 「Bessie 博士」的诱惑,奶牛 Bessie 开始攻读计算机科学博士学位。 经过一段时间的学术研究,她已经发表了 N篇论文,并且她的第 i 篇论文得到了来自其他研究文献的 ci次引用。 Bessie 听…...

fping命令
fping是一个用于网络扫描的工具,它可以在 Linux 系统上使用。fping可以发送 ICMP ECHO_REQUEST(即 ping)数据包到指定的网络地址范围,并等待响应。通过这种方式,fping可以用来检测哪些 IP 地址是活跃的。 可以测试多个…...

奇富科技推出新一代全自研智能语音模型,打破沟通壁垒
“您好!请问是李先生噻?” 李先生刚接起电话,就被这熟悉的乡音逗乐了。这不是他所预料的常规客服,而是奇富科技新一代全自研智能语音模型——QI语精灵。这款模型不仅能用方言与人自然交流,还能在智能营销、贷后提醒、风…...

穿越代码之海:探寻结构体深层逻辑,展望未来应用新天地
欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看,已成习惯 创作不易,多多支持! 结构体作为一种数据结构,其定义和特点决定了它在各种应用中的广泛适用性。随着科技的进步和新兴行业的不断涌现…...

layui框架实战案例(26):layui-carousel轮播组件添加多个Echarts图标的效果
在Layui中,使用layui-carousel轮播组件嵌套Echarts图表来实现多个图表的展示。 css层叠样式表 调整轮播图背景色为白色;调整当个Echarts图表显示loading…状态;同一个DIV轮播项目添加多个Echarts的 .layui-carousel {background-color: #f…...
Unity开发一个FPS游戏之三
在前面的两篇博客中,我已实现了一个FPS游戏的大部分功能,包括了第一人称的主角运动控制,武器射击以及敌人的智能行为。这里我将继续完善这个游戏,包括以下几个方面: 增加一个真实的游戏场景,模拟一个废弃的…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
