使用 Docker 部署 Photopea 在线 PS 工具
1)Photopea 介绍

GitHub:https://github.com/photopea/photopea
官方手册:https://www.photopea.com/learn/
Adobe 出品的「PhotoShop」想必大家都很熟悉啦,但是「PhotoShop」现在对电脑配置要求越来越高,体积越来越大,这对于轻量办公配置的电脑/笔记本来说就非常吃力了。
特别是偶尔外出临时急需用「PhotoShop」来改改文件啥的,手头如果没有电脑、笔记本,这就很麻烦了,甲方爸爸估计会喊你去网吧整了。
又或者 Linux 用户需要修改 PSD 格式的图片,而「PhotoShop」是没有推出 Linux 版的,这就显得很尴尬,只能用 Wine 来运行一个旧版的「PhotoShop」或者通过虚拟机的方式。
所以有国外网友( 捷克 90 后的程序员 )自制一款在线版的 “PhotoShop”,虽然不是 Adobe 官方出品,却有官方内味。其实在线版的图像编辑工具有很多,但很多都不支持 PSD 格式,而这款「Photopea」就完美兼容支持 PSD 格式。
最重要的是只要有现代的浏览器就可以支持:Chrome、Safari 等。支持 PC、手机、IPad 等设备,打开浏览器,输入 Photopea 官网地址即可打开使用,支持中文、英文、日文等多国语言,免费使用,功能全开放。
2)Photopea 功能
- 图像编辑
- 图像修饰
- 图层管理
- 特效滤镜管理
- 多种格式导出
3)Photopea 在线体验
Demo:https://www.photopea.com/
Photopea 的操作界面跟 Photoshop 基本上相同,利用这款工具,你可以在自由环境下处理云盘和 U 盘中的 PSD 文件,也可以通过它将 PSD 和 SKETCH 文件自由转换。Photopea 的 UI 界面和 PS 几乎一模一样,同样的深灰色调,同样的 icon 排列,同样的画板,右边和 PS 一样有图层、操作历史工具栏,这个布局对 PS 用户可以说非常友好了,没有什么学习难度。除了交互类似之外,快捷键也基本一样。新软件完全免费,并透过浏览器运行,Photopea 支援大多数主流文件格式,包括:JPG、GIF 和 PSD。最重要的是,Photopea 支持图层、图层蒙版、图层混合模式、笔擦等等功能,用家可以轻松地完成较复杂的图像编辑工作。当然,高阶的 Photoshop 功能这软件暂时仍未能提供。

4)检查 Docker 环境
4.1)安装 Docker 软件
# 高版本 Docker 安装
curl -fsSL https://get.docker.com/ | sh
# 关闭防火墙
systemctl disable --now firewalld
setenforce 0
# 启用 Docker
systemctl enable --now docker
4.2)检查 Docker 服务
systemctl status docker

4.3)开启 IPv4 forwarding
echo "net.ipv4.ip_forward=1" >> /etc/sysctl.conf
systemctl restart network
sysctl net.ipv4.ip_forward
5)安装 Docker-compose
5.1)下载 Docker-Compose 软件包
curl -L https://github.com/docker/compose/releases/download/v2.2.2/docker-compose-linux-x86_64 -o /usr/local/bin/docker-compose
5.2)Docker-Compose 增加执行权限
chmod +x /usr/local/bin/docker-compose
5.3)检查 Docker-Compose 版本
docker-compose -v
6)下载 Photopea 镜像
1) 创建存放 Photopea 的路径
mkdir /docker/Photopea -p && cd /docker/Photopea2) 该镜像已上传至个人的阿里云镜像站点
docker pull registry.cn-guangzhou.aliyuncs.com/os_cmty/os_cmty:Photopea3) 运行 Photopea 容器
docker run -d --name Photopea -p 2000:2887 registry.cn-guangzhou.aliyuncs.com/os_cmty/os_cmty:Photopea
镜像导出:# 导出镜像docker save 04dbf135916e > Photopea.tar# 上传云盘https://www.alipan.com/s/BJFzsHM67nM# 后续 载入 镜像$ docker load < Photopea.tar
检查容器运行状态
docker ps -a

7)访问 Photopea 页面
访问 Photopea 首页 访问地址:http://服务器IP地址:2000

8)总结
Photopea 适合所有需要进行图片编辑的人群,无论是专业的设计师还是普通用户。它的界面与 Photoshop 非常相似,对于有 PS 基础的用户来说,可以快速上手并开始使用。而对于那些只需要进行简单修图的人,Photopea 提供了便捷的在线编辑功能,无需下载安装任何软件。
相关文章:

使用 Docker 部署 Photopea 在线 PS 工具
1)Photopea 介绍 GitHub:https://github.com/photopea/photopea 官方手册:https://www.photopea.com/learn/ Adobe 出品的「PhotoShop」想必大家都很熟悉啦,但是「PhotoShop」现在对电脑配置要求越来越高,体积越来越大…...

回溯法(一)——全排列 全组合 子集问题
全排列问题 数字序列 [ l , r ] [l,r] [l,r]区间内元素的全排列问题 extern int ans[],l,r,num;//num:方案数 extern bool flag[]; void dfs(int cl){//cl:current left,即为当前递归轮的首元素if(cl r 1){//数组已越界,本轮递归结束for…...
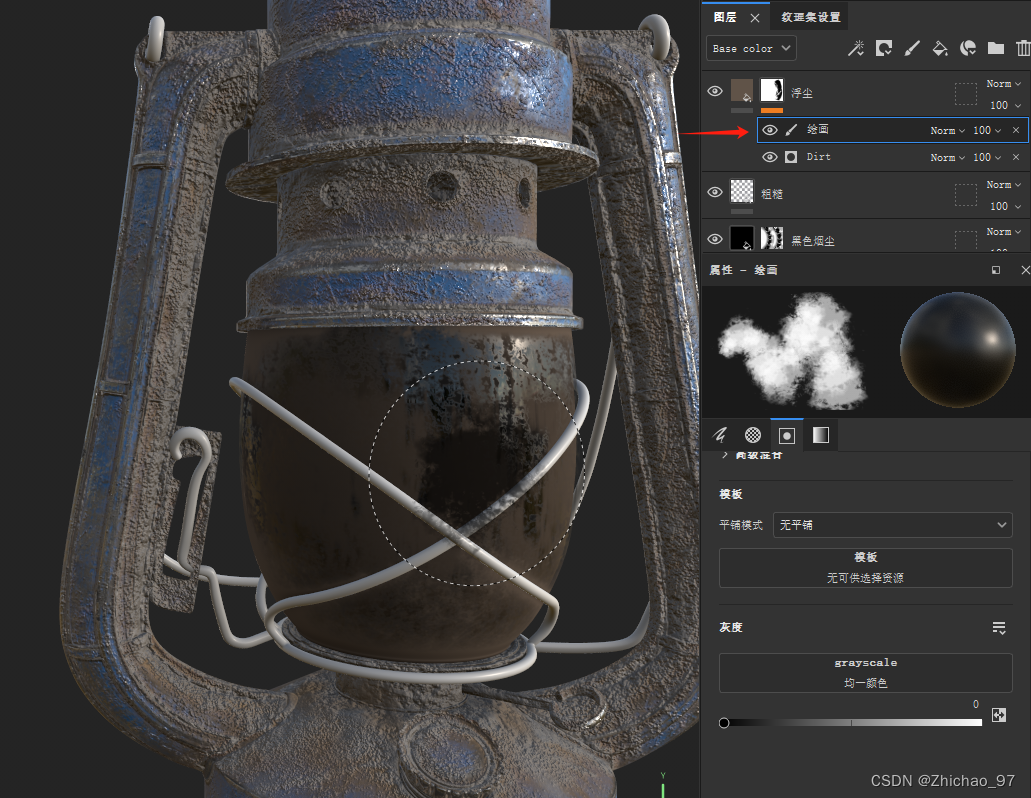
【Pt】马灯贴图绘制过程 04-玻璃脏迹
目录 效果 步骤 一、透明玻璃 二、烟熏痕迹 三、粗糙 四、浮尘 效果 步骤 一、透明玻璃 1. 打开纹理集设置,着色器链接选择“新的着色器链接” 在着色器设置中可以看到此时名称为“Main shader (Copy)” 这里修改名称为“玻璃” 在…...

Rust 程序设计语言学习——枚举模式匹配
枚举(enumerations),也被称作 enums。match 允许我们将一个值与一系列的模式相比较,并根据相匹配的模式执行相应代码。 1 枚举的定义 假设我们要跨省出行,有多种交通工具供选择。常用的交通工具有飞机、火车、汽车和轮…...

正则表达式(1)
文章目录 专栏导读1、match2、匹配目标3、通用匹配4、常用匹配规则表格 专栏导读 ✍ 作者简介:i阿极,CSDN 数据分析领域优质创作者,专注于分享python数据分析领域知识。 ✍ 本文录入于《python网络爬虫实战教学》,本专栏针对大学生…...

nginx + keepalived 搭建教程
1.安装依赖 yum install -y keepalived systemctl start keepalived systemctl enable keepalived 2.配置 a. keepalived.conf配置 global_defs {router_id nginx_server2 # 机器标识(backup节点为nfs_server2) }vrrp_script chk { script "/etc/keepalived/check_po…...

React事件和原生事件的执行顺序
在 React 中,事件处理分为两种类型:React 合成事件(Synthetic Event)和原生 DOM 事件(Native DOM Event)。它们的执行顺序略有不同。 React 合成事件 React 合成事件的执行顺序: React 合成事件…...

为什么在计算查询Q和键K的矩阵乘法时需要转置键矩阵K。示例说明q11,k11代表什么。线性变换矩阵 W_q 用于生成查询,W_k 用于生成键怎么获取的。
目录 为什么在计算查询Q和键K的矩阵乘法时需要转置键矩阵K。 示例说明q11,k11代表什么。...

剑指Offer题目笔记27(动态规划单序列问题)
面试题89: 问题: 输入一个数组表示某条街道上的一排房屋内财产的数量。相邻两栋房屋不能同时被盗,问小偷能偷取到的最多财物。 解决方案一(带缓存的递归): 解决方案: 由于有报警系统&…...

撸代码时,有哪些习惯一定要坚持?
我从2011年开始做单片机开发,一直保持以下撸代码的习惯。 1.做好代码版本管理 有些人,喜欢一个程序干到底,直到实现全部的产品功能,我以前做51单片机的项目就是这样。 如果功能比较多的产品,我不建议这样做࿰…...
)
【leetcode面试经典150题】17.罗马数字转整数(C++)
【leetcode面试经典150题】专栏系列将为准备暑期实习生以及秋招的同学们提高在面试时的经典面试算法题的思路和想法。本专栏将以一题多解和精简算法思路为主,题解使用C语言。(若有使用其他语言的同学也可了解题解思路,本质上语法内容一致&…...
前后端开发之——文章分类管理
原文地址:前后端开发之——文章分类管理 - Pleasure的博客 下面是正文内容: 前言 上回书说到 文章管理系统之添加文章分类。就是通过点击“新建文章分类”按钮从而在服务端数据库中增加一个文章分类。 对于文章分类这个对象,增删改查属于配…...
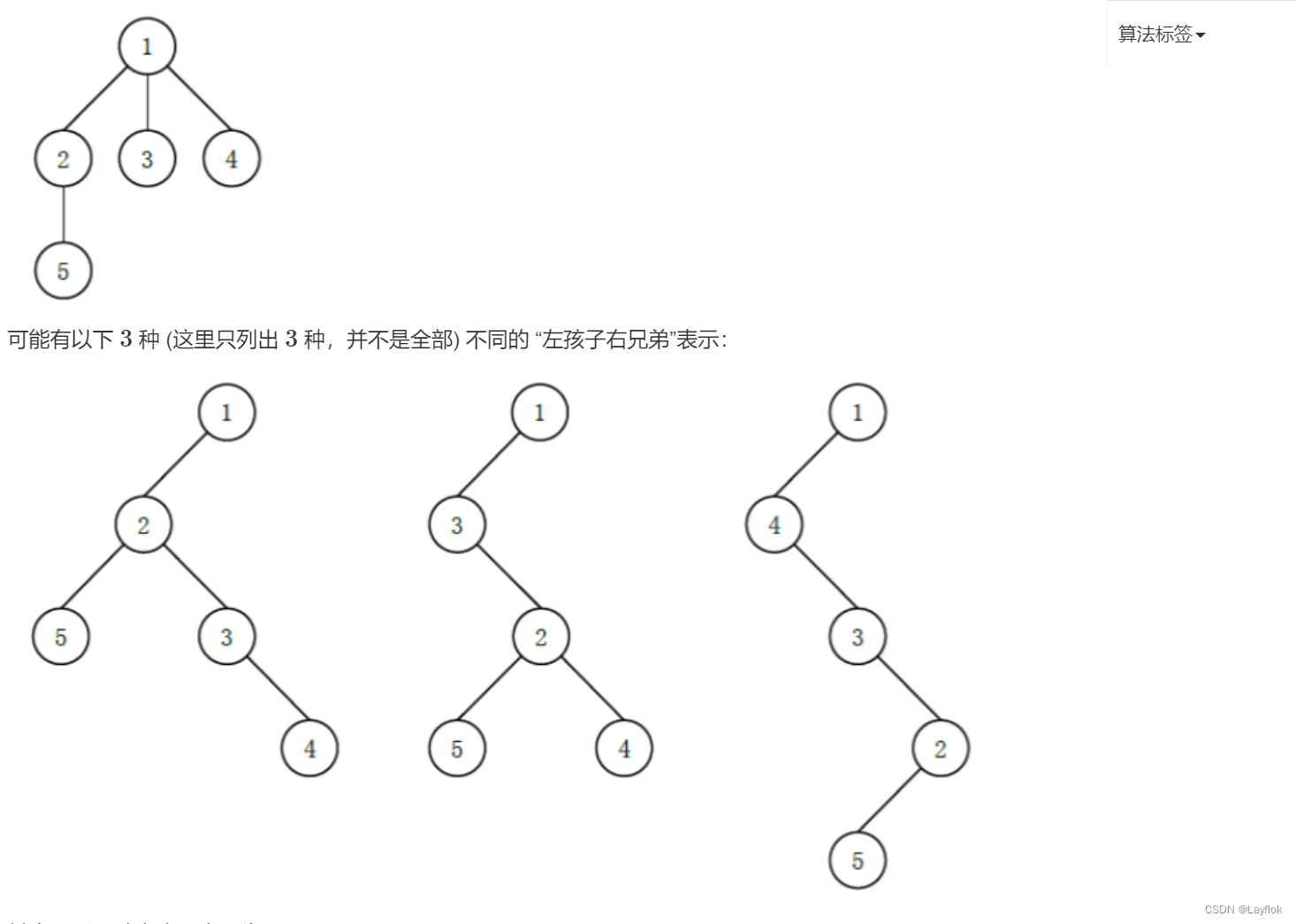
第12届蓝桥杯省赛 ---- C/C++ C组
文章目录 1. ASC2. 空间3. 卡片4. 相乘5. 路径6.时间显示7.最少砝码8. 杨辉三角形9. 左孩子右兄弟 第12届蓝桥杯省赛,C/C C组真题,第10题不是很清楚,题解不敢乱放😁😁😁 1. ASC 额。。。。 #include <i…...
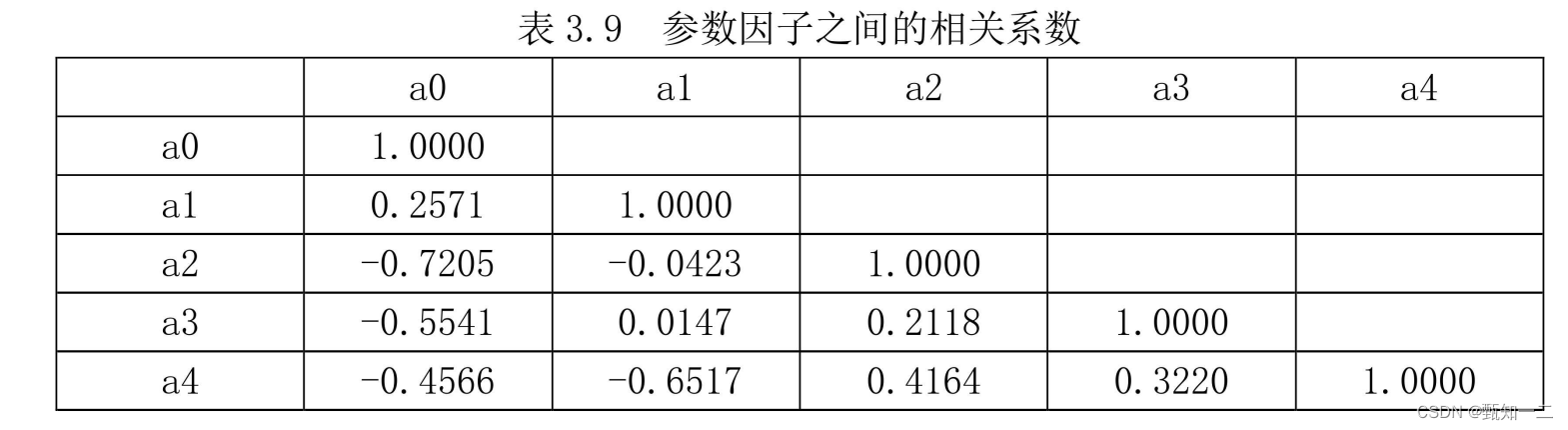
IVS模型解释
核心思路 【Implied volatility surface predictability: The case of commodity markets】 半参数化模型:利用各种参数(或者因子)对隐含波动率进行降维(静态参数化因子模型),对参数化因子的时间序列进行间接的建模 基于非对称…...

通用开发技能系列:Git
云原生学习路线导航页(持续更新中) 本文是 通用开发技能系列 文章,主要对编程通用技能Git进行学习 1.为什么使用版本控制系统 版本控制系统可以解决的问题 代码备份很重要版本控制很重要协同工作很重要责任追溯很重要 常见的版本控制系统 Gi…...
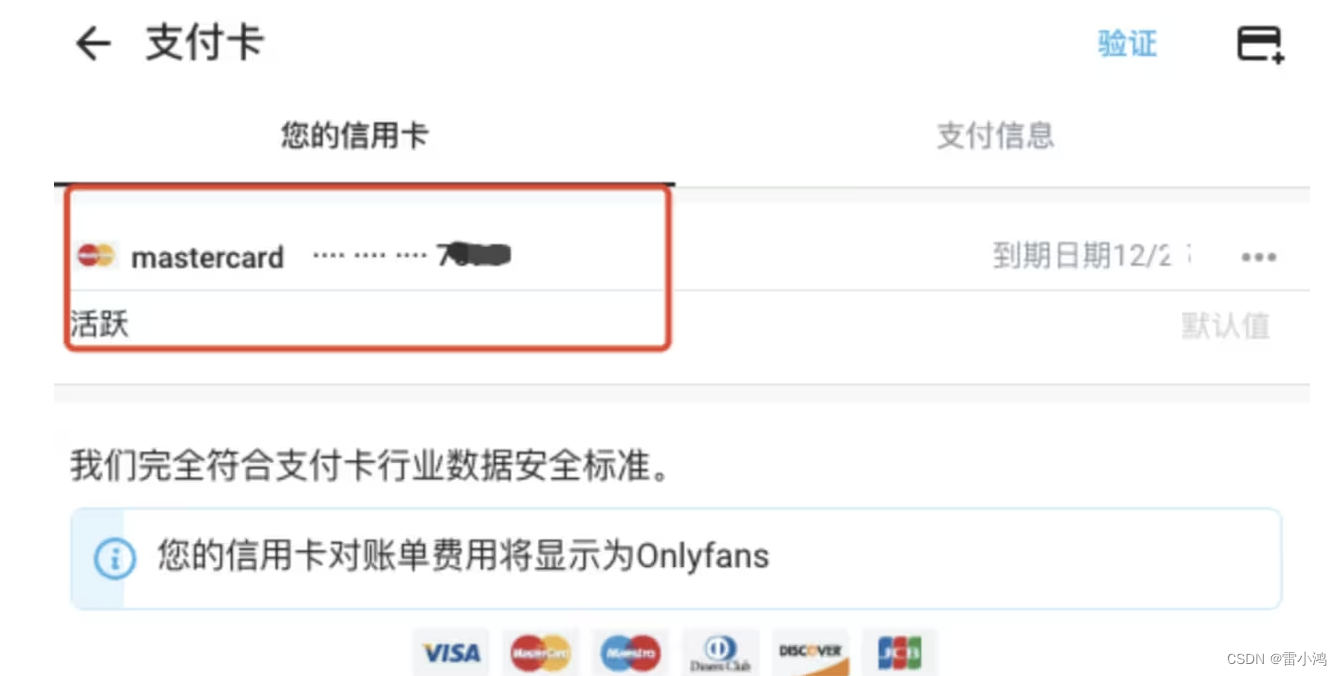
最新怎么订阅OnlyFans上喜欢的博主,详细教程
大家好,本文教大家如何用虚拟信用卡在 Onlyfans 订阅,链接在浏览器打开地址https://bewildcard.com/i/GPT310,虚拟卡开好之后,用支付宝充值就可以进行订阅OnlyFans平台的博主了。 什么是OnlyFans? OnlyFans 是一个提…...
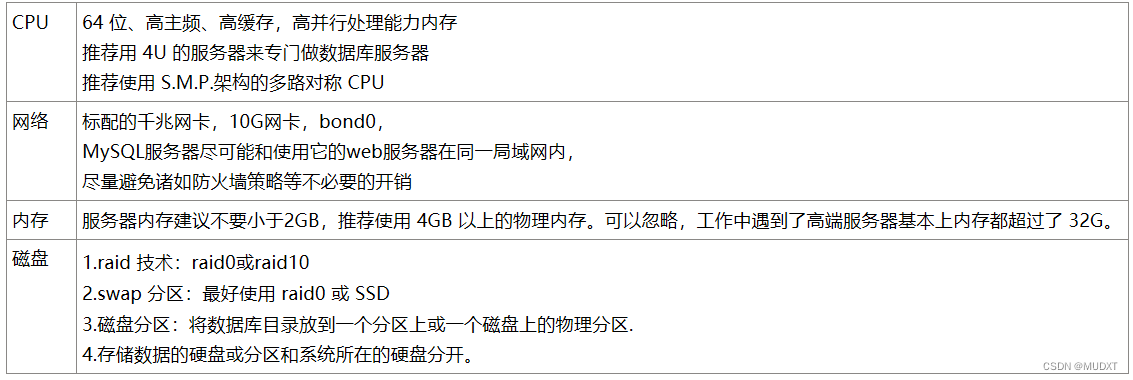
Mysql故障和优化
一、MySQL故障 二、MySQL优化 1.硬件优化: 2.数据库设计与规划 1.提前估计数据量,使用什么存储引擎 2.数据库服务器专机专用,避免额外的服务可能导致的性能下降和不稳定性 3.增加多台服务器,以达到稳定、高效的效果。主从同步、…...
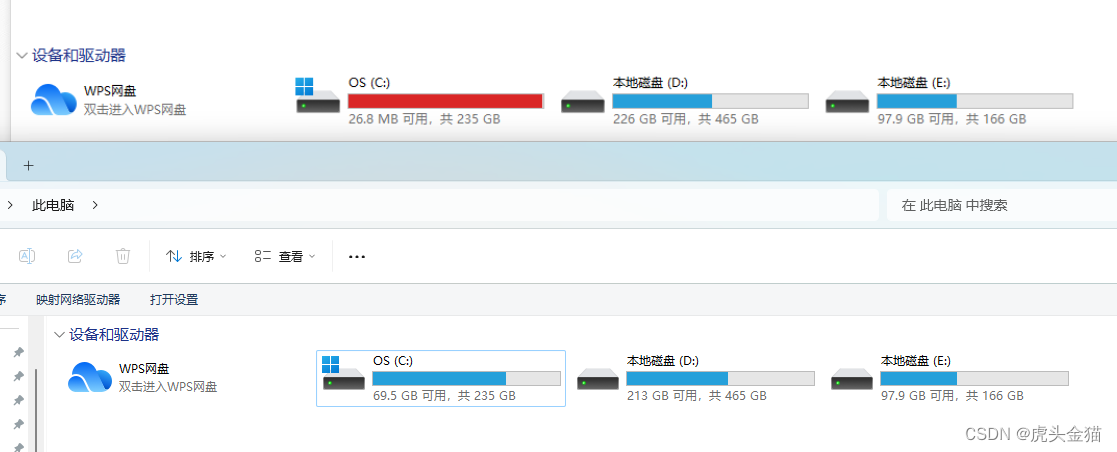
Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理
Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理 文章目录 Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理磁盘清理工具 使用“运行”命令访问磁盘清理利用存储感知自动管理空间清理WinSxS文件夹结合手动清理策略 小结删除临时文件总结&…...

14届蓝桥杯 C/C++ B组 T7 子串简写 (字符串)
采用存储目标字符下标的方法,此题的想法比较新奇,故予以记录。 存好下标之后,可以先定位好启始的字符,然后去搜结尾字符符合长度k并且最靠近启始字符的下标,找到之后可以直接取到这个下标之后的所有下标,因…...
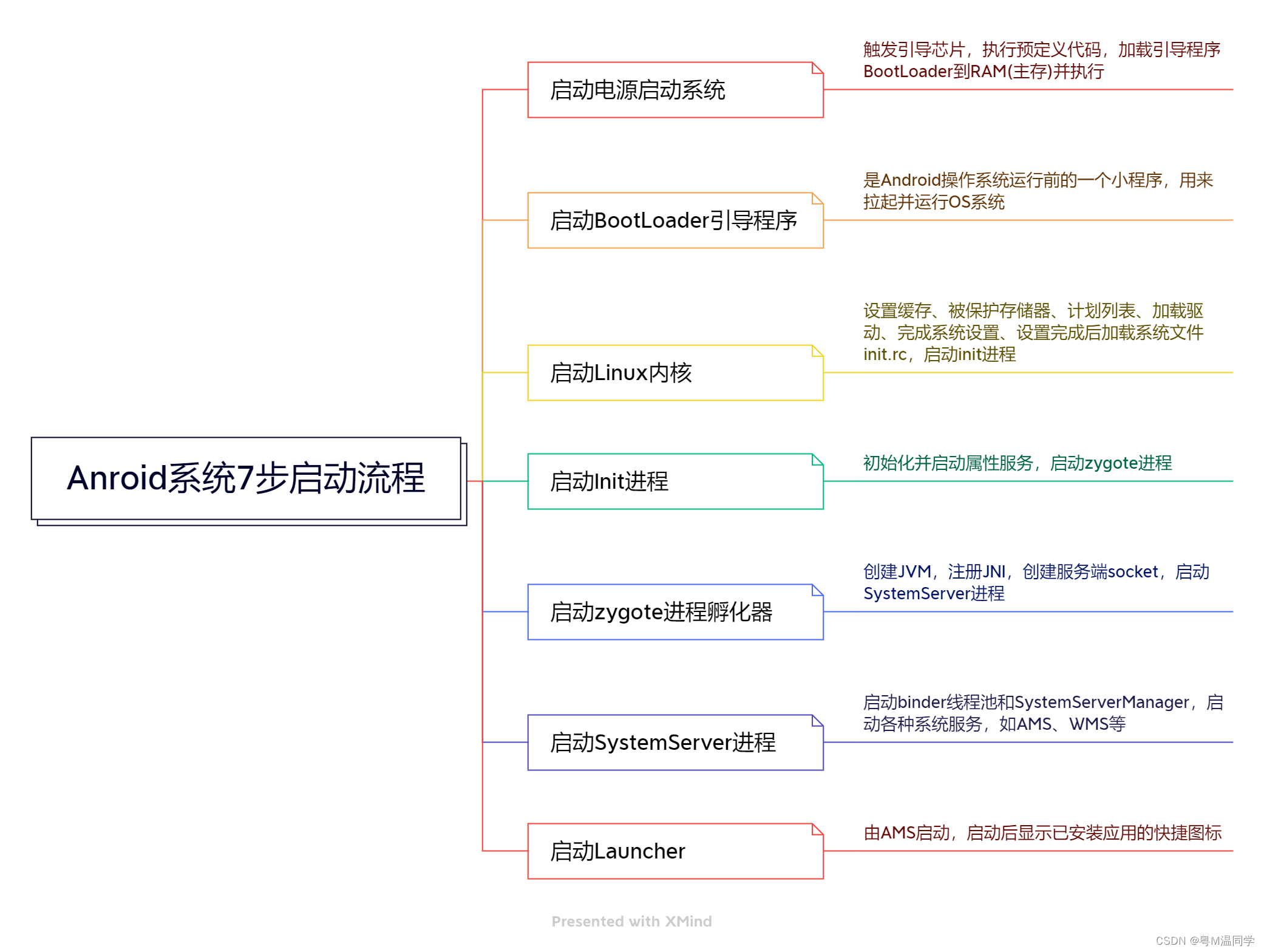
Android 系统大致启动流程
Android启动流程大体为:BootRom -> BootLoader -> Kernel -> Init -> Zygote -> SystemServer ->Launcher 1、Loader层 1.1、Boot ROM 电源按下,引导芯片代码开始从预定义的地方(固化在ROM)开始执行࿰…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
