挑战30天C++基本入门(DAY8--树)[part 3](速通哦~)
#上一章我们把搜索二叉树的知识给传授完毕,如果认真的看下去并且手打了几遍,基本上内部的逻辑还是可以理解的,那我们现在就截至继续学习树的一些重要知识啦~~
树高怎么求呀?如果用上一次学的层次遍历来求树高,有点小题大做了,这章我们就教大家如何用递归来求树高。
如何查找树里的元素呢??
哈夫曼树是个啥子??
在这一章节我都会很细致的给大家说明啦~
树高咋求???
🤔我们现在掌握的方法只有层次遍历来求树高,那我们怎么用递归来求树高呢???
我们现在先拿最极端情况来说明,如果一棵树没有一个元素,那我们的树高是不是为0,这样来看,我们的终止条件就找到啦!,没错就是当根节点为空的是后,我们就返回0;
我们的树高应该看最长的一部分,那我们就应该先定义两个高度,一个是左子树高度,另一个是右子树高度,之后我们比较左子树高度和右子树高度哪个高,哪个高哪个就决定了树高,因为左子树和右子树都是从第二层开始才有的,所以我们最后返回的树高应该让左右子树+1。
这样来看我们大概的逻辑不就出来了嘛?
先写一个极端判断条件,然后比较左右子树高度即可。
int treeheight(treenode* root)
{if(root==NULL)return 0;int lh=treeheight(root->lchild);int rh=treeheight(root->rchild);return lh>rh?lh+1:rh+1;
}这样看来是不是还挺简单嘞,嘿嘿。
那我们接着来下面的知识,如何查找元素嘞?
怎么查找树里面的元素???
查找的话,我们大概想一下就知道要用bool函数来判断啦,在这个结构中,我们首先要把根节点和查找的元素定义起来。
我们怎么查找呢?肯定也是一层一层查找,如果一棵树都查完了也没找的这个元素,那我们就可以说这棵树没有这个元素。
由此我们可以得到我们判断结束的条件,当树不为空时候,我们就循环;如果为空,我们就结束判断。
代码部分也是很简单,如下:
bool find(treenode* root,int target)
{while(root){if(root->value==target)return 1;if(root->value<target)root=root->lchild;if(root->value>target)root=root->rchild;}
}由以上内容,和之前的文章,我们现在掌握了如何构建查找二叉树,如何前中后序遍历,如何层次遍历,如何求树高,如何查找元素,二叉树中基本的知识,我们大概已经学完啦,下面我们来认识一个重要的树,哈夫曼树。
哈夫曼树
定义:
我们首先了解哈夫曼树的定义:
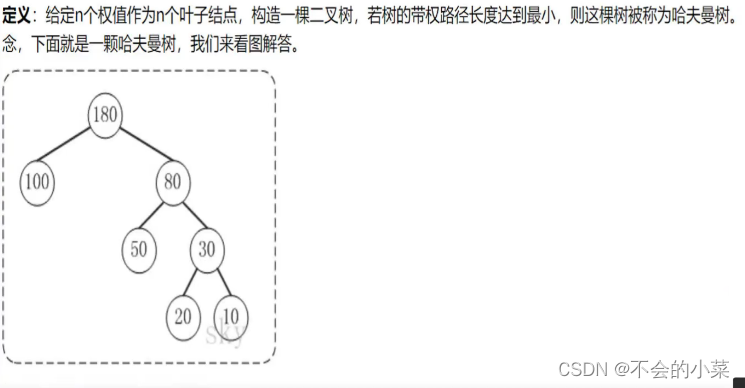
对于哈夫曼树,我们的权值只有叶子结点!!



性质:
1.权值越大的叶子节点越靠近根节点
2.权值越小的叶子节点越远离根节点
3.哈夫曼树并不唯一
4.哈夫曼树的子树也是哈夫曼树
5.哈夫曼树无度为1的结点
这些性质也是比较好看出来的,在这里就不多余赘述啦~
哈夫曼树的构建:
结点的不同:
在我们构建搜索二叉树时候,我们初始将左右子树设置为空,但是在我们的哈夫曼树的初始化时,我们应该将左右子树保留。
如下:
struct treenode{int weight;treenode* lchild;treenode* rchild;treenode(int v,treenode* l,treenode* r){weight=v,lchild=l,rchild=r;}
};因为我们左右孩子会构造出来我们的根节点,所以左右孩子这里不为空。
构建过程:
1.我们首先要把每个节点初始化,之后push进我们的vector里面
2.定义左孩子,右孩子,根节点三个变量
3.对元素进行降序排列,之后再弹出最后两个元素,同时利用最后两个元素构建出我们的父节点。
(此时的父节点需要new来开辟空间)。
过程也相对容易,接下来是代码部分:
void build(vector<int> a){vector<treenode*>b;for(int i=0;i<a.size();i++){treenode* tmp=new treenode(a[i],NULL,NULL);b.push_back(tmp);}treenode* l=NULL,*r=NULL,*p=NULL;while(b.size()>1){sort(b.begin(),b.end(),[=](treenode* a,treendoe* b){return a->weight>b.weight;});l=b[b.size()-1];b.pop_back();r=b[b.size()-1];b.pop_back();p=new treenode(l->weight+r->weight,l,r);}return p;
}求WPL
怎么求wpl呢?这里就用到了我们之前学的层次遍历啦。
我们首先层次遍历,判断结点是否没有左右孩子,这样就能找到我们的叶子节点,然后乘以我们的层次-1,如此加和进去就可以得到我们的wpl啦
void layersearch(treenode* root)
{queue<treenode*>q;q.push(root);treenode* last=root;treenode* nlast=NULL;while(!q.empty()){treenode* tmp=q.front();cout<<tmp->weight;if(tmp->lchild==NULL&&tmp->rchild==NULL){wpl+=tmp->weight*L;}q.pop();if(tmp->lchild==NULL){q.push(tmp->lchild);nlast=tmp->lchild;}if(tmp->rchild==NULL){q.push(tmp->rchild);nlast=tmp->rchild;}if(tmp==last){cout<<endl;L++;last=nlast;}}}//以上就是我们树里面残留的问题啦,一些基本的原理和代码部分我都有提到,在这里还得看大家自己下去的实践能力,多打代码,才能更透彻的了解,理解底层逻辑。
如果我的文章对对大家有帮助的作用,希望大家多多支持哦~~(谢谢大家的点赞关注啦~)
阿里嘎多everybody~
相关文章:

挑战30天C++基本入门(DAY8--树)[part 3](速通哦~)
#上一章我们把搜索二叉树的知识给传授完毕,如果认真的看下去并且手打了几遍,基本上内部的逻辑还是可以理解的,那我们现在就截至继续学习树的一些重要知识啦~~ 树高怎么求呀?如果用上一次学的层次遍历来求树高,有点小题…...
在虚拟机尝试一次用启动盘重装系统
在虚拟机尝试一次用启动盘重装系统 没有自己重装过系统,也不敢对自己的笔记本下手,用虚拟机重装玩玩试试。 先设置成u盘启动 从boot中选择相应的创建的硬盘即可(刚刚突然发现图片不能上传了,经过乱七八糟的尝试后,开一…...
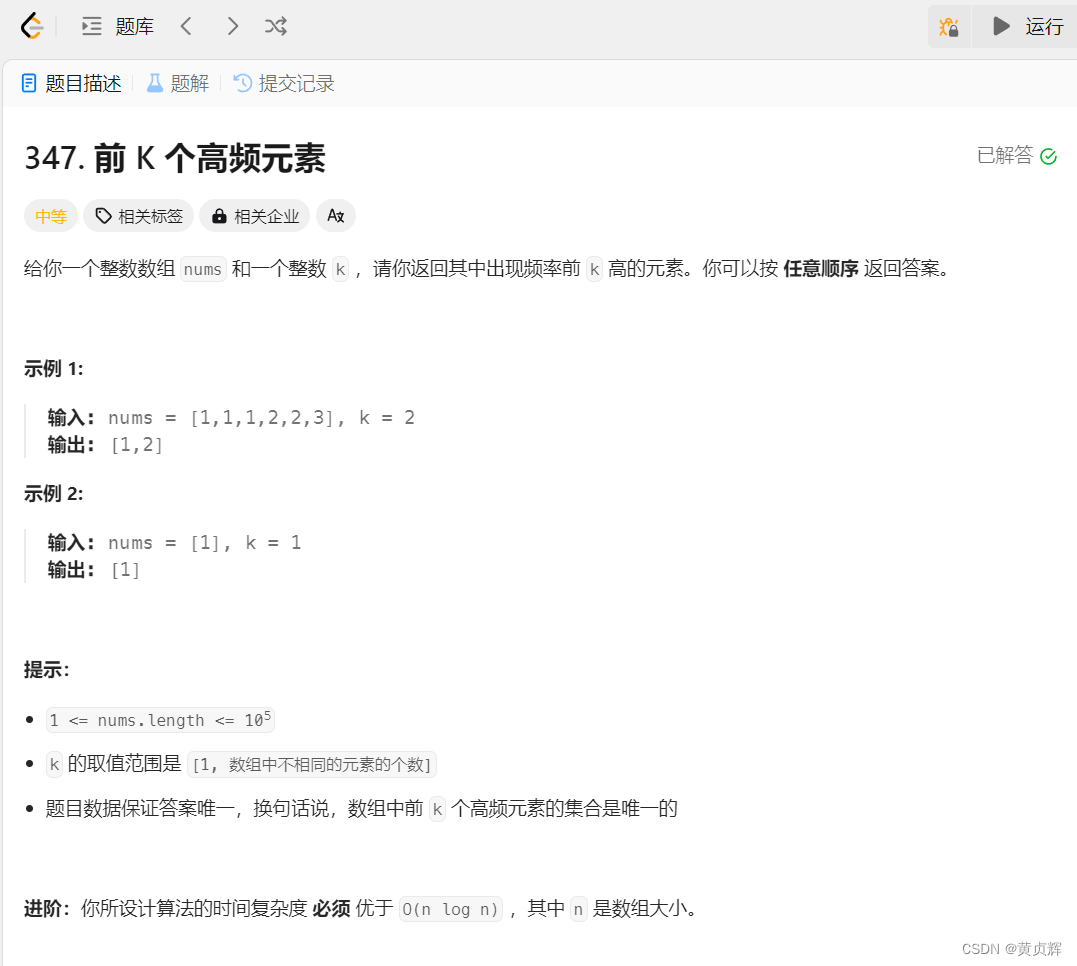
力扣347. 前 K 个高频元素
思路:记录元素出现的次数用map; 要维护前k个元素,不至于把所有元素都排序再取前k个,而是新建一个堆,用小根堆存放前k个最大的数。 为什么是小根堆?因为堆每次出数据时只出堆顶,每次把当前最小的…...
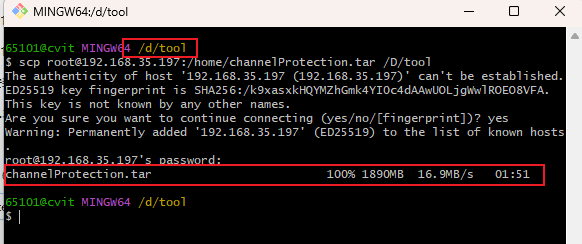
SCP 从Linux快速下载文件到Windows本地
需求:通过mobaxterm将大文件拖动到windows本地速度太慢。 环境:本地是Windows,安装了Git。 操作:进入文件夹内,鼠标右键,点击Git Bash here,然后输入命令即可。这样的话,其实自己本…...
plasmo内容UI组件层级过高导致页面展示错乱
我使用plasmo写了一个行内样式的UI组件,但是放到页面上之后,会和下拉组件出现层级错乱,看了一下样式,吓我一跳:层级竟然设置的如此之高 所以就需要将层级设置低一点: #plasmo-shadow-container {z-index: …...
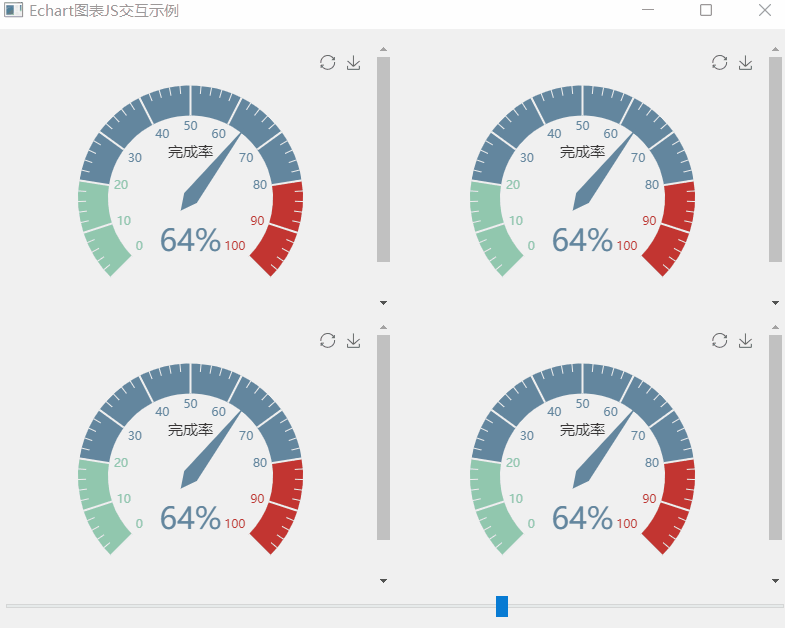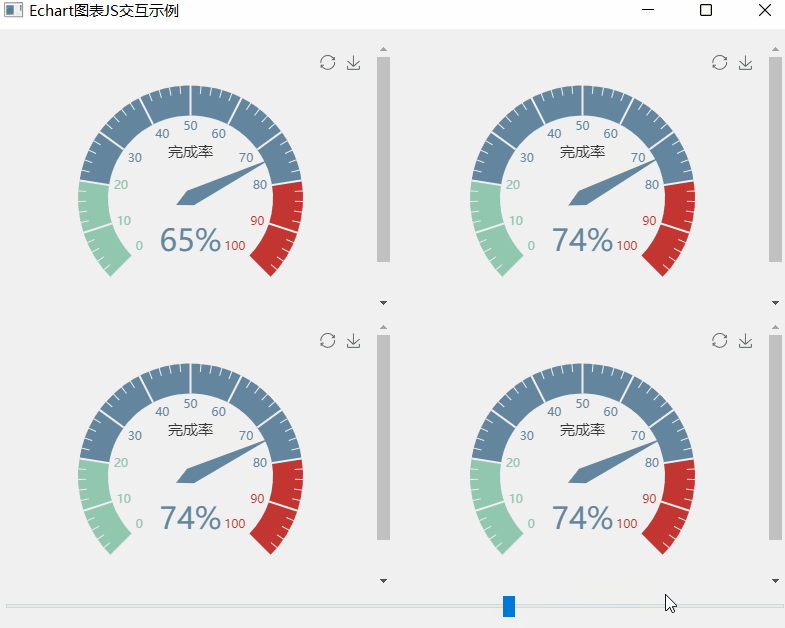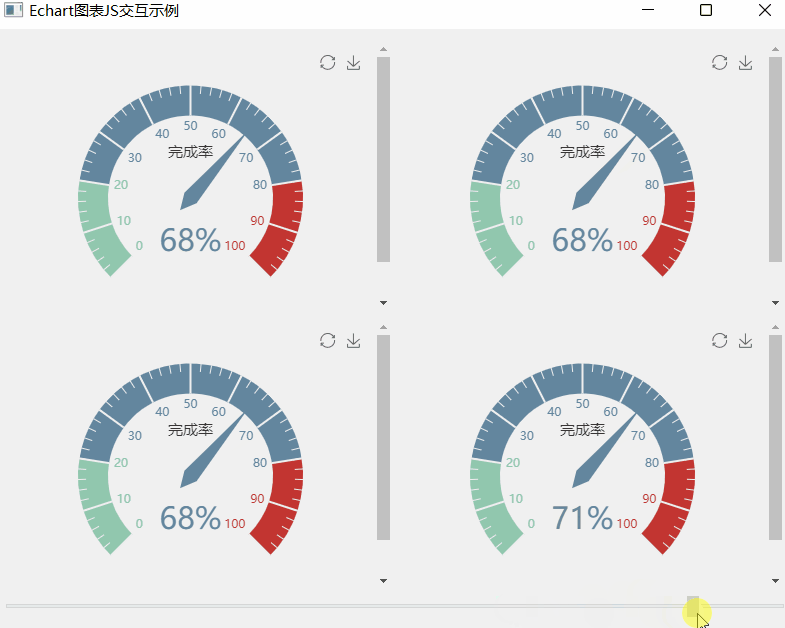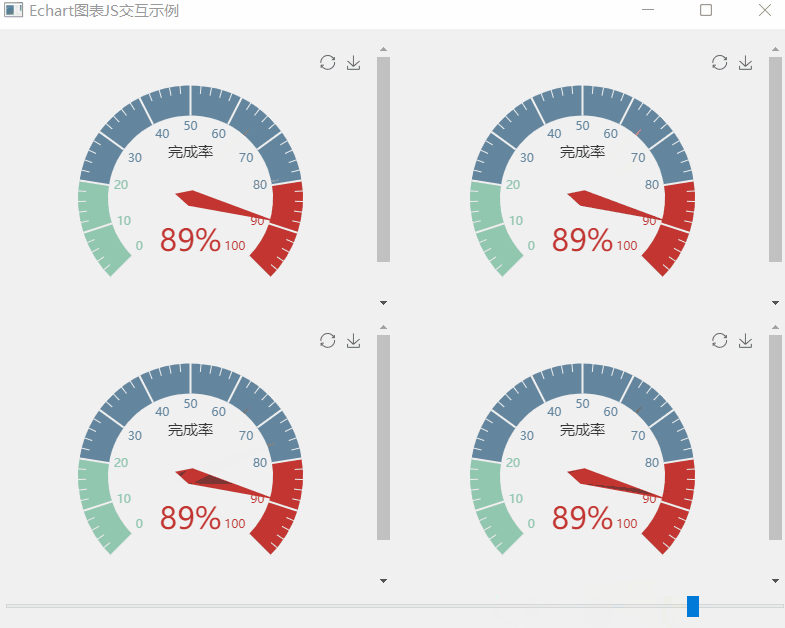
《QT实用小工具·十一》Echart图表JS交互之仪表盘
1、概述 源码放在文章末尾 该项目为Echart图表JS交互之炫酷的仪表盘,可以用鼠标实时改变仪表盘的读数。 下面为demo演示: 该项目部分代码如下: #include "widget.h" #include "ui_widget.h" #include "qurl.h&q…...

深入浅出理解ArrayBuffer对象TypedArray和DataView视图
目录 举例理解 1. ArrayBuffer对象 2. TypedArray 3. DataView 总结 具体讲解 1. ArrayBuffer对象 2. TypedArray 3. DataView 注意事项 举例理解 先举个简单的例子理解ArrayBuffer对象TypedArray和DataView视图的概念和之间的关系 1. ArrayBuffer对象 想象一个场景…...

人工智能 - 服务于谁?
人工智能服务于谁? 人工智能服务于生存,其最终就是服务于战争(热战、技术战、经济战) 反正就是为了活着而战的决策。 既然人工智能所有结果,来自大数据的分挖掘(分析)也就是数据的应用&#x…...

软考高级架构师:嵌入式系统的内核架构
作者:明明如月学长, CSDN 博客专家,大厂高级 Java 工程师,《性能优化方法论》作者、《解锁大厂思维:剖析《阿里巴巴Java开发手册》》、《再学经典:《Effective Java》独家解析》专栏作者。 热门文章推荐&am…...

分布式锁实战
4、分布式锁 4.1 、基本原理和实现方式对比 分布式锁:满足分布式系统或集群模式下多进程可见并且互斥的锁。 分布式锁的核心思想就是让大家都使用同一把锁,只要大家使用的是同一把锁,那么我们就能锁住线程,不让线程进行&#x…...

【VMware Workstation】启动虚拟机报错“此主机支持 AMD-V,但 AMD-V 处于禁用状态”
问题出现步骤: 打开虚拟机: 然后报错: “此主机支持 AMD-V,但 AMD-V 处于禁用状态。 如果已在 BIOS/固件设置中禁用 AMD-V,或主机自更改此设置后从未重新启动,则 AMD-V 可能被禁用。 (1) 确认 BIOS/固件设…...
非关系型数据库(缓存数据库)redis的基础认知与安装
目录 一.关系型数据库和非关系型数据库 关系型数据库 非关系型数据库 关系数据库与非关系型数据库的区别 ①非关系数据 关系型数据库 非关系型数据库产生背景 数据存储流向 非关系型数据库 关系数据库 二.redis的简介 1.概念 2.Redis 具有以下几个优点: 3.Redi…...

Go语言如何处理文件
1.文件的重要性 文件不过是硬盘中的数据,看起来好像没什么了不起,但实际上,文件能够让程序员管理配置、存储程序的状态乃至从底层操作系统中读取数据。 UNIX型操作系统的一个重要特征是,将一切都视为文件。这意味着在操作系统看来,从键盘到打印机的所有东西都可像文件那样…...
)
Java基础知识总结(42)
(1)Java关键字的相关知识进行了复习 考试过程中“main”是主方法名,而不是Java关键字 (2)类型转换 当一个算术表达式中包含多个基本类型的值时,整个算术表达式的数据类型将发生自动提升,所有的b…...

C++ | Leetcode C++题解之第6题Z字形变换
题目: 题解: class Solution { public:string convert(string s, int numRows) {int n s.length(), r numRows;if (r 1 || r > n) {return s;}string ans;int t r * 2 - 2;for (int i 0; i < r; i) { // 枚举矩阵的行for (int j 0; j i &l…...
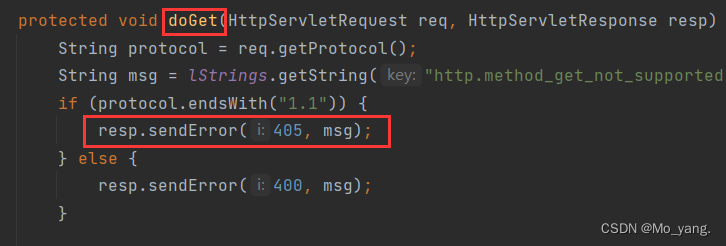
JavaEE——手把手教你实现简单的 servlet 项目
文章目录 一、什么是 Servlet二、创建一个简单的 Servlet 程序1. 创建项目2.引入依赖3. 创建目录4.编写代码5. 打包程序6. 部署7.验证整体过程总结 三、使用 Smart Tomcat 插件简化项目创建四、创建项目时可能遇到的几个问题。 一、什么是 Servlet Servlet 是一种实现 动态页面…...

X年后,ChatGPT会替代底层程序员吗?
能不能替代,真的很难说,因为机器换掉人,这其实是一个伦理问题。 其实说白了,任何行业在未来都会被AI或多或少的冲击到,因为ChatGPT做为一个可以持续提升智能的AI,在某些方面的智能程度超过人类并不是什么难…...

OpenAI 推出新网络爬虫GPTBot,为GPT-5做准备
目录 一、GPTBot是什么?它是如何工作的?二、GPTBot 与 Google Bot 等搜索引擎网络爬虫有何不同?三、GPTBot 与 Perplexity AI 的网络爬虫有何不同?四、允许 GPTBot 爬取有哪些风险和好处?4.1 允许 GPTBot 的好处4.2 允…...

【Easy云盘 | 第二篇】后端统一设计思想
文章目录 4.1后端统一设计思想4.1.1后端统一返回格式对象4.1.2后端统一响应状态码4.1.3后端统一异常处理类4.1.4StringUtils类4.1.5 RedisUtils类 4.1后端统一设计思想 4.1.1后端统一返回格式对象 com.easypan.entity.vo.ResponseVO Data public class ResponseVO<T> …...
,面试题)
c语言:模拟字符串拷贝功能(strcpy),面试题
面试题:优化中的优化(10分满分) 字符串拷贝:是将一个字符串的内容复制到另一个字符串中的操作。 运用函数模拟字符串拷贝:(5分) 模拟字符串拷贝 #include <stdio.h> void my_strcpy(char* dest, c…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
