JavaSe第6次笔记
1.不建议使用c语言的数组的表示方法。
2.二维数组表示方法

3.数组整体初始化时,只能在定义时初始化。
int[] array;
array = new int[]{1, 2};
4. boolean类型数组,默认值是false,String类型数组,默认是null,其它是0(不是随机值)。
5. array.length直接拿到数组的长度。
6.打印数组的第二种方法
for(int x : array) {
sout(x);
}
7.打印数组的第三种方法:
sout(Arrays. toString(array));
和Scanner一样,需要导包。
8.数组是引用类型,数组内存在堆区。
array是局部变量,存在栈区。
array这个引用指向对象。
9. java内存分为a.方法区,b.虚拟机栈,c.本地方法栈,d.堆,e.程序计数器。
底层方法使用c/ c++来实现(jvm)。
相关文章:

JavaSe第6次笔记
1.不建议使用c语言的数组的表示方法。 2.二维数组表示方法 3.数组整体初始化时,只能在定义时初始化。 int[] array; array new int[]{1, 2}; 4. boolean类型数组,默认值是false,String类型数组,默认是null,其它是…...

单例设计模式
介绍 单例模式是一种创建型设计模式,其主要特点包括: 只有一个实例:单例模式确保系统中只有一个实例对象存在,所有对该对象的访问都是对同一个对象的引用全局访问:单例模式可以全局访问该实例对象,避免了多个对象之间的冲突和竞争延迟初始化:单例模式通常使用延迟初始化技术,…...
)
第七章 opengl之光照(基础光照)
OpenGL基础光照环境光照漫反射光照镜面光照基础光照 主要需要理解一个模型是冯氏光照模型,主要结构由3个分量组成:环境,漫反射,镜面光照。下面分别描述下这三个光照: 环境光照(Ambient Lighting):即使在黑…...
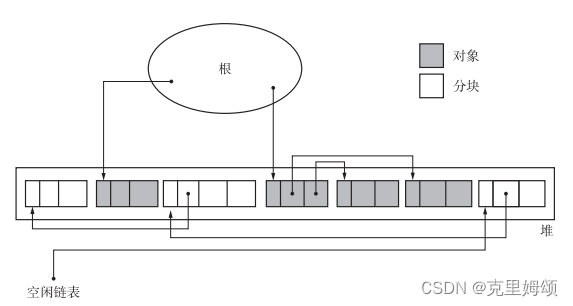
不考虑分配与合并情况下,GO实现GCMarkSweep(标记清除算法)
观前提醒 熟悉涉及到GC的最基本概念到底什么意思(《垃圾回收的算法与实现》)我用go实现(因为其他的都忘了,(╬◣д◢)ムキー!!) 源码地址(你的点赞,是我开源的…...
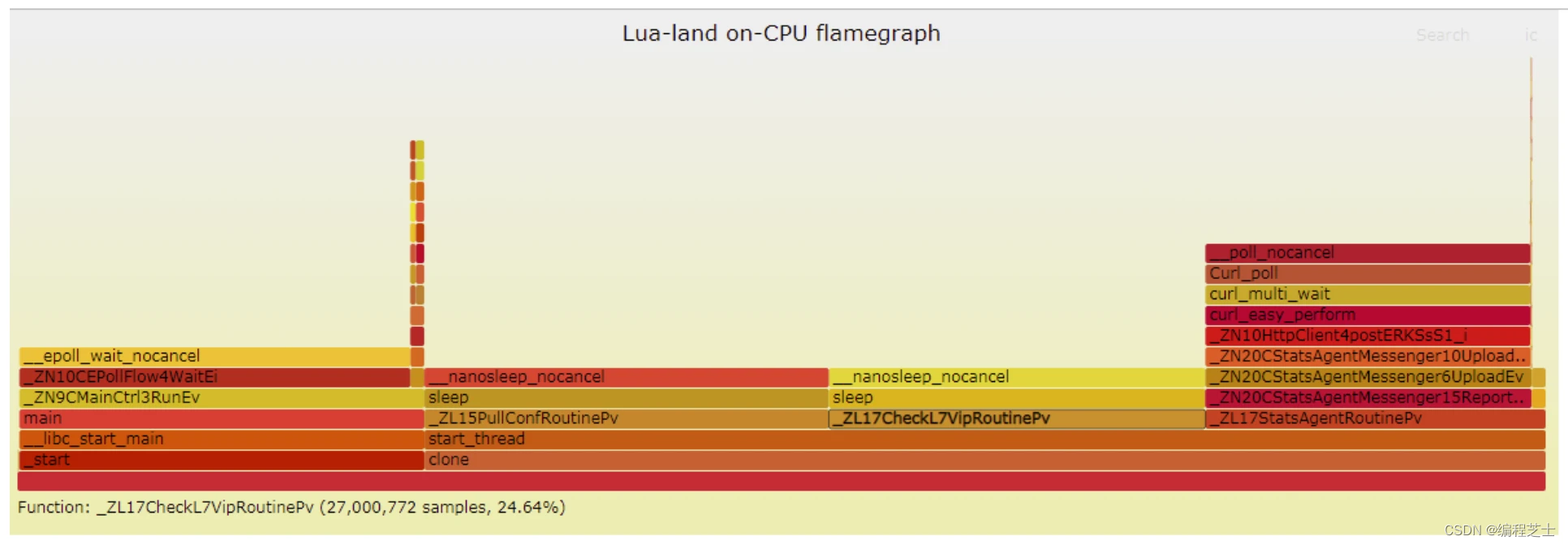
性能分析利器:火焰图
什么是火焰图 火焰图(FlameGraph)是是由 Linux 性能优化大师 Brendan Gregg 发明的。通过 perf 等工具分析得到结果,看起来就像是火焰,这也是它的名字的由来。火焰图以一个全局的视野来看待时间分布,它从底部往顶部&am…...
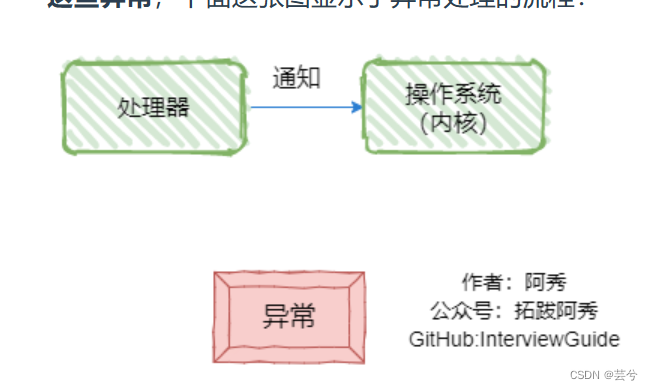
八股总结(三)操作系统内存管理、进程线程、进程同步与通信、中断与异常、常用命令
layout: post title: 八股总结(三)操作系统内存管理、进程线程、进程同步与通信、中断与异常、常用命令 description: 八股总结(三)操作系统内存管理、进程线程、进程同步与通信、中断与异常、常用命令 tag: 八股总结 文章目录操作…...
)
概率论小课堂:条件概率和贝叶斯公式(机器翻译的工作原理)
文章目录 引言I 条件概率1.1 条件概率的定义1.2 条件概率的计算II 贝叶斯公式2.1贝叶斯公式的本质2.2 机器翻译的原理引言 对于几乎所有的随机事件来讲,条件概率由于条件的存在,它通常不等于本身的概率。 贝叶斯公式的本质:在数学上条件和结果可以互换,通过这种互换,可以…...

流量与日志分析
文章目录1.流量与日志分析1.1系统日志分析1.1.1window系统日志与分析方法1.1.2linux 系统日志与分析方法1.2 web日志分析iis 日志分析方法apache日志分析**access_log****error_log**nginx日志分析tomcat 日志分析主流日志分析工具使用1.流量与日志分析 日志,是作为…...
)
英文论文写作常用例句整理汇总(持续更新)
ContentsGeneral introductionProblem definitionGaps in literatureProblems solutionStudy motivationAims & objectivesSignificance and advantages of your work参考资料General introduction Research on __ has a long tradition For decades, one of the most pop…...
[N0wayBack 练习题] My_enc,Euler,EasyLock,RRRRSA,EasyNumber,pwn
加入一个队,队里的练习题不少,还有WP真好My_enc原题from secret import flag import randomdef Cyber_key(LEN):Key [[] for i in range(row)]for x in range(row):for i in range(LEN):Key[x].append(random.randint(0, 2023))return Keydef Punk_enc(Key, msg):out []for l…...
网分线缆测试和dc-block
今天的好苹果和坏苹果 好苹果:是校准件和网分都是好的,又给了我一次复盘的机会 网分测试线缆: 1.网分直接复位,如果网分复位是校准状态,且解的是精密转接头,BNC的,可以不校准,结果差…...

Java创建线程的方式只有一种:Thread+Runnable
Java创建线程的方式其实只有一种👨🎓一、继承Thread👨🎓二、实现Runnable接口👨🎓三、实现Callable接口👨🎓四、通过线程池创建👨🎓五、总结一般我…...
)
数据加密--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例6:数据加密 数据加密是保存数据的一种方法,它通过加密算法和密钥将数据从明文转换为密文。 假设当前开发的程序中需要对用户的密码进行加密处理,已知用户的密码均为6位数字,其加密规则如下: 获取每个数字的ASCI…...
【GO】K8s 管理系统项目33[前端部分–登录和登出]
K8s 管理系统项目[前端部分–登录和登出] 1. 登录登出流程 1.1 登录流程 登入流程总的分为5步: 账号密码验证token生成token验证验证成功进行跳转验证失败返回/login 1.2 登出流程 登出流程就相对简单,分为2步 删除Token跳转/login 2. 登录代码 src/views/login/Login.v…...
Vue 计算属性基础知识 监听属性watch
计算属性的概念 在{{}}模板中放入太多的逻辑会让模板内容过重且难以维护。例如以下代码: <div id"app">{{msg.split().reverse().join()}}</div><script>const vm new Vue({el: "#app",data: {msg:我想把vue学的细一点}})&…...
)
PAT:L1-004 计算摄氏温度、L1-005 考试座位号、L1-006 连续因子(C++)
目录 L1-004 计算摄氏温度 问题描述: 实现代码: L1-005 考试座位号 问题描述: 实现代码: 原理思路: L1-006 连续因子 问题描述: 实现代码: 原理思路: 过于简单的就不再写…...

Redis集群方案应该怎么做?
今天我们来跟大家唠一唠JAVA核心技术-RedisRedis是一款流行的内存数据库,适用于高性能的数据缓存和实时数据处理。当需要处理大量数据时,可以使用Redis集群来提高性能和可用性。Redis在单节点模式下,虽然可以支持高并发、快速读写、丰富的数据…...

连续点击返回键退出Android 应用
问题 业务需要,在主界面连续点击返回键退出应用,记录一下。 解决方案 先说结论,在主界面Activity中添加如下代码 /*** 记录上次点击返回键时间*/private long lastClickTime 0;/*** 两次回退点击时间间隔设置不小于2s*/public static fi…...
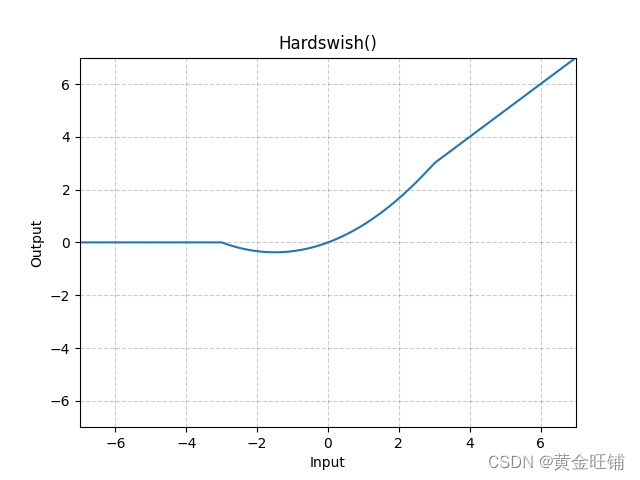
【PyTorch】教程:torch.nn.Hardswish
torch.nn.Hardswish 原型 CLASS torch.nn.Hardswish(inplaceFalse) 参数 inplace (bool) – 内部运算,默认为 False 定义 Hardswish(x){0if x≤−3,xif x≥3,x⋅(x3)/6otherwise\text{Hardswish}(x) \begin{cases} 0 & \text{if~} x \le -3, \\ x & \te…...
nacos源码入门
nacos官方文档地址:nacos官方文档 Nacos /nɑ:kəʊs/ 是 Dynamic Naming and Configuration Service的首字母简称,一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。 简单来说,nacos就是一个注册中心、配置中心࿰…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
