Python---Numpy线性代数
1.数组和矩阵操作:
创建数组和矩阵:np.array, np.matrix
基本的数组操作:形状修改、大小调整、转置等
import numpy as np# 创建一个 2x3 的数组
A = np.array([[1, 2, 3], [4, 5, 6]])
print("数组 A:\n", A)# 将数组 A 转换为矩阵
B = np.matrix(A)
print("矩阵 B:\n", B)# 例一:
# 定义两个矩阵 C 和 D
C = np.array([[1, 2], [3, 4]])
D = np.array([[5, 6], [7, 8]])# 进行矩阵乘法
result = np.dot(C, D)
print("矩阵乘法结果:\n", result)# 例二:
x1 = np.array([[1, 2, 3], [4, 5, 6]])x2 = np.array([[1, 2], [3, 4],[5, 6]])# 矩阵乘法
print(x1.dot(x2))# 计算对角线之和
print(x2.trace())
2.线性代数运算:
矩阵乘法:np.dot, np.matmul
内积和外积:np.inner, np.outer
点积:np.dot (对于一维数组)
对角线之和:np.trace()
# 定义系数矩阵和常数向量
coefficients = np.array([[3, 1], [1, 2]])
constants = np.array([9, 8])# 求解线性方程组
solution = np.linalg.solve(coefficients, constants)
print("线性方程组的解:\n", solution)3.特征值和特征向量:
计算矩阵的特征值和特征向量:np.linalg.eig
特征值分解:np.linalg.eigvalsh, np.linalg.eigh
# 定义一个需要计算特征值和特征向量的矩阵
E = np.array([[1, 2], [2, 1]])# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(E)
print("特征值:\n", eigenvalues)
print("特征向量:\n", eigenvectors)4.矩阵分解:
奇异值分解(SVD):np.linalg.svd
卢分解(LU):np.linalg.lu
特征值分解(如前所述)
# 定义一个用于奇异值分解的矩阵
F = np.array([[2, 3], [4, 5]])# 进行奇异值分解
U, S, VT = np.linalg.svd(F)
print("U 矩阵:\n", U)
print("奇异值:\n", S)
print("VT 矩阵:\n", VT)5.线性方程组求解:
解决线性方程组:np.linalg.solve
计算矩阵的逆:np.linalg.inv
# 定义一个矩阵
G = np.array([[1, 2], [3, 4]])# 计算行列式
det_G = np.linalg.det(G)
print("矩阵 G 的行列式:\n", det_G)# 计算矩阵的迹
trace_G = np.trace(G)
print("矩阵 G 的迹:\n", trace_G)
6.行列式和迹:
计算矩阵的行列式:np.linalg.det
计算矩阵的迹:np.trace
# 创建一个 3x3 矩阵
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 计算矩阵的行列式
det_value = np.linalg.det(matrix)
print("矩阵的行列式为:", det_value)
# 使用之前定义的矩阵
trace_value = np.trace(matrix)
print("矩阵的迹为:", trace_value)7.范数和条件数:
计算向量的范数:np.linalg.norm
计算矩阵的条件数:np.linalg.cond
# 定义一个向量
vector = np.array([3, 4])# 计算向量的 L2 范数
norm = np.linalg.norm(vector)
print("向量的 L2 范数:\n", norm)8.三角函数和相关函数:
正弦、余弦等三角函数:np.sin, np.cos 等
反三角函数:np.arcsin, np.arccos 等
# 定义一个包含两个元素的数组,代表角度(以弧度为单位)
angles = np.array([0, np.pi / 2])# 计算正弦和余弦值
sine_values = np.sin(angles)
cosine_values = np.cos(angles)print("角度的正弦值:", sine_values)
print("角度的余弦值:", cosine_values)# 定义一个包含两个元素的数组,代表正弦和余弦值
sine_cosine_values = np.array([np.sin(np.pi / 4), np.cos(np.pi / 4)])# 计算反正弦和反余弦值
arc_sine_value = np.arcsin(sine_cosine_values[0])
arc_cosine_value = np.arccos(sine_cosine_values[1])print("反正弦值:", arc_sine_value)
print("反余弦值:", arc_cosine_value)
相关文章:

Python---Numpy线性代数
1.数组和矩阵操作: 创建数组和矩阵:np.array, np.matrix 基本的数组操作:形状修改、大小调整、转置等 import numpy as np# 创建一个 2x3 的数组 A np.array([[1, 2, 3], [4, 5, 6]]) print("数组 A:\n", A)# 将数组 A 转换为矩阵…...

react+ echarts 轮播饼图
react echarts 轮播饼图 图片示例 代码 import * as echarts from echarts; import { useEffect } from react; import styles from ./styles.scss;const Student (props) > {const { dataList, title } props;// 过滤数据const visionList [{ value: 1048, name: Se…...
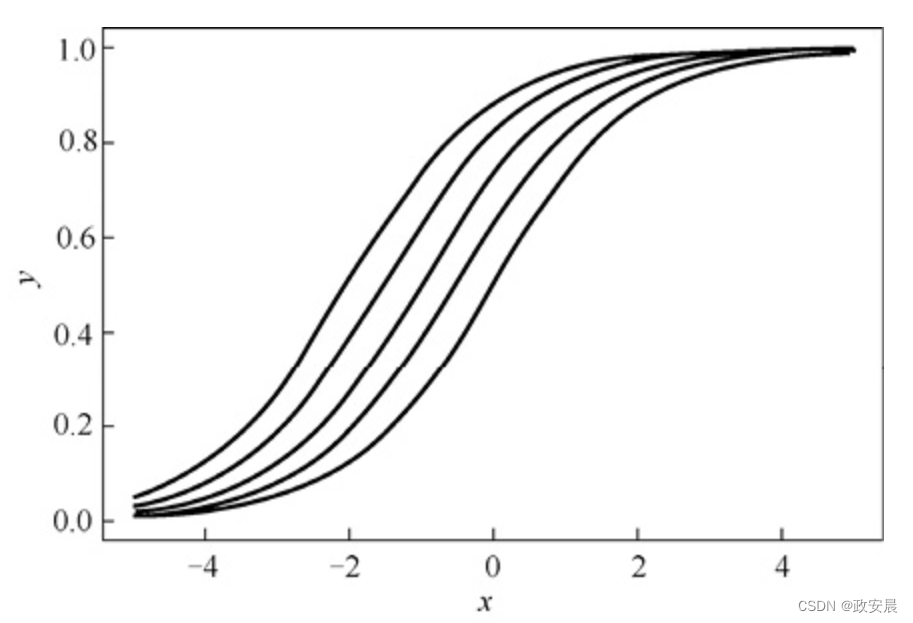
政安晨:【深度学习神经网络基础】(三)—— 激活函数
目录 线性激活函数 阶跃激活函数 S型激活函数 双曲正切激活函数 修正线性单元 Softmax激活函数 偏置扮演什么角色? 政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: 政安晨的机器学习笔记 希望政安晨的博客能够对您有所裨…...
使用tomcat里的API - servlet 写动态网页
一、创建一个新的Maven空项目 首次创建maven项目的时候,会自动从maven网站上下载一些依赖组件(这个过程需要保证网络稳定,否则后续打包一些操作会出现一些问题) ps:校园网可能会屏蔽一些网站,可能会导致maven的依赖…...
从0到1搭建文档库——sphinx + git + read the docs
sphinx git read the docs 目录 一、sphinx 1 sphinx的安装 2 本地构建文件框架 1)创建基本框架(生成index.rst ;conf.py) conf.py默认内容 index.rst默认内容 2)生成页面(Windows系统下…...

EasyExcel 校验后导入
引入pom <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.3.3</version></dependency>触发校验类 import com.baomidou.mybatisplus.extension.api.R; import lombok.experimental…...

【星计划★C语言】c语言初相识:探索编程之路
🌈个人主页:聆风吟_ 🔥系列专栏:星计划★C语言、Linux实践室 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️第一个c语言程序二. ⛳️数据类型2.1 🔔数据单位2.2 &…...

搜维尔科技:借助 ARVR 的力量缩小现代制造业的技能差距
借助ARVR的力量缩小现代制造业的技能差距 搜维尔科技:Senseglove案例-扩展机器人技术及其VR应用...
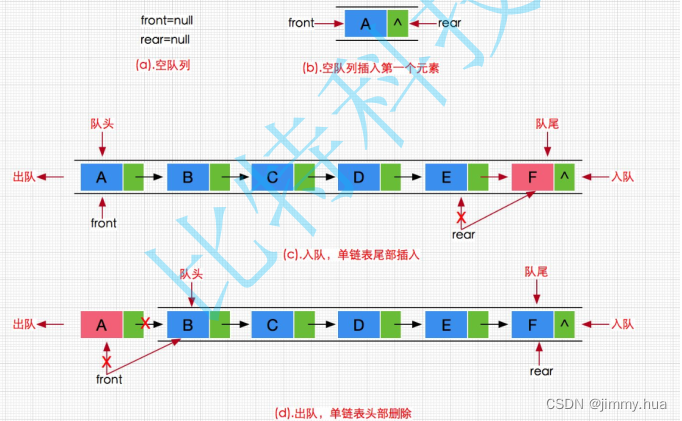
数据结构之栈和队列
1.前言 大家好久不见,这段时间由于忙去了。就没有即使维护我的博客,先给大家赔个不是。 我们还是规矩不乱,先赞后看~ 今天讲的内容是数据结构中非常重要的一个部分:栈和队列。它在今后的学习中也会再次出现(c&#…...
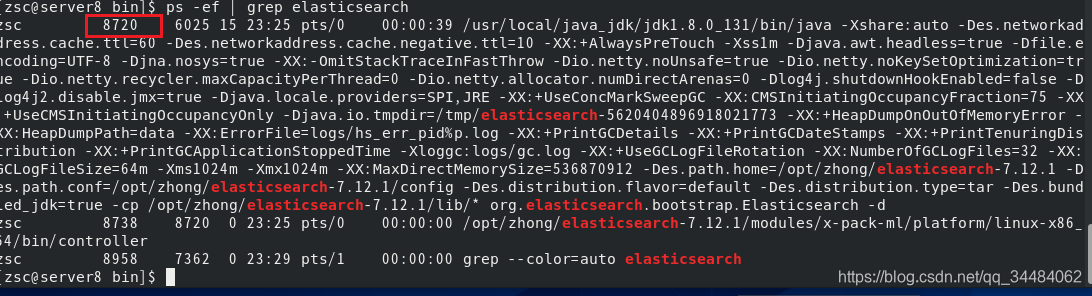
centos安装使用elasticsearch
1.首先可以在 Elasticsearch 官网 Download Elasticsearch | Elastic 下载安装包 2. 在指定的位置(我的是/opt/zhong/)解压安装包 tar -zxvf elasticsearch-7.12.1-linux-x86_64.tar.gz 3.启动es-这种方式启动会将日志全部打印在当前页面,一旦使用 ctrlc退出就会导…...
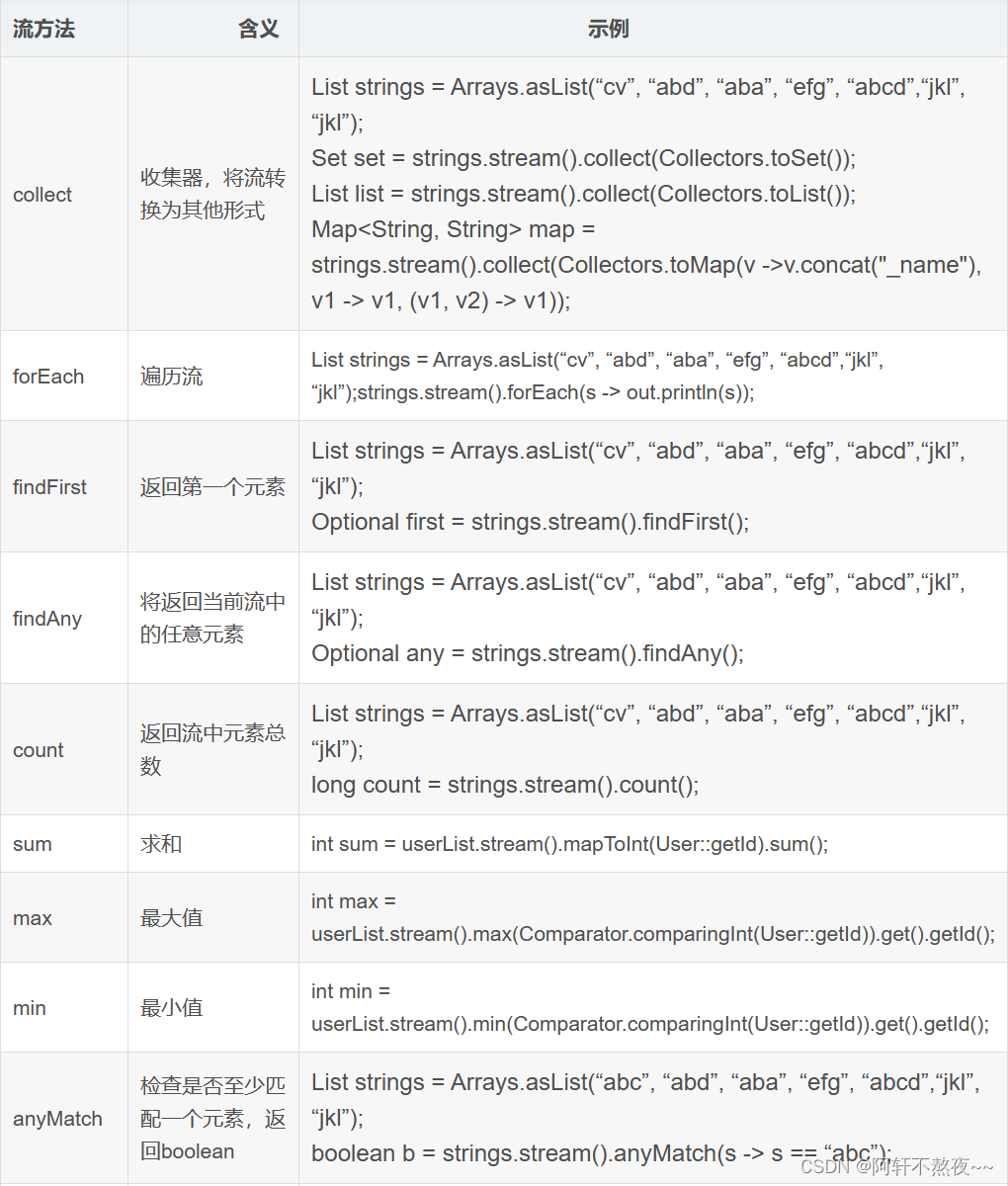
4.7学习总结
java学习 一.Stream流 (一.)概念: Stream将要处理的元素集合看作一种流,在流的过程中,借助Stream API对流中的元素进行操作,比如:筛选、排序、聚合等。Stream流是对集合(Collection)对象功能的增强&…...
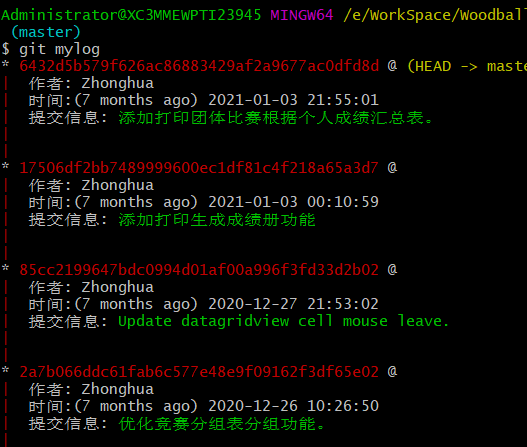
自定义gitlog格式
git log命令非常强大而好用,在复杂系统的版本管理中扮演着重要的角色,但默认的git log命令显示出的东西实在太丑,不好好打扮一下根本没法见人,打扮好了用alias命令拍个照片,就正式出道了! 在使用git查看lo…...

Redission--分布式锁
Redission的锁的好处 Redission分布式锁的底层是setnx和lua脚本(保证原子性) 1.是可重入锁。 2.Redisson 锁支持自动续期功能,这可以帮助我们合理控制分布式锁的有效时长,当业务逻辑执行时间超出了锁的过期时间,锁会自动续期,避免…...

非关系型数据库(缓存数据库)redis的集群
目录 一.群集模式——Cluster 1.原理 2.作用 3.特点 4.工作机制 哈希槽 哈希槽的分配 哈希槽可按照集群主机数平均分配(默认分配) 根据主机的性能以及功能自定义分配 redis集群的分片 分片 如何找到给定key的分片 优势 二. 搭建Redis群集…...
)
MySQL:表的约束(上)
文章目录 空属性默认值列描述zerofill主键 本篇总结的是MySQL中关于表的约束部分的内容 空属性 在进行表的创建时,会有两个值,null和not null,而数据库默认的字段基本都是空,但是在实际的开发过程中要保证字段不能为空ÿ…...
树莓派5使用体验
原文地址:树莓派5使用体验 - Pleasure的博客 下面是正文内容: 前言 好久没有关于教程方面的博文了,由于最近打算入门嵌入式系统,所以就去购入了树莓派5开发板 树莓派5是2023年10月23日正式发售的,过去的时间不算太远吧…...

代码随想录算法训练营第42天| 背包问题、416. 分割等和子集
01 背包 题目描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 二维dp数组01背包: 确定dp数组以及下标的含义 …...

Node.js安装及环境配置指南
Node.js安装及环境配置指南 一、Node.js的安装 安装Node.js之前,首先需要确保你的电脑已经安装了合适的编译器和开发环境。Node.js是一个开源的、跨平台的JavaScript运行环境,它使得JavaScript可以在服务器端运行。 下载Node.js安装包 访问Node.js的…...
【Java基础】面试题汇总
Java基础面试题1. JVM vs JDK vs JRE 2. 什么是字节码?采用字节码的好处是什么?3. 为什么说 Java 语言“编译与解释并存”?4. AOT 有什么优点?为什么不全部使用 AOT 呢?5. Java 和 C 的区别?6. Java 中的基本数据类型࿱…...
)
数据库事务的超级详细讲解,包括事务特性、事务隔离级别、MVCC(多版本并发控制)
数据库事务: 主要有事务特性,事务的隔离级别,MVCC。 事务特性: 事务(Transaction)是指作为单个逻辑工作单元执行的一系列操作,这些操作要么全部成功执行,要么全部不执行ÿ…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
