代码随想录算法训练营第42天| 背包问题、416. 分割等和子集
01 背包
题目描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
二维dp数组01背包:
- 确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。

-
确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。那么可以有两个方向推出来dp[i][j],- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
-
初始化
dp[i][j]是由其左侧和左上方数据推导出来的,因此要初始化dp[i][0]列和dp[0][j]行的数据,背包重量为0时,背包内物品的价值为零,dp[i][0]列为0。dp[0][i]行的数据,当背包容量j≥wieght[j]时,dp[0][j]=value[j],其他时候为零。 -
遍历顺序
先遍历还是weight还是value都可以。
#include<iostream>
#include<vector>
using namespace std;void slove(int m, int n){vector<int> wight;vector<int> value;int x;for (int i = 0; i < m;i++){cin>>x;wight.push_back(x);}for (int i = 0; i < m;i++){cin>>x;value.push_back(x);}vector<vector<int>> dp(m,vector<int>(n+1,0));for(int j = 0; j <= n; j++){if(j>=wight[0]){dp[0][j] = value[0];}}for (int i = 1; i < m; i++){for (int j = 1; j <= n; j++){if(j < wight[i]){dp[i][j] = dp[i-1][j];} else {dp[i][j] = max(dp[i-1][j], dp[i-1][j-wight[i]]+value[i]);}}}cout << dp[m-1][n] <<endl;
}int main(){int m,n;cin>>m>>n;slove(m,n);
}
一维dp数组01背包:
对于背包问题其实状态都是可以压缩的。
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
但是这里要注意,dp数组的遍历要为倒序遍历,倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
#include<iostream>
#include<vector>
using namespace std;void slove(int m, int n){vector<int> wight;vector<int> value;int x;for (int i = 0; i < m;i++){cin>>x;wight.push_back(x);}for (int i = 0; i < m;i++){cin>>x;value.push_back(x);}vector<int> dp(n+1,0);for (int i = 0; i < m; i++){for (int j = n; j >= 0; j--){if(j >= wight[i]){dp[j] = max(dp[j], dp[j-wight[i]]+value[i]);}}}cout << dp[n] <<endl;
}int main(){int m,n;cin>>m>>n;slove(m,n);
}
416. 分割等和子集
题目链接:分割等和子集
题目描述:给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
解题思想:
要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
后面的解题思路就和01背包问题相同
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;int target = 0;for (int num : nums)sum += num;if (sum % 2)return false;elsetarget = sum / 2;vector<int> dp(target + 1, 0);for (int i = 0; i < nums.size(); i++) {for (int j = target; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}if (dp[target] == target) {return true;}return false;}
};
相关文章:

代码随想录算法训练营第42天| 背包问题、416. 分割等和子集
01 背包 题目描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 二维dp数组01背包: 确定dp数组以及下标的含义 …...

Node.js安装及环境配置指南
Node.js安装及环境配置指南 一、Node.js的安装 安装Node.js之前,首先需要确保你的电脑已经安装了合适的编译器和开发环境。Node.js是一个开源的、跨平台的JavaScript运行环境,它使得JavaScript可以在服务器端运行。 下载Node.js安装包 访问Node.js的…...
【Java基础】面试题汇总
Java基础面试题1. JVM vs JDK vs JRE 2. 什么是字节码?采用字节码的好处是什么?3. 为什么说 Java 语言“编译与解释并存”?4. AOT 有什么优点?为什么不全部使用 AOT 呢?5. Java 和 C 的区别?6. Java 中的基本数据类型࿱…...
)
数据库事务的超级详细讲解,包括事务特性、事务隔离级别、MVCC(多版本并发控制)
数据库事务: 主要有事务特性,事务的隔离级别,MVCC。 事务特性: 事务(Transaction)是指作为单个逻辑工作单元执行的一系列操作,这些操作要么全部成功执行,要么全部不执行ÿ…...

鸿蒙Lottie动画-实现控制动画的播放、暂停、倍速播放、播放顺序
介绍 本示例展示了lottie对动画的操作功能。引入Lottie模块,实现控制动画的播放、暂停、倍速播放、播放顺序、播放到指定帧停止或从指定帧开始播放、侦听事件等功能,动画资源路径必须是json格式。 效果预览 使用说明: 进入页面默认开始201…...

C++面试100问与自动驾驶100问
C的学习和面试其实是非常的不友好的,首先C的学习内容非常的多,其次C的面试不单单面试C的知识点,还有它的“七大姑八大姨”(计算机网络、数据结构、算法、计算机组成原理、操作系统、编译、xxx的底层实现 and so on)。 …...

加速 Redis 操作:掌握管道技术提升性能与效率
Redis 管道技术是一种用于优化 Redis 命令执行效率的机制。在传统的 Redis 操作中,每次向 Redis 服务器发送一个命令,都需要等待命令执行完成并返回结果,这样会导致频繁的网络通信和服务器端的命令执行开销,降低系统的性能和吞吐量…...

深入浅出 -- 系统架构之分布式系统底层的一致性
在分布式领域里,一致性成为了炙手可热的名词,缓存、数据库、消息中间件、文件系统、业务系统……,各类分布式场景中都有它的身影,因此,想要更好的理解分布式系统,必须要理解“一致性”这个概念。 其实关于…...
idea Springboot 电影推荐系统LayUI框架开发协同过滤算法web结构java编程计算机网页
一、源码特点 springboot 电影推荐系统是一套完善的完整信息系统,结合mvc框架和LayUI框架完成本系统springboot dao bean 采用协同过滤算法进行推荐 ,对理解JSP java编程开发语言有帮助系统采用springboot框架(MVC模式开发)&…...

xss【2】
1.xss钓鱼 钓鱼攻击利用页面,fish.php黑客钓鱼获取到账号密码存储的位置 xss进行键盘记录 2.xss常规防范 3.xss验证payload XSS(跨站攻击)_details/open/ontoggle-CSDN博客...

时序分解 | Matlab实现GSWOA-VMD改进鲸鱼优化算法优化变分模态分解时间序列信号分解
时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解 目录 时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解效果一览基本介绍程序设计参考资料 效果一览 基本介绍 Matlab实现GSWOA-VMD改进鲸鱼优化算法优化变分模态分解时间序…...

css- 4
1.浮动 1. 浮动最初用于实现文字环绕效果 2. 现在,浮动是主流的布局方式之一 1.1元素浮动之后的特点 元素浮动之后,称为浮动元素,具有如下特点: 1. 浮动元素脱离文档流 2. 多个浮动的元素会水平排列,一行放不下自动换…...

22.括号生成
题目描述 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”] 示例 2: 输入…...

JAVA八股--redis
JAVA八股--redis 如何保证Redis和数据库数据一致性redisson实现的分布式锁的主从一致性Redis脑裂现象及解决方案介绍I/O多路复用模型undo log 和 redo log(没掌握MyISAM 和 InnoDB 有什么区别? 如何保证Redis和数据库数据一致性 关于异步通知中消息队列…...
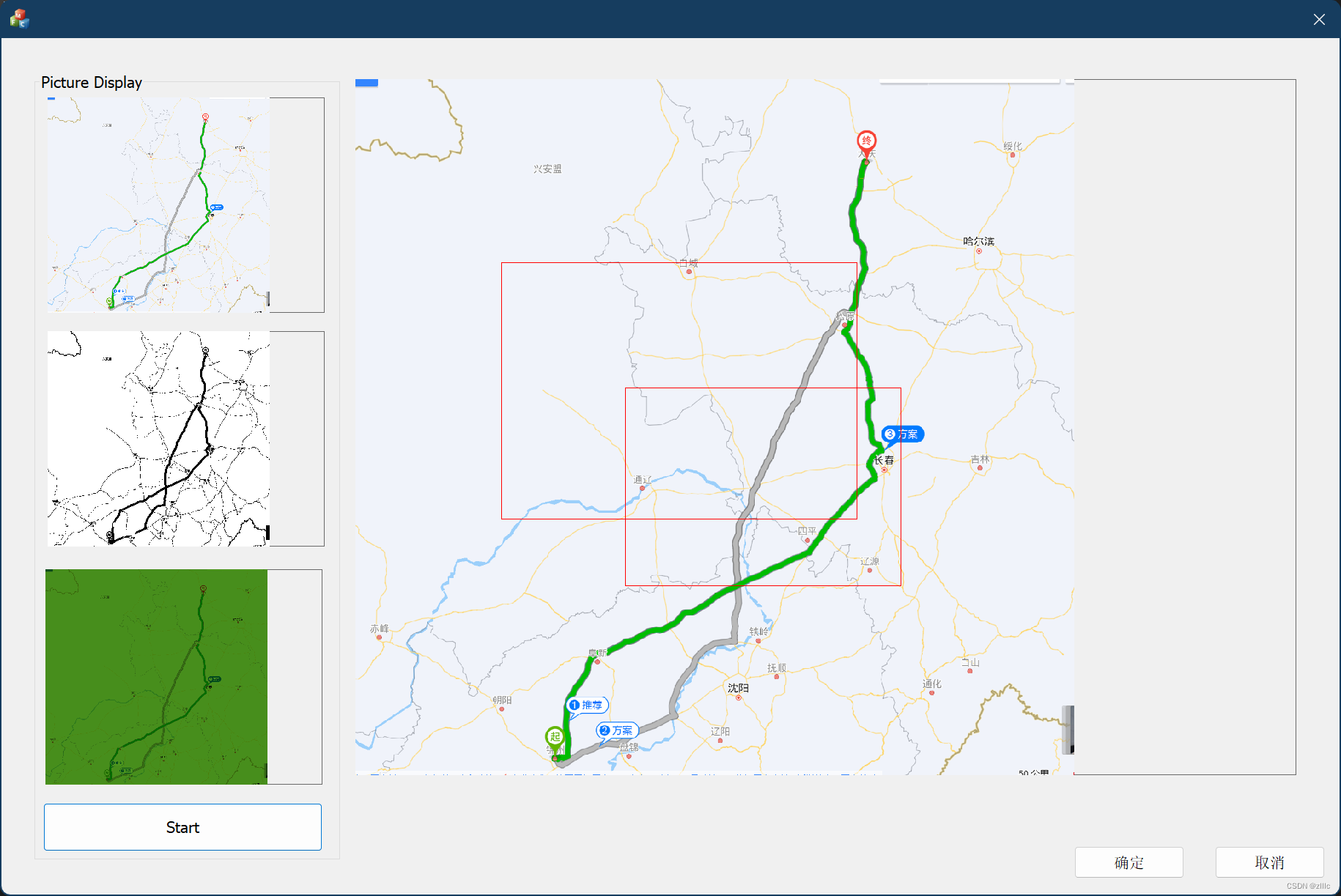
[图像处理] MFC载入图片并绘制ROI矩形
上一篇: [图像处理] MFC载入图片并进行二值化处理和灰度处理及其效果显示 文章目录 前言完整代码重要代码效果 前言 上一篇实现了MFC通过Picture控件载入图片。 这一篇实现ROI功能的第一部分,在Picture控件中,通过鼠标拖拽画出一个矩形。 完…...

Godot 4 教程《勇者传说》依赖注入 学习笔记(0):环境配置
文章目录 前言相关地址环境配置初始化环境配置文件夹结构代码结构代码运行 资源文件导入像素风格窗口环境设置背景设置,Tileap使用自动TileMap 人物场景动画节点添加站立节点添加移动动画添加 通过依赖注入获取Godot的全局属性项目声明 当前项目逻辑讲解角色下降添加代码位置问…...

强行让Java和Go对比一波[持续更新]
概述 很多Java开发如果想转Golang的话,比较让Java开发蛋疼的第一是语法,第二是一些思想和设计哲学的Gap,所以我这儿强行整理一波Java和Golang的对比,但是由于GO和Java在很多方面都有不同的设计,所以这些对比的项可以更…...

理解七层网络协议
osi体系结构 上三路(管数据) 应用层 通过http等,把传输的格式,数据打包 处理网络应用。直接为端用户服务,提供各类应用过程的接口和用户接口。例如:HTTP、Tenlent、FTP、SMTP、NFS等。基于TCP的FTP、HTTP…...
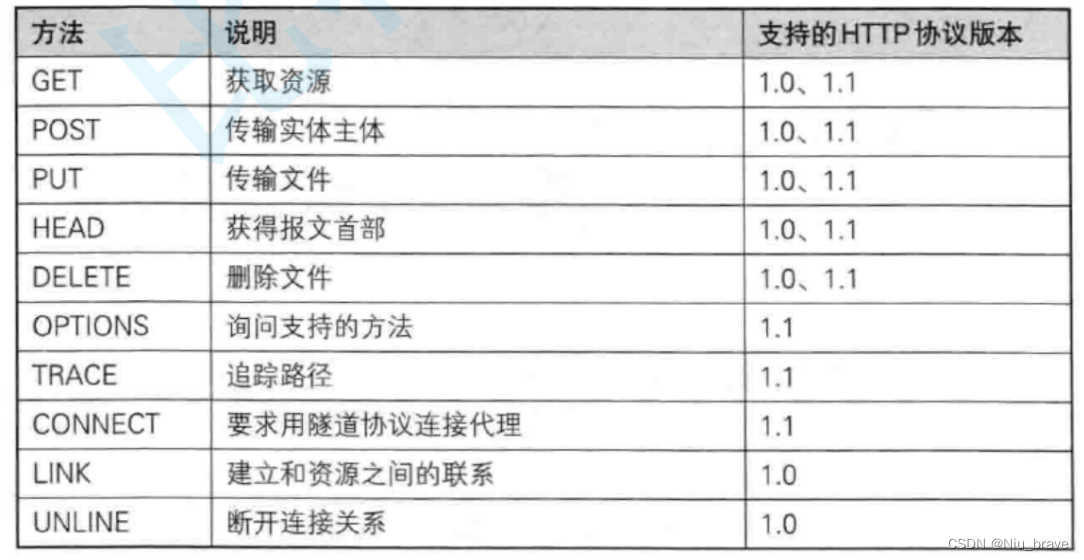
网络协议——HTTP协议
目录 编辑 一,HTTP协议基本认识 二,认识URL 三,http协议的格式 1,发送格式 2,回应格式 四,服务端代码 五,http报文细节 1,Post与Get方法 2,Content_lenth 3&…...

八股面试——数据库——索引
索引的概念 B树的概念: 索引的作用 聚簇索引与非聚簇索引 聚簇索引就是主键值,在B树上,通过主键大小(数据在B树叶子节点按主键顺序排序)寻找对应的叶子节点,叶子节点保存的一整条记录。 非聚簇索引&#x…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...
