代码+视频,手动绘制logistic回归预测模型校准曲线(Calibration curve)(2)
校准曲线图表示的是预测值和实际值的差距,作为预测模型的重要部分,目前很多函数能绘制校准曲线。
一般分为两种,一种是通过Hosmer-Lemeshow检验,把P值分为10等分,求出每等分的预测值和实际值的差距
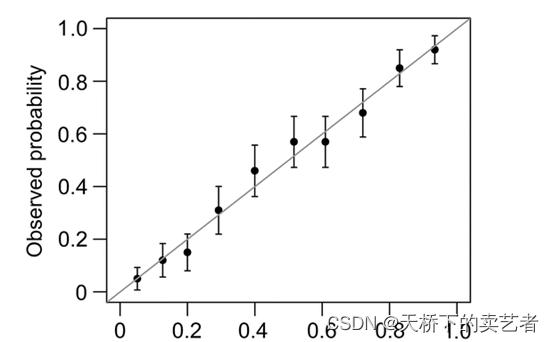
另外一种是calibration函数重抽样绘制连续的校准图
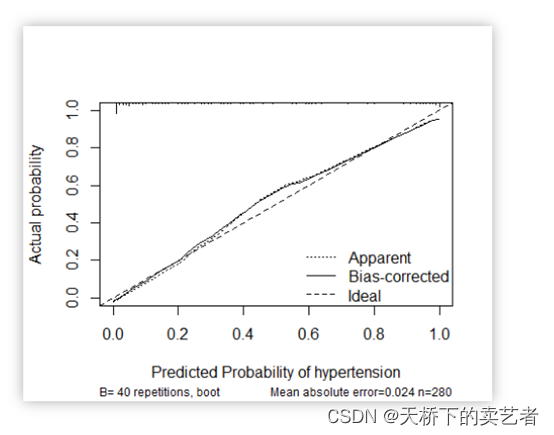
我们既往文章《手动绘制logistic回归预测模型校准曲线》已经进行了手动绘制logistic回归预测模型校准曲线,今天继续视频来介绍外部数据的校准曲线验证和分类数据的校准曲线
R语言手动绘制logistic回归预测模型校准曲线(Calibration curve)(2)
代码
library(ggplot2)
library(rms)
source("E:/r/test/ggfit.R")
#公众号:零基础说科研,公众号回复:早产数据,可以获得数据
#公众号回复:代码,可以获得我自写gg2函数
bc<-read.csv("E:/r/test/zaochan.csv",sep=',',header=TRUE)
#########
bc$race<-ifelse(bc$race=="black",1,ifelse(bc$race=="white",2,3))
bc$smoke<-ifelse(bc$smoke=="nonsmoker",0,1)
bc$race<-factor(bc$race)
bc$ht<-factor(bc$ht)
bc$ui<-factor(bc$ui)
###
set.seed(123)
tr1<- sample(nrow(bc),0.6*nrow(bc))##随机无放抽取
bc_train <- bc[tr1,]#60%数据集
bc_test<- bc[-tr1,]#40%数据集
##
fit<-glm(low ~ age + lwt + race + smoke + ptl + ht + ui + ftv,family = binomial("logit"),data = bc_train )
pr1<- predict(fit,type = c("response"))#得出预测概率
#外部数据生成概率
pr2 <- predict(fit,newdata= bc_test,type = c("response"))
#生成两个数据的结局变量
y1<-bc_train[, "low"]
y2<-bc_test[, "low"]
###
plot1<-gg2(bc_train,pr1,y1)
ggplot(plot1, aes(x=meanpred, y=meanobs)) + geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se), width=.02)+annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+expand_limits(x = 0, y = 0) + scale_x_continuous(expand = c(0, 0)) + scale_y_continuous(expand = c(0, 0))+geom_point(size=3, shape=21, fill="white")+xlab("预测概率")+ylab("实际概率")
##
plot2<-gg2(bc_test,pr2,y2)
ggplot(plot2, aes(x=meanpred, y=meanobs)) + geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se), width=.02)+annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+expand_limits(x = 0, y = 0) + scale_x_continuous(expand = c(0, 0)) + scale_y_continuous(expand = c(0, 0))+geom_point(size=3, shape=21, fill="white")+xlab("预测概率")+ylab("实际概率")
#########
# 假设我们想了解吸烟人群和不吸烟人群比较,模型的预测能力有什么不同,可以把原数据分成2个模型,分别做成校准曲线,然后进行比较,
# 先分成吸烟组和不吸烟组两个数据
dat0<-subset(bc,bc$smoke==0)
dat00<-dat0[,-6]
dat1<-subset(bc,bc$smoke==1)
dat11<-dat1[,-6]
##
fit0<-glm(low ~ age + lwt + race + ptl + ht + ui + ftv,family = binomial("logit"),data = dat00)
fit1<-glm(low ~ age + lwt + race + ptl + ht + ui + ftv,family = binomial("logit"),data = dat11)
##
pr0<- predict(fit0,type = c("response"))#得出预测概率
y0<-dat00[, "low"]
pr1<- predict(fit1,type = c("response"))#得出预测概率
y1<-dat11[, "low"]
###
# 做分类的时候有5个参数,前面3个是数据,概率和Y值,group = 2是固定的,
# leb = "nosmoke"是你想给这个分类变量取的名字,生成如下数据
smoke0<-gg2(dat00,pr0,y0,group = 2,leb = "nosmoke")
#接下来做吸烟组的数据
smoke1<-gg2(dat11,pr1,y1,group = 2,leb = "smoke")
#把两个数据合并最后生成绘图数据
plotdat<-rbind(smoke0,smoke1)
#生成了绘图数据后就可以绘图了,只需把plotdat放进去其他不用改,当然你想自己调整也是可以的
ggplot(plotdat, aes(x=meanpred, y=meanobs, color=gro,fill=gro,shape=gro)) + geom_line() +geom_point(size=4)+annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+expand_limits(x = 0, y = 0)
###美化
ggplot(plotdat, aes(x=meanpred, y=meanobs, color=gro,fill=gro,shape=gro)) + geom_line() +geom_point(size=4)+annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+expand_limits(x = 0, y = 0)+scale_x_continuous(expand = c(0, 0)) + scale_y_continuous(expand = c(0, 0))+xlab("predicted probability")+ylab("actual probability")+theme_bw()+theme(panel.grid.major = element_blank(),panel.grid.minor = element_blank())+theme(legend.justification=c(1,0), legend.position=c(1,0))
##我们还可以做出带可信区间的分类校准曲线
smoke0<-gg2(dat00,pr0,y0,group = 2,leb = "nosmoke",g=5)
smoke1<-gg2(dat11,pr1,y1,group = 2,leb = "smoke",g=5)
plotdat<-rbind(smoke0,smoke1)ggplot(plotdat, aes(x=meanpred, y=meanobs, color=gro,fill=gro)) + geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se,), width=.02)+geom_point(size=4)+annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+expand_limits(x = 0, y = 0)+scale_x_continuous(expand = c(0, 0)) + scale_y_continuous(expand = c(0, 0))+xlab("predicted probability")+ylab("actual probability")+theme_bw()+theme(panel.grid.major = element_blank(),panel.grid.minor = element_blank())+theme(legend.justification=c(1,0),legend.position=c(1,0))
###也可以加入连线,不过我这个数据加入连线感觉不是很美观
ggplot(plotdat, aes(x=meanpred, y=meanobs, color=gro,fill=gro)) + geom_errorbar(aes(ymin=meanobs-1.96*se, ymax=meanobs+1.96*se,), width=.02)+geom_point(size=4)+annotate(geom = "segment", x = 0, y = 0, xend =1, yend = 1)+expand_limits(x = 0, y = 0)+scale_x_continuous(expand = c(0, 0)) + scale_y_continuous(expand = c(0, 0))+xlab("predicted probability")+ylab("actual probability")+theme_bw()+theme(panel.grid.major = element_blank(),panel.grid.minor = element_blank())+theme(legend.justification=c(1,0), legend.position=c(1,0)) +geom_line()
相关文章:

代码+视频,手动绘制logistic回归预测模型校准曲线(Calibration curve)(2)
校准曲线图表示的是预测值和实际值的差距,作为预测模型的重要部分,目前很多函数能绘制校准曲线。 一般分为两种,一种是通过Hosmer-Lemeshow检验,把P值分为10等分,求出每等分的预测值和实际值的差距 另外一种是calibrat…...
实例)
金融数据_Scikit-Learn决策树(DecisionTreeClassifier)实例
金融数据_Scikit-Learn决策树(DecisionTreeClassifier)实例 逻辑回归: 逻辑回归常被用于二分类问题, 比如涨跌预测。你可以将涨跌标记为类别, 然后使用逻辑回归进行训练。 决策树和随机森林: 决策树和随机森林是用于分类问题的强大模型。它们能够处理非线性关系, 并且对于特征…...

bash的login shell与non-login shell,以及各自的初始化过程
识别login shell与non-login shell login shell 可能是以-开头的 [almalinuxVM-AlmaLinux8-tmpl-wanlinwang ~]$ echo $0 -bash # "-" is the first character. Therefore, this is a login shell.或者以--login启动的bash [almalinuxVM-AlmaLinux8-tmpl-wanlinw…...
为什么苹果 Mac 电脑需要使用清理软件?
尽管 Apple Mac 电脑因其卓越的性能、简洁高效的 macOS 操作系统及独特的美学设计备受全球用户青睐,但任何电子设备在长期使用后都难以避免面临系统资源日渐累积的问题。其中一个重要维护需求在于,随着使用时间的增长,Mac电脑可能会由于系统垃…...

33. UE5 RPG使用增强输入激活GameplayAbility(三)
在前面的文章,我们实现了使用GameplayTag和InputAction的对应绑定的数据,并且添加到了增强输入映射的上下文中,实现了通过按键打印对应的GameplayTag,这只是我们基础需要制作的。目的主要是为了实现在GameplayAblity上面设置对应的…...

speech to text 库FastASR交叉编译arm target的配置
FastASR是一个比较方便的SPEECH TO TEXT的AI库。开源。下面介绍下其在交叉编译到ARM target时候的交叉编译的cmake配置: cmake_minimum_required(VERSION 3.10)project(FastASR)SET(CMAKE_C_COMPILER "/home/xxx/buildroot/output/platform_name/host/bin/aar…...
WPS快速将插入Excle数据插入Word
前置条件: 一张有标题、数据的excle表格word中的表格与excle表格标题对应或包含电脑已经安装WPS软件 第一步、根据word模板设计excle模板,标头对应 第二步、word上面选【引用】--【邮件】,选打开数据源,找到excle文件,…...

Springboot 集成Rabbitmq之延时队列
1.首先确保已经引入了Spring AMQP和RabbitMQ的相关依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> </dependency> 2. 创建一个普通队列并设置TTL&#x…...

【云开发笔记NO.22】运用云原生产品打造技术中台
一、云原生产品与技术中台的结合点 云原生产品以其容器化、微服务化、自动化等特性,为技术中台的建设提供了强大的技术支持。容器化技术使得应用可以更容易地进行部署和管理,提高了应用的可移植性和弹性。微服务架构则让应用更加模块化,便于…...
C++进阶(五) 哈希
1. unordered系列关联式容器 1.1 unordered_map 1.2 unordered_map的接口说明 2. 底层结构 2.1 哈希概念 2.2 哈希冲突 2.3 哈希函数 2.4 哈希冲突解决 2.4.1 闭散列 2.4.2 开散列 3. 模拟实现 3.1 unordered_set 3.2 unordered_map 4.哈希的应用 4.1 位图 4.1.…...

【算法基础】基于异或的排序、基于异或的经典面试题
文章目录 1. 传统交换2. 异或与异或的规律3. 基于异或的排序4. 需要注意的地方5. 经典面试题15.1 题目5.2 思路5.3 实现 6. 经典面试题26.1 题目6.2 思路6.3 实现 1. 传统交换 传统交换方法如下: def swap(i, j):tmp ii jj tmp通过开辟一个额外的变量空间&…...

HTML2:列表和表格
列表 有序列表 ordered list ol 无序列表 unordered list ul 定义列表 definition list dl 1,有序列表 每条列表前自带一个序号 2,无序列表 每条列表前自带一个小圆点 3,定义列表 注意:dl中放的不是li列表而是dt列表和dd表项 dt代表术语标题 dd代表术语内容 一个…...

用于无人机小型化设计的高精度温补晶振
用于无人机小型化设计的高精度温补晶振:TG2016SMN和TG2520SMN。无人机的发展可以说是非常的迅速,在安防,农业,交通,电力,直播等领域经常能看到无人机大显身手。无人机的应用场最是非常的广泛,功能更强&…...

轨迹规划 | 图解最优控制LQR算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 最优控制理论2 线性二次型问题3 LQR的价值迭代推导4 基于差速模型的LQR控制5 仿真实现5.1 ROS C实现5.2 Python实现5.3 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全…...
工业视觉检测
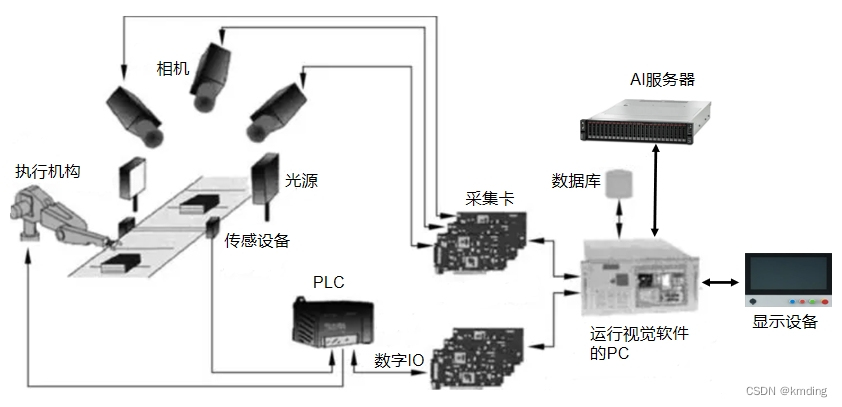
目录 我对工业视觉检测的了解 一、关键组成部分 二、应用场景 三、技术挑战 我对工业视觉检测的了解 工业视觉检测是利用机器视觉技术对产品质量进行自动化检查的过程,它在制造业中扮演着至关重要的角色,用于确保产品质量、提高生产效率、减少人工成…...

wheeltec轮趣ROS教育机器人的网络连接
一、术语解析 宿主机:宿主机是指物理主机,比如用于开发测试的笔记本电脑和台式机电脑。 虚拟机:虚拟机是指安装在宿主机的VMware,推荐在宿主机上安装虚拟机,官方提供虚拟机的镜像以及配套的开发环境。 ROS主机&…...
【Linux ARM 裸机】开发环境搭建
1、Ubuntu 和 Windows 文件互传 使用过程中,要频繁进行 Ubuntu 和 Windows 的文件互传,需要使用 FTP 服务; 1.1、开启 Ubuntu 下的 FTP 服务 //安装 FTP 服务 sudo apt-get install vsftpd //修改配置文件 sudo vi /etc/vsftpd.conf//重启…...

怎么保证缓存与数据库的最终一致性?
目录 零.读数据的标准操作 一.Cache aside Patten--旁路模式 二.Read/Write Through Pattern--读写穿透 三.Write Back Pattern--写回 四.运用canal监听mysql的binlog实现缓存同步 零.读数据的标准操作 这里想说的是不管哪种模式读操作都是一样的,这是一种统一…...
免费SSL通配符证书/SSL泛域名证书获取教程
我们先基本了解什么是SSL证书以及其作用。SSL证书是一种数字证书,它通过为网站提供身份验证和数据加密服务,从而保护网站的用户信息安全。当我们在浏览器的地址栏看到“https”和绿色锁标志时,就表示该网站使用了SSL证书。 那么什么又是通配…...

mysql结构与sql执行流程
Mysql的大体结构 客户端:用于链接mysql的软件 连接池: sql接口: 查询解析器: MySQL连接层 连接层: 应用程序通过接口(如odbc,jdbc)来连接mysql,最先连接处理的是连接层。 连接层…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
