【数据结构】模拟实现 堆
堆数据结构是一种数组对象,它可以被看作一颗完全二叉树的结构(数组是完全二叉树),堆是一种静态结构。
堆分为最大堆和最小堆。
最大堆:每个父结点都大于孩子结点。
最小堆:每个父结点都小于孩子结点。
堆的优势:效率高,可以找最大数最小数,增删的时间复杂度为lgN
怎么找最后一个叶子结点?
找到最后一个叶子结点(左孩子为空就是叶子结点),由于堆是静态结构,所以我们要通过计算下标的方法找,计算它的孩子是否超出了数组范围。
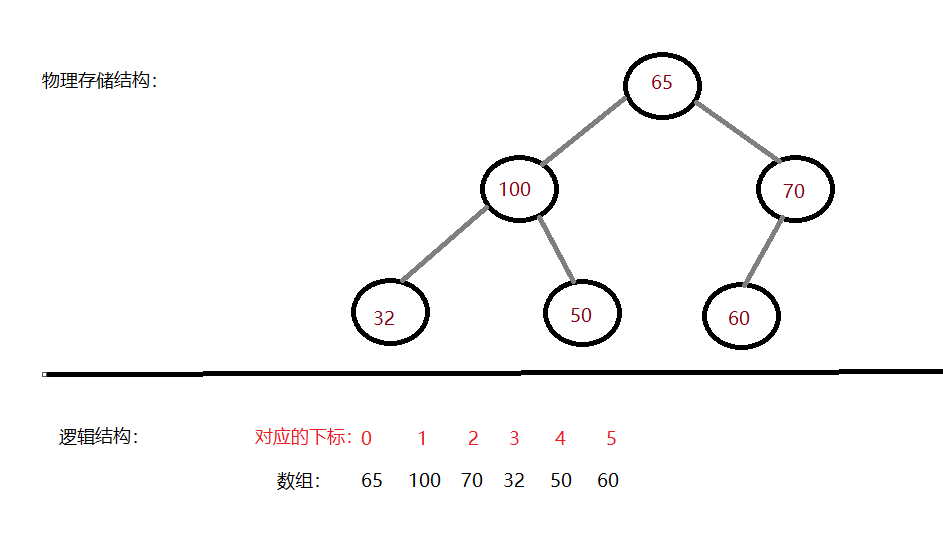
通过观察可以总结数组下标计算父子关系的公式:
leftchild = parent*2 +1
rightchild = parent*2+ 1
parent =( child -1) /2
1.代码实现:
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;}HP;
Heap结构体中有一个指向动态数组的指针,size表示数组的当前元素个数,capacity表示数组的容量
将结构体的定义和函数的申明都放在Heap.h中:
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;}HP;//以数组的形式打印堆的元素
void PrintHeap(HP* php);
//初始化堆
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);//插入数据x 但是要依旧保持堆的形态
void HeapPush(HP* php, HPDataType x);//删除堆顶的元素
void HeapPop(HP* php);//返回堆顶的元素
HPDataType HeapTop(HP* php);
//判定堆是否为空
bool HeapEmpty(HP* php);
//返回堆当前元素的个数
int HeapSize(HP* php);在Heap.c文件中完成接口的实现:
初始化:
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;}插入元素:
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0) {if (a[child] < a[parent]) {Swap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; }else {break;}}
}
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity) //检查容量{int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}HeapPush函数::插入元素将对象的指针传过来并且将要插入的元素传过来,插入元素前检查容量当size ==capacity时就得扩容,我们采用的是将原来的容量扩大两倍,因为两倍比较合适。定义一个新的容量当之前的容量为0时给4个字节的大小,之前有容量时扩大到原来的两倍。这里需要注意的时realloc是在原来的基础上扩大的字节数所以要记得newcapacity*sizeof(HPDataType)!再将a指向扩容后的地址然后更新capacity的大小,在size位置插入元素x,然后size++。在这里模拟实现的是小堆,但是插入数据的位置在逻辑结构的数组的尾部,或者说是在完全二叉树的叶子节点位置。小堆结构的最小的元素都在较上方,所以说要向上调整。将数组的指针和插入元素的数组下标传给向上调整函数。
AdjustUp函数::通过公式计算出插入元素的数组下标的父节点的数组下标。
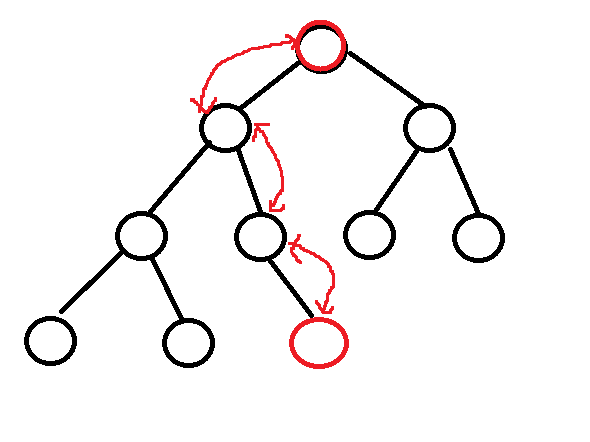
假设插入的位置在最下方的红色部分,小堆就是父节点要比子节点的值小,如果插入的元素的值很小,需要一直和当前位置的父节点交换位置,那交换最多的情况就是从叶子节点的位置交换到根节点的位置(也就是说child=0时),因为交换的次数不确定所以放到for不好控制,所以将向上调整的动作放到while循环里,当符合条件时跳出循环即可。当child>0时,a[child] < a[parent]所以进行交换,将parent的下标的值给child,然后再次计算出该节点位置的父节点的数组下标,再次比较该节点与其父节点的值的大小,如果符合调整的条件就进行交换,一直循环。当child==0或者a[parent]>=a[parent]的值就不需要就跳出循环,向上调整结束,新插入的元素就到了应该到的位置。
Swap函数::取出要交换的值的地址交给该函数,创建一个同类型的变量tmp存储p1指向的内容,p1再指向p2所指向的内容,最后再将p2指向tmp就完成了值的交换。
通过这三个函数就完成了数据的插入,同时保持了堆的形态。
删除堆顶的元素:
首先明白小堆和大堆的应用时为了找到前n个最小或者最大的元素,删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
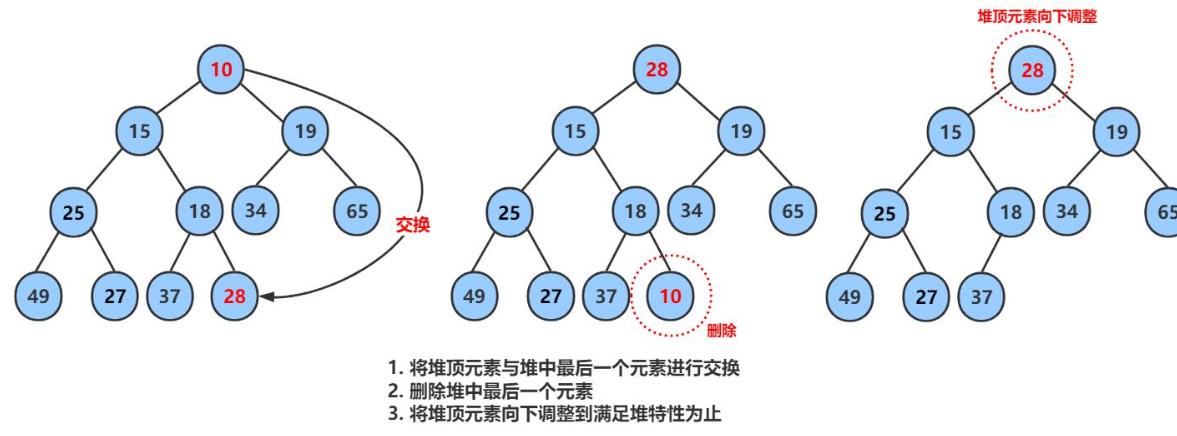
void AdjustDown(HPDataType* a, int n, int parent)
{int minChild = parent * 2 + 1; //默认最小的孩子是左孩子while (minChild < n){if (minChild + 1 < n && a[minChild + 1] < a[minChild]){minChild++; }if (a[minChild] < a[parent]) {Swap(&a[minChild], &a[parent]); parent = minChild; minChild = parent * 2 + 1; }else {break;}}}
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]); //将根部元素与最后一个元素交换,然后再向下调整php->size--; //相当于删除了最后一个元素AdjustDown(php->a, php->size, 0);
}
删除堆顶元素,首先保证堆有元素,再交换堆顶元素和最后一个元素,size--就相当于删除了最后一个元素,再调用向下调整函数。将数组的地址和数组的元素个数还有数组的首元素下标传给向下调整函数,开始调整。模拟实现的是小堆所以较大的元素在堆的下方,小的元素在较上方,每一个父节点都有两个子节点所以该和谁交换使得根节点的数据往下调整呢?? 首先根据父节点的数组下标得出左孩子的数组下标,默认最小孩子minChild为左孩子,如果右孩子比左孩子小那就让minChild+1将这个调整最小孩子的动做放到while循环中,因为每一次调整都得和最小孩子交换位置。循环调整的停止条件是minChild小于n因为要保证交换的元素下标是在数组范围内的不能越界交换(这个条件也是循环最多次的条件)。
当a[minChild] < a[parent]时就进行交换调整。当父亲和最小孩子的值相等或者小于最小孩子的值 那就跳出循环 向下调整完成。
打印堆元素(以数组的形式打印)
void PrintHeap(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}判空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
取堆顶元素
//返回堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}销毁
void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
2.测试用例:
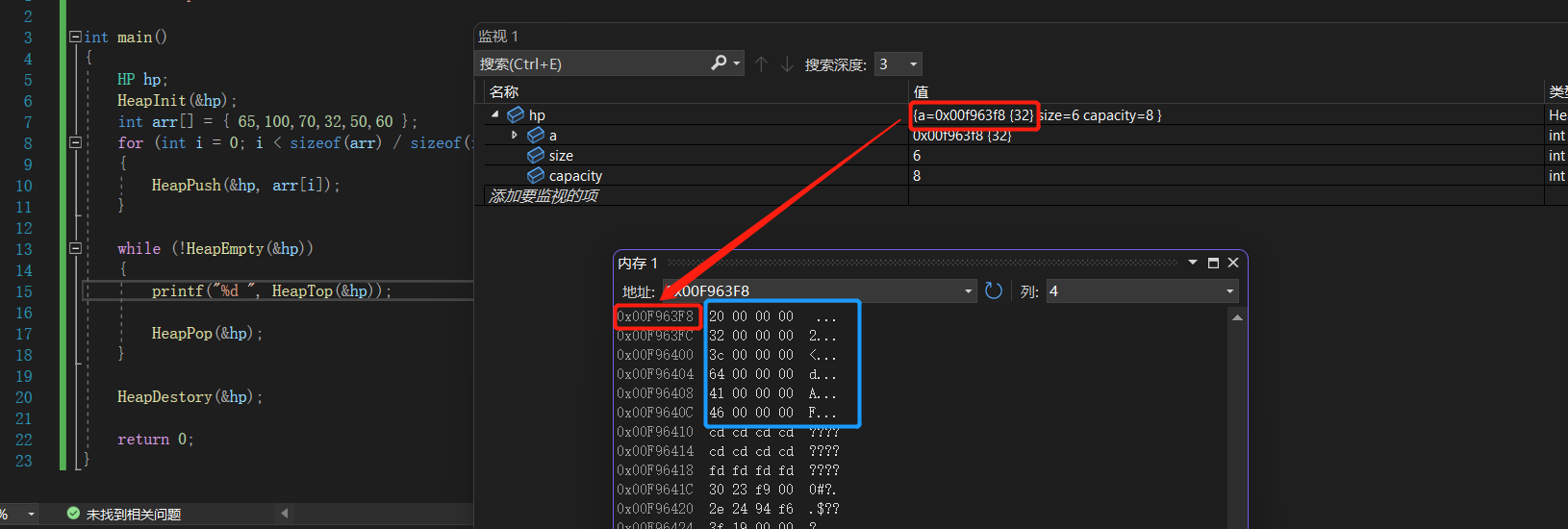
#include"Heap.h"int main()
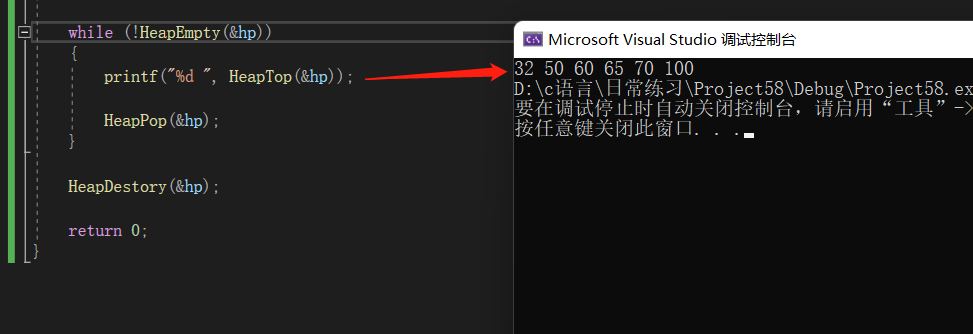
{HP hp;HeapInit(&hp);int arr[] = { 65,100,70,32,50,60 };for (int i = 0; i < sizeof(arr) / sizeof(int); i++){HeapPush(&hp, arr[i]);}while (!HeapEmpty(&hp)) //不为空时{printf("%d ", HeapTop(&hp)); //打印堆顶的元素HeapPop(&hp); //删除堆顶的元素 三行代码就实现了出堆,调整,打印堆顶元素} //一直循环直到堆为空时循环停止HeapDestory(&hp); //销毁堆return 0;
}
3.整体代码:
test.c:
#include"Heap.h"int main()
{HP hp;HeapInit(&hp);int arr[] = { 65,100,70,32,50,60 };for (int i = 0; i < sizeof(arr) / sizeof(int); i++){HeapPush(&hp, arr[i]);}while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}HeapDestory(&hp);return 0;
}Heap.c:
#include"Heap.h"void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;}
void HeapDestory(HP* php)
{free(php->a);php->a = NULL;}void PrintHeap(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0) //最坏的情况是孩子一直向上调整 ,最大的范围就是到了数组的第一个位置{if (a[child] < a[parent]) //大小堆在这里调整 插入的元素在最后一个 小堆:< 大堆: >{Swap(&a[child], &a[parent]); //交换孩子和父亲的值child = parent; //再将之前父亲的位置给孩纸,parent = (child - 1) / 2; //相当于现在是孙子和爷爷位置的比较}else //当孩子大于等于父亲的值时就不用调整了,可以退出循环{break;}}
}void AdjustDown(HPDataType* a, int n, int parent)//向下调整 数组传过来 数组的大小 根节点的下标
{int minChild = parent * 2 + 1; //默认最小的孩子是左孩子while (minChild < n){if (minChild + 1 < n && a[minChild + 1] < a[minChild]){minChild++; //当右孩子比左孩子小 那么最小的孩子就变为右孩子}if (a[minChild] <a[parent]) //当父亲比孩子大时 ,那父亲就要和孩子交换位置{Swap(&a[minChild], &a[parent]); //调用交换函数 交换值parent = minChild; //交换完成后父亲还要继续和下边的孩子比较 ,将最小孩子的位置给给父亲minChild = parent * 2 + 1; //父亲来到了上一个最小孩子的位置,此时这个位置的下一行的最小孩子又默认为左孩子继续比较 }else //当父亲和最小孩子的值相等或者小于最小孩子的值 那就跳出循环 向下调整完成{break;}}}//插入x 保持堆形态
void HeapPush(HP* php, HPDataType x) //用结构体的指针接收对象的指针 接收 最后一个元素
{assert(php);if (php->size == php->capacity) //检查容量{int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1); //传过去对象的指针 和对象的最后一个元素
}//删除堆顶的元素----为了找到次大的元素
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]); //将根部元素与最后一个元素交换,然后再向下调整php->size--; //相当于删除了最后一个元素AdjustDown(php->a, php->size, 0);
}//返回堆顶的元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;}int HeapSize(HP* php)
{assert(php);return php->size;
}Heap.h
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;}HP;void PrintHeap(HP* php);void HeapInit(HP* php);
void HeapDestory(HP* php);//插入数据x 继续保持堆的形态
void HeapPush(HP* php, HPDataType x);//删除堆顶的元素
void HeapPop(HP* php);//返回堆顶的元素
HPDataType HeapTop(HP* php);bool HeapEmpty(HP* php);int HeapSize(HP* php);相关文章:

【数据结构】模拟实现 堆
堆数据结构是一种数组对象,它可以被看作一颗完全二叉树的结构(数组是完全二叉树),堆是一种静态结构。堆分为最大堆和最小堆。最大堆:每个父结点都大于孩子结点。最小堆:每个父结点都小于孩子结点。堆的优势…...
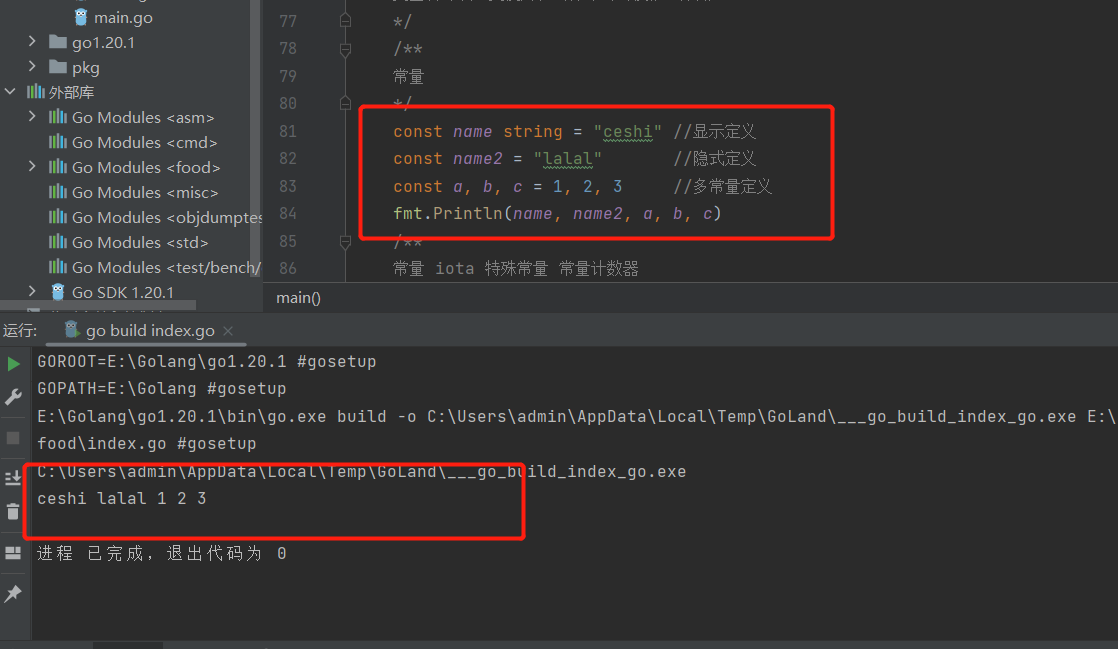
Go语言学习的第三天--上部分(基础用法)
前两天经过不断度娘,与对up主的跟踪学习了解了go的历史,今天开始了go的基础!!本章主要是go 的注释、变量及常量的梳理一、注释不管什么语言都有自己的注释,go也不例外 !!单行注释 // 多行注释 …...
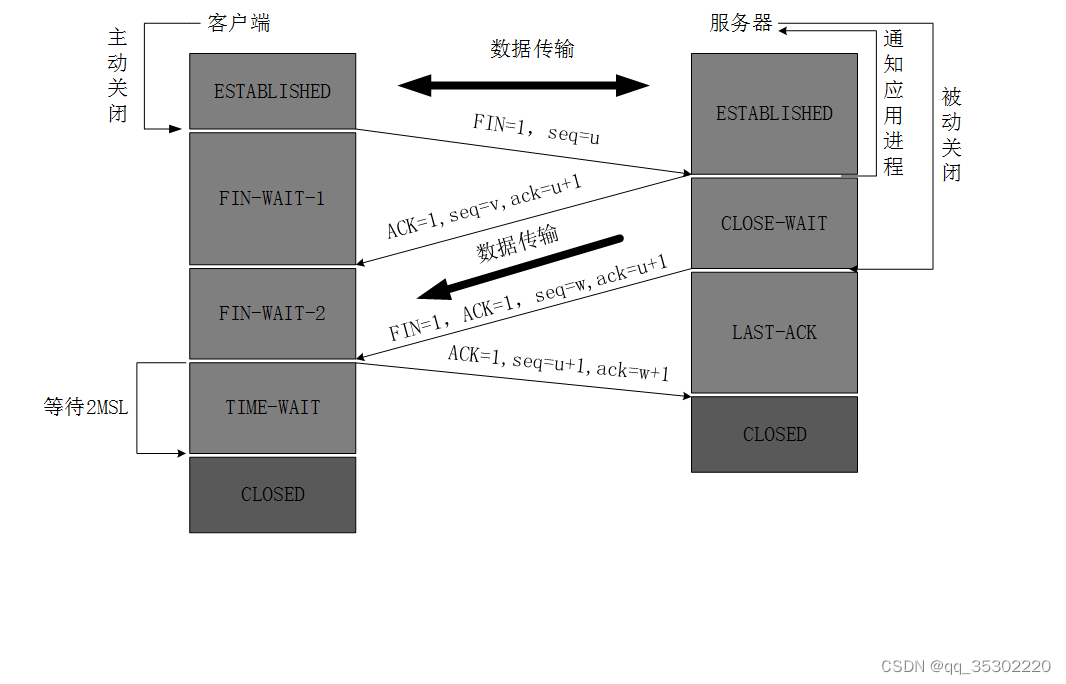
linux面试基础篇
题目目录1.简述DNS分离解析的工作原理,关键配置2.apache有几种工作模式,分别简述两种工作模式及其优缺点?3.写出172.0.0.38/27 的网络id与广播地址4.写出下列服务使用的传输层协议(TCP/UDP)及默认端口5.在局域网想获得…...
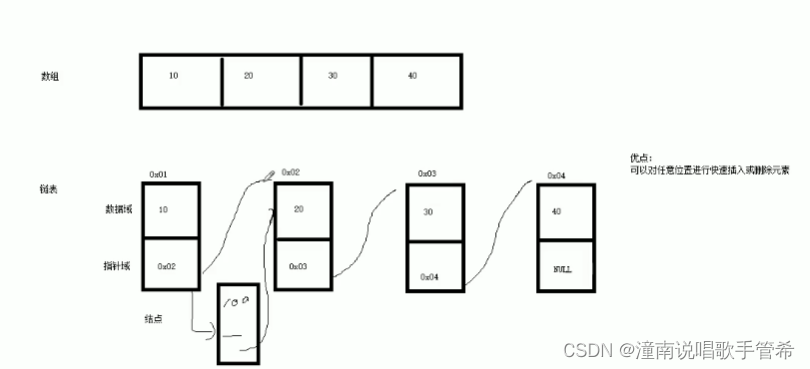
黑马程序员提高变成
这里写目录标题函数模板1.2.2 函数模板注意事项1.2.3 函数模板案例调用规则类模板与函数模板区别类模板与继承类模板成员函数类外实现#pragma once类模板与友元案例重新定义【】stl2.2 STL基本概念STL六大组件容器算法迭代器初识vectorvector容器嵌套容器string容器string赋值操…...

MySQL5种索引类型
MySQL的类型主要有五种:主键索引、唯一索引、普通索引、空间索引、全文索引 有表: CREATE TABLE t1 ( id bigint unsigned NOT NULL AUTO_INCREMENT, u1 int unsigned NOT NULL DEFAULT 0, u2 int unsigned NOT NULL DEFAULT 0, u3 varchar(20) NOT NU…...

uniapp封装缓存方法,支持类似cookie具有过期时间
1、定义CacheManage类,有set和get方法 class CacheManage {set() {},get() {} }set用来设置缓存,get用来获取缓存 2、完善set业务逻辑 大概逻辑如下: 1、将接收params参数,包含key、data、unit、time key 缓存字段,…...
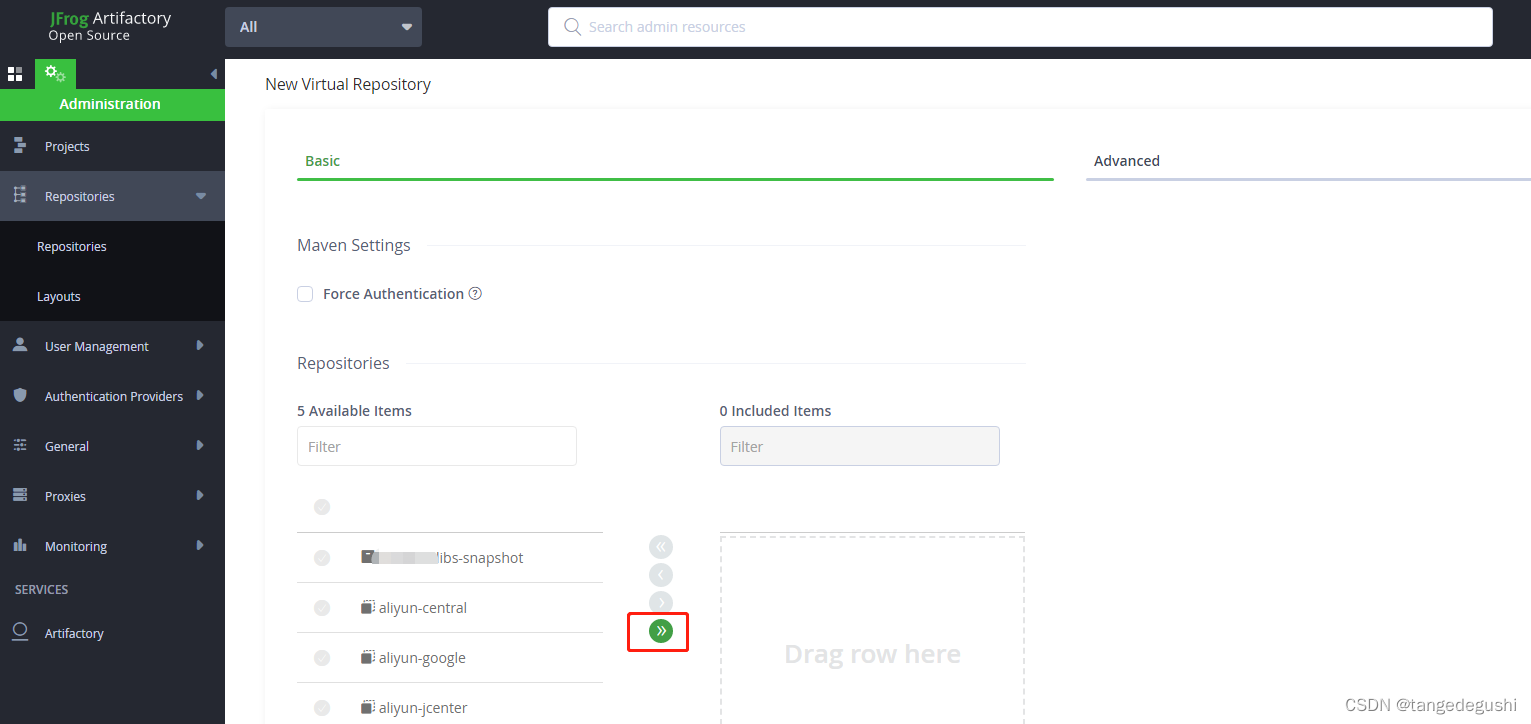
Jfrog 搭建本地maven仓库以及上传Android库
Jfrog 下载 安装包下载地址:Download Artifactory OSS | JFrog 如果是想下载之前的版本,可以点击上面的Get code source ,如果是最新版本,直接点下面的下载就好。下面以Linux安装为例。 Jfrog安装 对于Linux而言,其实…...
日报周报月报工作总结生成器【智能文案生成器】
日报周报月报工作总结生成器【智能文案生成器】 天天写日报,我真的快奔溃了! 摸了一天鱼,下班还要写日报; 划了一周的水,周末还要写周报; 啊啊啊啊… 在职场上,尤其是互联网公司里,…...

linux日志管理工具logrotate配置
linux日志管理工具logrotate配置logrotate介绍logrotate配置讲解主配置文件解释(/etc/logrotate.conf)logrotete 命令参数添加配置以添加一个nginx配置为例强制启动配置logrotate介绍 logrotate是centos自带工具,其他操作系统可能需要自行安装。logrotate用来进行日…...

[ C++ ] 设计模式——单例模式
目录 1.设计模式: 2.单例模式 饿汉模式 懒汉模式 饿汉模式和懒汉模式的优缺点 1.设计模式: 设计模式(Design Pattern)是一套被反复使用,多数人只晓得,经过分类的,代码设计经验的总结。为什么会产生设计模式这样的…...
HACKTHEBOX——Help
nmap可以看到对外开放了22,80,3000端口可以看到80端口和3000端口都运行着http服务,先从web着手切入TCP/80访问web提示无法连接help.htb,在/etc/hosts中写入IP与域名的映射打开只是一个apache default页面,没什么好看的使用gobuster扫描网站目…...
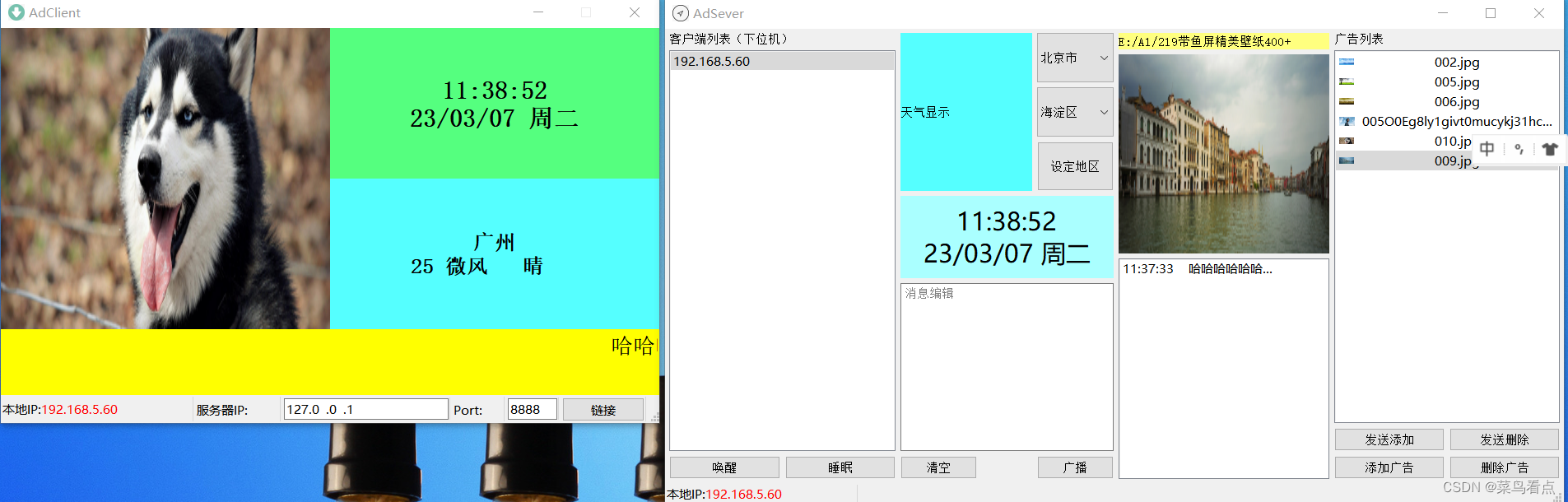
Qt广告机客户端(下位机)
目录功能结构adClient.promain.cppadclient.h 客户端adclient.cpp 客户端addate.h 时间处理addate.cpp 时间处理adsocket.h 客户端Socket处理adsocket.cpp 客户端Socket处理weather.h 天气信息处理weather.cpp 天气信息处理rollmassege.h 滚动信息处理rollmassege.cpp 滚动信息…...

JavaScript新手学习手册-基础代码(二)
与上篇博客相接 一:函数: 案例:通过函数实现绝对值的输出 方法一: function absoluate(x){if(x>0){return x;}else{ return -x;}} 在控制台调用函数 方法二: var demo1 function(x){if(x>0){return x;}els…...
wireshark 抓包使用记录
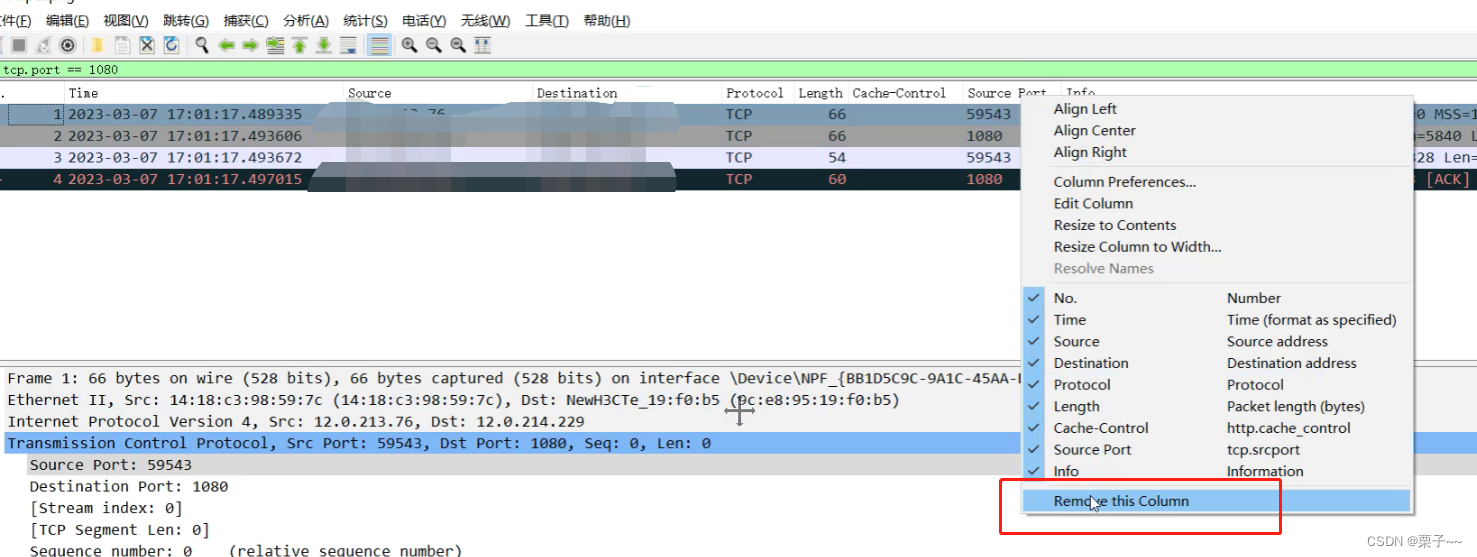
文章目录前言wireshark 抓包使用记录一、wireshark的基础使用二、wireshark的常用功能1、开始混杂模式2、过滤器操作2.1、抓包过滤器2.2、显示过滤器3、时间格式显示4、统计流量图5、标记显示6、导出数据包7、增加、隐藏、删除显示列前言 如果您觉得有用的话,记得给…...

pd dataframe 读取处理 有合并单元格的excel方式
from pathlib import Path import openpyxl 拆分所有的合并单元格,并赋予合并之前的值。 由于openpyxl并没有提供拆分并填充的方法,所以使用该方法进行完成 def unmerge_and_fill_cells(worksheet): all_merged_cell_ranges list( worksheet.merged_…...
七,iperf3源代码分析:状态机及状态转换过程--->运行正向TCP单向测试时的服务端代码
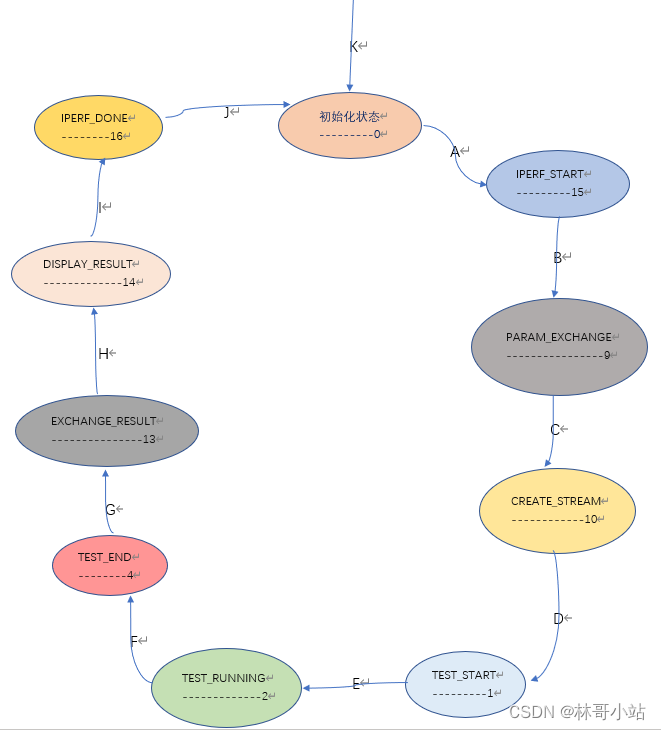
本文目录一、测试用命令二、iperf3状态机中各个状态解析三、iperf3状态机迁移分析K-初始化测试对象(NA--->初始化状态):A-服务器端测试对象开始运行(初始化状态--->IPERF_START状态):B-建立控制连接(初始化状态-…...

【网络篇】----- 传输层协议 之 UDP(协议格式,协议特性和编程影响三方面详细分析)
文章目录 前言1、UDP协议2、协议格式 2.1、协议格式模型2.2、字段分析3.协议特性4.编程影响总结前言 1、UDP协议 UDP协议,又名数据报传输协议,是传输层协议之一!!! 在TCP/IP五层模型中,在传输层中ÿ…...

【基于STM32的多功能台灯控制】
基于STM32的多功能台灯控制 在之前一篇博文中已出过智能台灯相关的介绍,在这里对之前的模块以及功能上进行了优化和功能上的改进,需源码或实物可私【创作不易-拒绝白嫖】 功能说明 1、按键模式多功能台灯在设计上使用了4个按键分别做为 按键1模式的切换…...

Mac 编译x264源码No working C compiler found 错误
在mac上编译x264源码时,报错No working C compiler found 。网上找了一圈方案也无法解决 只能硬着头皮看configure这个脚本,通过一步一步抽丝拨茧终于是在mac上可以编译了。 这里只当记录一下,为后续同学遇到同样问题提供一个辅助解决方案。…...
如何有效地降低软件开发风险?
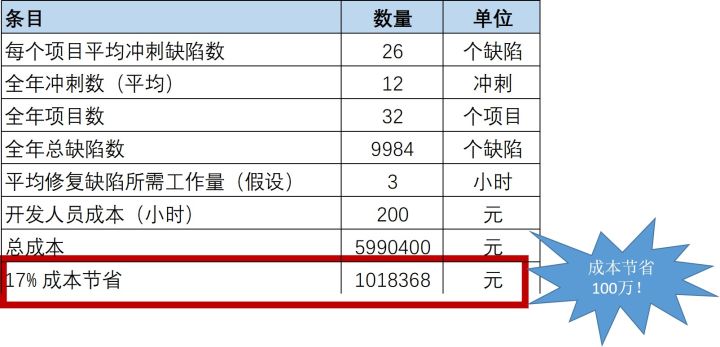
1、科学分析风险 高风险自动预警 一般对风险进行科学分析,主要从3个维度进行划分:影响的严重性、发生的可能性、产生的影响性。 根据风险对项目的影响程度,从3个维度将其划分5个等级:很低、比较低、中等、比较高、很高。这样我们能…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
