多叉树题目:子树中标签相同的结点数
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:子树中标签相同的结点数
出处:1519. 子树中标签相同的结点数
难度
5 级
题目描述
要求
给你一个树(即一个连通的无向无环图),这个树由编号从 0 \texttt{0} 0 到 n − 1 \texttt{n} - \texttt{1} n−1 的 n \texttt{n} n 个结点和 n − 1 \texttt{n} - \texttt{1} n−1 条边 edges \texttt{edges} edges 组成。树的根结点为结点 0 \texttt{0} 0,树中的每一个结点都有一个标签,标签是字符串 labels \texttt{labels} labels 中的一个小写字符(编号为 i \texttt{i} i 的结点的标签是 labels[i] \texttt{labels[i]} labels[i])。
边数组 edges \texttt{edges} edges 以 edges[i] = [a i , b i ] \texttt{edges[i] = [a}_\texttt{i}\texttt{, b}_\texttt{i}\texttt{]} edges[i] = [ai, bi] 的形式给出,该格式表示结点 a i \texttt{a}_\texttt{i} ai 和 b i \texttt{b}_\texttt{i} bi 之间存在一条边。
返回一个大小为 n \texttt{n} n 的数组 ans \texttt{ans} ans,其中 ans[i] \texttt{ans[i]} ans[i] 表示第 i \texttt{i} i 个结点的子树中与结点 i \texttt{i} i 标签相同的结点数。
树 T \texttt{T} T 的子树是由 T \texttt{T} T 中的某个结点及其所有后代结点组成的树。
示例
示例 1:

输入: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd" \texttt{n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"} n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出: [2,1,1,1,1,1,1] \texttt{[2,1,1,1,1,1,1]} [2,1,1,1,1,1,1]
解释:结点 0 \texttt{0} 0 的标签为 ‘a’ \texttt{`a'} ‘a’ ,以 ‘a’ \texttt{`a'} ‘a’ 为根结点的子树中,结点 2 \texttt{2} 2 的标签也是 ‘a’ \texttt{`a'} ‘a’,因此答案为 2 \texttt{2} 2。注意树中的每个结点都是这个子树的一部分。
结点 1 \texttt{1} 1 的标签为 ‘b’ \texttt{`b'} ‘b’,结点 1 \texttt{1} 1 的子树包含结点 1 \texttt{1} 1、 4 \texttt{4} 4 和 5 \texttt{5} 5,由于结点 4 \texttt{4} 4、 5 \texttt{5} 5 的标签与结点 1 \texttt{1} 1 不同,因此答案为 1 \texttt{1} 1(该结点本身)。
示例 2:
输入: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb" \texttt{n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"} n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出: [4,2,1,1] \texttt{[4,2,1,1]} [4,2,1,1]
解释:结点 2 \texttt{2} 2 的子树中只有结点 2 \texttt{2} 2,因此答案为 1 \texttt{1} 1。
结点 3 \texttt{3} 3 的子树中只有结点 3 \texttt{3} 3,因此答案为 1 \texttt{1} 1。
结点 1 \texttt{1} 1 的子树中包含结点 1 \texttt{1} 1 和 2 \texttt{2} 2,标签都是 ‘b’ \texttt{`b'} ‘b’,因此答案为 2 \texttt{2} 2。
结点 0 \texttt{0} 0 的子树中包含结点 0 \texttt{0} 0、 1 \texttt{1} 1、 2 \texttt{2} 2 和 3 \texttt{3} 3,标签都是 ‘b’ \texttt{`b'} ‘b’,因此答案为 4 \texttt{4} 4。
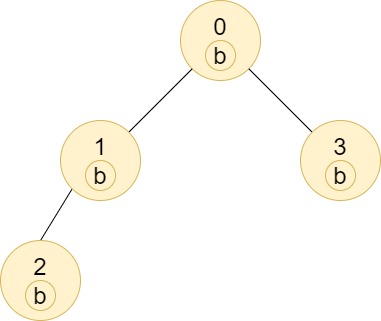
示例 3:
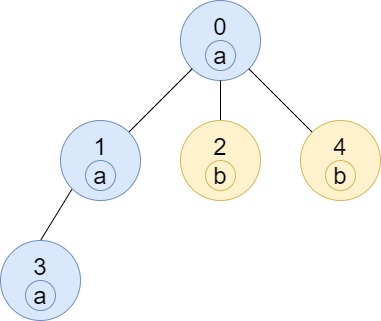
输入: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab" \texttt{n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"} n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出: [3,2,1,1,1] \texttt{[3,2,1,1,1]} [3,2,1,1,1]
数据范围
- 1 ≤ n ≤ 10 5 \texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{5} 1≤n≤105
- edges.length = n − 1 \texttt{edges.length} = \texttt{n} - \texttt{1} edges.length=n−1
- edges[i].length = 2 \texttt{edges[i].length} = \texttt{2} edges[i].length=2
- 0 ≤ a i , b i < n \texttt{0} \le \texttt{a}_\texttt{i}\texttt{, b}_\texttt{i} < \texttt{n} 0≤ai, bi<n
- a i ≠ b i \texttt{a}_\texttt{i} \ne \texttt{b}_\texttt{i} ai=bi
- labels.length = n \texttt{labels.length} = \texttt{n} labels.length=n
- labels \texttt{labels} labels 仅由小写英语字母组成
解法
思路和算法
这道题中的树是一个无向无环的连通图,规定根结点是结点 0 0 0,其余结点之间只能知道连通关系。为了得到相邻结点之间的父结点和子结点的关系,需要根据给定的边得到每个结点的相邻结点,然后从根结点开始遍历树。在确定所有相邻结点之间的父结点和子结点的关系之后,即可得到每个子树中包含的结点。对于每个子树,遍历子树中的每个结点即可得到与子树根结点标签相同的结点数。
由于树中的结点数 n n n 最大可达 1 0 5 10^5 105,因此应该尽量避免重复访问结点,而是每个结点都访问一次。由于树中的每个标签的出现次数由树的根结点标签与每个子树中的每个标签的出现次数决定,因此可以使用后序遍历的方式得到每个子树中的每个标签的出现次数,然后得到每个子树中与子树根结点标签相同的结点数。
对于每个子树,需要使用哈希表记录子树中每个标签的出现次数。当子树中只有一个结点时,只有子树根结点的标签出现 1 1 1 次,其余标签都不出现;当子树的根结点有子结点时,将每个子结点对应的每个标签的出现次数加到子树根结点的每个标签的出现次数,最后将子树根结点的标签的出现次数加 1 1 1,即可得到子树中每个标签的出现次数。
实现方面有以下两点说明。
-
由于标签只包含小写英语字母,因此可以使用长度为 26 26 26 的数组代替哈希表记录每个标签的出现次数。
-
遍历过程中需要知道相邻结点之间的父结点和子结点的关系。由于和一个结点相邻的结点只有该结点的父结点和全部子结点,一种方法是在遍历过程中传入当前结点的父结点编号,在遍历与当前结点相邻的结点时跳过父结点,则可确保只会访问当前结点的子结点。
代码
class Solution {String labels;List<Integer>[] adjacentNodes;int[][] counts;public int[] countSubTrees(int n, int[][] edges, String labels) {this.labels = labels;adjacentNodes = new List[n];for (int i = 0; i < n; i++) {adjacentNodes[i] = new ArrayList<Integer>();}for (int[] edge : edges) {int node0 = edge[0], node1 = edge[1];adjacentNodes[node0].add(node1);adjacentNodes[node1].add(node0);}counts = new int[n][26];postorder(0, -1);int[] ans = new int[n];for (int i = 0; i < n; i++) {char c = labels.charAt(i);ans[i] = counts[i][c - 'a'];}return ans;}public void postorder(int node, int parent) {char c = labels.charAt(node);List<Integer> adjacent = adjacentNodes[node];for (int next : adjacent) {if (next == parent) {continue;}postorder(next, node);for (int i = 0; i < 26; i++) {counts[node][i] += counts[next][i];}}counts[node][c - 'a']++;}
}
复杂度分析
-
时间复杂度: O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣),其中 n n n 是树的结点数, Σ \Sigma Σ 是字符集,这道题中 Σ \Sigma Σ 是全部小写英语字母, ∣ Σ ∣ = 26 |\Sigma| = 26 ∣Σ∣=26。后序遍历需要访问每个结点一次,对于每个结点需要 O ( ∣ Σ ∣ ) O(|\Sigma|) O(∣Σ∣) 的时间计算以该结点为根结点的子树中的每个标签的出现次数。
-
空间复杂度: O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣),其中 n n n 是树的结点数, Σ \Sigma Σ 是字符集,这道题中 Σ \Sigma Σ 是全部小写英语字母, ∣ Σ ∣ = 26 |\Sigma| = 26 ∣Σ∣=26。空间复杂度包括存储相邻结点信息的空间、哈希表空间和递归调用的栈空间,存储相邻结点信息的空间是 O ( n ) O(n) O(n),哈希表空间是 O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣),即每个结点需要 O ( ∣ Σ ∣ ) O(|\Sigma|) O(∣Σ∣) 的空间记录以该结点为根结点的子树中的每个标签的出现次数,递归调用的栈空间在最坏情况下是 O ( n ) O(n) O(n),因此空间复杂度是 O ( n × ∣ Σ ∣ ) O(n \times |\Sigma|) O(n×∣Σ∣)。
相关文章:

多叉树题目:子树中标签相同的结点数
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:子树中标签相同的结点数 出处:1519. 子树中标签相同的结点数 难度 5 级 题目描述 要求 给你一个树(即一个连通的无向无环图…...
帝国CMS模板源码整站安装说明(图文)
安装步骤 第一步:先把得到的文件解压缩,把文件通过FTP传到空间里。(请不要把类似www.lengleng.net这个文件夹传到FTP,请传这个大文件夹下面的所有文件夹和文件到空间根目录,请不要上传到2级目录,除非你自己…...

物联网系统未来的发展趋势
一、引言 物联网系统作为新一代的信息技术,正在逐渐改变我们的生活和工作方式。随着物联网技术的不断发展和应用场景的拓展,未来物联网系统的发展趋势将更加明显。本文将从技术、应用、安全等方面探讨物联网系统未来的发展趋势。 二、技术发展趋势 1.…...

基于支持 GPT 的服务的初创公司
Kafkai:多语言长篇内容生成,AI写作的新趋势 介绍 随着生成式预训练 Transformer (GPT) 的出现,技术世界正在见证范式转变。 这种人工智能驱动的创新不仅仅是一种转瞬即逝的趋势,而是一种趋势。 它已成为科技行业的基石,…...
基于springboot实现教师人事档案管理系统项目【项目源码+论文说明】
基于springboot实现IT技术交流和分享平台系统演示 摘要 我国科学技术的不断发展,计算机的应用日渐成熟,其强大的功能给人们留下深刻的印象,它已经应用到了人类社会的各个层次的领域,发挥着重要的不可替换的作用。信息管理作为计算…...

上行上传rsync+inotify
引言 使用inotify通知接口,可以用来监控文件系统的各种变化情况,如文件存取、删除、移动、修改等。利用这一机制,可以非常方便地实现文件异动告警、增量备份,并针对目录或文件的变化及时作出响应。 将inotify机制与rsync工具相结合…...

借助ChatGPT写作:打造学术论文中的亮点与互动
ChatGPT无限次数:点击直达 打造学术论文中的亮点与互动 引言 学术论文是学术界交流思想、探讨问题和展示研究成果的重要形式。如何使学术论文在众多作品中脱颖而出,吸引读者的眼球并激发互动,是每位研究者都关注的问题。本文将介绍如何借助ChatGPT这一…...
)
逐步学习Go-sync.Mutex(详解与实战)
概述 Go中提供了互斥锁:sync.Mutex。sync.Mutex提供了以下方法: type Mutex // 加锁。如果已经有goroutine持有了锁,那么就阻塞等待直到持有锁 func (m *Mutex) Lock()// 尝试加锁。如果加锁成功就返回true,否则返回失败 func (m…...
)
每日三道面试题之 Java并发编程 (一)
1.为什么要使用并发编程 并发编程是一种允许多个操作同时进行的编程技术,这种技术在现代软件开发中非常重要,原因如下: 充分利用多核处理器:现代计算机通常都拥有多核处理器,通过并发编程,可以让每个核心独…...

车身稳定控制系统原理是什么?
车身稳定控制系统(Electronic Stability Control,ESC)是一种先进的车辆动态控制系统,其主要原理是通过传感器监测车辆的各项状态,包括车速、转向角度、侧倾角等,然后通过电子控制单元(ECU&#…...

vue3前端加载动画 lottie-web 的简单使用案例
什么是 Lottie Lottie 是 Airbnb 发布的一款开源动画库,它适用于 Android、iOS、Web 和 Windows 的库。 它提供了一套从设计师使用 AE(Adobe After Effects)到各端开发者实现动画的工具流。 UED 提供动画 json 文件即可, 开发者就…...
基于java+springboot+vue实现的健身房管理系统(文末源码+Lw)23-223
摘 要 传统办法管理信息首先需要花费的时间比较多,其次数据出错率比较高,而且对错误的数据进行更改也比较困难,最后,检索数据费事费力。因此,在计算机上安装健身房管理系统软件来发挥其高效地信息处理的作用…...
10款白嫖党必备的ai写作神器,你都知道吗? #媒体#人工智能#其他
从事自媒体运营光靠自己手动操作效率是非常低的,想要提高运营效率就必须要学会合理的使用一些辅助工具。下面小编就跟大家分享一些自媒体常用的辅助工具,觉得有用的朋友可以收藏分享。 1.飞鸟写作 这是一个微信公众号 面向专业写作领域的ai写作工具&am…...
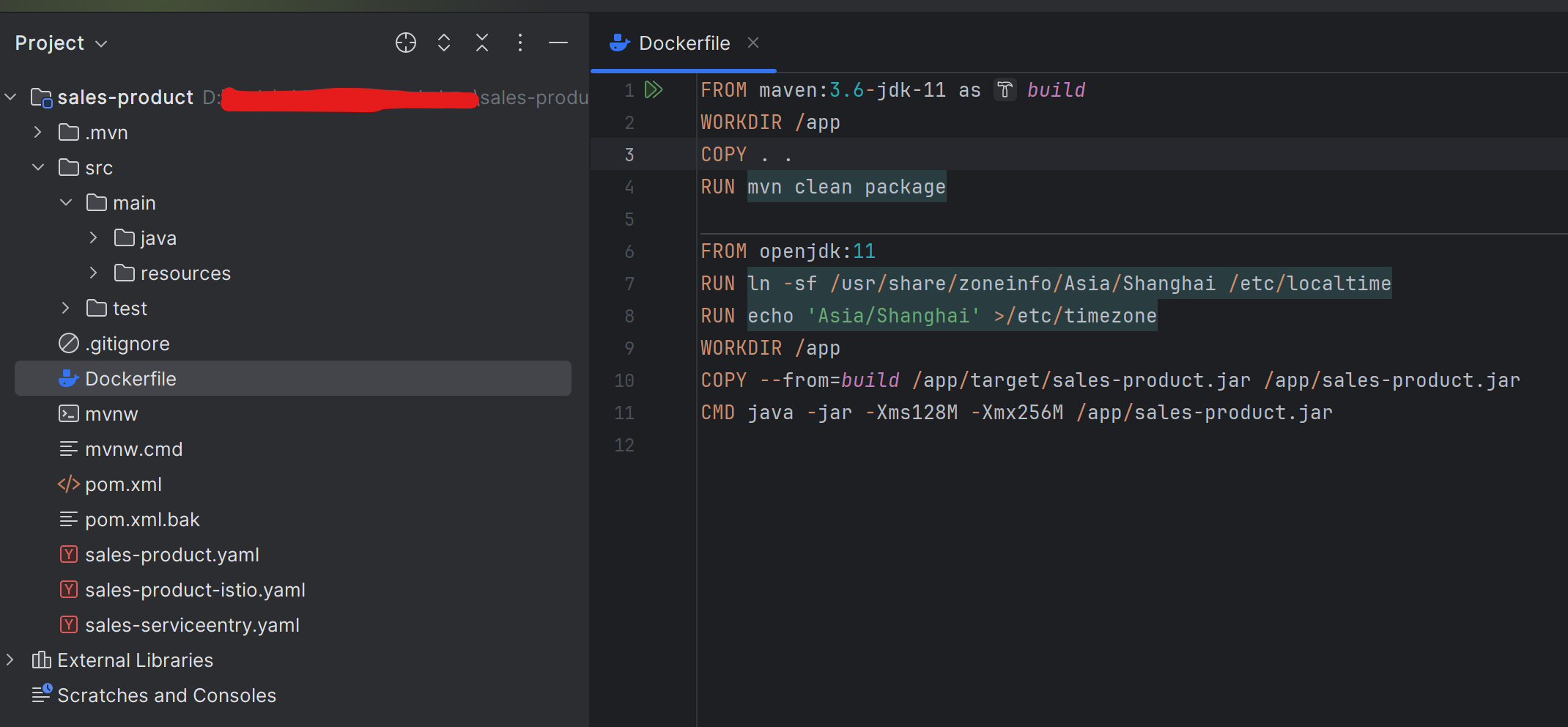
Docker工作流
1.工作流 开发应用编写Dockerfile构建Docker镜像运行Docker容器测试应用发布镜像到Hub迭代更新镜像 2.开发应用 首先你需要创建一个应用,这个应用可以是后端应用或者前端应用,任何语言都可以。 比如:我使用IDEA 创建一个Java后端应用&…...

深入浅出 -- 系统架构之分布式集群的分类
一、单点故障问题 集群,相信诸位对这个概念并不陌生,集群已成为现时代中,保证服务高可用不可或缺的一种手段。 回想起初集中式部署的单体应用,因为只有一个节点,因此当该节点出现任意类型的故障(网络、硬件…...

Docker之镜像与容器的相关操作
目录 一、Docker镜像 搜索镜像 下载镜像 查看宿主机上的镜像 删除镜像 二、Docker容器 创建容器 查看容器 启停容器 删除容器 进入容器 创建/启动/进入容器 退出容器 查看容器内部信息 一、Docker镜像 Docker 运行容器前需要本地存在对应的镜像, 如…...
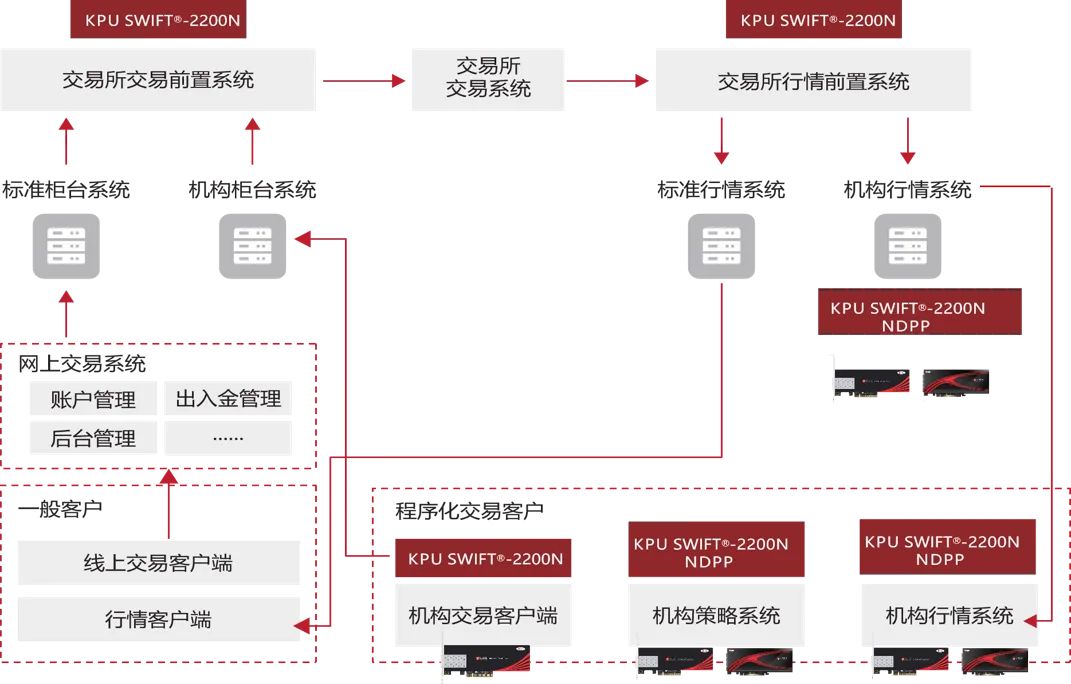
中科驭数超低时延网络解决方案入选2023年度金融信创优秀解决方案
近日,由中国人民银行领导、中国金融电子化集团有限公司牵头组建的金融信创生态实验室发布「2023年度第三期金融信创优秀解决方案」,中科驭数超低时延网络解决方案从众多方案中脱颖而出,成功入选,代表了该方案的技术创新和金融实践…...
应用方案 | DCDC电源管理芯片MC34063A
MC34063A 为一单片 DC-DC 变换集成电路,内含温度补偿的参考电压源(1.25V)、比较器、能有效限制电流及控制工作周期的振荡器,驱动器及大电流输出开关管等。外配少量元件,就能组成升压、降压及电压反转型 DC-DC 变换器。…...
【个人使用推荐】联机不卡顿 小白一键部署 大厂云服务器选购指南 16G低至26 幻兽帕鲁最大更新来袭
更新日期:4月8日(半年档 价格回调,京东云采购季持续进行) 本文纯原创,侵权必究 《最新对比表》已更新在文章头部—腾讯云文档,文章具有时效性,请以腾讯文档为准! 【腾讯文档实时更…...

57 npm run build 和 npm run serve 的差异
前言 npm run serve 和 npm run build 的差异 这里主要是从 vue-cli 的流程 来看一下 我们经常用到的这两个命令, 他到传递给 webpack 打包的时候, 的一个具体的差异, 大致是配置了那些东西? 经过了那些流程 ? vue-cli 的 vue-plugin 的加载 内置的 plugin 列表如下, 依次…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
