二分查找 -- 力扣(LeetCode)第704题
题目
https://leetcode.cn/problems/binary-search/description/
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
思路
这道题前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是 while(left < right) 还是 while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?
大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
下面我用这两种区间的定义分别讲解两种不同的二分写法。

二分法 第一种写法
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:

代码如下:(详细注释)(C++)
// 版本一
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2if (nums[middle] > target) {right = middle - 1; // target 在左区间,所以[left, middle - 1]} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,所以[middle + 1, right]} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};- 时间复杂度:O(log n)
- 空间复杂度:O(1)
二分法第二种写法
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
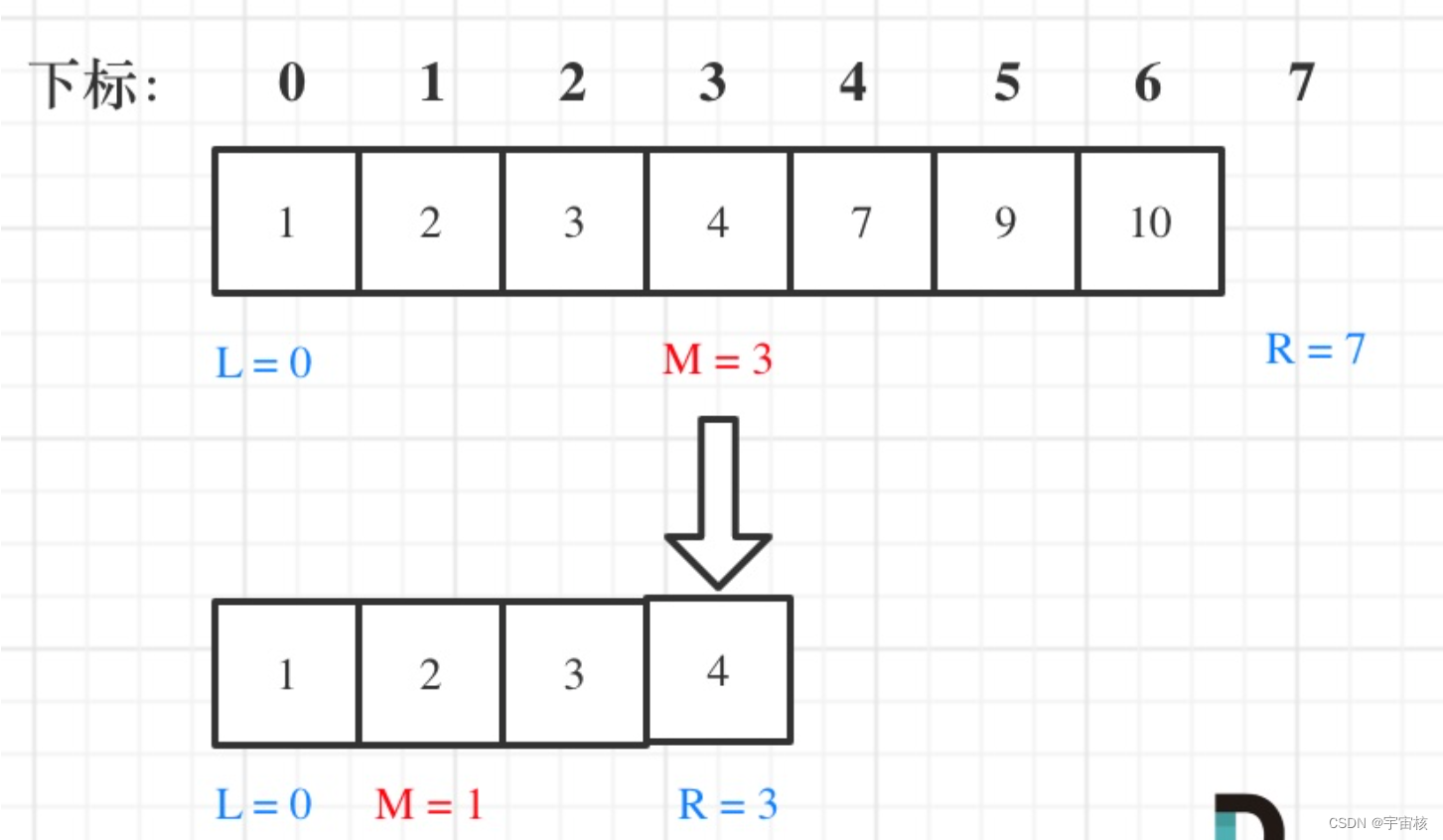
代码如下:(详细注释)(C++)
// 版本二
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <int middle = left + ((right - left) >> 1);if (nums[middle] > target) {right = middle; // target 在左区间,在[left, middle)中} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,在[middle + 1, right)中} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};- 时间复杂度:O(log n)
- 空间复杂度:O(1)
总结
二分法是非常重要的基础算法,为什么很多同学对于二分法都是一看就会,一写就废?
其实主要就是对区间的定义没有理解清楚,在循环中没有始终坚持根据查找区间的定义来做边界处理。
区间的定义就是不变量,那么在循环中坚持根据查找区间的定义来做边界处理,就是循环不变量规则。
本篇根据两种常见的区间定义,给出了两种二分法的写法,每一个边界为什么这么处理,都根据区间的定义做了详细介绍。
相信看完本篇应该对二分法有更深刻的理解了。
注意
在下面的代码中,使用 middle = left + (right - left) / 2 而不是 middle = (left + right) / 2 的主要原因是为了防止整数溢出。
当 left 和 right 都很大且接近 int 类型的最大值时,它们的和可能会超出 int 类型能够表示的范围,从而导致溢出。溢出后的结果再除以2,可能会导致一个不正确的中间索引值。
为了避免这种溢出情况,我们计算 right - left,这个差值一定小于或等于 right,然后再加到 left 上。这样即使 right 很大,right - left 仍然是一个可以安全处理的整数,再与 left 相加,并进行整数除法,就可以得到一个正确的中间索引,而不会导致溢出。
因此,虽然 middle = (left + right) / 2 在很多情况下也能正常工作,但在处理非常大的整数时,使用 middle = left + (right - left) / 2 更为稳妥和安全。这是一种常见的二分查找算法中的优化技巧,用于确保代码在极端情况下也能正确运行。
小提示
对于 middle = left + (right - left) / 2,这个表达式中的操作包括加法、减法和整数除法。在这个特定的表达式中,减法和加法具有相同的优先级,并且都是左结合的,所以它们会按照从左到右的顺序进行。整数除法 / 在这个表达式中的优先级低于加法和减法,所以加法和减法会首先进行。
其他语言版本
Java
(版本一)左闭右闭区间
class Solution {public int search(int[] nums, int target) {// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算if (target < nums[0] || target > nums[nums.length - 1]) {return -1;}int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target)return mid;else if (nums[mid] < target)left = mid + 1;else if (nums[mid] > target)right = mid - 1;}return -1;}
}(版本二)左闭右开区间
class Solution {public int search(int[] nums, int target) {int left = 0, right = nums.length;while (left < right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target)return mid;else if (nums[mid] < target)left = mid + 1;else if (nums[mid] > target)right = mid;}return -1;}
}Python
(版本一)左闭右闭区间
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里,[left, right]while left <= right:middle = left + (right - left) // 2if nums[middle] > target:right = middle - 1 # target在左区间,所以[left, middle - 1]elif nums[middle] < target:left = middle + 1 # target在右区间,所以[middle + 1, right]else:return middle # 数组中找到目标值,直接返回下标return -1 # 未找到目标值(版本二)左闭右开区间
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) # 定义target在左闭右开的区间里,即:[left, right)while left < right: # 因为left == right的时候,在[left, right)是无效的空间,所以使用 <middle = left + (right - left) // 2if nums[middle] > target:right = middle # target 在左区间,在[left, middle)中elif nums[middle] < target:left = middle + 1 # target 在右区间,在[middle + 1, right)中else:return middle # 数组中找到目标值,直接返回下标return -1 # 未找到目标值C
(版本一)左闭右闭区间
// (版本一) 左闭右闭区间 [left, right]
int search(int* nums, int numsSize, int target){int left = 0;int right = numsSize-1;int middle = 0;//若left小于等于right,说明区间中元素不为0while(left<=right) {//更新查找下标middle的值middle = (left+right)/2;//此时target可能会在[left,middle-1]区间中if(nums[middle] > target) {right = middle-1;} //此时target可能会在[middle+1,right]区间中else if(nums[middle] < target) {left = middle+1;} //当前下标元素等于target值时,返回middleelse if(nums[middle] == target){return middle;}}//若未找到target元素,返回-1return -1;
}(版本二)左闭右开区间
// (版本二) 左闭右开区间 [left, right)
int search(int* nums, int numsSize, int target){int length = numsSize;int left = 0;int right = length; //定义target在左闭右开的区间里,即:[left, right)int middle = 0;while(left < right){ // left == right时,区间[left, right)属于空集,所以用 < 避免该情况int middle = left + (right - left) / 2;if(nums[middle] < target){//target位于(middle , right) 中为保证集合区间的左闭右开性,可等价为[middle + 1,right)left = middle + 1;}else if(nums[middle] > target){//target位于[left, middle)中right = middle ;}else{ // nums[middle] == target ,找到目标值targetreturn middle;}}//未找到目标值,返回-1return -1;
}相关文章:

二分查找 -- 力扣(LeetCode)第704题
题目 https://leetcode.cn/problems/binary-search/description/ 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例…...

Windows下如何确定虚函数在虚函数表中的位置
我需要用c#调用 c 的 类的函数, 虽然可以通过头文件的顺序,但是如果可以打印出虚函数在虚表中的Offset更好。 测试要求: Windows, x86 只有1层虚函数,没有被override过 虚函数调用如下 auto a_reqCreditDetail &XtTraderApi::reqCreditDetail; (a…...
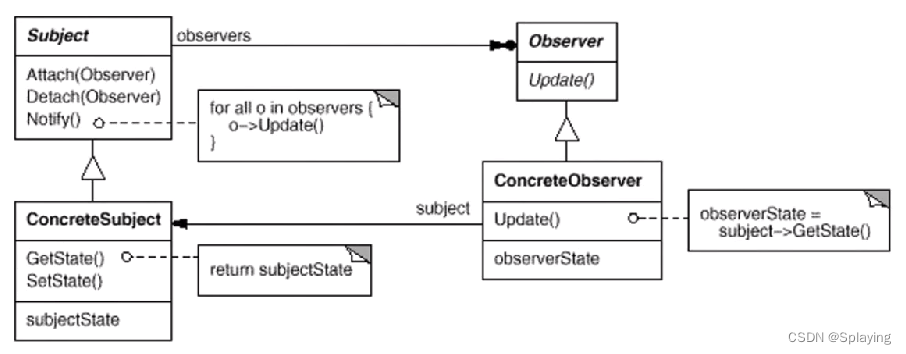
C++设计模式:观察者模式(三)
1、定义与动机 观察者模式定义:定义对象间的一种1对多(变化)的依赖关系,以便当一个对象(Subject)的状态发生比改变时,所有依赖于它的对象都得到通知并且自动更新 再软件构建过程中,…...

CentOS运行Py脚本报错illegal instruction故障处理
测试Python脚本运行环境及依赖 [root@localhost network]# python3 devops_ping_test1.py Illegal instruction ①、illegal instruction报错 由于本人第一次测试时运行是正常的,但是在测试过程中多次修改、覆盖代码运行后提示Illegal instruction(非法指令),所以不能单…...

软件设计师——1.备考提纲
知识点说明比例软件工程基础知识11开发模型、设计原则、测试方法、质量特性、CMM、Pert图、风险管理14.67%面向对象12面向对象基本概念、面向对象分析与设计、UML、设计模式16.00%数据结构与算法10数组、栈、队列、树与二叉树、图、查找与排序、常见算法13.33%程序设计语言6文法…...
[开源] 基于GRU的时间序列预测模型python代码
基于GRU的时间序列预测模型python代码分享给大家,记得点赞哦 #!/usr/bin/env python # coding: utf-8import time time_start time.time() import numpy as np import matplotlib.pyplot as plt import pandas as pd import math from keras.models import Sequent…...

SQL SERVER 备份
目录 1.备份概念 1.1 为何备份? 1.2 SQL Server 备份模式 2.SQL Server 数据库备份 2.1 借助SSMS备份数据库 2.2 借助 T-SQL 备份数据库 2.3 创建加密备份 2.4 备份文件和文件组 权限 步骤 2.5 备份事务日志 3.维护计划 3.1 完整备份 3.2 差异备份...
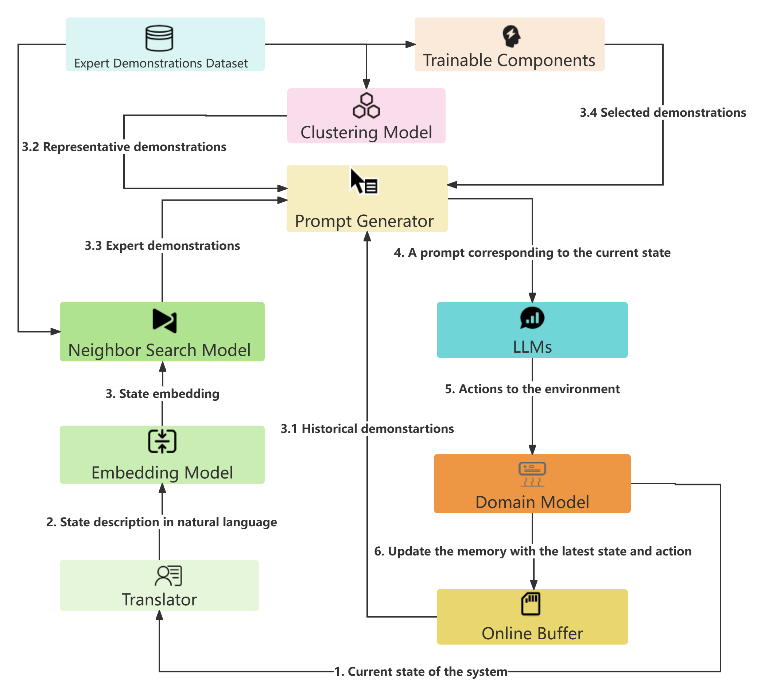
提示词专场:从调整提示改善与LLMs的沟通,到利用LLMs优化提示效果
编者按:欢迎阅读“科研上新”栏目!“科研上新”汇聚了微软亚洲研究院最新的创新成果与科研动态。在这里,你可以快速浏览研究院的亮点资讯,保持对前沿领域的敏锐嗅觉,同时也能找到先进实用的开源工具。 提示词的好坏决…...
测开面经(pytest测试案例,接口断言,多并发断言)
pytest对用户登录接口进行自动化脚本设计 a. 创建一个名为"test_login.py"的测试文件,编写以下测试脚本 import pytest import requests# 测试用例1:验证登录成功的情况 # 第一个测试用例验证登录成功的情况,发送有效的用户名和密…...

Golang 开发实战day09 - package Scope
🏆个人专栏 🤺 leetcode 🧗 Leetcode Prime 🏇 Golang20天教程 🚴♂️ Java问题收集园地 🌴 成长感悟 欢迎大家观看,不执着于追求顶峰,只享受探索过程 Golang 教程09 - package Sc…...

24考研-东南大学916经验贴
文章目录 一、个人情况二、初试备考经验1.政治 67,客观382.英语 60,客观大概40左右3.数学 136,客观应该满分4.专业课 数据结构计网 114小分不清楚 三、复试备考经验笔试:C面试复试流程 附一下成绩单: 一、个人情况 本…...

【AI面试】YOLO 如何通过 k-means 得到 anchor boxes的?Yolo、SSD 和 faster rcnn 的正负样本定义
如果你的项目中有目标检测相关的内容,那么本篇内容就一定要好好看看。不会的看到了理解下,会的看看是不是和自己理解的一样。 一、YOLO 如何通过 k-means 得到 anchor boxes的? YOLOv2 和 YOLOv3是目标检测领域中非常流行的算法,它们都使用了anchor boxes来提高检测的准确…...

MySQL高级篇(B-Tree、Btree)
目录 1、Btree(B-Tree) 1.1、B-Trees的特点 二叉树缺点:顺序插入时,会形成一个链表,查询性能大大降低。大数据量情况下,层级较深,检索速度慢。红黑树:大数据量情况下,层…...

Zookeeper脑裂解决方案
Zookeeper脑裂原因: 主要原因是Zookeeper集群和Zookeeper client判断超时并不能做到完全同步,也就是说可能一前一后,如果是集群先于client发现,那就会出现上面的情况。同时,在发现并切换后通知各个客户端也有先后快慢…...

常用日常脚本
日常脚本 1:主机初始化脚本 通用脚本: curl -s http://内网ip:3333/soft/shell/init/init_vm.sh |sh 以下是单一功能脚本 2:定时检测dns,并修改为固定dns curl -s http://内网ip:3333/soft/shell/init/deploy_dns_product.sh | s…...
Longan Pi 3H 开发板体验
Longan Pi 3H 开发板体验 开箱内容 打开包装,你可以看到以下物品 一个Longan Pi 3H盒子Longan Pi 3H开发板 产品基本介绍 Longan Pi 3H 是基于 Longan Module 3H 核心板的 ARM Linux 开发板,以 H618 (Quad core ARM Cortex-A531.5Ghz , 64-bit) 为主控…...
SpringCloud Alibaba Sentinel 创建流控规则
一、前言 接下来是开展一系列的 SpringCloud 的学习之旅,从传统的模块之间调用,一步步的升级为 SpringCloud 模块之间的调用,此篇文章为第十四篇,即介绍 SpringCloud Alibaba Sentinel 创建流控规则。 二、基本介绍 我们在 senti…...

Mysql底层原理五:如何设计、用好索引
1.索引的代价 空间上的代价 时间上的代价 每次对表中的数据进⾏增、删、改操作时,都需要去修改各个B树索引。⽽且我们讲过,B树每层节点都是按照索引列的值从⼩到⼤的顺序排序⽽组成了双 向链表。不论是叶⼦节点中的记录,还是内节点中的记录&a…...

python学习杂记
做为一个接近40岁的人,开始学习python会有什么结果?反正很迷茫,思维方式也开始下降了,希望可以学得好吧 早期做的是前端开发,java也有所接触,但是都学得不精,后来转做项目管理,把技…...

C# Socket发送、接收结构体
Socket发送:Socket的使用 一、Socket发送结构体 结构体如下: [StructLayout(LayoutKind.Sequential, Pack 1)] public struct OutPoint_ST {public int LeftheartX;public int LeftHeartY;public float WidthHeart;public int RightHeartX;public in…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
