树的基本概念与二叉树
文章目录
- 树的基本概念与二叉树
- 一、树的概念和结构
- 1. 树的概念
- 2. 树的相关概念
- 二、树的存储
- 1. 左孩子右兄弟表示法
- 2. 双亲表示法
- 三、二叉树
- 1. 特殊的二叉树
- 1.1 满二叉树
- 1.2 完全二叉树
树的基本概念与二叉树
一、树的概念和结构
1. 树的概念
树是一种非线性的数据结构,它是由 n (n≥0) 个有限结点组成一个具有层次关系的集合。之所以称之为"树",是因为它的结构看起来像一棵倒挂的树,根朝上,叶子朝下。树具有以下特点:
- 有一个特殊的节点,称为根节点,根节点没有前驱节点。
- 除根节点外,其余节点被分成 M 个 (M>0) 互不相交的集合。
- 树是递归定义的。
- 在树形结构中,子树之间不能有交集,否则就不是树形结构。
2. 树的相关概念
- 节点的度: 一个节点含有的子树的个数称为该节点的度。
- 叶节点或终端节点: 度为 0 的节点称为叶节点。
- 非终端节点或分支节点: 度不为 0 的节点。
- 双亲节点或父节点: 若一个节点含有子节点,则这个节点称为其子节点的父节点。
- 孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点。
- 兄弟节点: 具有相同父节点的节点互称为兄弟节点。
- 树的度: 一棵树中,最大的节点的度称为树的度。
- 节点的层次: 从根节点开始定义,根为第一层,根的子节点为第二层,以此类推。
- 树的高度或深度: 树中节点的最大层次。
- 堂兄弟节点: 双亲在同一层的节点互为堂兄弟。
- 节点的祖先: 从根到该节点所经分支上的所有节点。
- 子孙: 以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林: 由 m (m>0) 棵互不相交的树的集合称为森林。
需要注意的是:
- 当树为空树时,树的高度/深度通常设为 0。
- 子树之间是不能相交的。
- 除了根节点外,每个节点有且仅有一个父节点。
- 一棵拥有 N 个节点的树有 N-1 条边。
二、树的存储
1. 左孩子右兄弟表示法
左孩子右兄弟表示法是树形结构的一种常见且最优的存储方式。其结点结构如下:
struct TreeNode {int val;struct TreeNode* firstChild; // 指向最左边的第一个孩子结点struct TreeNode* nextSibling; // 指向当前节点右边一个兄弟结点
};
- firstChild: 指向最左边的第一个孩子结点,如果没有则指向 null。
- nextSibling: 指向当前节点右边的一个兄弟节点,如果没有则指向 null。
2. 双亲表示法
双亲表示法不存储指向孩子的指针,只存储指向父亲的指针或下标。
- 不支持从根找孩子,只支持从孩子找父亲。
- 判断两个节点是否在同一棵树中,可以通过寻找它们的根节点是否相同来确定。
- 并查集就是使用双亲表示法实现的。
- 根节点没有父亲,所以通常存储 -1。
三、二叉树

二叉树是一种特殊的树形结构,它实行了"计划生育",每个节点最多只能有两个孩子。二叉树具有以下特点:
- 二叉树中不存在度大于 2 的节点,每个节点最多有两个孩子,也可以只有一个孩子或没有孩子。
- 二叉树由一个根节点以及两棵分别称为左子树和右子树的二叉树组成。
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
- 二叉树有多种情况:空树、只有根节点、只有左子树、只有右子树以及左右子树都存在。
1. 特殊的二叉树
1.1 满二叉树
满二叉树是指一棵二叉树的每一层节点数都达到最大值。对于一棵高度为 h 的满二叉树,它一共有 (2^h)-1 个节点。证明如下:
设 F(h) 表示高度为 h 的满二叉树的节点总数,则有:
F(h) = 2^0 + 2^1 + 2^2 + ... + 2^(h-2) + 2^(h-1)
这是一个等比数列,其前 n 项和公式为:
Sn = (a1 * (1 - q^n)) / (1 - q)
代入 a1 = 1, q = 2, n = h,得:
F(h) = (2^h) - 1
另一种证明方法是错位相减法:
- `2F(h) = 2^1 + 2^2 + 2^3 + … + 2^(h-1) + 2^h
F(h) = 2^0 + 2^1 + 2^2 + ... + 2^(h-2) + 2^(h-1)
F(h) = 2^h - 2^0 = 2^h - 1
1.2 完全二叉树
完全二叉树是由满二叉树引出来的,其效率很高。满二叉树是完全二叉树的一种特殊情况。
假设二叉树的高度为 h,则完全二叉树满足以下条件:
- 前 h-1 层都是满的。
- 第 h 层不一定满,但第 h 层的节点从左到右是连续的。
对于高度为 h 的完全二叉树,其节点数的范围是 [2^(h-1), 2^h - 1]。
以上就是对树的基本概念以及二叉树的介绍。树是一种非常重要且常用的数据结构,在计算机科学领域有着广泛的应用。深入理解树的概念和特性,对于解决实际问题和优化算法设计都有很大帮助。
相关文章:

树的基本概念与二叉树
文章目录 树的基本概念与二叉树一、树的概念和结构1. 树的概念2. 树的相关概念 二、树的存储1. 左孩子右兄弟表示法2. 双亲表示法 三、二叉树1. 特殊的二叉树1.1 满二叉树1.2 完全二叉树 树的基本概念与二叉树 一、树的概念和结构 1. 树的概念 树是一种非线性的数据结构,它是…...

什么是物理服务器?
物理服务器又叫做独立服务器,指物理上的单独服务器,是有着实体的服务器并不是虚拟的,物理服务器也可以理解成一台超大的电脑,但是对于普通的家用电脑来说,物理服务器需要长期处于开机的状态,对于硬件性能消…...
数据结构:详解【树和二叉树】
1. 树的概念及结构(了解) 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝…...
“成像光谱遥感技术中的AI革命:ChatGPT在遥感领域中的应用“
遥感技术主要通过卫星和飞机从远处观察和测量我们的环境,是理解和监测地球物理、化学和生物系统的基石。ChatGPT是由OpenAI开发的最先进的语言模型,在理解和生成人类语言方面表现出了非凡的能力。本文重点介绍ChatGPT在遥感中的应用,人工智能…...
semhear环境sox
这里写自定义目录标题 pip list 看到当前环境下已经有sox了怀疑跟torchaudio和torchvision有关,更新了一下:装了torchvisionsox还是找不到 pip list 看到当前环境下已经有sox了 怀疑跟torchaudio和torchvision有关,更新了一下: p…...

如何快速开启一个项目-ApiHug - API design Copilot
ApiHug101-001开启篇 🤗 ApiHug {Postman|Swagger|Api...} 快↑ 准√ 省↓ GitHub - apihug/apihug.com: All abou the Apihug apihug.com: 有爱,有温度,有质量,有信任ApiHug - API design Copilot - IntelliJ IDEs Plugin |…...

从用友U9到钉钉通过接口配置打通数据
从用友U9到钉钉通过接口配置打通数据 接通系统:用友U9 用友U9cloud深耕制造领域十三载,U9cloud在机械、电子、汽配、家具、整车、军工等细分行业有着深厚的积累,尤其是机械、电子和汽配行业,不但打造了多个成熟的产品模式和应用场…...
PyQt qrc2py 使用PowerShell将qrc文件转为py文件并且将导入模块PyQt或PySide转换为qtpy模块开箱即用
前言 由于需要使用不同的qt环境(PySide,PyQt)所以写了这个脚本,使用找到的随便一个rcc命令去转换qrc文件,然后将导入模块换成qtpy这个通用库(支持pyside2-6,pyqt5-6),老版本的是Qt.py(支持pysi…...
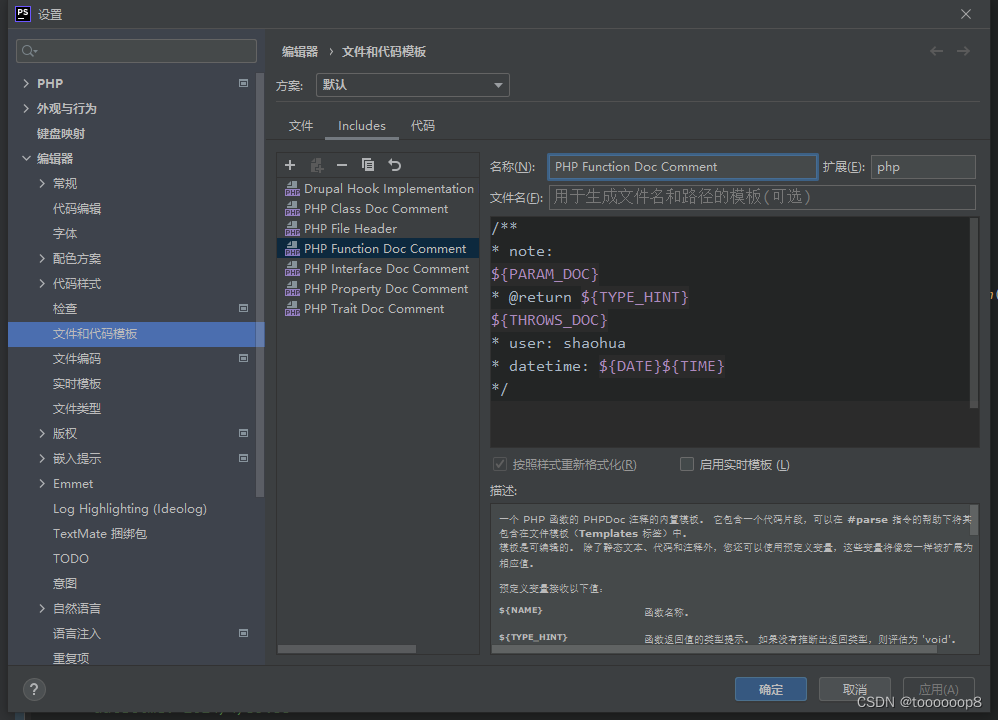
phpstorm设置头部注释和自定义注释内容
先说设置位置: PhpStorm中文件、类、函数等注释的设置在:setting-》Editor-》FIle and Code Template-》Includes-》PHP Function Doc Comment下设置即可,其中方法的默认是这样的: /** ${PARAM_DOC} #if (${TYPE_HINT} ! "…...

【数据分析面试】10. 计算平均通勤时间(SQL:timestampdiff() 和datediff()区别)
题目 假设你在Uber工作。rides表包含了关于Uber用户在美国各地的行程信息。 编写一个查询,以获取纽约(NY)每位通勤者的平均通勤时间(以分钟为单位),以及纽约所有通勤者的平均通勤时间(以分钟为…...
)
2024年150道高频Java面试题(二十二)
43. ArrayList 和 Vector 的区别是什么? ArrayList 和 Vector 是 Java 中用于存储对象的两种不同类型的动态数组。它们都实现了 List 接口,但存在一些重要的区别: 同步性: ArrayList 是不同步的,意味着它不是线程安全…...
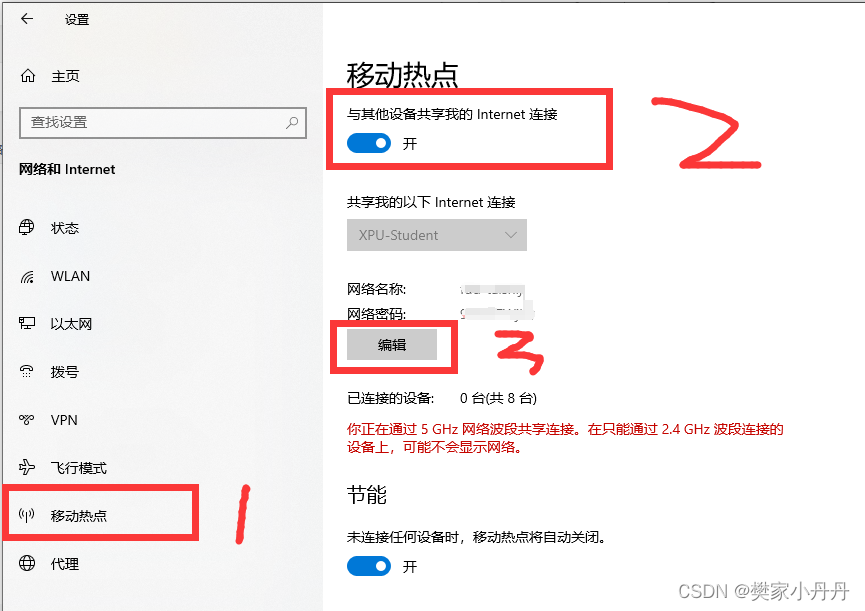
如何使用校园网——Win10笔记本,台式机互开热点
当我们使用校园网的时候,往往只能连接一个电脑端,但是又想两个机子同时连接WIFI怎么办呢? 当然,前提条件是你先得其中一台电脑有网络哈 1、打开想开共享热点的电脑的设置 A、点击WIN,再点击设置 2、点击网络和Inte…...

c#:简洁实现if-else语句
c#:简洁实现if-else语句 在C#中,可以使用三元运算符(? :)来简洁地实现if-else语句。其语法格式为: 条件表达式 ? 表达式1 : 表达式2 例如:当条件表达式为真时,返回表达式1的值,否…...
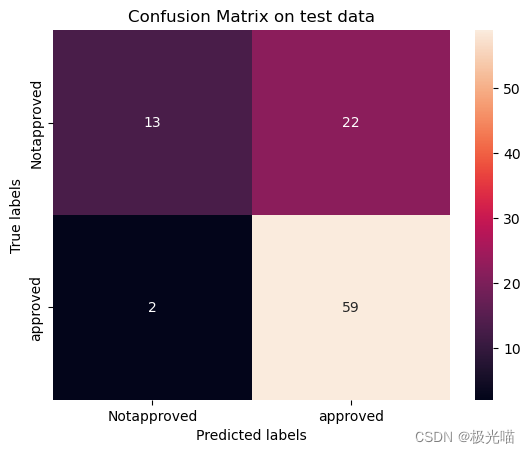
金融贷款批准预测项目
注意:本文引用自专业人工智能社区Venus AI 更多AI知识请参考原站 ([www.aideeplearning.cn]) 在金融服务行业,贷款审批是一项关键任务,它不仅关系到资金的安全,还直接影响到金融机构的运营效率和风险管理…...
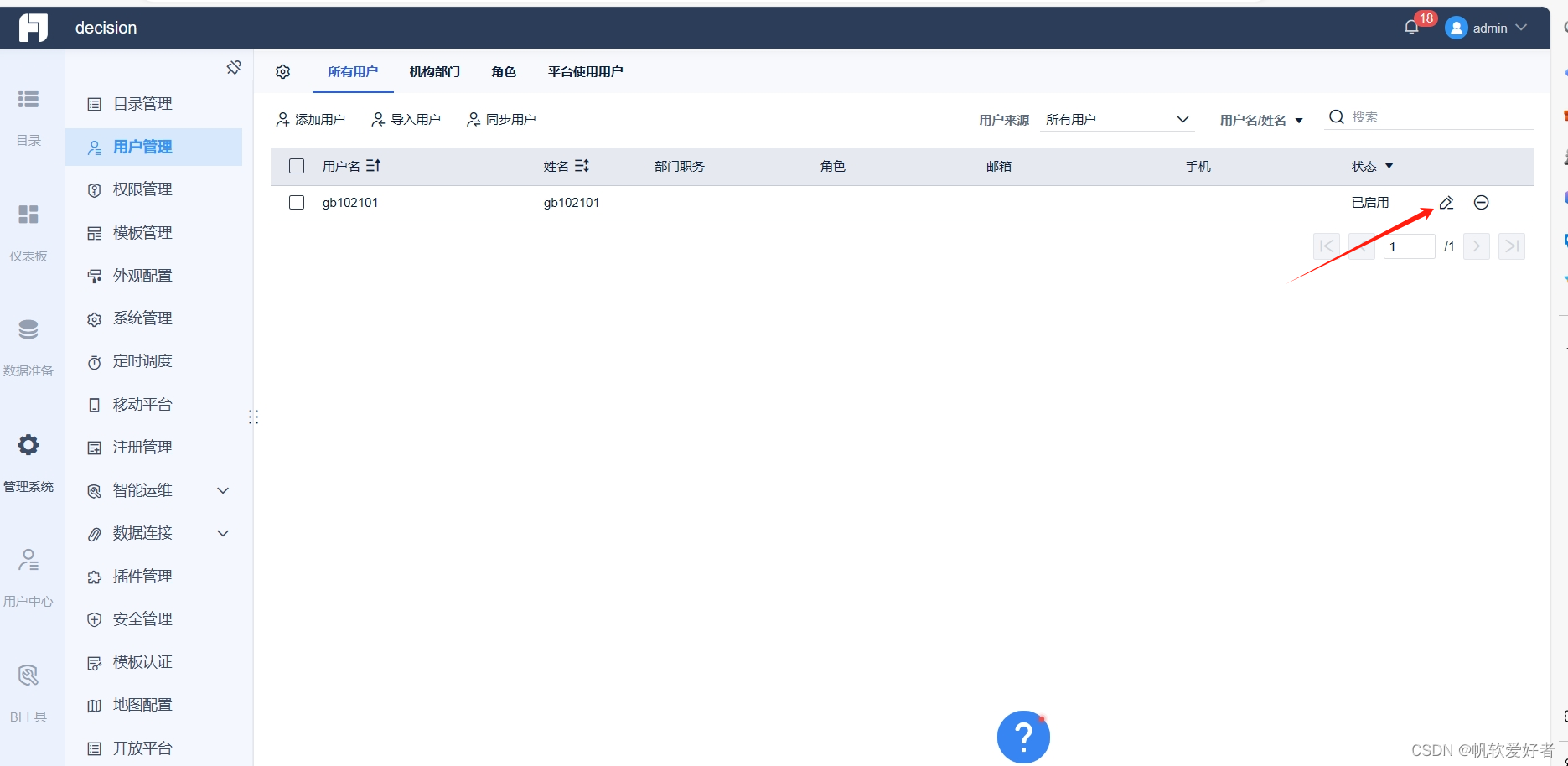
FR中隐藏系统管理--用户管理中 表格中每条数据中的编辑按钮,删除按钮
比如隐藏删除按钮: var userTableTools BI.Constants.getConstant("dec.constant.user.table.tools")for(var key in userTableTools){if(key "delete"){var deleteItem userTableTools["delete"]deleteItem.invisible true;}}...

函数重载和引用【C++】
文章目录 函数重载什么是函数重载?函数重载的作用使用函数重载的注意点为什么C可以函数重载,C语言不行? 引用什么是引用?引用的语法引用的特点引用的使用场景引用的底层实现传参时传引用和传值的效率引用和指针的区别 函数重载 什…...

rust-tokio发布考古
源头: Carl Lerche Aug 4, 2016 I’m very excited to announce a project that has been a long time in the making. 我很兴奋地宣布一个酝酿已久的项目。 Tokio is a network application framework for rapid development and highly scalable deployments…...
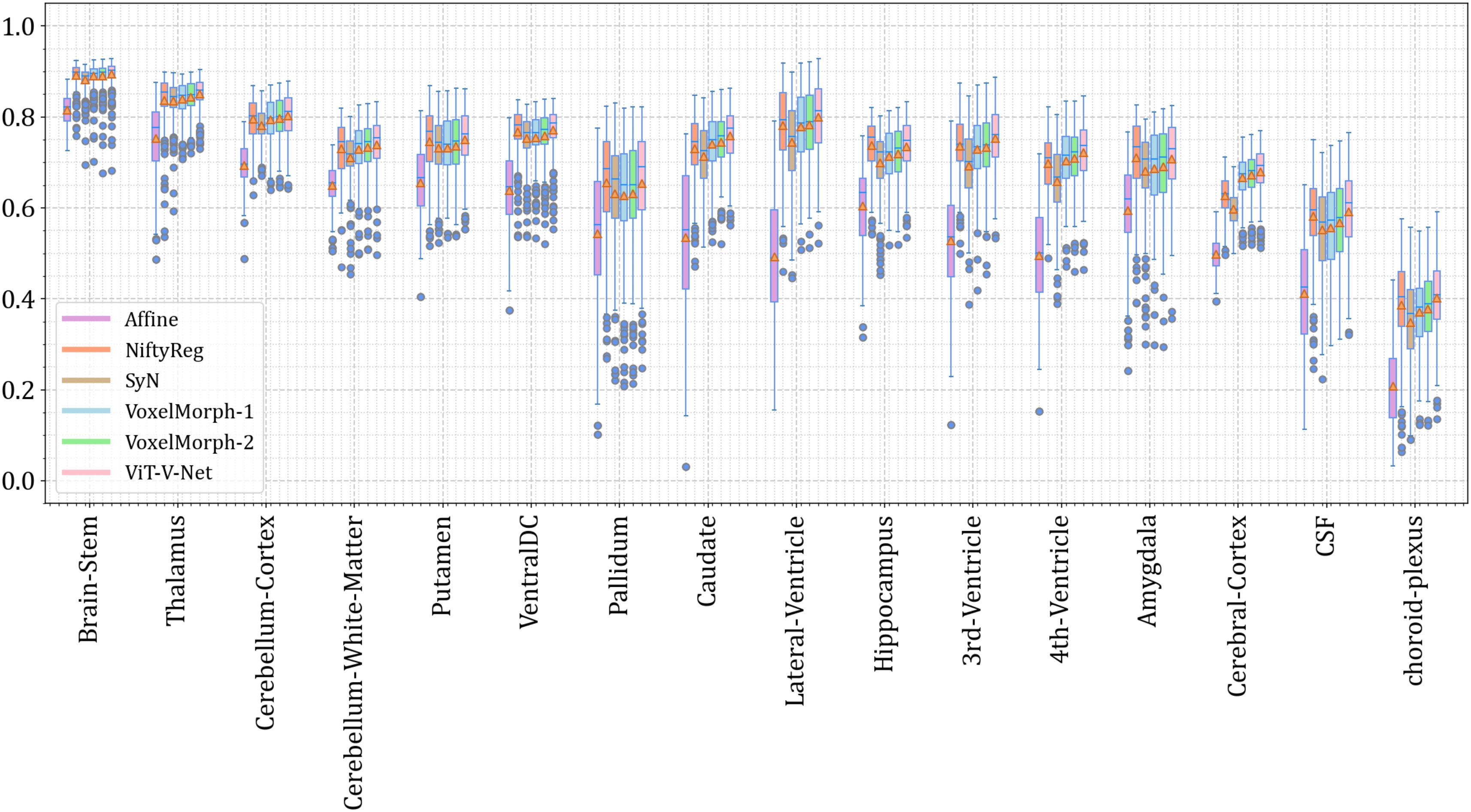
3D医疗图像配准 | 基于Vision-Transformer+Pytorch实现的3D医疗图像配准算法
项目应用场景 面向医疗图像配准场景,项目采用 Pytorch ViT 来实现,形态为 3D 医疗图像的配准。 项目效果 项目细节 > 具体参见项目 README.md (1) 模型架构 (2) Vision Transformer 架构 (3) 量化结果分析 项目获取 https://download.csdn.net/down…...
:状态模式)
设计模式(18):状态模式
核心 用于解决系统中复杂对象的状态转换以及不同状态下行为的封装问题 结构 环境类(Context): 环境类中维护一个State对象,它定义了当前的状态,并委托当前状态处理一些请求; 抽象状态类(State): 用于封装对象的一个特定状态所对应的行为&a…...

如果用大模型考公,kimi、通义千问谁能考高分?
都说大模型要超越人类了,今天就试试让kimi和通义千问做公务员考试题目,谁能考高分? 测评结果再次让人震惊! 问题提干:大小两种规格的盒装鸡蛋,大盒装23个,小盒装16个,采购员小王买了…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
