LeetCode 377——组合总和 Ⅳ
阅读目录
- 1. 题目
- 2. 解题思路
- 3. 代码实现
1. 题目

2. 解题思路
此题一看应该就是需要用到动态规划算法,假设我们以 f[d]表示总和为 d 的元素组合的个数,首先,我们遍历 nums 数组,
如果有 nums[i] < target,那么组合中第一个元素我们放置 nums[i],组合中余下元素的排列总个数也就变成了子问题 f[target - nums[i]]。
如果有 nums[i] = target,那么组合中只能放置 nums[i]这一个元素。
3. 代码实现
于是,我开始实现了第一版代码,完全就照着上面的解题思路来写,使用递归。
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {int ret = 0;for (int i = 0; i < nums.size(); ++i) {if (nums[i] < target) {ret += combinationSum4(nums, target-nums[i]);}else if (nums[i] == target) {ret += 1;}}return ret;}
};
很可惜,没有通过全部测试用例,超时了。
超出时间限制 10 / 16 个通过的测试用例
这里,计算 f[target - nums[i]]的时候有可能存在大量重复,比如,nums=[1, 2, 3, 4], target=5,第一个元素我们放置 2 时,需要计算 f(3)。然后,如果前两个元素我们都放置 1 时,也需要计算 f(3)。
所以,一个很自然的思路就是把已经计算过的 f(d)记录下来,下次遇到可以直接用。
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {static vector<int> target_ret(1001, -1);int ret = 0;for (int i = 0; i < nums.size(); ++i) {if (nums[i] < target) {int left = target - nums[i];if (target_ret[left] == -1) {target_ret[left] = combinationSum4(nums, left); }ret += target_ret[left];}else if (nums[i] == target) {ret += 1;}}return ret;}
};
于是,我定义了一个静态数组,全部初始化为 -1,计算一个 f(d) 后就把它记录下来,下次直接使用,不用再递归去调用一次函数。
但是,这次直接变成解答错误了。我把错误的用例单独拿出来测试,答案是对的。去网上一查,原来 LeetCode 会用这同一个类去测试所有的测试用例,那么我的静态数组就会受到前一个测试用例的影响,所以,答案也就是错的了,此路看来也不通!
那就只能手动递推了,因为我们最终要计算 f(target) ,而 f(target) 可能依赖于 f(target-1)、f(target-2)....f(1),所以我们就从 1 开始,一个一个往后计算 f(d) 即可。
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> target_ret(target+1, 0);for (int j = 1; j <= target; ++j) {for (int i = 0; i < nums.size(); ++i) {if (nums[i] < j) {int left = j - nums[i];target_ret[j] += target_ret[left];}else if (nums[i] == j) {target_ret[j] += 1;}}}return target_ret[target];}
};
很不幸,还是出错了,看起来是整型数超出表示范围了,一个简单的思路是把 int 换成 unsigned int,终于成功了!
Line 16: Char 35: runtime error: signed integer overflow: 2147483647 + 1 cannot be represented in type ‘int’ (solution.cpp)
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:25:35
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<unsigned int> target_ret(target+1, 0);for (int j = 1; j <= target; ++j) {for (int i = 0; i < nums.size(); ++i) {if (nums[i] < j) {int left = j - nums[i];target_ret[j] += target_ret[left];}else if (nums[i] == j) {target_ret[j] += 1;}}}return target_ret[target];}
};
要细究为什么会越界的话,其实题目描述里特别说明了 :
题目数据保证答案符合 32 位整数范围。
但是这里只是说 f(target) 不会越界,我们从 1 遍历到 target 的某个中间变量可能越界了,然后这个中间变量实际上是用不到的。
比如,nums=[2, 6, 9], target=15, f(14) 是不会用到的,但是我们也会计算它。
时间复杂度为 O ( t a r g e t ∗ n u m s . s i z e ( ) ) O(target*nums.size()) O(target∗nums.size()),空间复杂度为 O ( t a r g e t ) O(target) O(target)。
如果数组中存在负数的话,会存在一个包含正数和负数的序列,它们的和为 0,也就是说,可以无限添加这个序列,而和保持不变,这样,f(target) 就是无穷的了。
相关文章:

LeetCode 377——组合总和 Ⅳ
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 此题一看应该就是需要用到动态规划算法,假设我们以 f[d]表示总和为 d 的元素组合的个数,首先,我们遍历 nums 数组, 如果有 nums[i] < target,那么组…...

ubuntu同步网络时间
安装ntpdate sudo apt-get update sudo apt-get install ntpdate设置系统时间与网络时间同步 sudo ntpdate cn.pool.ntp.org设置时区亚洲上海 sudo cp /usr/share/zoneinfo/Asia/Shanghai /etc/localtime设置时间为24小时制 echo "LC_TIMEen_DK.UTF-8" >>/…...
Flink学习(四)-数据管道 ETL
一、状态转换 map() 只适用于一对一的转换,即对每个进入算子的流元素,map() 将仅输出一个转换后的元素。 flatmap() 可以输出任意数量的元素,也可以一个都不发。 二、Keyed Streams keyBy() 相当于 sql 中的 group by,通过…...
Python可视化之Matplotlib
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1、解决坐标轴刻度负号乱码2、解决中文乱码问题3、图形展现形式 一、图形绘制1.折线图plot2.散点图plot&scatter3.柱状图plt.bar&条形图plt.barh4.直方…...
ChatGPT全方位解析:如何培养 AI 智能对话技能?
简介 ChatGPT 的主要优点之一是它能够理解和响应自然语言输入。在日常生活中,沟通本来就是很重要的一门课程,沟通的过程中表达的越清晰,给到的信息越多,那么沟通就越顺畅。 和 ChatGPT 沟通也是同样的道理,如果想要C…...

[C++/Linux] UDP编程
一. UDP函数 UDP(用户数据报协议,User Datagram Protocol)是一种无连接的网络协议,用于在互联网上交换数据。它允许应用程序发送数据报给另一端的应用程序,但不保证数据报能成功到达,也就是说,它…...

深入探索Linux的lsof命令
在Linux系统中,了解哪些文件被哪些进程打开对于系统管理和问题诊断是极其重要的。这正是lsof命令,即List Open Files,发挥其强大功能的场景。本文旨在详细介绍lsof的起源、底层原理、参数意义,常见用法,并详解其返回结…...

flowable 想改变正在运行的任务,实例版本为最新,需要改哪些表
在Flowable中,要改变正在运行的任务,你需要更新相关的流程定义,具体来说,可能涉及到以下几张表: ACT_RU_TASK(运行时任务):这张表包含了当前正在运行的任务信息。你可能需要更新该表…...

统计各位数字都不同的数字个数 II
3032. 统计各位数字都不同的数字个数 II 给你两个 正整数 a 和 b ,返回 闭区间 [a, b] 内各位数字都不同的数字个数。 示例 1: 输入:a 1, b 20 输出:19 解释:除 11 以外,区间 [1, 20] 内的所有数字的各…...
Taro框架中的H5 模板基本搭建
1.H5 模板框架的搭建 一个h5 的基本框架的搭建 基础template 阿乐/H5 Taro 的基础模板...

gitea详细介绍
Gitea 是一个轻量级、易于安装的 Git 服务,提供了类似于 GitHub 的功能,如代码托管、问题追踪、团队合作等。它使用 Go 语言开发,可以在自己的服务器上进行部署,从而实现自托管的 Git 服务。Gitea 具有用户友好的界面,…...

应用性能分析系统SkyWalking的安装及使用详解
1. 前言 本文全面介绍了Skywalking的功能特点、安装步骤以及使用方法。首先,文章详细阐述了Skywalking作为一款开源的应用性能管理系统(APM)的核心功能,包括分布式追踪、服务网格观测分析、度量聚合和可视化一体化等。接着,文章提供了Skywalking的详细安装指南,包括环境…...
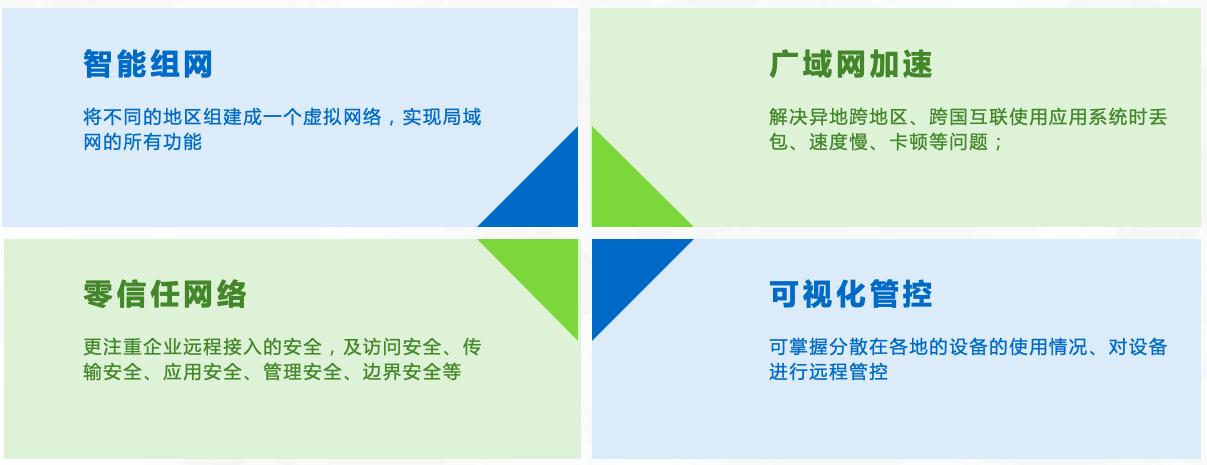
服务器远程桌面连接不上怎么办?
随着互联网的发展和远程办公的兴起,服务器远程桌面连接成为了许多企业和个人不可或缺的工具。偶尔我们可能会碰到服务器远程桌面连接不上的情况,这时候我们需要找到解决办法,确保高效地远程访问服务器。 天联组网——突破远程连接障碍 在我们…...
之适配器(bind等)整理)
C++之STL的algorithm(8)之适配器(bind等)整理
C之STL的algorithm(8)之适配器(bind等)整理 注:整理一些突然学到的C知识,随时mark一下 例如:忘记的关键字用法,新关键字,新数据结构 C 的适配器整理 C之STL的algorithm&…...

部分国企笔试总结
2024.3.30相城区某国企笔试 客观题,30分 类似考公行测题(大部分)部分计算机专业基础知识(仅几题) 主观题,70分 网络安全类一道C编程题:用户输入圆半径r,程序计算面积和周长并输出…...
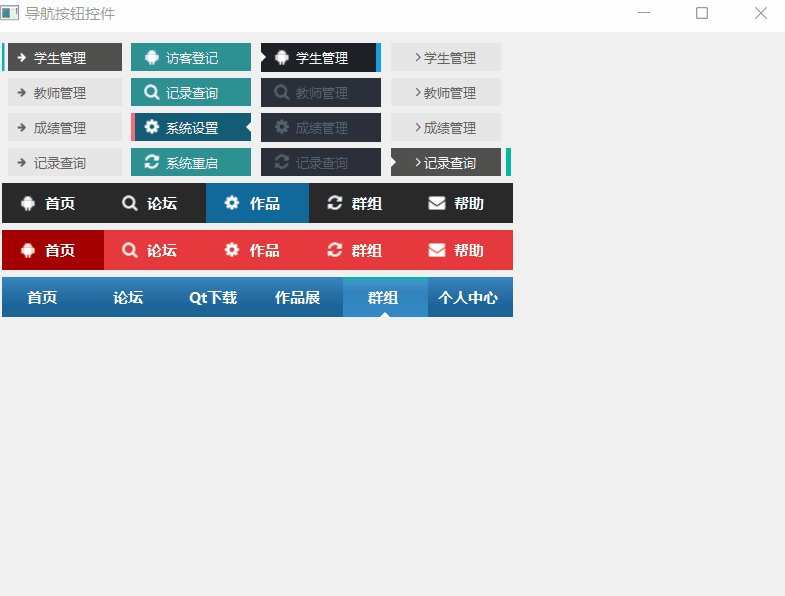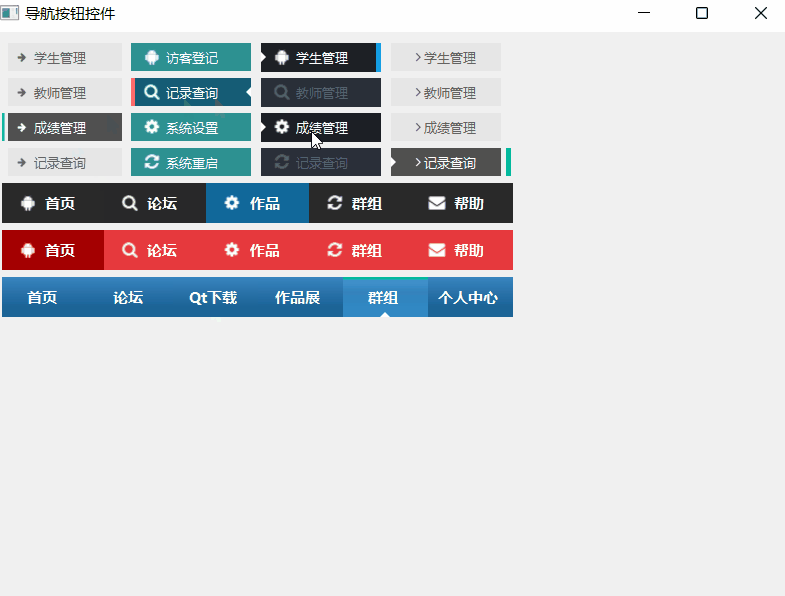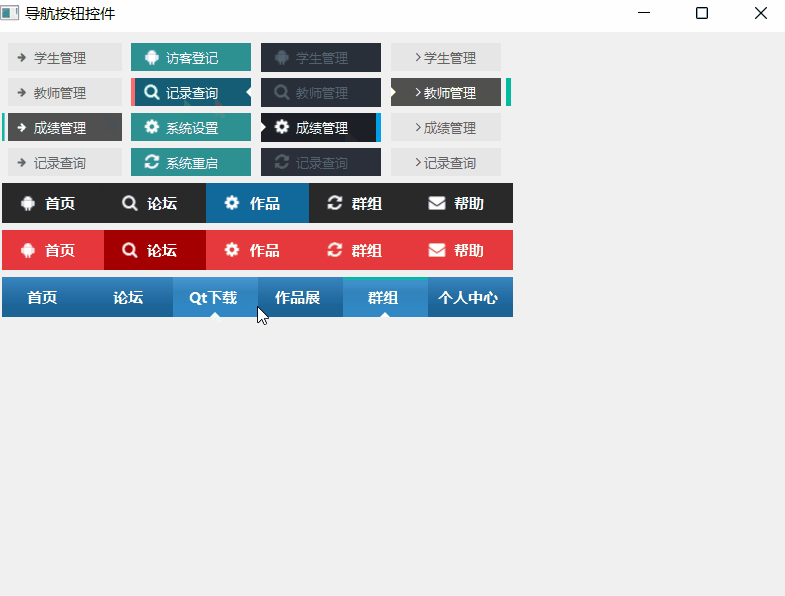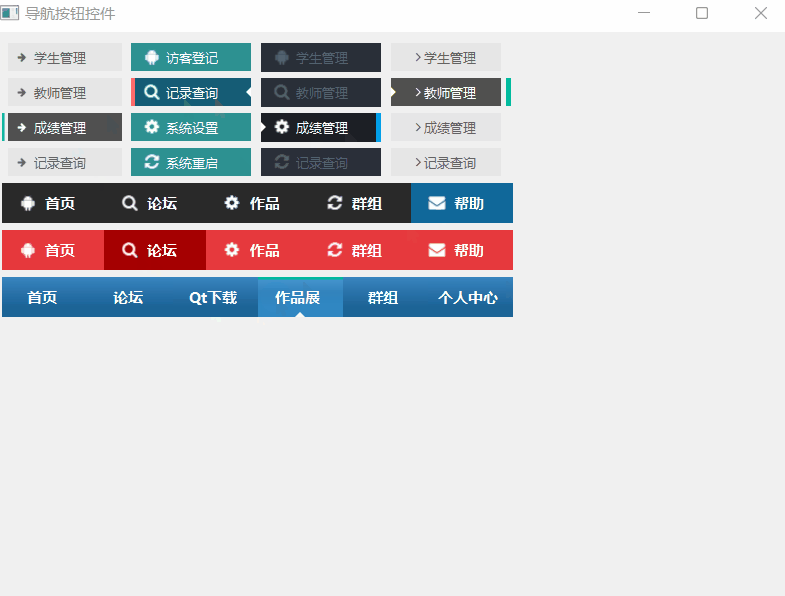
《QT实用小工具·二十二》多种样式导航按钮控件
1、概述 源码放在文章末尾 该项目实现了多种样式的导航按钮控件 可设置文字的左侧、右侧、顶部、底部间隔。 可设置文字对齐方式。 可设置显示倒三角、倒三角边长、倒三角位置、倒三角颜色。 可设置显示图标、图标间隔、图标尺寸、正常状态图标、悬停状态图标、选中状态图标…...

不定长顺序表
一.不定长顺序表的结构: typedef struct DSQList{ int* elem;//动态内存的地址 int length;//有效数据的个数 int listsize;//总容量 }DSQList,*DPSQList; 很明显,为了能实现扩容(否则如何实现再次判满呢?),我们必须要在定长顺序表的基础上增加一个总容量;结构示意图如下: 二…...

5.网络编程-socker(golang版)
目录 一、什么是socket? 二、Golang中使用TCP TCP服务端 TCP客户端 三、TCP黏包,拆包 1.什么是粘包,拆包? 2.为什么UDP没有粘包,拆包? 3.粘包拆包发生场景 4.TCP黏包 黏包服务端 …...

网格矢量如何计算莫兰指数
网格矢量如何计算莫兰指数 引言 遇到一个问题,计算矢量网格的莫兰指数。 概念解释 莫兰指数 莫兰指数(Moran’s Index)是一种空间自相关指标,用于衡量空间数据的相似性和聚集程度。它可以用来描述一个区域与其邻近区域之间的属…...

《containerd原理剖析与实战》大模型时代下如何学习云原生
大模型与云原生 近年来,大语言模型的热度可谓是愈发高涨,尤其是今年年初 Sora 的出现,更是让全球再次看到了AIGC 的巨大威力。 Sora 生成实例视频---几头巨大的长毛猛犸踏着积雪的草地而来 在当前大模型流行的时代下,云原生技术…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
