Java多路查找树(含面试大厂题和源码)
多路查找树(Multiway Search Tree),也称为B树或B+树,是一种自平衡的树形数据结构,用于存储大量数据,通常用于数据库和文件系统中。它允许在查找、插入和删除操作中保持数据的有序性,同时优化了磁盘I/O性能。
多路查找树的特点:
- 节点多个子节点:与二叉查找树不同,多路查找树的每个节点可以有多个子节点(超过两个)。
- 有序节点值:节点内部的值是有序的,通常按照升序或降序排列。
- 平衡树:树保持平衡,即所有叶子节点在同一层,或者只差一层。
- 分裂与合并操作:在插入或删除节点时,如果节点的子节点数量超过了预设的最大值,会进行节点分裂或合并操作,以保持树的平衡。
- 分层索引:多路查找树可以构建分层索引,顶层的节点包含指向下一层节点的指针,这样可以快速定位到数据所在的区域。
多路查找树的应用:
- 数据库索引:多路查找树是许多数据库系统底层实现索引结构的基础,如B树和B+树。
- 文件系统:在文件系统中,多路查找树可以用于跟踪文件的位置,优化文件的读取和写入操作。
- 内存管理:在操作系统中,多路查找树可以用于管理内存的分配和回收。
多路查找树的Java实现(简单示例):
由于多路查找树的实现相对复杂,以下是一个简化版的多路查找树的插入操作的Java代码示例:
class MultiwayNode {int key;MultiwayNode[] children;boolean isLeaf;public MultiwayNode(int key) {this.key = key;this.isLeaf = true;this.children = new MultiwayNode[2 * order - 1]; // 假设order为树的阶数}
}class MultiwaySearchTree {private MultiwayNode root;private int order; // 树的阶数public MultiwaySearchTree(int order) {this.order = order;}public void insert(int key) {root = insertRec(root, key);}private MultiwayNode insertRec(MultiwayNode node, int key) {if (node == null) {return new MultiwayNode(key);}int i = 0;for (; i < node.children.length - 1; i++) {if (key < node.children[i].key) {break;}}if (node.children[i] == null) {node.children[i] = new MultiwayNode(key);return node;} else if (i < node.children.length - 1 && !node.children[i].isLeaf) {node.children[i] = insertRec(node.children[i], key);return node;} else {// 需要分裂节点MultiwayNode newNode = splitNode(node, i);return fuseNodes(node, newNode);}}private MultiwayNode splitNode(MultiwayNode node, int index) {// 实现节点分裂逻辑// ...return new MultiwayNode(node.children[index].key);}private MultiwayNode fuseNodes(MultiwayNode node1, MultiwayNode node2) {// 实现节点合并逻辑// ...return new MultiwayNode(node1.key);}
}// 使用示例
public class Main {public static void main(String[] args) {MultiwaySearchTree tree = new MultiwaySearchTree(3); // 假设树的阶数为3tree.insert(5);tree.insert(3);tree.insert(7);tree.insert(1);tree.insert(9);// 树的结构现在应该是平衡的}
}
在实际应用中,多路查找树的实现会更加复杂,包括处理节点分裂和合并的详细逻辑,以及维护树的平衡性。在面试中,了解多路查找树的基本概念和操作是非常重要的,它展示了你对数据结构和算法的深入理解。希望这些知识点和示例代码能够帮助你更好地准备面试!
题目 1:实现一个B树的插入操作
描述:
实现一个B树的插入操作,B树是一种自平衡的多路查找树,用于维护排序的数据。给定一个B树和一个新的键值,将该键值插入到B树中,并保持树的平衡。
示例:
假设B树的阶数为3,给定一个空的B树和键值[1, 2, 3, 4, 5, 6, 7],依次插入这些键值。
Java 源码:
class BTreeNode {int key;BTreeNode[] children;boolean isLeaf;public BTreeNode(int key) {this.key = key;this.isLeaf = true;}
}class BTree {private int order;private BTreeNode root;public BTree(int order) {this.order = order;}public void insert(int key) {if (root == null) {root = new BTreeNode(key);return;}root = insertNonFull(root, key);}private BTreeNode insertNonFull(BTreeNode node, int key) {if (node.isLeaf) {int i = 0;while (i < node.children.length - 1 && key > node.children[i].key) {i++;}if (i < node.children.length) {BTreeNode newNode = new BTreeNode(key);node.children[i] = newNode;return node;}// Split the node and return the new rootreturn splitChild(node, i);} else {int i = 0;while (i < node.children.length && key < node.children[i].key) {i++;}if (i < node.children.length - 1 && !node.children[i].isLeaf) {node.children[i] = insertNonFull(node.children[i], key);} else {// Split the child node and update the parentnode.children[i] = splitChild(node.children[i], i);}}return balance(node);}private BTreeNode splitChild(BTreeNode child, int index) {int newKeys = (child.key > order / 2) ? order / 2 + 1 : order / 2;BTreeNode newChild = new BTreeNode(child.key[newKeys]);System.arraycopy(child.key, index + 1, newChild.key, 0, newKeys);child.key = Arrays.copyOfRange(child.key, 0, index + 1);child.key[newKeys - 1] = child.key[newKeys];child.key = Arrays.copyOf(child.key, newKeys);newChild.isLeaf = child.isLeaf;child.children = Arrays.copyOfRange(child.children, 0, index);child.children[newKeys - 1] = newChild;child.children = Arrays.copyOf(child.children, newKeys);return child;}private BTreeNode balance(BTreeNode node) {// Implement balancing logic if needed// ...return node;}
}// 使用示例
public class Main {public static void main(String[] args) {BTree tree = new BTree(3); // 假设B树的阶数为3for (int i = 1; i <= 7; i++) {tree.insert(i);}// B树现在应该包含所有插入的键值,并且保持平衡}
}
题目 2:实现一个B+树的查找操作
描述:
实现一个B+树的查找操作,B+树是一种特殊的多路平衡查找树,所有的数据都存储在叶子节点中。给定一个B+树和一个键值,查找该键值是否存在于B+树中。
示例:
假设B+树的阶数为4,给定一个B+树和键值[10, 20, 30, 40, 50, 60, 70],查找键值30是否存在。
Java 源码:
class BPlusLeafNode {int[] keys;BPlusLeafNode next;public BPlusLeafNode(int[] keys) {this.keys = keys;}
}class BPlusNode {BPlusNode[] children;int[] keys;boolean isLeaf;public BPlusNode(int[] keys) {this.keys = keys;this.isLeaf = keys.length == 1;}
}class BPlusTree {private BPlusNode root;private int order;public BPlusTree(int order) {this.order = order;root = new BPlusNode(new int[]{});}public boolean search(int key) {return search(root, key);}private boolean search(BPlusNode node, int key) {if (node.isLeaf) {int i = 0;while (i < node.keys.length && key > node.keys[i]) {i++;}if (i < node.keys.length && node.keys[i] == key) {return true;}return false;} else {int i = 0;while (i < node.keys.length && key < node.keys[i]) {i++;}if (i < node.keys.length) {return search(node.children[i], key);}return search(node.children[node.children.length - 1], key);}}
}// 使用示例
public class Main {public static void main(String[] args) {BPlusTree tree = new BPlusTree(4);// 假设树已经通过插入操作构建好了boolean found = tree.search(30);System.out.println("Key 30 found: " + found);}
}
题目 3:实现一个B+树的范围查询操作
描述:
实现一个B+树的范围查询操作,查询给定范围内的所有键值。B+树的所有数据都存储在叶子节点中,叶子节点之间通过指针相互连接。
示例:
假设B+树的阶数为4,给定一个B+树和键值[10, 20, 30, 40, 50, 60, 70],查询范围在[20, 50]之间的所有键值。
Java 源码:
public class BPlusTreeRangeSearch {private BPlusLeafNode findFirstLeaf(BPlusNode node, int start) {while (!node.isLeaf) {node = node.children[findFirstKeyIndex(node, start)];}return (BPlusLeafNode) node;}private int findFirstKeyIndex(BPlusNode node, int start) {int i = 0;while (i < node.keys.length - 1 && start > node.keys[i]) {i++;}return i;}public List<Integer> rangeSearch(BPlusNode root, int start, int end) {List<Integer> results = new ArrayList<>();BPlusLeafNode leaf = findFirstLeaf(root, start);if (leaf.keys[0] >= start) {int i = 0;while (leaf != null && i < leaf.keys.length && leaf.keys[i] >= start) {while (leaf.keys[i] <= end) {results.add(leaf.keys[i]);i++;}if (leaf.next != null) {leaf = leaf.next;i = 0;} else {break;}}}return results;}
}// 使用示例
public class Main {public static void main(String[] args) {BPlusTree tree = new BPlusTree(4);// 假设树已经通过插入操作构建好了BPlusTreeRangeSearch search = new BPlusTreeRangeSearch();List<Integer> results = search.rangeSearch(tree.root, 20, 50);System.out.println("Range search results: " + results);}
}
这些题目和源码展示了多路查找树在数据结构和算法问题中的应用。在面试中,能够根据问题的特点选择合适的算法并实现其解决方案是非常重要的。希望这些示例能够帮助你更好地准备面试!
相关文章:
)
Java多路查找树(含面试大厂题和源码)
多路查找树(Multiway Search Tree),也称为B树或B树,是一种自平衡的树形数据结构,用于存储大量数据,通常用于数据库和文件系统中。它允许在查找、插入和删除操作中保持数据的有序性,同时优化了磁…...

day6 | 哈希表 part-2 | 454 四数相加II 、383. 赎金信、15. 三数之和、18. 四数之和
今日任务 454 四数相加II (题目: . - 力扣(LeetCode))383 赎金信 (题目: . - 力扣(LeetCode)) 454 四数相加II 题目:. - 力扣(LeetCode) 给你四个整数数组 nums1、num…...
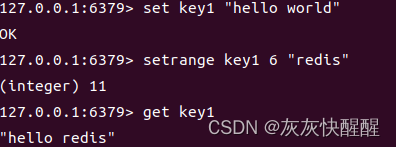
Redis常见数据类型(2)
目录 String字符串 常见命令 SET GET MGET MSET SETNX 计数命令 INCR INCRBY DECR DECRBY INCRFLOAT 其它命令 APPEND GETRANGE SETRANGE STRLEN String字符串 字符串是Redis最基础的数据类型, 关于字符串需要特别注意: (1)首先Redis中所有的键的类型都是字符…...

SparkBug解决:Type mismatch; found : org.apache.spark.sql.Column required: Double
def assginFlag(aizmuth:Double):Option[Int] {val interval 0.5val index (aizmuth / interval ).toIntif (index > 0 && index < 720 ) Some(index 1) else None} assginFlag方法中的条件判断条件 (index > 0 && index < 720) 返回的是一个布…...

MQ之————如何保证消息的可靠性
MQ之保证消息的可靠性 1.消费端消息可靠性保证: 1.1 消息确认(Acknowledgements): 消费者在接收到消息后,默认情况下RabbitMQ会自动确认消息(autoAcktrue)。为保证消息可靠性,可以…...
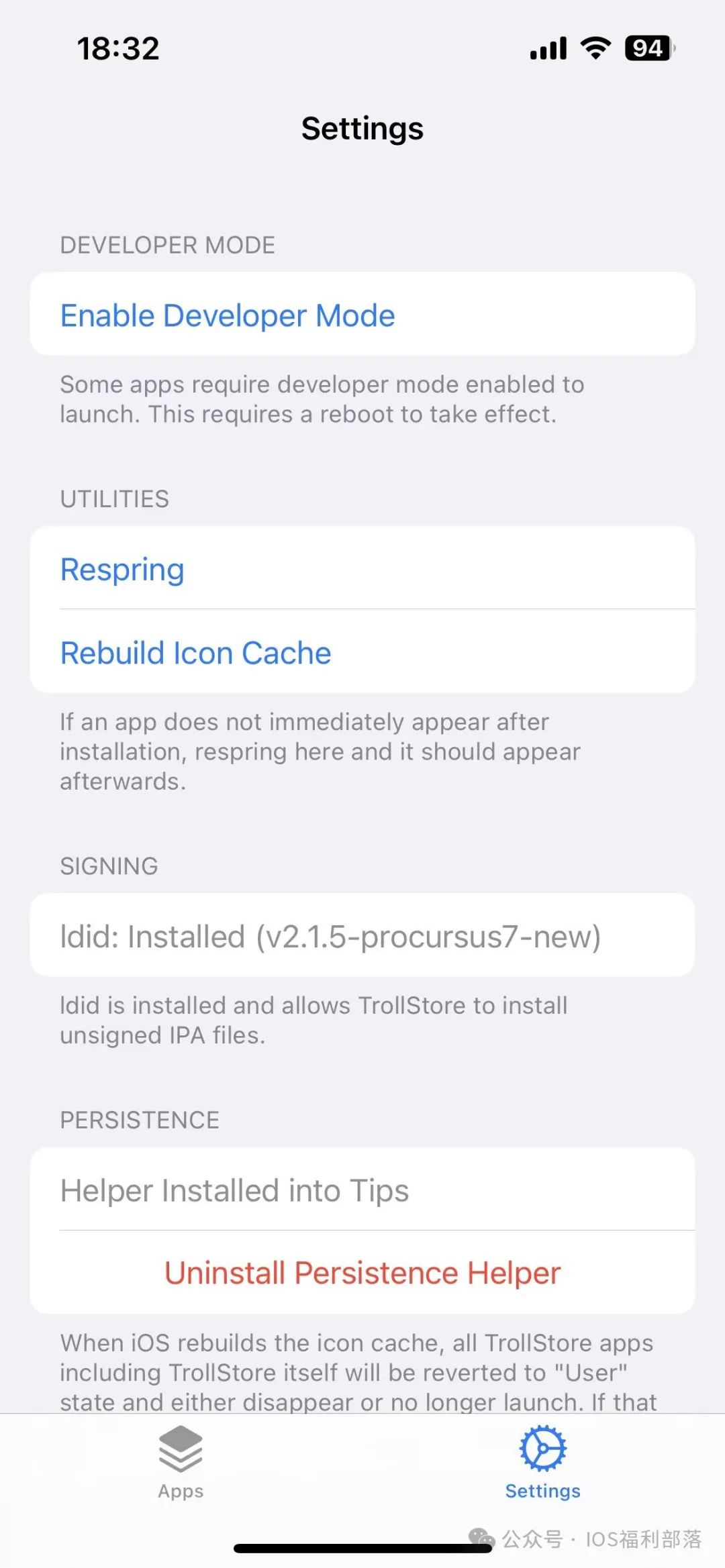
TrollInstallerX官方一键安装巨魔商店
TrollInstallerX是巨魔官方开发的一款一键巨魔商店安装器,完美支持iOS 14.0 – 16.6.1的设备,操作非常简单,TrollInstallerX依然有个小小的限制,部分机型,还是要采用间接安装方法。 一,直接安装方法 通过…...
生成随机图片验证码
随着互联网的不断发展,安全性问题日益突出。为了保障用户账号的安全性,很多网站都引入了验证码机制。验证码是一种区分用户是计算机还是人的公共全自动程序,可以有效防止恶意攻击和自动化脚本的滥用。本文将介绍如何使用Python生成随机图片验…...

【0280】《数据库系统概论》阅读总结(附xmind思维导图)
0. 阅读进展 选择性地读取了《数据库系统概论》一书中的第13、14章节,并对这两章节中较为重点的内容作了总结和归纳;然后以xmind导图形式给出。 1. xmind思维导图 Xmind附件:...
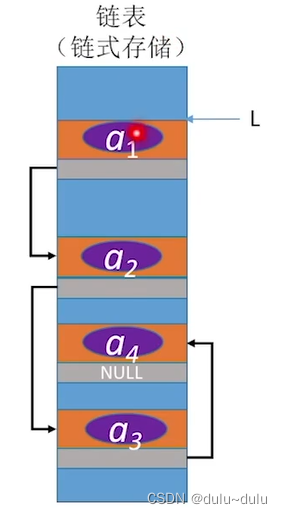
数据结构(二)----线性表(顺序表,链表)
目录 1.线性表的概念 2.线性表的基本操作 3.存储线性表的方式 (1)顺序表 •顺序表的概念 •顺序表的实现 静态分配: 动态分配: 顺序表的插入: 顺序表的删除: 顺序表的按位查找: 顺序…...

为什么你选择成为一名程序员?
文章目录 ✍选择成为程序员:兴趣与职业发展的交汇💎1 兴趣的驱动💎2 职业发展的需求💎3 结语 ✍选择成为程序员:兴趣与职业发展的交汇 在当今数字化时代,程序员已经成为一个备受瞩目的职业。无论是因为对技…...

【Android】系统启动流程分析 —— SystemServer 处理过程
本文基于 Android 14.0.0_r2 的系统启动流程分析。 SystemServer 进程主要用于创建系统服务,我们熟知的 AMS、WMS 和 PMS 都是由它来创建的,因此掌握 SystemServer 进程是如何启动的,它在启动时做了哪些工作是十分必要的。 一、源码解析 Zyg…...

Web前端—属性描述符
属性描述符 假设有一个对象obj var obj {a:1 }观察这个对象,我们如何来描述属性a: 值为1可以重写可以遍历 我们可以通过Object.getOwnPropertyDescriptor得到它的属性描述符 var desc Object.getOwnPropertyDescriptor(obj, a); console.log(desc);我…...

SpringBoot及其特性
0.前言 Spring 框架提供了很多现成的功能。那么什么是 Spring Boot?使用 Spring 框架,我们可以避免编写基础框架并快速开发应用程序。为了让 Spring 框架提供基础框架,我们需要向 Spring 框架描述有关我们的应用程序及其组件的信息。 不只是…...
「JavaEE」初识进程
初识进程 🍉进程🍌操作系统的进程管理 🍉PCB 重要属性🍌进程的身份标识🍌内存指针🍌文件描述符表🍌进程的状态🍌优先级🍌记账信息🍌上下文 🍉内存…...

计算机视觉——图像特征提取D2D先描述后检测特征提取算法原理
概述 局部特征提取是计算机视觉中的一个重要任务,它旨在从图像中提取出能够代表图像局部结构和外观信息的特征。这些特征通常用于图像匹配、物体识别、三维重建、跟踪和许多其他应用。传统方法,如尺度不变特征变换(SIFT)…...

The “from“ argument must be of type string. Received undefined——vue报错记录
今天在用机器人打包测试环境时,一直报错: The "from" argument must be of type string. Received undefined 啥意思呐? 百度也没有找到对应的问题所在。 下面写一下我的解决方法: vue.config.js 在vue.config.js中…...
汽车4S行业的信息化特点与BI建设挑战
汽车行业也是一个非常大的行业,上下游非常广,像主机厂,上游的零配件,下游的汽车流通,汽车流通之后的汽车后市场,整个链条比较长。今天主要讲的是汽车流通,汽车4S集团。一个汽车4S集团下面授权代…...

JSX 和 HTML 之间的区别
JSX和 HTML 都是用于创建和构建网页的标记语言,但它们有一些关键的区别。 1. JSX 是 JavaScript 的语法扩展,而 HTML 是一种标记语言。 2. JSX 允许您在语法中包含表达式和函数,而 HTML 只允许静态文本。 3. JSX 通常用于 React 应用程序&…...

AI日报:GPT-4-Turbo正式版自带读图能力;Gemini1.5Pro开放API;SD3将于4月中旬发布;抖音宫崎骏AI特效爆火
欢迎来到【AI日报】栏目!这里是你每天探索人工智能世界的指南,每天我们为你呈现AI领域的热点内容,聚焦开发者,助你洞悉技术趋势、了解创新AI产品应用。 新鲜AI产品点击了解:AIbase - 智能匹配最适合您的AI产品和网站 ὏…...

IDEA 宝贝插件
1. Codota— 代码智能提示 Codota还包含一个网站:https://www.codota.com/code 2.Alibaba Java Code Guidelines— 阿里巴巴 Java 代码规范 3. SequenceDiagram —— 调用链路自动生成时序图 4. google-java-format —— 代码自动格式化...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
