常用十种算法滤波
十种算法滤波
- 1. 限幅滤波法(又称程序判断滤波法)
- 2. 中位值滤波法
- 3. 算术平均滤波法
- 4. 递推平均滤波法(又称滑动平均滤波法)
- 5. 中位值平均滤波法(又称防脉冲干扰平均滤波法)
- 6. 限幅平均滤波法
- 7. 一阶滞后滤波法
- 8. 加权递推平均滤波法
- 9. 消抖滤波法
- 10. 限幅消抖滤波法
1. 限幅滤波法(又称程序判断滤波法)
- 方法: 根据经验判断,确定两次采样允许的最大偏差值(设为A) 每次检测到新值时判断: 如果本次值与上次值之差<=A,则本次值有效 如果本次值与上次值之差>A,则本次值无效,放弃本次值,用上次值代替本次值
- 优点: 能有效克服因偶然因素引起的脉冲干扰
- 缺点 无法抑制那种周期性的干扰 平滑度差
2. 中位值滤波法
- 方法: 连续采样N次(N取奇数) 把N次采样值按大小排列 取中间值为本次有效值
- 优点: 能有效克服因偶然因素引起的波动干扰 对温度、液位的变化缓慢的被测参数有良好的滤波效果
- 缺点: 对流量、速度等快速变化的参数不宜
3. 算术平均滤波法
- 方法: 连续取N个采样值进行算术平均运算 N值较大时:信号平滑度较高,但灵敏度较低 N值较小时:信号平滑度较低,但灵敏度较高 N值的选取:一般流量,N=12;压力:N=4
- 优点: 适用于对一般具有随机干扰的信号进行滤波 这样信号的特点是有一个平均值,信号在某一数值范围附近上下波动
- 缺点: 对于测量速度较慢或要求数据计算速度较快的实时控制不适用 比较浪费RAM
4. 递推平均滤波法(又称滑动平均滤波法)
- 方法: 把连续取N个采样值看成一个队列 队列的长度固定为N 每次采样到一 个新数据放入队尾,并扔掉原来队首的一次数据.(先进先出原则) 把队列中的N个数据进行算术平均运算,就可获得新的滤波结果 N值的选取:流量,N=12;压力:N=4;液面,N=4 ~ 12;温度,N=1 ~ 4
- 优点: 对周期性干扰有良好的抑制作用,平滑度高 适用于高频振荡的系统
- 缺点: 灵敏度低 对偶然出现的脉冲性干扰的抑制作用较差 不易消除由于脉冲干扰所引起的采样值偏差 不适用于脉冲干扰比较严重的场合 比较浪费RAM
5. 中位值平均滤波法(又称防脉冲干扰平均滤波法)
- 方法: 相当于“中位值滤波法”+“算术平均滤波法” 连续采样N个数据,去掉一个最大值和一个最小值 然后计算N-2个数据的算术平均值 N值的选取:3~14
- 优点: 融合了两种滤波法的优点 对于偶然出现的脉冲性干扰,可消除由于脉冲干扰所引起的采样值偏差
- 缺点: 测量速度较慢,和算术平均滤波法一样 比较浪费RAM
6. 限幅平均滤波法
- 方法: 相当于“限幅滤波法”+“递推平均滤波法” 每次采样到的新数据先进行限幅处理, 再送入队列进行递推平均滤波处理
- 优点: 融合了两种滤波法的优点 对于偶然出现的脉冲性干扰,可消除由于脉冲干扰所引起的采样值偏差
- 缺点: 比较浪费RAM
7. 一阶滞后滤波法
一阶滤波,又叫一阶惯性滤波,或一阶低通滤波。是使用软件编程实现普通硬件RC低通滤波器的功能。 一阶低通滤波的算法公式为:
Y(n)=αX(n) + (1-α)Y(n-1)
式中:α=滤波系数;X(n)=本次采样值;Y(n-1)=上次滤波输出值;Y(n)=本次滤波输出值。 一阶低通滤波法采用本次采样值与上次滤波输出值进行加权,得到有效滤波值,使得输出对输入有反馈作用。
- 方法: 取a=0~1 本次滤波结果=(1-a)本次采样值+a上次滤波结果
- 优点: 对周期性干扰具有良好的抑制作用 适用于波动频率较高的场合
- 缺点: 相位滞后,灵敏度低 滞后程度取决于a值大小 不能消除滤波频率高于采样频率的1/2的干扰信号
8. 加权递推平均滤波法
- 方法: 是对递推平均滤波法的改进,即不同时刻的数据加以不同的权 通常是,越接近现时刻的数据,权取得越大。 给予新采样值的权系数越大,则灵敏度越高,但信号平滑度越低
- 优点: 适用于有较大纯滞后时间常数的对象 和采样周期较短的系统
- 缺点: 对于纯滞后时间常数较小,采样周期较长,变化缓慢的信号 不能迅速反应系统当前所受干扰的严重程度,滤波效果差
9. 消抖滤波法
- 方法: 设置一个滤波计数器 将每次采样值与当前有效值比较: 如果采样值=当前有效值,则计数器清零 如果采样值<>当前有效值,则计数器+1,并判断计数器是否>=上限N(溢出) 如果计数器溢出,则将本次值替换当前有效值,并清计数器
- 优点: 对于变化缓慢的被测参数有较好的滤波效果, 可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动
- 缺点: 对于快速变化的参数不宜 如果在计数器溢出的那一次采样到的值恰好是干扰值,则会将干扰值当作有效值导 入系统
10. 限幅消抖滤波法
- 方法: 相当于“限幅滤波法”+“消抖滤波法” 先限幅,后消抖
- 优点: 继承了“限幅”和“消抖”的优点 改进了“消抖滤波法”中的某些缺陷,避免将干扰值导入系统
- 缺点: 对于快速变化的参数不宜
相关文章:

常用十种算法滤波
十种算法滤波1. 限幅滤波法(又称程序判断滤波法)2. 中位值滤波法3. 算术平均滤波法4. 递推平均滤波法(又称滑动平均滤波法)5. 中位值平均滤波法(又称防脉冲干扰平均滤波法)6. 限幅平均滤波法7. 一阶滞后滤波…...

IO多路复用
一、概述 IO多路复用:进程同时检查多个文件描述符,以找出他们中的任何一个是否可执行IO操作。 核心:同时检查多个文件描述符,看他们是否准备好了执行IO操作。文件描述符就绪状态的转化是通过一些IO事件来触发。 二、水平触发和…...

Python中的错误是什么,Python中有哪些错误
7.1 错误(errors) 由于Python代码通常是人类编写的,那么无论代码是在解释之前还是运行之后,或多或少总会出现一些问题。 在Python代码解释时遇到的问题称为错误,通常是语法和缩进问题导致的,这些错误会导致代码无法通过解释器的解…...
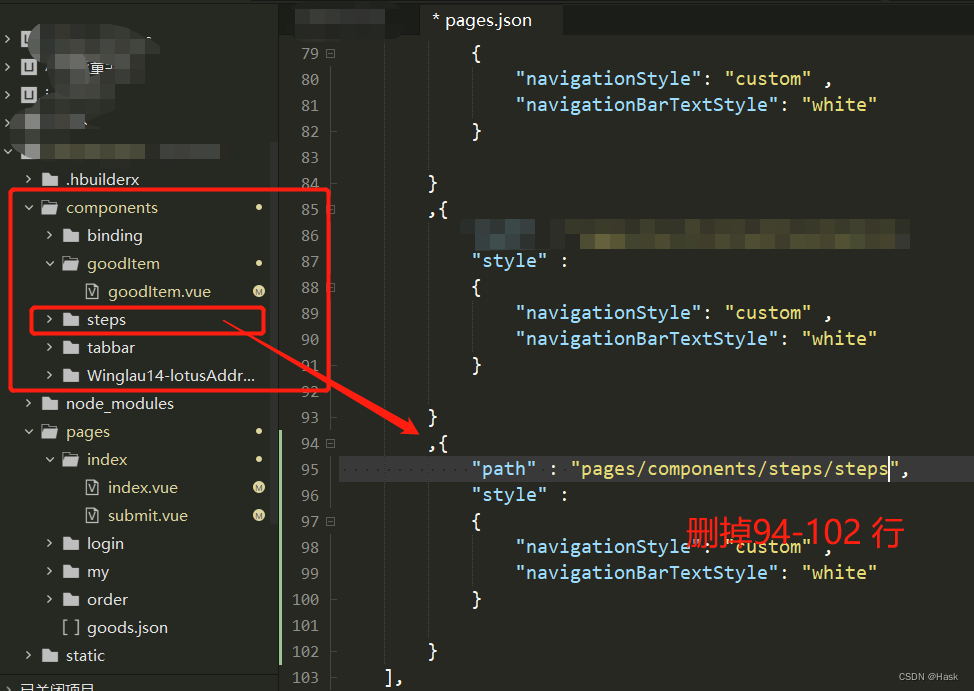
记录自己开发一款小程序中所遇到的问题(uniapp+uview)(持续更新)
每次开发小程序中,都会遇到各种各样的问题。但是有的问题已经遇到过了,但是遇到的时候还是要各种的问度娘。 特此出这篇文章,方便自己也是方便大家。 仅供参考 1. u-collapse的样式在h5中正常,但是运行到微信小程序中样式就乱了…...

华为机试 HJ43 迷宫问题
经典迷宫问题dfs 题目链接 描述 定义一个二维数组 N*M ,如 5 5 数组下所示: int maze[5][5] { 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; 它表示一个迷宫,其中的1表示墙壁,0表示可以走…...
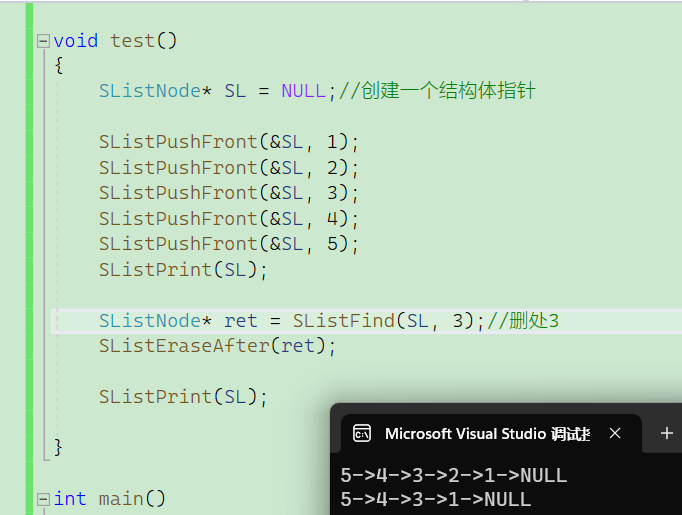
数据结构|链表
概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。单链表的形式就像一条铁链环环相扣它与顺序表最大的不同是,单链表的数据存储是在不连续的空间,存储的数据里面含有…...

计算机写论文时,怎么引用文献? - 易智编译EaseEditing
首先需要清楚哪些引用必须注明[1]: 任何直接引用都要用引号并注明来源; 任何不是自己的口头或书面的观点、解释和结论都应注明来源; 即使不用原话,但是他人的思路、概念或观点也应注明; 不要为了适合你的观点修改原…...

实验三:贪心
1.减肥的小k1 题目描述 小K没事干,他要搬砖头,为了达到较好的减肥效果,教练规定的方式很特别: 每一次,小K可以把两堆砖头合并到一起,消耗的体力等于两堆砖头的重量之和。 经过 n-1次合并后, …...
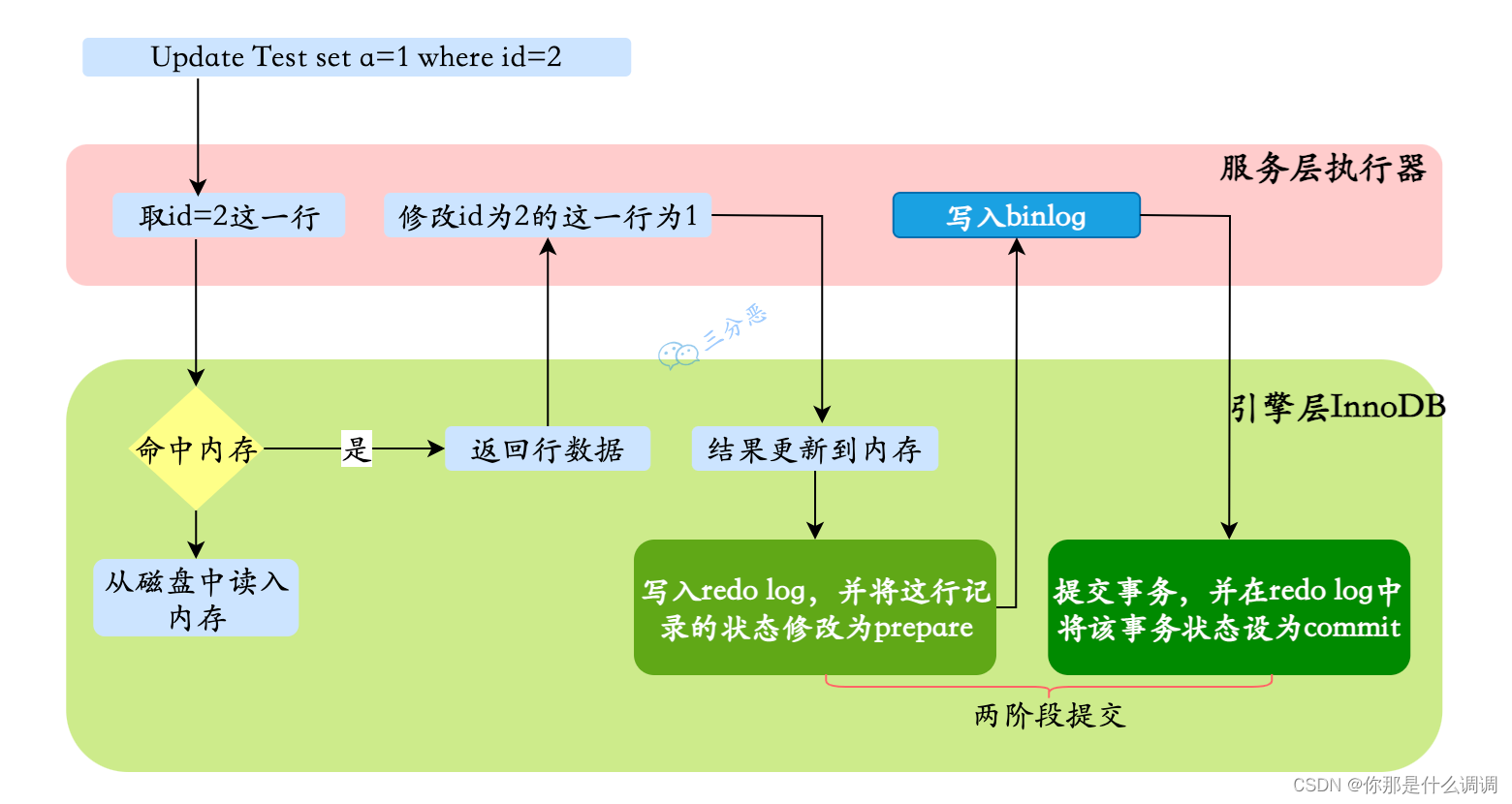
MySQL日志文件
文章目录1.MySQL中的日志文件2.bin log的作用3.redo log的作用4.bin log和redo log的区别(1)存储的内容(2)功能(3)写入时间(4)写入方式5.两阶段提交6.undo log的作用1.MySQL中的日志…...

Intel8086处理器使用NASM汇编语言实现操作系统08-关于负数的相关处理idiv/cbw/cwde/cdqu/cwd/cdq/cdo/
很多人都知道一个有符号的数,最高位是1,则表示负数,最高位是0,则表示正数,如果假设我的CPU是4位CPU,那么对于1001这个数,是表示9,还是表示-7呢???…...
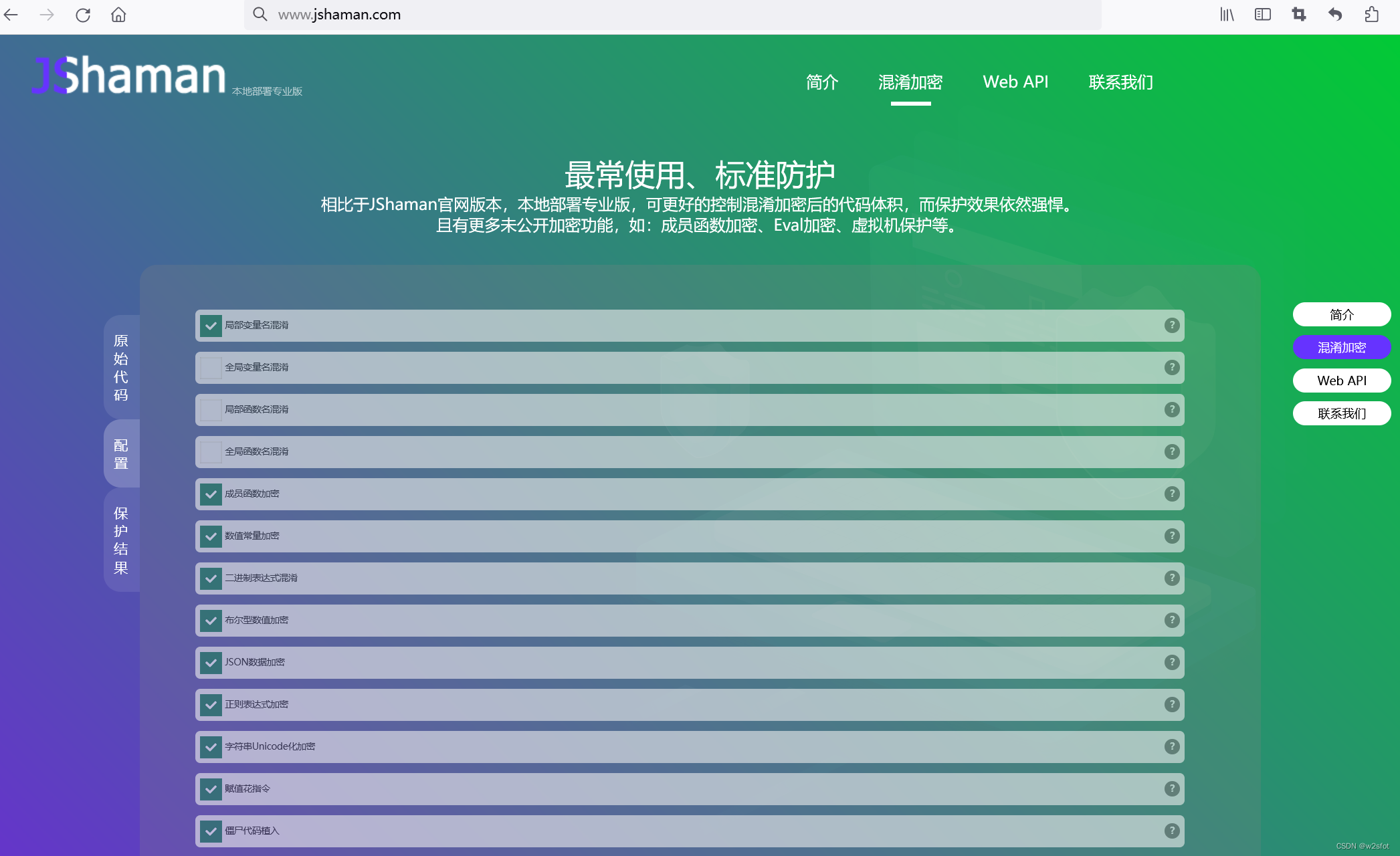
JavaScript 混淆技术
根据JShaman(JShaman是专业的JavaScript代码混淆加密网站)提供的消息,JavaScript混淆技术大体有以下几种: 变量混淆 将带有JS代码的变量名、方法名、常量名随机变为无意义的类乱码字符串,降低代码可读性,如…...

安装库报错:No CUDA runtime is found, using CUDA_HOME=‘/usr/local/cuda-11.3‘
1、报错内容 安装库时报错: No CUDA runtime is found, using CUDA_HOME/usr/local/cuda-11.32、检查 查看cuda版本和pytorch版本 python 进入python环境 import torch torch.__version__ torch.cuda.is_available()nvidia-smi 因此发现是由于该虚拟环境中CUDA与…...
CVTE前端面经(2023)
CVTE前端面经项目介绍(重点)在数据B中找到数组A对应的值,并把数组B对应的值放在数据最前面css1 定位2 外边距3 css高级应用3.1. 过渡3.2. 变形2. 浮动2.1 浮动元素特点2. 2 清除浮动3. html5语义标签4. 实现圣杯布局的两种方式4.1 定位浮动4.…...

基于EB工具的TC3xx_MCAL配置开发02_ICU模块配置
目录 1.概述2. ICU 硬件通道属性确认3. ICU通道配置3.1 添加一个Chanel3.2 IcuChannel->General配置3.3 IcuSignalMeasurement配置3.4 GtmTimerInputConfiguration配置3.5 MCU中的关联配置3.5.1 分配TIM资源给ICU使用3.5.2 设置TIM通道时钟分频系数1.概述 本篇开始我们基于…...
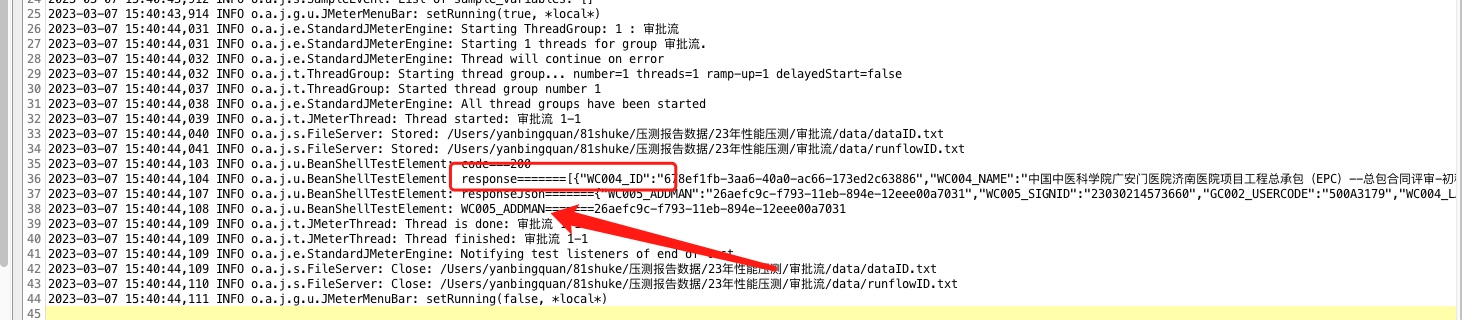
jmeter高阶系列--beanshell返回值中提取参数
1 准备环境 jmeter版本: ** ,JDK:1.8将json.jar包置于…\apache-jmeter-5.1\lib\下;否则会报:Typed variable declaration : Class: JSONObject not found in namespace的错误;处理器:Beanshel…...

面向对象
面向对象面向对象一、什么是对象二、什么是面向对象三、对象四、什么是类五、实例变量六、实例方法七、方法重载(overload)八、构造方法九、对象的创建过程十、构造方法重载十一、this关键字面向对象 一、什么是对象 万物皆对象。 二、什么是面向对象 面向对象是一种编程思想。…...

mpi4py 运行过程中出现Read -1, expected xxx, errno = 1 解决方案
目录 问题描述 代码1(串行) 代码2(并行) 代码2执行时所用指令 错误信息 解决方案 解决方案1 解决方案2 问题描述 今天正在学习使用mpi4py,在对比运行以下2个代码时疯狂报错: 代码1(串…...

PMP考前冲刺3.07 | 2023新征程,一举拿证
题目1-2:1.某公司启动了一个新型智能家电研发敏捷项目,组织上聘请了一位敏捷管理专业人士。在项目执行过程中,敏捷团队反馈用户故事包含的信息不足,无法理解需求,敏捷管理专业人应该怎么做?A.教导产品负责人…...

60条Python日常工作中的高频写法,收藏
一、 数字 1 求绝对值 绝对值或复数的模 In [1]: abs(-6) Out[1]: 62 进制转化 十进制转换为二进制: In [2]: bin(10) Out[2]: 0b1010十进制转换为八进制: In [3]: oct(9) Out[3]: 0o11十进制转换为十六进制: In [4]: hex(15) Out[4]:…...
函数笔记合集七 函数(XI)总结 python函数的函数文档、类型注释、内省详解)
(小甲鱼python)函数笔记合集七 函数(XI)总结 python函数的函数文档、类型注释、内省详解
一、基础复习 函数的基本用法 创建和调用函数 函数的形参与实参等等函数的几种参数 位置参数、关键字参数、默认参数等函数的收集参数*args **args 解包参数详解函数中参数的作用域 局部作用域 全局作用域 global语句 嵌套函数 nonlocal语句等详解函数的闭包(工厂函…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
