计算机视觉 | 基于二值图像数字矩阵的距离变换算法
Hi,大家好,我是半亩花海。本实验基于 OpenCV 实现了二值图像数字矩阵的距离变换算法。首先生成一个 480x480 的黑色背景图像(定义黑色为0,白色为1),在其中随机选择了三个白色像素点作为距离变换的原点,利用 OpenCV 中 distanceTransform 等相关函数计算并输出这些原点到其他像素点的欧氏距离、D4 距离和 D8 距离及其相应的距离矩阵,并将距离变换结果可视化。
文章目录
- 一、导入必要库
- 二、初始化输入图像和变换结果图像
- 三、根据二值图计算并输出距离矩阵
- 四、将距离矩阵转换为可视化图片
一、导入必要库
导入必要的库(cv2、numpy、matplotlib.pyplot),为后续的图像处理任务做准备。
#!/usr/bin/env python
# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt# 用来设置字体样式(黑体)以正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
二、初始化输入图像和变换结果图像
自定义 480x480 二值图,随机生成图案,初始值都是 0(黑色),并显示原始图像。
-
图像数字化:
通过传感器获得的图像是平面坐标 ( x , y ) (x,y) (x,y) 的连续函数 f ( x , y ) f(x,y) f(x,y),它的值图像对应位置的亮度。为了能够让计算机来处理,需要对图像进行采样,并且对亮度值进行量化。-
采样: 对连续函数 f ( x , y ) f(x,y) f(x,y) 进行采样,就是分别对 x x x 轴和 y y y 轴,按照固定间隔取值,得到平面坐标上的 M × N M×N M×N 个点,将其函数值作为元素生成 M M M 行 N N N 列的矩阵。
-
量化亮度值。 将 f ( x , y ) f(x,y) f(x,y) 的值转化为等价的整数值的过程称为量化,量化的级别越高,图像越细致。通常将亮度值表示为 0~255 之间的整数。
-
# 创建一个大小为 480x480 的全黑图像(确保数据类型为 8 位无符号整数)
mat = np.zeros((480, 480), dtype=np.uint8)
# 给输入图像指定三个像素点设置为白色像素,作为距离变换原点(区域块)
mat[100, 200] = 1
mat[200, 100] = 1
mat[300, 300] = 1# 显示原始图像和距离变换结果
plt.figure(figsize=(15, 5))
plt.scatter([100, 200, 300], [200, 100, 300], color='white', marker='o') # 添加三个白点表示出三个像素点的坐标
plt.imshow(mat, cmap='gray')
plt.title('原始图像', fontsize=16)
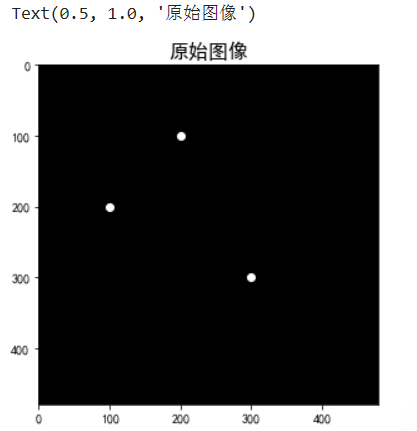
# 将输入图像中 1(白色)和 0(黑色)调换,使得原点距离为 0
mat = 1 - mat
三、根据二值图计算并输出距离矩阵
- 距离: 距离是描述图像两点像素之间的远近关系的度量,常见的度量距离有欧式距离(Euchildean distance)、城市街区距离(City block distance)、棋盘距离(Chessboard distance)。以下以两坐标点 a = ( i , j ) a = (i, j) a=(i,j) 和 b = ( k , l ) b = (k, l) b=(k,l) 的距离为例,来说明各种距离的定义方式。
(1)欧式距离 D e D_e De: 欧式距离的定义源于经典的几何学,与我们数学中所学的简单几何的两点之间的距离一致,为两个像素点坐标值的平方根。欧式距离的优点在于其定义非常地直观,是显而易见的,但缺点在于平方根的计算是非常耗时的。
D e ( a , b ) = ( ( i − k ) 2 ) + ( j − l ) 2 D_e(a, b)=\sqrt{\left((i-k)^2\right)+(j-l)^2} De(a,b)=((i−k)2)+(j−l)2
(2)城市街区距离 D 4 D_4 D4: 距离描述的是只允许像素坐标系平面中横向和纵向的移动距离,4表示在这种定义下,像素点是 4 邻接的,即每个点只与它的上、下、左、右相邻的 4 个点之间的距离为 1。
D 4 ( a , b ) = ∣ i − k ∣ + ∣ j − l ∣ D_4(a, b)=|i-k|+|j-l| D4(a,b)=∣i−k∣+∣j−l∣
(3)棋盘距离 D 8 D_8 D8: 如果允许在图像坐标系中像素点的对角线方向的移动,就可以得到棋盘距离,8 表示在这种定义下,像素点是 8 邻接的,即每个点只与它的上、下、左、右、四个对角线方向相邻的 8 个点之间的距离为 1。
D 8 ( a , b ) = max { ∣ i − k ∣ , ∣ j − l ∣ } D_8(a, b)=\max \{|i-k|,|j-l|\} D8(a,b)=max{∣i−k∣,∣j−l∣}
- 距离变换
距离变换也叫作距离函数或者斜切算法。它是距离概念的一个应用,图像处理的一些算法以距离变换为基础。距离变换描述的是图像中像素点与某个区域块的距离,区域块中的像素点值为 0,临近区域块的像素点有较小的值,离它越远值越大。
以二值图像为例,其中区域块内部的像素值为 1,其他像素值为 0。距离变换给出每个像素点到最近的区域块边界的距离,区域块内部的距离变换结果为0。输入图像如图 1 所示, D 4 D_4 D4 距离的距离变换结果如图 2 所示。

下面来讨论距离变换算法,其核心是利用两个小的局部掩膜遍历图像。第一遍利用掩模1,左上角开始,从左往右,从上往下。第二遍利用第二个掩模,右下角开始,从右往左,从下往上。掩模形状如下图所示:
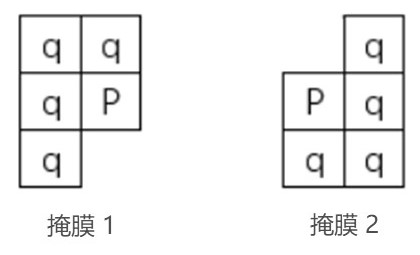
按照某种距离(如: D 4 D_4 D4 距离或 D 8 D_8 D8 距离)对大小为 M × N M×N M×N 的图像中的区域块作距离变换,算法过程如下:
(1) 建立一个大小为 M × N M×N M×N 的数组 F F F,作如下的初始化:将区域块中的元素设置为 0,其余元素设置为无穷;
(2) 利用掩模1(mask1),左上角开始,从左往右,从上往下遍历数组,将掩模中P点对应的元素的值作如下更新:
F ( P ) = min q ∈ mask1 { F ( P ) , D ( P , q ) + F ( q ) } F(P)=\min _{q \in \operatorname{mask1}}\{F(P), D(P, q)+F(q)\} F(P)=q∈mask1min{F(P),D(P,q)+F(q)}
(3) 利用掩模2(mask2),右下角开始,从右往左,从下往上遍历数组,将掩模中P点对应的元素的值作如下更新:
F ( P ) = min q ∈ mask2 { F ( P ) , D ( P , q ) + F ( q ) } F(P)=\min _{q \in \operatorname{mask2}}\{F(P), D(P, q)+F(q)\} F(P)=q∈mask2min{F(P),D(P,q)+F(q)}
最终得到的更新后的数组即为距离变换的结果。
这个算法过程在图像的边界处需要做出调整,因为在边界处,掩模不能全部覆盖图像,这时可以将掩模中没有对应元素的位置的值当作 0 来处理,即maskSize=0。
在 OpenCV 中,distanceTransform 函数是用于计算二进制图像中每个非零像素到最近零像素的距离的函数。这个函数通常用于图像处理中的形态学操作和特征提取。下面是 distanceTransform 函数的一般形式:
dist_transform = cv2.distanceTransform(src, distanceType, maskSize)
-
src: 是输入的二进制图像(该图像应该是一个 8 位单通道图像)。
-
distanceType: 是指定距离度量的类型。
-
maskSize: 是指定计算距离时使用的卷积核的大小。
# 分别利用欧式距离、D4 距离和 D8 距离作距离变换
transMatE = cv2.distanceTransform(mat, distanceType=cv2.DIST_L2, maskSize=0) # 计算欧氏距离变换
transMatD4 = cv2.distanceTransform(mat, distanceType=cv2.DIST_L1, maskSize=0) # 计算 D4 距离变换
transMatD8 = cv2.distanceTransform(mat, distanceType=cv2.DIST_C, maskSize=0) # 计算 D8 距离变换
# 输出欧式、D4 和 D8 的距离矩阵
print("欧氏距离的变换矩阵:\n", transMatE)
print("城区距离-D4的变换矩阵:\n", transMatD4)
print("棋盘距离-D8的变换矩阵:\n", transMatD8)

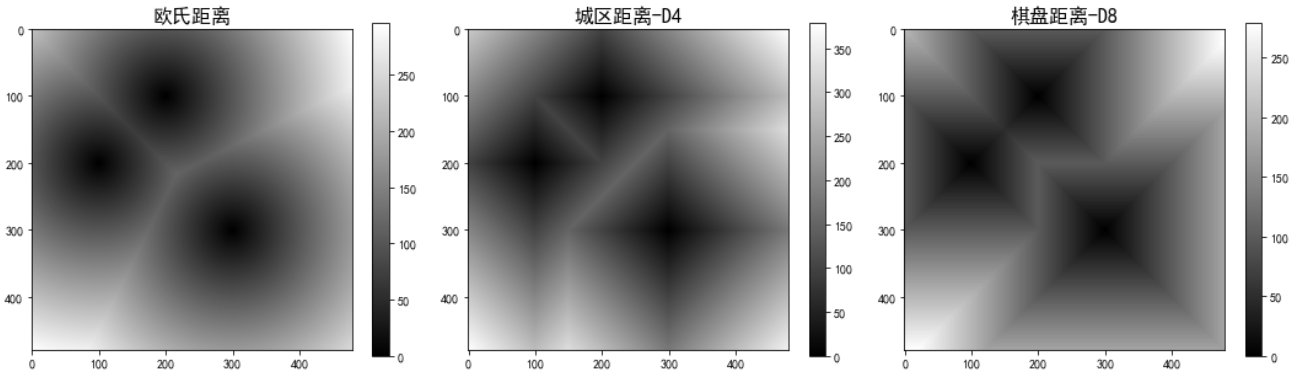
四、将距离矩阵转换为可视化图片
因为经过距离矩阵变换之后,变换结果的数据类型为 float32(32 位浮点数),而在 OpenCV 中,采用 imshow 函数显示图像时需要使用 uint8 数据类型(8 位无符号整数),使得像素值的范围是从 0~255,可以表示灰度图像中的所有可能像素值。而 Matplotlib 可以直接处理 float32 类型的图像数据,因此并不需要将图像数据类型转换为 uint8 类型。
plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)
plt.imshow(transMatE, cmap='gray')
plt.title('欧氏距离', fontsize=16)
plt.colorbar(shrink=0.8)plt.subplot(1, 3, 2)
plt.imshow(transMatD4, cmap='gray')
plt.title('城区距离-D4', fontsize=16)
plt.colorbar(shrink=0.8)plt.subplot(1, 3, 3)
plt.imshow(transMatD8, cmap='gray')
plt.title('棋盘距离-D8', fontsize=16)
plt.colorbar(shrink=0.8)plt.tight_layout()
plt.show()
相关文章:

计算机视觉 | 基于二值图像数字矩阵的距离变换算法
Hi,大家好,我是半亩花海。本实验基于 OpenCV 实现了二值图像数字矩阵的距离变换算法。首先生成一个 480x480 的黑色背景图像(定义黑色为0,白色为1),在其中随机选择了三个白色像素点作为距离变换的原点&…...

Arcgis windows webadaptor配置
注意windows下安装细节 1、电脑必须添加限定域名及dns后缀。 准备工作 a、安装webadaptor,获取jar文件 b、tomcat中部署两个jar,名字不相同,一个用server配置,一个用于portal配置 c、geoserver用来配置server d、geoscene用来配置…...

对接阿里云实时语音转文字的思路
将上述概念转化为详细代码需要一定的步骤。这里,我们将根据之前讨论的服务划分,创建一个简化的框架来模拟这个流程。注意,由于空间限制和简化目的,某些实现细节会被省略或简化,你可能需要根据实际情况进行调整。 1. 配…...
如何转行成为产品经理?
转行NPDP也是很合适的一条发展路径,之后从事新产品开发相关工作~ 一、什么是NPDP? NPDP 是产品经理国际资格认证,美国产品开发与管理协会(PDMA)发起的,是目前国际公认的唯一的新产品开发专业认证ÿ…...

SpringCloudAlibaba-整合nacos(二)
目录地址: SpringCloudAlibaba整合-CSDN博客 一、nacos服务部分 1.下载nacos,并执行数据库脚本:nacos-mysql.sql 2.修改配置文件,配置mysql 3.启动nacos ./startup.sh -m standalone 4.访问:http://127.0.0.1:884…...
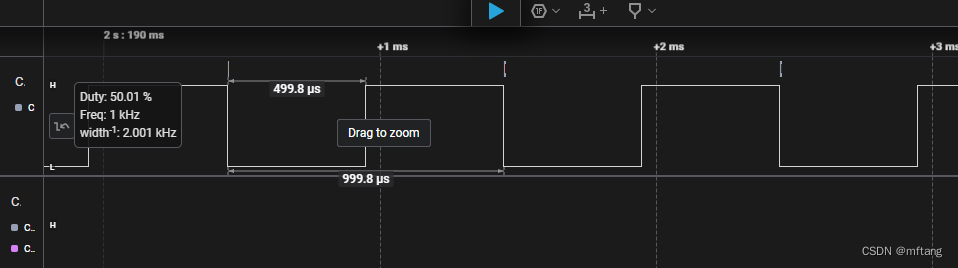
STM32H7通用定时器计数功能的使用
目录 概述 1 STM32定时器介绍 1.1 认识通用定时器 1.2 通用定时器的特征 1.3 递增计数模式 1.4 时钟选择 2 STM32Cube配置定时器时钟 2.1 配置定时器参数 2.2 配置定时器时钟 3 STM32H7定时器使用 3.1 认识定时器的数据结构 3.2 计数功能实现 4 测试案例 4.1 代码…...

信息系统项目管理师0044:IT治理方法与标准(3信息系统治理—3.1 IT治理—3.1.4 IT治理方法与标准)
点击查看专栏目录 文章目录 3.1.4 IT治理方法与标准1. ITSS中1T服务治理 3.1.4 IT治理方法与标准 考虑到IT治理对组织战略目标达成的重要性,国内外各类机构持续研究并沉淀IT治理相关的最佳实践方法、定义相关标准,这里面比较典型的是我国信息技术服务标准…...

探索Linux:在VMware虚拟机上安装Linux操作系统
探索Linux:在VMware虚拟机上安装Linux操作系统 在计算机领域,Linux操作系统以其稳定性、安全性和自由开源的特点备受青睐。通过在VMware虚拟机上安装Linux,您可以轻松体验Linux操作系统的强大功能。本文将详细介绍在VMware虚拟机上安装Linux…...

JavaScript进阶6之函数式编程与ES6ESNext规范
函数式编程 柯里化currycurrycompose示例:简化版展开写: debug示例一:示例二: 模板字符串css in js方案 箭头函数问题 生成器 generator应用场景 反射 Reflect 柯里化curry compose是curry的应用 在 lodash/fp underscore ramba …...

AcWing 1381. 阶乘
解题思路 最后一位数相乘的变化。注意:为什么不是ss%10,如果12 * 15, 12的最后一位时2, * 1530,则为3,问题是12*15180,为8,两 者不符,说明ss%10中的10要多加0. import j…...
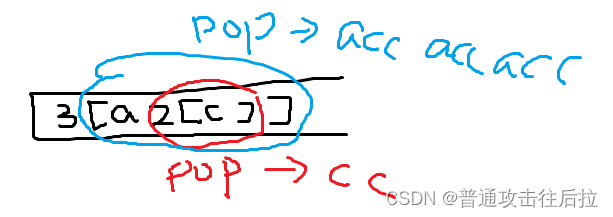
Leetcode 394. 字符串解码
心路历程: 这道题看到括号直接想到栈,五分钟新题直接秒了,一开始以为需要两个栈分别存储数字和非数字,后来发现一个栈就够了,思路如图: 这道题考察的应该是队栈这两种数据结构的转换,因为每次…...

LeetCode - 1702. 修改后的最大二进制字符串
文章目录 解析AC CODE 题目链接:LeetCode - 1702. 修改后的最大二进制字符串 解析 详细题解:贪心,简洁写法(Python/Java/C/Go/JS/Rust) 思路很牛b。 简单来说我们需要想办法将0配对,将其变为10࿰…...
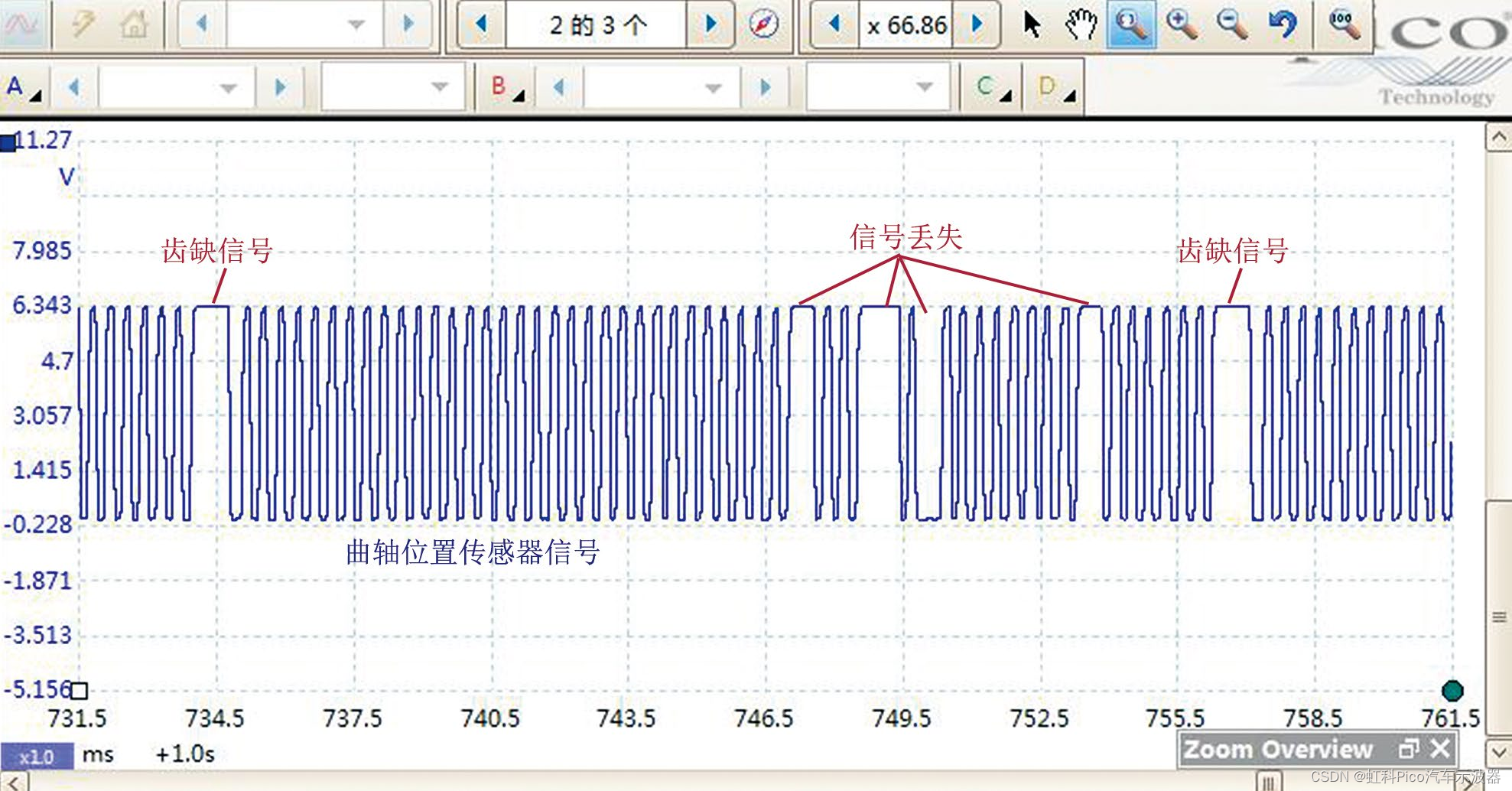
虹科Pico汽车示波器 | 免拆诊断案例 | 2011款东风悦达起亚K5车发动机偶尔起动困难
一、故障现象 一辆2011款东风悦达起亚K5车,搭载G4KD发动机,累计行驶里程约为24.5万km。车主反映,第1次起动发动机时偶尔无法起动着机,第2次能够正常起动着机,但发动机故障灯异常点亮。为此在其他维修厂维修过…...

Docker- Redis
博文目录 文章目录 说明前置命令 说明 Docker Hub Redis 数据卷数据卷印射在容器内的路径redis/data 容器内的路径说明/data数据目录/data/redis.conf配置文件 前置 在 GitHub 找一份 redis.conf 配置文件, 放到卷 redis 中, 按需修改 # bind 127.0.0.1 # 解除只允许环回地…...

Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单视频处理实战案例 之八 简单视频素描效果
Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单视频处理实战案例 之八 简单视频素描效果 目录 Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单视频处理实战案例 之八 简单视频素描效果 一、简单介绍 二、简单指定视频某片段快放效果实现原理 三、简单指定视频某…...

数据结构——线性表(链式存储结构)
语言:C语言软件:Visual Studio 2022笔记书籍:数据结构——用C语言描述如有错误,感谢指正。若有侵权请联系博主 一、线性表的逻辑结构 线性表是n个类型相同的数据元素的有限序列,对n>0,除第一元素无直接…...

面试算法-169-二叉树的中序遍历
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 示例 1: 输入:root [1,null,2,3] 输出:[1,3,2] 解 class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> resul…...

计算机视觉——引导APSF和梯度自适应卷积增强夜间雾霾图像的可见性算法与模型部署(C++/python)
摘要 在夜间雾霾场景中,可见性经常受到低光照、强烈光晕、光散射以及多色光源等多种因素的影响而降低。现有的夜间除雾方法常常难以处理光晕或低光照条件,导致视觉效果过暗或光晕效应无法被有效抑制。本文通过抑制光晕和增强低光区域来提升单张夜间雾霾…...
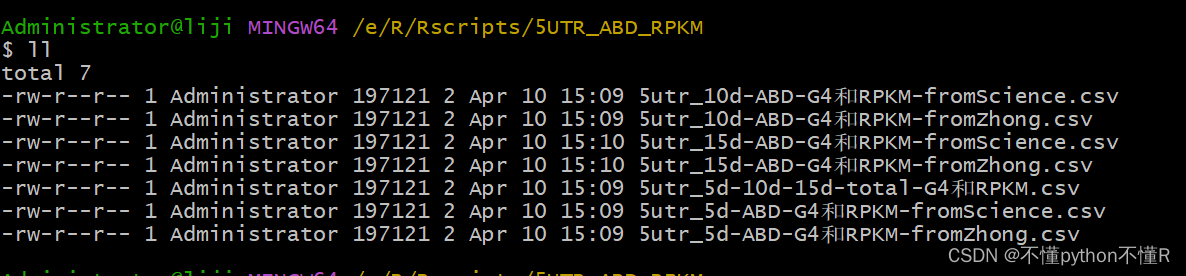
git bash用法-批量修改文件名
在win系统上安装git bash可以使用命令行模式操作,比较方便 1.原始文件名 2.代码 for file in *3utr*; do mv "$file" "$(echo "$file" | sed s/3utr/5utr/)"; done3.修改后的文件名...
分布式社交媒体:探索Web3对社交媒体的改变
在数字化时代,社交媒体已成为人们日常生活中不可或缺的一部分。然而,传统的社交媒体平台往往由中心化的机构或公司掌控,用户的数据和内容受到限制,引发了一系列的隐私和安全问题。随着区块链技术的发展,分布式社交媒体…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
