2024春算法训练4——函数与递归题解
一、前言
感觉这次的题目都很好,但是E题....(我太菜了想不到),别人的题解都上百行了,晕;
二、题解
A-[NOIP2010]数字统计_2024春算法训练4——函数与递归 (nowcoder.com)
这种题目有两种做法:1、计数dp,2、暴力(时间复杂度为0(n))
1、先讲暴力:直接枚举就行了,注意循环内要用一个变量代替i求i的数位上出现过的数字。
#include<iostream>
using namespace std;
int target=2;
int main(){int l,r;cin>>l>>r;int ans=0;for(int i=l;i<=r;i++){int s=i;while(s){int yu=s%10;if(yu==target){ans++;}s/=10;}}cout<<ans;
}2、记数类dp
这里主要是分情况讨论,假设我们要求一个数字在从一到R中出现的次数,那么就等于求这个数字在每个数出现的次数。问题就转换成了求这个数字在这个数出现的次数,进一步转换成求这个数在要求的数的每一位出现的次数之和。假设我们一直一个数abcdef,要求数字1在第三位出现的次数:
(1)前三位是0~abc-1时,数字是xxx100~xxx199,所以有abc*100种取法
(2)前三位是abc(此时讨论d)
(2.1)d<1 数字是abc000~abc099 此时有0种取法
(2.2)d=1 数字是abc100~abc1ef 此时有ef+1种取法
(2.3) d>1 数字可以取到abc100~abc199(实际范围是abc000~abcdef) 此时有100取法
如果是求区间l到r的个数的话就是用r的减去l的就可以了。特判0,但是这道题都是正整数,所以不用。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/int query(int x)
{int ret=0;while(x){x/=10;ret++;}return ret;
}int cnt(int t,int n)
{int ret=0;int wei=query(n);pre(i,1,wei){int p=pow(10,i-1);int l=n/p/10,r=n%p,d=n/p%10;/*t如果不为0,则按照一般的规则计算*/if(t)ret+=l*p;/*t如果为0,如果l为0,左边就是000..0前导0无效就不算,如果l不为0,因为t为0,所以不存在
00000...0....的情况,要从0000010...的情况开始*/if(!t&&l)ret+=(l-1)*p;/*(t||l)表示如果t为0,那么t就不能出现在最高位*/ if(d==t&&(t||l))ret+=r+1; if(d>t&&(t||l))ret+=p;}return ret;
}void solve()
{ int l,r;cin>>l>>r;cout<<cnt(2,r)-cnt(2,l-1);
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}B-素数回文_2024春算法训练4——函数与递归 (nowcoder.com)
按照题目意思求出回文数,然后写一个判断质数的函数就可以了,注意一下数据范围要开ll
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/bool isprime(ll a)
{if(a==1||a==0)return false;for(int i=2;i<=a/i;i++)if(a%i==0)return false;return true;
}bool check(string a)
{ll ret=0;pre(i,0,a.size()-1)ret=ret*10+(a[i]-'0');if(isprime(ret))return true;return false;
}void solve()
{ string a;cin>>a;pr(i,a.size()-2,0)a+=a[i];if(check(a))cout<<"prime";else cout<<"noprime";
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}C-[NOIP1999]回文数_2024春算法训练4——函数与递归 (nowcoder.com)
用一个数组求回文数,与原数组相加,最后判断是否为回文数,重复以上步骤最多30次,
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/int n;//将字符转换成数字
int tr(char ch)
{return ch<='9'?(ch-'0'):(ch+10-'A');
}//将数字转换成字符
char rt(int tt)
{return tt<=9?(tt+'0'):(tt-10+'A');
}//判断当前的数是否回文
bool check(vector<char>x)
{int l=0,r=x.size()-1;while(l<r){if(x[l]!=x[r])return false;l++;r--;}return true;
}void solve()
{ cin>>n;string ss;cin>>ss;vector<char>a;pre(i,0,ss.size()-1)a.push_back(ss[i]);//a存储数int cnt=30;bool flag=1;if(check(a)){cout<<"STEP=0";return ;}while(cnt){cnt--;int t=0;vector<char>temp,ans;//temp存储a的翻转数,ans临时存储计算结果pr(i,a.size()-1,0)temp.push_back(a[i]);//模拟不同进制的加法pr(i,a.size()-1,0){int x=tr(a[i]),y=tr(temp[i]);int tt=(t+x+y)%n;t=(x+y+t)/n;char s=rt(tt);ans.push_back(s);}if(t)ans.push_back(rt(t));/*reverse(ans.begin(),ans.end());*/ //ans如果是回文数不会对结果有影响,但是如果不是也没有影响,这一步是多余的/*pre(i,0,ans.size()-1)cout<<ans[i];cout<<endl;*/if(check(ans)){cout<<"STEP="<<30-cnt;flag=0;break;}else a=ans;}if(flag) cout<<"Impossible!";
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}D-素数中的等差数列_2024春算法训练4——函数与递归 (nowcoder.com)
先求质数,然后用一个数组将质数存储起来,(此时是有序的不用排序),然后从小到大枚举等差数列,每组等差数列最少有三个,还有可能多于三个,可以先保留最后两个然后枚举前面的。
#include<iostream>
#include<algorithm>
using namespace std;
int f[100010];
int prime(int ans){if(ans==1)return 0;if(ans==2)return 1;for(int i=2;i<=ans/i;i++){if(ans%i==0)return 0;}return 1;
}
int main(){int k=0,p=0;int l,r;scanf("%d%d",&l,&r);for(int i=l;i<=r;i++){if(prime(i))f[k++]=i;}for(int i=0;i<k-3;i++){if(f[i+2]-f[i+1]==f[i+1]-f[i]){while(f[i+2]-f[i+1]==f[i+1]-f[i]){printf("%d ",f[i]);i++;}i--;printf("%d %d\n",f[i+1],f[i+2]);i+=2;}}return 0;
}
F-日历中的数字_2024春算法训练4——函数与递归 (nowcoder.com)
每个月的话年份和月份都不会变,这两者可以直接处理,但是日的话就要一个一个的枚举。
注意小于10的月份和日是要补0的;
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/int n;int m1[]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int m2[]={0,31,29,31,30,31,30,31,31,30,31,30,31};
map<int ,int>q;bool check(int a)
{return((a%400==0)||(a%4==0&&a%100!=0))?true:false;
}void solve1(int a,int b)
{if(a<10)q[0]+=b;while(a){q[a%10]+=b;a/=10;}
}void solve2(int x)
{pre(i,1,x){if(i<10)q[0]++;int a=i;while(a){q[a%10]++;a/=10;}}
}void solve()
{ int year,month,target;while(cin>>year>>month>>target){if(check(year)){solve1(year,m2[month]);solve1(month,m2[month]);solve2(m2[month]);}else{solve1(year,m1[month]);solve1(month,m1[month]);solve2(m1[month]);}cout<<q[target]<<endl;q.clear();}
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}G-兔子的序列_2024春算法训练4——函数与递归 (nowcoder.com)
sqrt返回的是浮点数,因此如果要用其判断完全平方数就要将其转化为整形
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
}bool cmp(int a,int b)
{return a<b;
}/*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/int a[1010];
void solve()
{ int n;cin>>n;pre(i,1,n)cin>>a[i];sort(a+1,a+1+n,cmp);pr(i,n,1)if((int)sqrt(a[i])*(int)sqrt(a[i])!=a[i]){cout<<a[i];break;}
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}H-小X的多边形_2024春算法训练4——函数与递归 (nowcoder.com)
这题是一道数学题,就是将多边形分割成三角形,然后将三角形面积计算转换成向量叉乘,刚好转换成一个点和其相邻点的向量叉乘,详细证明可以看下这个大牛的博客:
计算任意多边形的面积 - tenos - 博客园 (cnblogs.com)![]() https://www.cnblogs.com/TenosDoIt/p/4047211.html代码如下:
https://www.cnblogs.com/TenosDoIt/p/4047211.html代码如下:
include<iostream>
#include<vector>
#include<cmath>
using namespace std;
int main()
{int n;cin>>n;vector<int>a,b;while(n--){int x,y;cin>>x>>y;a.push_back(x);b.push_back(y);}int s=0;for(int i=0,j=1;i<a.size();i++,j++){if(j==a.size())j=0;s+=a[i]*b[j];s-=a[j]*b[i];}int ans;if(s%2==0)ans=abs(s/2);else ans=abs(s/2)+1;cout<<ans;return 0;
}I-The Biggest Water Problem_2024春算法训练4——函数与递归 (nowcoder.com)
对于任意一个十进制数x,x=a*10^n+b*10^(n-1)+......+c*10^0;如果每次只取其位数上的数,可以发现数会越变越小,所以一定有解。按照题意模拟即可
#include<iostream>
using namespace std;
int sum=0;
void solve(int n){int s=n;sum=0;while(s){sum+=s%10;s/=10;}
}
int main(){string c;cin>>c;for(unsigned int i=0;i<c.size();i++){sum+=c[i]-'0';}while(sum>=10){solve(sum);}cout<<sum;
}J-小q的数列_2024春算法训练4——函数与递归 (nowcoder.com)
求值的话直接递归就行,但是求第一次出现的数的话要观察规律,发现是2的n次方减一

K-大吉大利,今晚吃鸡_2024春算法训练4——函数与递归 (nowcoder.com)、
此题有限制只能移动到相邻的柱子上面去我们可以将n个圆盘看成两部分,一部分是上面n-1个圆盘,另外一部分就是第n个圆盘,可以得出递归的步骤有如下几步:
如果n==1要跳两下
1、将(n-1)从A拿到C
2、将n从A拿到B;
3、将(n-1)从C拿到A
4、将n从B拿到C
5、将(n-1)从A拿到C;
当然事实上A,B,C不是固定的,固定的是A,B,C分别代表的起始柱,工具柱,目的柱,反正n被拿到目的柱后就可以忽略了,每次解决的都是n,当n-1递归到1时结束;记得特判0。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/ll ans=0;void hanoi(int x)
{if(x==1){ans+=2;return ;}hanoi(x-1);ans++;hanoi(x-1);ans++;hanoi(x-1);}void solve()
{ int x;while(scanf("%d",&x)!=EOF){ans=0;if(x)hanoi(x);cout<<ans<<endl;}
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}L-[NOIP2001]数的计算_2024春算法训练4——函数与递归 (nowcoder.com)
这题的题目描述有点问题建议去看原题。思路是如果一个数可以得到一个数那么他就可以得到这一个数的所有集合。P1028 [NOIP2001 普及组] 数的计算 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P1028
https://www.luogu.com.cn/problem/P1028
代码如下:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/int dp[N];void init()
{pre(i,1,1010)dp[i]=1;pre(i,1,1010)pre(j,1,i/2)dp[i]+=dp[j];
}void solve()
{ init();int n;cin>>n;cout<<dp[n]<<endl;
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}M-[CSP2019]格雷码(code)_2024春算法训练4——函数与递归 (nowcoder.com)
非常适合递归的一道题:又题可知每次在前面要么加1,要么加0,那么我们可以通过判断
n位数第k位数是由(n-1)位第几个数变来的,如果k在前一半,那么加一个0,否则加一个1
如果k在前一半那么它在加0之前的那个数的位置一定是在(n-1)位的第k个,因为前半段是顺序,
反之k是(n-1)位数的第(2^n-k+1)个,因为后半段是逆序。一直递归到0,1,结束即可
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/string t[2]={"0","1"};void finds(int x,ll k)
{if(x==1&&k==0){cout<<"0";return;}if(x==1&&k==1){cout<<"1";return;}if(k>=(ll)pow(2,x-1)){cout<<"1";k=(ll)pow(2,x)-k-1;finds(x-1,k);}else {cout<<"0";finds(x-1,k);}
}void solve()
{ ll n,k;cin>>n>>k;finds(n,k);
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}N-[NOIP2011]瑞士轮_2024春算法训练4——函数与递归 (nowcoder.com)
这题用sort就逃不了tle的命运,所以再看了大佬的题解后发现这题目的每一轮的排序时间复杂度可以用归并排序控制在O(n),从而逃脱tle的魔爪。
每一轮从前往后将所有人分为胜者组和败者组,因为胜者组和败者组是默认有序的,因为一开始就是按分数大小排序的,所以前一组的胜者的分数一定大于后一组的胜者的分数。然后这时候用归并排序其时间复杂度稳定是O(n)。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=1000010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} struct node
{int score,ability,h;bool operator < (const struct node &A){if(score!=A.score)return score>A.score;return h<A.h;}
}a[N],A[N],B[N];int n,r,q,cnt=1;void merge_sort()
{int i=1,j=1,k=1;while(i<=n/2&&j<=n/2){if(A[i].score>B[j].score || (A[i].score == B[j].score && A[i].h<B[j].h)){a[k].score=A[i].score;a[k].h=A[i].h;a[k++].ability=A[i++].ability;}else{a[k].score=B[j].score;a[k].h=B[j].h;a[k++].ability=B[j++].ability;}}while(i<=n/2){a[k].score=A[i].score;a[k].h=A[i].h;a[k++].ability=A[i++].ability;}while(j<=n/2){a[k].score=B[j].score;a[k].h=B[j].h;a[k++].ability=B[j++].ability;}
}void solve()
{ cin>>n>>r>>q;n*=2;pre(i,1,n)cin>>a[i].score,a[i].h=i;pre(i,1,n)cin>>a[i].ability;sort(a+1,a+1+n);for(int j=1;j<=r;j++){cnt=1;for(int i=1;i<=n;i+=2){if(a[i].ability>a[i+1].ability){A[cnt].ability=a[i].ability;B[cnt].ability=a[i+1].ability;A[cnt].score=a[i].score+1;B[cnt].score=a[i+1].score;A[cnt].h=a[i].h;B[cnt++].h=a[i+1].h;}else{A[cnt].ability=a[i+1].ability;B[cnt].ability=a[i].ability;A[cnt].score=a[i+1].score+1;B[cnt].score=a[i].score;A[cnt].h=a[i+1].h;B[cnt++].h=a[i].h;}}merge_sort();}cout<<a[q].h<<endl;
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}O-[NOIP2007]Hanoi双塔问题_2024春算法训练4——函数与递归 (nowcoder.com)
这题应该跟上面那题差不多,特点是没有条件限制,但是它的数据范围有点大。
思路参考上面,可以得出递归的步骤是:
n==1时走一步
1、将(n-1)从A拿到B
2、将(n)从A拿到C
3、将(n-1)从B拿到B
但是这题用递归会炸、、范围原因,只要改一改这其实是一道简单的dp题
递推公式如下:

考虑到结果会很大,于是我们可以采用高精度乘法:
(关于高精度可以看看这里:高精度运算-CSDN博客)
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/int dp[201][201];void init()
{dp[1][1]=1;pre(i,2,201){pre(j,1,201)dp[i][j]=dp[i-1][j]*2;int t=0;dp[i][1]++;pre(j,1,201)if(dp[i][j]>=10)dp[i][j+1]+=dp[i][j]/10,dp[i][j]%=10;}
}void solve()
{ init();int n;cin>>n;int flag=201;pre(j,1,201)dp[n][j]*=2;pre(j,1,201)if(dp[n][j]>=10)dp[n][j+1]+=dp[n][j]/10,dp[n][j]%=10;pr(i,201,1)if(dp[n][i]){flag=i;break;}pr(i,flag,1)cout<<dp[n][i];
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}P-[NOIP1998]幂次方_2024春算法训练4——函数与递归 (nowcoder.com)
这里的子任务就是如何将一个数表示成2的幂次方的问题,对于任意一个数,如果它大于等于2^n,那么他就一定可以分解成2^n+..........的形式,那么我们的一个任务就是表示2^n,然后进一步表示n,n也一定可以表示成2^m+.....的形式。(n,m均为常数)。直到其中有一个环节能够用2或者1表示,那么递归结束。至于加号,从上面的表示来看,只要递归没结束,即x不为0,就有加号。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/void gui(int x)
{pr(i,14,0){if(pow(2,i)<=x){if(i==1)cout<<2;else if(i==0)cout<<"2(0)";else {cout<<"2(";gui(i);cout<<")";}x-=pow(2,i);if(x)cout<<"+";}}}void solve()
{ int n;cin>>n;gui(n);
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}Q-[NOIP2001]一元三次方程求解_2024春算法训练4——函数与递归 (nowcoder.com)
这题有两个解法:1、暴力 2、二分,3、盛金公式。
1、暴力感觉有点勉强(能做出来就是win)直接枚举所有的可能解,注意要时间复杂度和eps的取值
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/double a,b,c,d;double f(double x){double ret=a*x*x*x+b*x*x+c*x+d;return ret;
}
double eps=1e-2;void solve()
{ cin>>a>>b>>c>>d;int cnt=0;double i=-100.0;while(cnt<3&&i<=100){if(fabs(f(i))<eps){printf("%.2f ",i);cnt++;i+=1;} i+=0.001;}
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}2、二分:题目说如果两端点值异号那么区间至少有一个解,而且两个解的距离大于等于1,所以我们对每个长度为一两端点异号的区间进行二分的话,不考虑两端点都是解的情况下,一定可以二分出一个正解。同时要特判端点值,因为区间为闭区间。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/double a,b,c,d;double f(double x){return a*x*x*x+b*x*x+c*x+d;
}
double eps=1e-2;void solve()
{ scanf("%lf %lf %lf %lf",&a,&b,&c,&d);int cnt=0;pre(i,-100,100){double y1=f(i*1.0);double y2=f((i+1)*1.0);if(!y1){ cnt++;printf("%.2lf ",i*1.0);}if(y1*y2<0){double l=i,r=i+1;while(r-l>=0.001){ double mid=(l+r)/2;if(f(mid)*f(l)<=0)r=mid;else l=mid;}printf("%.2lf ",l);cnt++;}if(cnt==3)break;}
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}3、盛金公式,建议自行搜索。
R-[NOIP2002]过河卒_2024春算法训练4——函数与递归 (nowcoder.com)
这题看起来好有感觉,直接用dp写了。我们可以先忽略马这个元素,如果只用求路径数的话,那么
对于所有第一排和第一列的格子,显然都只有一种走法,然后对于其他格子的路径总数等于其上面格子的路径总数加上左边的格子的路径总数。
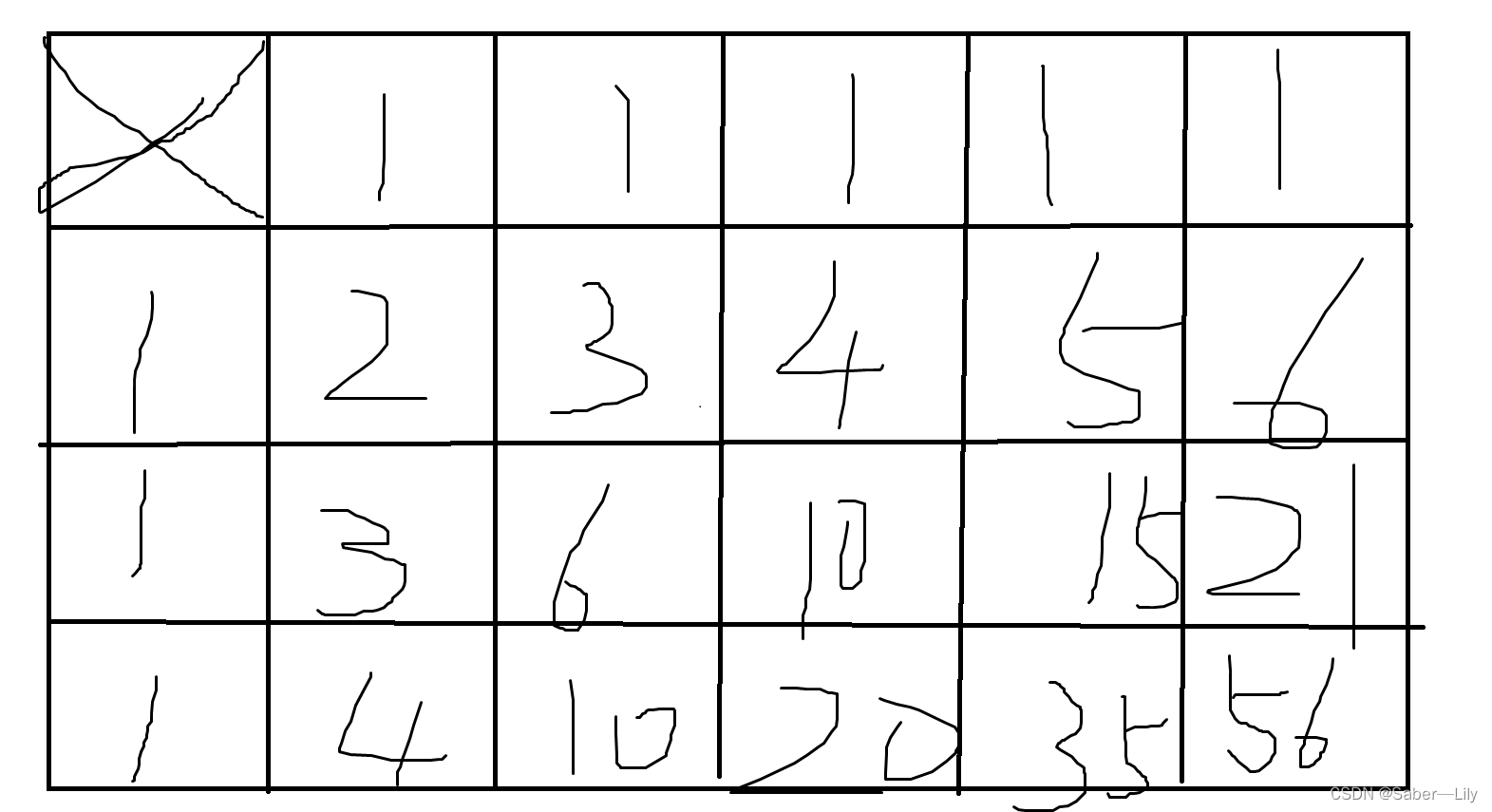
加入马之后要考虑其影响,1、如果马可以出现在第一行或者第一列那么第一行或者第一列在那个点后面的格子就不可能到达了;2、如果上面或者左边马可以到达那么那个点的路径数一定为0,
代码如下:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>
#include<map>
#define pre(i,l,r)for(int i=l;i<=r;i++)
#define pr(i,r,l)for(int i=r;i>=l;i--)
using namespace std;
typedef long long ll;
typedef pair<int ,int>pii;const int N=300010;ll gcd(ll x,ll y)
{return !y?x:gcd(y,x%y);
} /*struct node
{char ch;int num;bool operator < (const struct node &A){return num<A.num;}
}a[N];*/
int dx[]={2,2,1,1,-2,-2,-1,-1},dy[]={1,-1,2,-2,1,-1,2,-2};
ll ans[21][21];void solve()
{ int n,m,a,b;cin>>n>>m>>a>>b;ans[a][b]=-1;pre(i,0,7){int x=a+dx[i],y=b+dy[i];if(x>=0&&x<=n&&y>=0&&y<=m)ans[x][y]=-1;}pre(i,0,n){if(ans[i][0]!=-1)ans[i][0]=1;else break;}pre(i,0,m){if(ans[0][i]!=-1)ans[0][i]=1;else break;}pre(i,1,n){pre(j,1,m){if(ans[i][j]==-1)continue;if(ans[i-1][j]!=-1)ans[i][j]+=ans[i-1][j];if(ans[i][j-1]!=-1)ans[i][j]+=ans[i][j-1];}}cout<<ans[n][m];
} int main()
{int _;//cin>>_;_=1;while(_--){solve();}return 0;
}相关文章:

2024春算法训练4——函数与递归题解
一、前言 感觉这次的题目都很好,但是E题....(我太菜了想不到),别人的题解都上百行了,晕; 二、题解 A-[NOIP2010]数字统计_2024春算法训练4——函数与递归 (nowcoder.com) 这种题目有两种做法:…...

【C++】C++知识点复习
牛客cpp:牛客网在线编程 2024年4月10日:BC1—>BC8 BC4:浮点数精度保留 问题:不加入fixed输入0.359813,最后得到0.36,并不是强制保留0.360。这种写法会保留小数点后三位精度,但是最后输出会省略掉最后…...

SpringBoot+Vue,轻松实现网页版人脸登录与精准识别
目录 1、技术介绍 2、技术原理 2.1、人脸检测 ①参考模板法 ②人脸规则法 2.2、人脸跟踪 2.3、人脸比对 ①特征向量法 ②面纹模板法 识别过程 案例 一、springboot后端项目 1,拉取项目后,导入相关依赖jar包 2,执行sql文件夹下面…...

深入浅出 -- 系统架构之垂直架构
当业务复杂度增加、访问量逐渐增大出现高并发时,单体架构无法满足需求,可以根据业务功能对系统进行拆分,以提高访问效率。 垂直架构介绍 1.垂直架构一般是因为单体架构太过于庞大而进行的拆分,拆分后各个系统应满足独立运行互相不…...
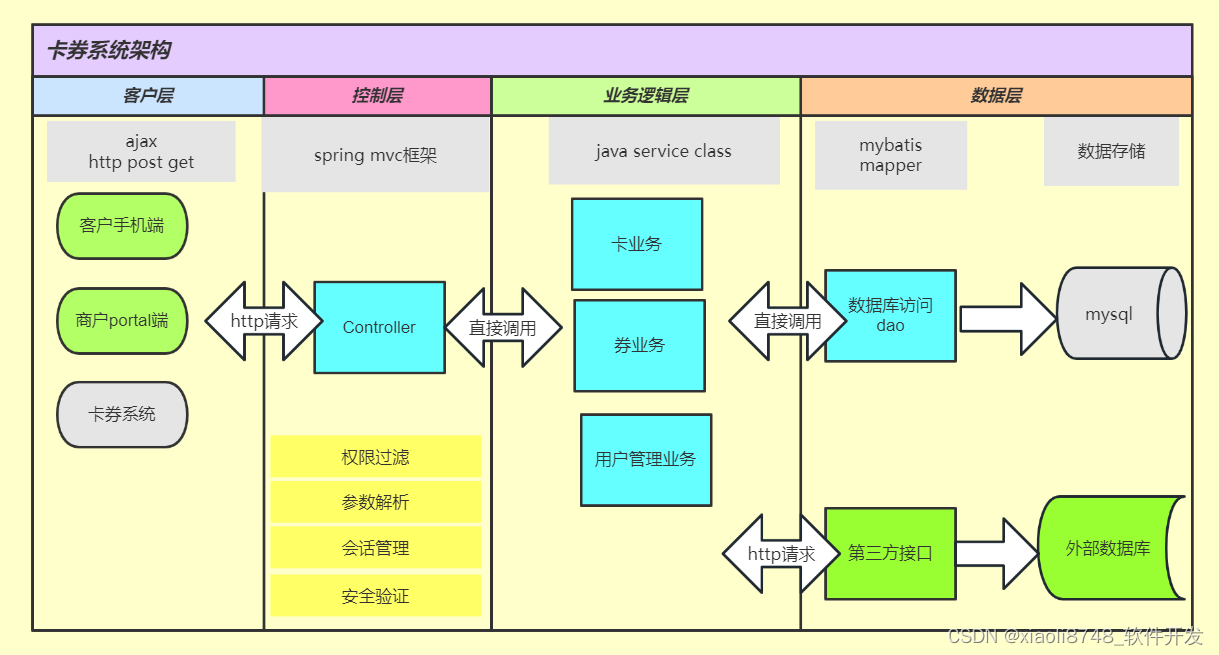
深入浅出 -- 系统架构之微服务架构选型参考图
技术选型架构图 是一个用于展示项目中所采用的各种技术和组件之间关系的图表。 它通常包括以下几个部分: 1. 项目名称和描述:简要介绍项目的背景和目标。 2. 技术栈:列出项目中使用的主要技术和工具,如编程语言、框架、数据库…...

Java 使用 ant.jar 执行 SQL 脚本文件
Java 使用 ant.jar 执行 SQL 脚本文件,很简单。 在 pom.xml 中导入 ant 依赖 <dependency><groupId>org.apache.ant</groupId><artifactId>ant</artifactId><version>1.10.11</version> </dependency>sql 脚本文件…...

【随笔】Git 高级篇 -- 快速定位分支 ^|~(二十三)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...

git环境切换
文章目录 一. 操作步骤:1.查看全局设置3.Git 切换本地git设置4.切换仓库并推送 一. 操作步骤: 1.查看全局设置 $ Git config --global --list credential.https://codeup.aliyun.com.providergeneric user.namebiejiahao user.emailxxxxxxxxqq.com3.Gi…...

hyperf websocket
composer require hyperf/websocket-server 配置 Server 修改 config/autoload/server.php,增加以下配置。 <?phpreturn [servers > [[name > ws,type > Server::SERVER_WEBSOCKET,host > 0.0.0.0,port > 9502,sock_type > SWOOLE_SOCK_TCP…...

用Echarts词云数据可视化热词表白
目录 1、使用前准备 2、准备工作 3、盒子搭建 4、整体展现 1、使用前准备 找到表白对象(重中之重!),不要一见钟情(个人觉得:一见钟情属于见色起意!),因为数据可视化需…...

VUE 实现路由的基本原理
路由 基本概念 在前端技术早期,所有页面的跳转通过更改url,浏览器页面刷新获取新的页面内容,这种粗糙的交互方式,一直等待优化。 后来,改变发生了——Ajax 出现了,它允许人们在不刷新页面的情况下发起请求࿰…...

Android 11 添加系统属性
在初识Android 属性一文中提到,系统会默认加载以下文件 /system/etc/prop.default /system/build.prop /system_ext/build.prop /vendor/default.prop /vendor/build.prop /odm/etc/build.prop /product/build.prop /factory/factory.prop要弄清楚我们应该在哪里添…...

docker 创建容器过程
结合下图,本文讨论docker 创建容器过程: START└── [用户通过Docker Client发出指令]└── (1) docker run 或 docker create 命令├── (2) Docker Client与Docker Daemon建立通信连接└── (3) Docker Daemon接收到创建容器请求├── (4) 检查…...

OSI七层网络攻击行为及防范手段
2020年3月3日,360安全大脑披露美国中央情报局攻击组织(APT-C-39)对我国大型互联网公司、政府部门及相关企业进行长达11年的网络攻击渗透,该组织所使用的网络武器和CIA“Vault7”项目中的网络武器完全吻合。如今随着互联网技术的蓬…...
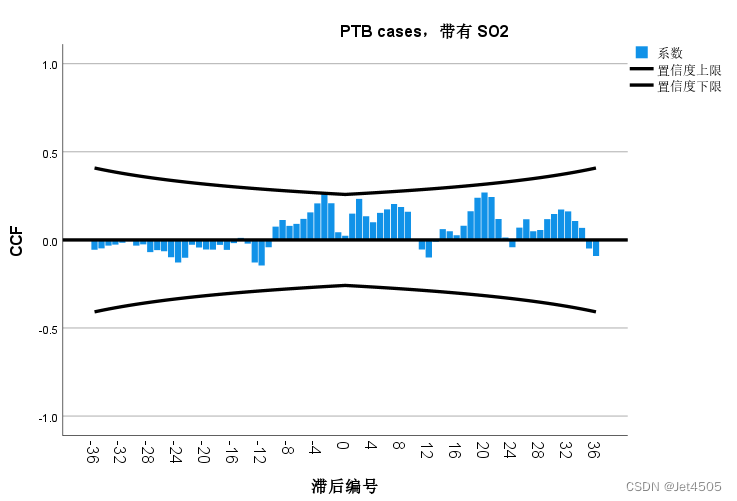
第100+5步 ChatGPT文献复现:ARIMAX预测肺结核 vol. 5
基于WIN10的64位系统演示 一、写在前面 我们继续往下看,首先例行回顾文章: 《PLoS One》杂志的2023年一篇题目为《A comparative study of three models to analyze the impact of air pollutants on the number of pulmonary tuberculosis cases in …...

论文| Convolutional Neural Network-based Place Recognition - 2014
2014-Convolutional Neural Network-based Place Recognition...

基于微信小程序的自习室预约系统的设计与实现
个人介绍 hello hello~ ,这里是 code袁~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 🦁作者简介:一名喜欢分享和记录学习的…...
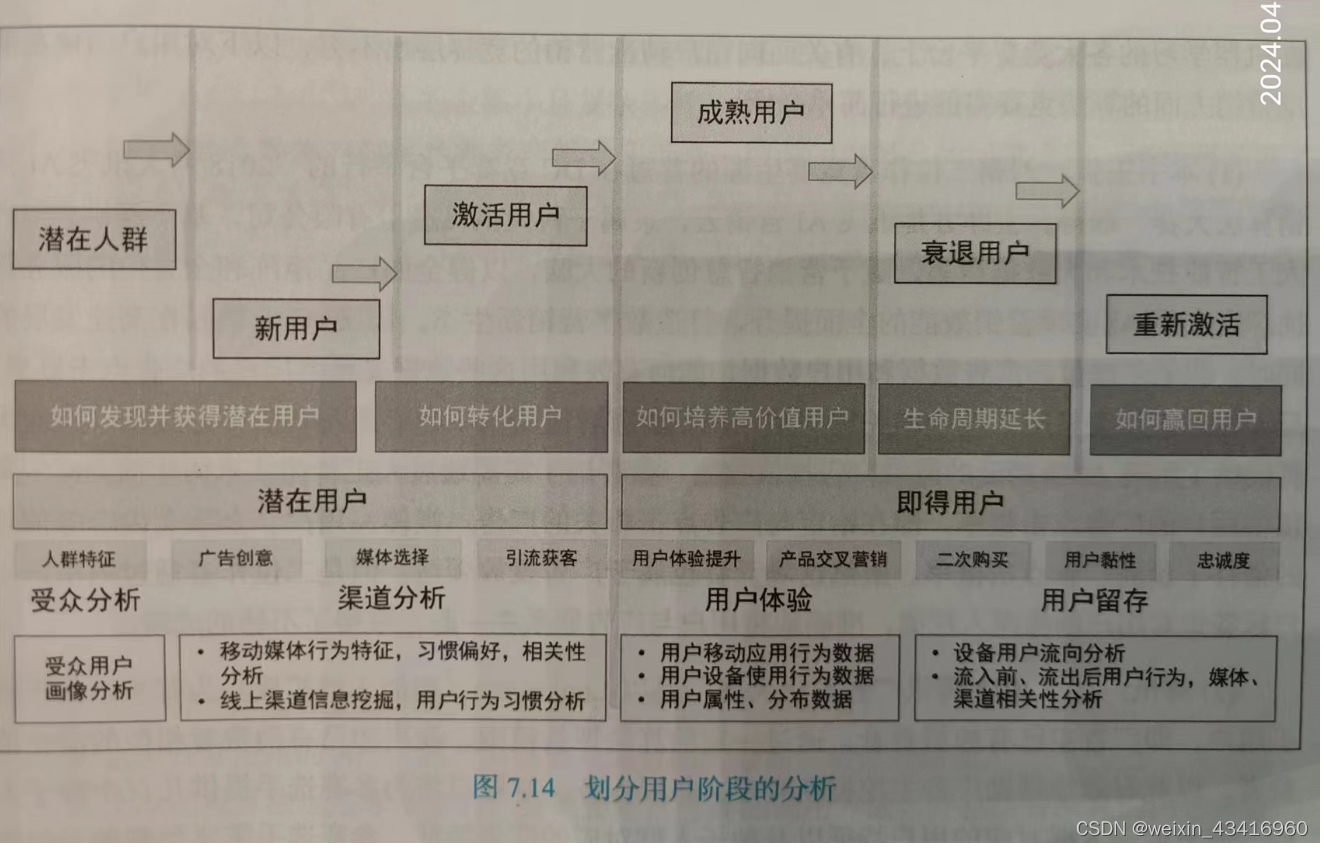
【机器学习】《机器学习算法竞赛实战》第7章用户画像
文章目录 第7章 用户画像7.1 什么是用户画像7.2 标签系统7.2.1 标签分类方式7.2.2 多渠道获取标签7.2.3 标签体系框架 7.3 用户画像数据特征7.3.1 常见的数据形式7.3.2 文本挖掘算法7.3.3 神奇的嵌入表示7.3.4 相似度计算方法 7.4 用户画像的应用7.4.1 用户分析7.4.2 精准营销7…...

vue3新手笔记
setup(){}函数,是启动页面后,自动执行的一个函数。所有数据(常量、变量)、函数等等,都要return 出去。 ref函数(可用于基本数据类型,也可以用于复杂数据类型):让页面上的…...
互联网大厂ssp面经之路:计算机网络part1
1. 计算机网络的组成部分有哪些? a. 硬件设备:计算机网络由各种硬件设备组成,包括计算机、服务器、路由器、交换机、网卡等。这些设备通过物理连接(如网线、光纤)相互连接。 b. 协议:计算机网络中的通信需…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
